Originating author is Christiane Rousseau.
Originating author is Christiane Rousseau.
In this vignette, we will show how we start from a small game to discover one of the most powerful theorems of mathematics, namely the Banach fixed point theorem. This theorem has fantastic applications inside and outside mathematics. In Section 3 we will discuss the fascinating application to image compression.
But, let us start with our game and look at the famous lid of a box of The Laughing Cow.
The right earring of the Cow is again a Laughing Cow. To each point of the lid, we associate the corresponding point on the right earring. This is of course a function from the lid to itself, which we will call ![]() . For instance, to the tip of the chin of the cow we associate the tip of the chin of the small cow on the right earring. To the center of the right eye of the cow we associate the center of the right eye of the small cow on the right earring, etc. Now here is the quiz: is there is a point that is sent to itself by this process? Such a point, if it exists, will be called a fixed point. If a fixed point exists, then it is not any of the points we have listed above. Also, if a fixed point exists, then it should lie in the right earring. But this right earring is sent to the right earring of the small cow, etc. Visually, we see that these nested right earrings seem to converge to a point, which we call
. For instance, to the tip of the chin of the cow we associate the tip of the chin of the small cow on the right earring. To the center of the right eye of the cow we associate the center of the right eye of the small cow on the right earring, etc. Now here is the quiz: is there is a point that is sent to itself by this process? Such a point, if it exists, will be called a fixed point. If a fixed point exists, then it is not any of the points we have listed above. Also, if a fixed point exists, then it should lie in the right earring. But this right earring is sent to the right earring of the small cow, etc. Visually, we see that these nested right earrings seem to converge to a point, which we call ![]() , and
, and ![]() is a candidate for our solution.
is a candidate for our solution.
Now, let us start with any point, for instance the tip of the chin and call it ![]() . Then
. Then ![]() is sent to
is sent to ![]() , which is the tip of the chin of the small cow on the right earring. Then
, which is the tip of the chin of the small cow on the right earring. Then ![]() is sent to
is sent to ![]() , which is the tip of the chin of the cow appearing on the right earring of the small cow. Etc. We remark three things:
, which is the tip of the chin of the cow appearing on the right earring of the small cow. Etc. We remark three things:
- We could continue the process an infinite number of times and generate a sequence
 , where
, where 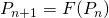 .
.
- Visually, only a finite number of points of the sequence look distinct, and all the others cannot be distinguished. Of course, we can zoom and we will see more points. But, whatever a zoom we choose, we will still distinguish only a finite number of points and the others cannot be distinguished.
- This sequence seems to converge to the same point
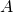 as before.
as before.
Had we taken another point ![]() and constructed the sequence
and constructed the sequence ![]() , where
, where ![]() , we would have seen that the sequence
, we would have seen that the sequence ![]() would have seemed to converge to the same point
would have seemed to converge to the same point ![]() . In fact, we can remark that this follows from the fact that the singleton
. In fact, we can remark that this follows from the fact that the singleton ![]() is the intersection of the nested right earrings whose diameter tends to
is the intersection of the nested right earrings whose diameter tends to ![]() .
.
What will Banach fixed point theorem tell us? It will tell us that indeed the function ![]() has a unique fixed point, i.e. there exists a unique point
has a unique fixed point, i.e. there exists a unique point ![]() of the plane such that
of the plane such that ![]() . Moreover, it will also assert that if we take any point
. Moreover, it will also assert that if we take any point ![]() and we construct the sequence
and we construct the sequence ![]() , where
, where ![]() , then the sequence
, then the sequence ![]() will converge to
will converge to ![]() .
.
But why? Would have that occurred for any function ![]() ? Of course not. For instance, a translation on the plane has no fixed point. And the map
? Of course not. For instance, a translation on the plane has no fixed point. And the map ![]() has the two fixed points
has the two fixed points ![]() . The map
. The map ![]() of our game has a special property. It is a contraction. Indeed, the image is much smaller than the domain. If two points
of our game has a special property. It is a contraction. Indeed, the image is much smaller than the domain. If two points ![]() and
and ![]() are some distance apart, then their images
are some distance apart, then their images ![]() and
and ![]() are closer one to the other than
are closer one to the other than ![]() and
and ![]() are. This statement makes sense because in
are. This statement makes sense because in ![]() we can measure the distance between two elements. This is because
we can measure the distance between two elements. This is because ![]() is a metric space. It is the property that
is a metric space. It is the property that ![]() is a contraction which guarantees that, when we construct the sequence
is a contraction which guarantees that, when we construct the sequence ![]() , then, whatever the threshold of precision we take, (whether we look at the sequence from far, or close to it, or through a microscope, or through an electronic microscope), then after some
, then, whatever the threshold of precision we take, (whether we look at the sequence from far, or close to it, or through a microscope, or through an electronic microscope), then after some ![]() which depends on our threshold, all elements
which depends on our threshold, all elements ![]() ,
, ![]() , of the sequence become indistinguishable. Two elements are distinguishable if the distance between them is above a certain threshold. We will recall in the next section that a sequence having this property is called a Cauchy sequence. In
, of the sequence become indistinguishable. Two elements are distinguishable if the distance between them is above a certain threshold. We will recall in the next section that a sequence having this property is called a Cauchy sequence. In ![]() , we have the property that every Cauchy sequence has a limit. We say that
, we have the property that every Cauchy sequence has a limit. We say that ![]() is a complete metric space.
is a complete metric space.
1. The Banach fixed point theorem
We now have all the ingredients for the general case and we can state the theorem.
Theorem (Banach fixed point theorem). Let ![]() be a complete metric space in which the distance between two points
be a complete metric space in which the distance between two points ![]() and
and ![]() is denoted
is denoted ![]() . And let
. And let ![]() be a contraction, i.e. there exists
be a contraction, i.e. there exists ![]() such that for all
such that for all ![]() , then
, then
![]()
Then ![]() has a unique fixed point, i.e. there exists a unique
has a unique fixed point, i.e. there exists a unique ![]() such that
such that ![]() .
.
We will define all terms appearing in this statement. This part is more formal and can be skipped if you prefer to concentrate on the fascinating applications.
We know what is the distance of two points ![]() and
and ![]() in
in ![]() . How do we generalize to a set
. How do we generalize to a set ![]() ?
?
Definition. A distance on a set ![]() is a function
is a function ![]() satisfying
satisfying
- For all
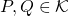 ,
, 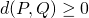 ;
;
-
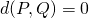 if and only if
if and only if 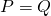 ;
;
- For all
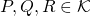 ,
, 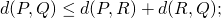 (triangular inequality.)
(triangular inequality.)
We know that these properties are satisfied for the usual Euclidian distance in ![]() .
.
We now recall the definition of Cauchy sequence, which is the formalization of the concept of a sequence for which, whatever threshold of precision we take, after a finite number of elements, all other elements become indistinguishable. We also recall the definition of convergent sequence.
Definition.
- A sequence
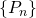 of elements of a metric space
of elements of a metric space 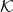 is a Cauchy sequence if for all
is a Cauchy sequence if for all 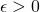 , there exists
, there exists 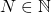 such that for all
such that for all 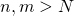 , then
, then
![Rendered by QuickLaTeX.com \[d(P_n,P_m)<\epsilon.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-1c97f4794c43d7a0ea39241b9d7b70f0_l3.png)
- A sequence
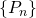 of elements of a metric space
of elements of a metric space 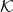 converges to a limit
converges to a limit 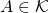 if for all
if for all 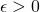 , there exists
, there exists 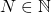 such that for all
such that for all 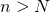 , then
, then
![Rendered by QuickLaTeX.com \[d(P_n,A)<\epsilon.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-15d19b7399d98032c767b201bb2322a3_l3.png)
Definition. A metric space ![]() is a complete metric space if any Cauchy sequence
is a complete metric space if any Cauchy sequence ![]() of elements of
of elements of ![]() converges to an element
converges to an element ![]() of
of ![]() .
.
How do we prove Banach fixed point theorem? The uniqueness of the fixed point is easy. Indeed, suppose that ![]() and
and ![]() are two fixed points. Then,
are two fixed points. Then, ![]() and
and ![]() . Moreover, since
. Moreover, since ![]() is a contraction, then
is a contraction, then
![]()
and hence, ![]() . The only solution is
. The only solution is ![]() , which yields
, which yields ![]() .
.
As for the existence, the idea of the proof is also simple: we had already found it in our game with the Laughing Cow! We take any point ![]() and we construct (as before) the sequence
and we construct (as before) the sequence ![]() , where
, where ![]() . Then, this sequence is a Cauchy sequence and its limit is a fixed point. (Of course, showing these two assertions require some work, but we will skip the technical details. What is important is that the proof is the same in the general case of a complicated complete metric space as in the simple case
. Then, this sequence is a Cauchy sequence and its limit is a fixed point. (Of course, showing these two assertions require some work, but we will skip the technical details. What is important is that the proof is the same in the general case of a complicated complete metric space as in the simple case ![]() .)
.)
The idea of the proof is not only simple and intuitive, but also very powerful. It provides us with a way of numerically constructing the fixed point ![]() . This explains that the many applications of this theorem can be found both on the theoretical side and on the applied side.
. This explains that the many applications of this theorem can be found both on the theoretical side and on the applied side.
2. The applications in analysis
One of the very important theoretical application of Banach fixed point theorem is the proof of existence and uniqueness of solutions of differential equations sufficiently regular. In this application, the complete metric space ![]() is a set of functions, and the map
is a set of functions, and the map ![]() transforms a function into another function (we often say that
transforms a function into another function (we often say that ![]() is an operator). The trick is to show that a solution of the differential equation, if its exists, is a fixed point of the operator
is an operator). The trick is to show that a solution of the differential equation, if its exists, is a fixed point of the operator ![]() .
.
You may have studied simple differential equations and have learnt tricks to find formulas for the solutions. Well, these differential equations are the exception and, for most differential equations, no formula exists for the solution. Hence, the importance of a theorem asserting the existence of a solution. You should not be surprised that no formula can be given for the solutions of most differential equations. Indeed, consider the simple differential equation
![]()
Its solution is given by
![]()
You may remember being told in your probability or statistics course that there exists no formula for the primitive of the function ![]() , hence explaining why we need to work with tables when we study the normal law.
, hence explaining why we need to work with tables when we study the normal law.
3. Application to image compression
The best way to store an image in memory is to store the color of each pixel. There are two problems with this method:
- It requires an enormous quantity of memory.
- If we try to enlarge the image, for instance for using it in a large poster, then the pixels will become larger squares and we will be missing information on how to fill the details in these squares.
What is the principle of image compression? It is to encode less information than the original image, but to do it in a clever way, so that the eye cannot see that the image observed is deteriorated. Internet has increased the need for good image compression. Indeed, images slow down navigation on the web quite significantly.  So, for internet navigation, it is good to have images encoded in files as small as possible. When you look at the image on your computer screen you cannot see that it has been deteriorated. But, if you try to enlarge it or to use it for a poster, then you immediately see that the quality is poor.
So, for internet navigation, it is good to have images encoded in files as small as possible. When you look at the image on your computer screen you cannot see that it has been deteriorated. But, if you try to enlarge it or to use it for a poster, then you immediately see that the quality is poor.
There are several principles of image compression and one of the most familiar is JPEG, which has become the standard for digital photos. The encoding of an image in JPEG format is also a mathematical algorithm.
 In this vignette, we will concentrate on another method, which has remained more experimental. This method, introduced by Barnsley, has been called iterated function systems. The underlying idea of the method is to approximate an image by geometric objects. To have sufficiently many objects available, we will not limit ourselves to the usual geometric objects which are lines and smooth curves, but allow complicated fractal objects like the fern and the Sierpiński carpet (see figures on the left).
In this vignette, we will concentrate on another method, which has remained more experimental. This method, introduced by Barnsley, has been called iterated function systems. The underlying idea of the method is to approximate an image by geometric objects. To have sufficiently many objects available, we will not limit ourselves to the usual geometric objects which are lines and smooth curves, but allow complicated fractal objects like the fern and the Sierpiński carpet (see figures on the left).
 We will explain the idea of the compression process on the Sierpiński carpet on the left. It looks a priori a complicated object. How to store it in computer memory, in an economical way? The best is to store a program to reconstruct it when needed.
We will explain the idea of the compression process on the Sierpiński carpet on the left. It looks a priori a complicated object. How to store it in computer memory, in an economical way? The best is to store a program to reconstruct it when needed.
And to build this program, we need to understand what characterizes this geometric object. Let us observe our Sierpiński carpet: it is the union of three Sierpiński carpets (i.e. 3 copies of itself), that are half its size (in width and height). Indeed, starting from the Sierpiński carpet, we can construct a second one with the following procedure:
- We shrink the Sierpiński carpet to its half size from the lower left vertex.
- We make a second copy of this half Sierpiński carpet and glue it on the right.
- We make a third copy of this half Sierpiński carpet and glue it on the top.
The second figure we have built is identical to our initial Sierpiński carpet. So the Sierpiński carpet is the fixed point for this process.
Let us now put that in mathematical terms. Note that the length of the base of the Sierpiński carpet is equal to its height. Hence, we can take axes with the origin at the lower left corner of the Sierpiński carpet, and units so that the base and height have both length 1. We also take the following affine transformations defined on ![]() :
:
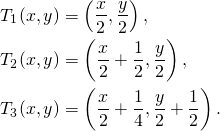
If ![]() is the Sierpiński carpet, then we have
is the Sierpiński carpet, then we have
![]()
Are there other subsets ![]() of the plane which have the same property, namely
of the plane which have the same property, namely
(1) ![]()
We will experiment and see that there are none! So we have characterized our Sierpiński carpet as the only subset ![]() of the plane such that (1) is satisfied. What have we done? We have constructed a function which, to a subset
of the plane such that (1) is satisfied. What have we done? We have constructed a function which, to a subset ![]() of the plane associates the subset
of the plane associates the subset ![]() . Let us call this function
. Let us call this function ![]() . It is defined by
. It is defined by
(2) ![]()
and we have observed that ![]() , i.e.
, i.e. ![]() is a fixed point of this function.
is a fixed point of this function.
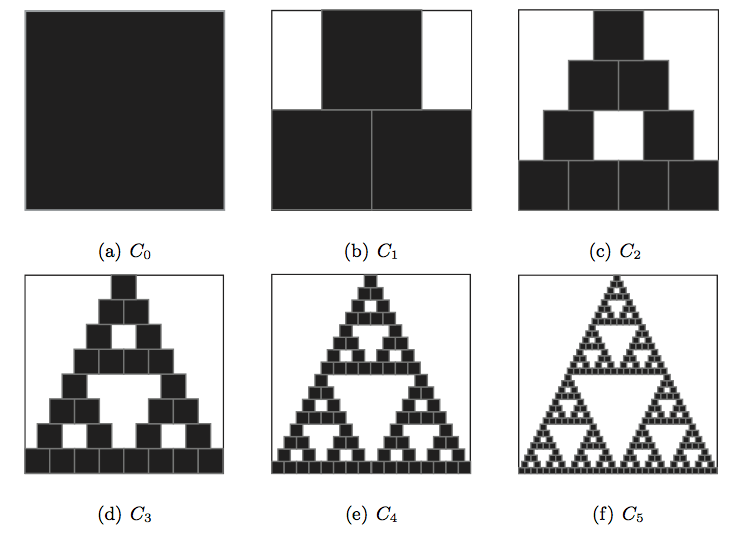
We have announced that we would experiment that the Sierpiński carpet is the only fixed point of this function. Let us try with a square ![]() as in Figure 1(a). Its image is
as in Figure 1(a). Its image is ![]() in Figure 1(b). We apply the same process to
in Figure 1(b). We apply the same process to ![]() and get
and get ![]() ,
, ![]() –
–![]() . (Figure 1 (c)-(f)).
. (Figure 1 (c)-(f)).
We observe three things:
- None of the sets
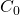 , …,
, …, 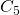 is a fixed point of
is a fixed point of 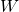 .
.
- We could have continued the process indefinitely, thus producing an infinite sequence of sets
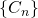 , where
, where 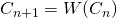 .
.
- The sequence
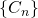 seems to converge rapidly to the Sierpiński carpet. Indeed, our eye cannot distinguish
seems to converge rapidly to the Sierpiński carpet. Indeed, our eye cannot distinguish 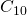 from
from  . So, instead of
. So, instead of  on our image, the program reconstructing our image can just produce
on our image, the program reconstructing our image can just produce 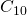 . And, if a better resolution were needed, then we would use the same program and ask it to stop at
. And, if a better resolution were needed, then we would use the same program and ask it to stop at 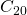 , or
, or 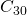 . So the same very small program can reconstruct
. So the same very small program can reconstruct  to any precision!
to any precision!
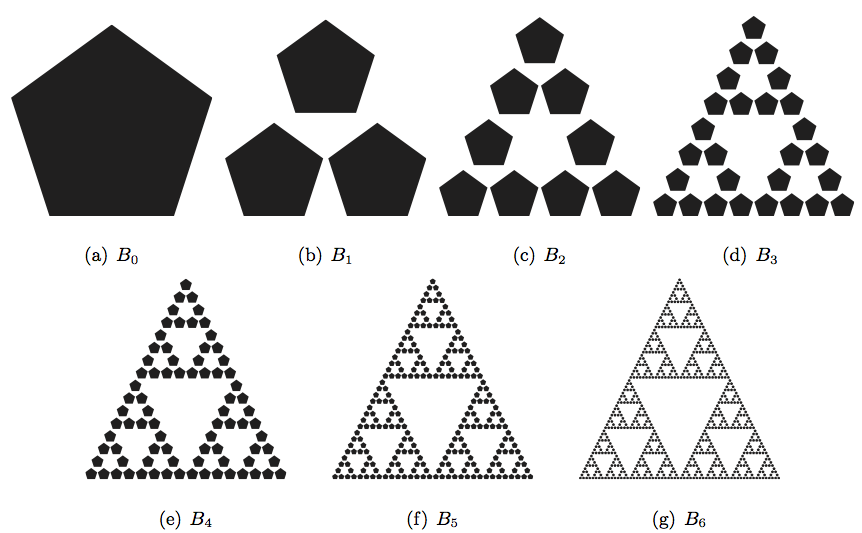
Not only that, but we can experiment that it works with any initial set! A second example iterating a pentagon appears in Figure 2. The same remarks (i), (ii) and (iii) as above apply to this example.
We have seen that the Banach fixed point theorem applies to contractions on complete metric spaces. We have defined the function ![]() in (2) on subsets of the place. For the metric space, we will take
in (2) on subsets of the place. For the metric space, we will take ![]() as the set of (closed) bounded subsets of the place. We will introduce a distance on
as the set of (closed) bounded subsets of the place. We will introduce a distance on ![]() called the Hausdorff distance. The definition of the Hausdorff distance
called the Hausdorff distance. The definition of the Hausdorff distance ![]() , between two subsets
, between two subsets ![]() and
and ![]() is a complicated and obscure formula, so we we explain the notion in another way. We start by explaining what meaning we want to give to the statement
is a complicated and obscure formula, so we we explain the notion in another way. We start by explaining what meaning we want to give to the statement
![]()
(even if we have not defined what ![]() is!) It would just mean that if our eye has a precision of
is!) It would just mean that if our eye has a precision of ![]() , then it cannot distinguish
, then it cannot distinguish ![]() from
from ![]() . In mathematical terms, then
. In mathematical terms, then ![]() should mean
should mean
(3) ![]()
(Here ![]() is the usual Euclidean distance on
is the usual Euclidean distance on ![]() .) This allows to give the indirect definition.
.) This allows to give the indirect definition.
Definition. The Hausdorff distance between two closed bounded sets ![]() and
and ![]() is the minimum of all
is the minimum of all ![]() such that (3) is satisfied.
such that (3) is satisfied.
We can now convince ourselves that the function ![]() is a contraction. Indeed, suppose that
is a contraction. Indeed, suppose that ![]() . Then we can show that
. Then we can show that ![]() . Let
. Let ![]() . Then there exist
. Then there exist ![]() and
and ![]() such that
such that ![]() . Since
. Since ![]() , there exists
, there exists ![]() such that
such that ![]() . Let
. Let ![]() . Then
. Then ![]() and
and ![]() . Similarly, if we start with
. Similarly, if we start with ![]() then there exists
then there exists ![]() such that
such that ![]() .
.
This process has been adapted to the compression of real images (see [K] or [RS]). The method produces high quality images when the image has some fractal character. However the rate of compression is not as good and not as flexible as the JPEG format. Also, the encoding process (transforming the image in a program to reconstruct it) is still too tedious to be of practical interest. However, the simplicity of its idea together with its power remains quite striking.
4. A surprising application: the PageRank algorithm
Google’s success as a search engine comes from its algorithm: the PageRank algorithm. In this algorithm, one computes a fixed point of a linear operator on ![]() which is a contraction, and this fixed point (which is a vector) yields the ordering of the pages. In practice, the fixed point (which is an eigenvector of the eigenvalue
which is a contraction, and this fixed point (which is a vector) yields the ordering of the pages. In practice, the fixed point (which is an eigenvector of the eigenvalue ![]() ) is calculated approximately as
) is calculated approximately as ![]() for
for ![]() sufficiently large. We invite the interested reader to look at the details in the vignette on How Google works?.
sufficiently large. We invite the interested reader to look at the details in the vignette on How Google works?.
5. Conclusion
What we have experienced inside that vignette is how, starting from a simple game, we can discover very powerful ideas that may lead to mathematical and technological breakthroughs. When we are looking for a unique solution of a problem, it has now become a standard method in many domains of mathematics to try to see if the solution of the problem can be characterized as the unique fixed point of an operator especially constructed for that purpose.
We have seen that the advantage of this approach is that the theorem provides an efficient practical method to construct the solution object as the limit of a sequence since the convergence is fast.
Analysis is the study of functions. Functions are usually defined on numbers. In multivariate calculus, we generalize the notion of functions to vectors which are elements of ![]() . But, why stop with elements of
. But, why stop with elements of ![]() ? We have also experienced that mathematicians like to generalize the notion of functions, and allow them to be defined, for instance, on sets of sets, and on sets of functions, etc. Doing analysis on sets of functions has now become an important chapter of modern analysis, called functional analysis, which is standard in graduate studies.
? We have also experienced that mathematicians like to generalize the notion of functions, and allow them to be defined, for instance, on sets of sets, and on sets of functions, etc. Doing analysis on sets of functions has now become an important chapter of modern analysis, called functional analysis, which is standard in graduate studies.
You are invited to make the link with some of the iterative processes you have encountered. For instance, it could have been the iterative processes in dimension 1 associated to the H\’eron sequences to obtain square roots. The rapid geometric convergence can also be understood from the point of view presented here.
Bibliography
[B] M. F. Barnsley, Fractals everywhere, San Diego, Academic Press, 1988.
[K] J. Kominek, Advances in fractal compression for
multimedia applications, Multimedia Systems Journal, vol. 5,
n![]() 4, 1997, 255–270.
4, 1997, 255–270.
[R] C. Rousseau, Point fixe de Banach (in French), Accromath 5, hiver-printemps 2010 (www.accromath.ca).
[R2] C. Rousseau, How Google works? Klein vignette (www.kleinproject.org).
[RS] C. Rousseau and Y. Saint-Aubin, Mathematics and
technology, SUMAT Series, Springer-Verlag, 2008 (A French version of the book, Mathéematiques et technologie, exists, published in the same series.)