Qual è l’impacchettamento più fitto delle sfere Keplero ha congetturato che fosse quello che si osserva nelle arance al mercato e che è chiamato reticolo cubico a facce centrate (Figura 1). Al Congresso Internazionale dei matematici nel 1900, David Hilbert ha tenuto una conferenza molto famosa nella quale ha presentato 23 problemi che avrebbero avuto una profonda significatività per il progresso dellascienza matematica nel ventesimo secolo.
Il problema dell’impacchettamento più denso delle sfere, chiamato anche congettura di Keplero, fa parte del 18° problema di Hilbert. La congettura di Keplero è stata dimostrata soltanto nel 1998 da Thomas Hales e i dettagli della dimostrazione sono stati pubblicati nel 2006.
1. Come possiamo affrontare questo tipo di problemi?
Consideriamo configurazioni diverse di sfere uguali (palle solide) nello spazio e, in ciascun caso, calcoliamo la densità dell’impacchettamento, cioè calcoliamo la frazione del volume totale che è occupato dalle sfere. Chiameremo ![]() la densità massima di un impacchettamento di sfere in dimensione
la densità massima di un impacchettamento di sfere in dimensione ![]() . Sicuramente, questa densità dipende dalla forma della regione. Per evitare questo, consideriamo regioni molto grandi, in modo da rendere trascurabile l’effetto della frontiera. Keplero ha congetturato nel 1611 che la configurazione più densa è quella che si osserva con le arance in un negozio di frutta. Quindi, perché c’è voluto così tanto tempo per dimostrare questa congettura? Il problema è che esiste un numero infinito di possibili configurazioni delle sfere. Ogni volta che consideriamo una configurazione, possiamo mostrare che la sua densità è minore o uguale di quella che si può vedere al mercato. Ma il problema è che possiamo descrivere solo un numero finito di configurazioni. E, anche con una singola configurazione, il calcolo della sua densità può essere difficile o impossibile se la configurazione non è periodica.
. Sicuramente, questa densità dipende dalla forma della regione. Per evitare questo, consideriamo regioni molto grandi, in modo da rendere trascurabile l’effetto della frontiera. Keplero ha congetturato nel 1611 che la configurazione più densa è quella che si osserva con le arance in un negozio di frutta. Quindi, perché c’è voluto così tanto tempo per dimostrare questa congettura? Il problema è che esiste un numero infinito di possibili configurazioni delle sfere. Ogni volta che consideriamo una configurazione, possiamo mostrare che la sua densità è minore o uguale di quella che si può vedere al mercato. Ma il problema è che possiamo descrivere solo un numero finito di configurazioni. E, anche con una singola configurazione, il calcolo della sua densità può essere difficile o impossibile se la configurazione non è periodica.
Il problema dell’impacchettamento più denso delle sfere esiste in ogni dimensione. È stato risolto nel 1890 per le palle solide bidimensionali. L’impacchettamento di sfere in dimensioni superiori ha applicazioni, ad esempio, nei codici di correzione degli errori.
Già in dimensione 2 incontriamo le stesse due difficoltà: possiamo enumerare tutte le configurazioni e, in più, molte di queste possono non essere periodiche. Mostreremo come affrontiamo queste difficoltà e il fatto che l’impacchettamento di Figura 1(b) è la configurazione più densa di tutte le configurazioni. Spiegheremo poi le difficoltà di generalizzare la dimostrazione al caso tridimensionale e termineremo con qualche cenno per le dimensioni superiori.
2. Il caso bidimensionale
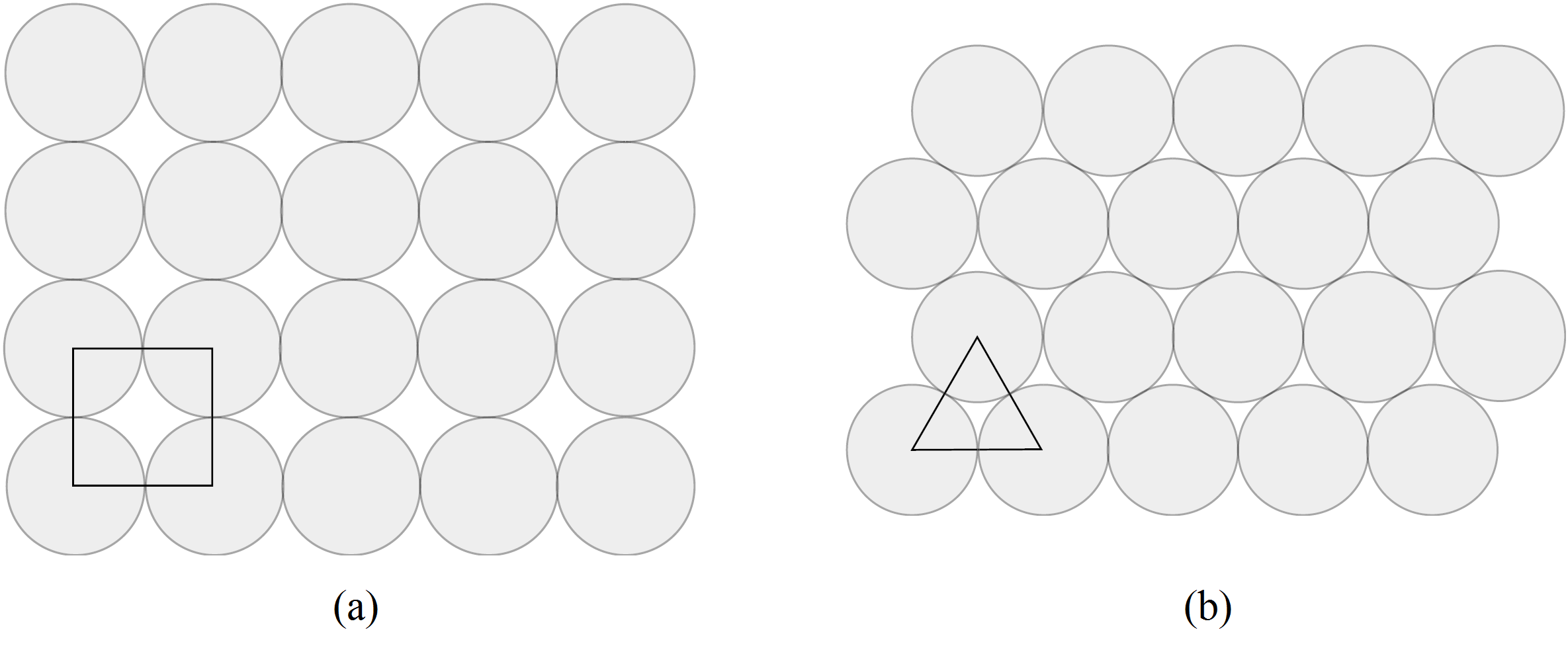
Consideriamo i due impacchettamenti di dischi in Figura 1. È un semplice esercizio calcolare la proporzione di ciascun quadrato coperto dalle porzioni di dischi nel caso (a) e quella di ciascun triangolo coperto dalle porzioni di dischi nel caso (b). Se facciamo così, notiamo che la seconda confezione è più densa. Infatti, l’impacchettamento (a) ha densità![]() e quello (b) ha densità
e quello (b) ha densità
![]()
Ogni volta che consideriamo un impacchettamento periodico, possiamo mostrare che è meno denso di quello mostrato in Figura 1 (b).
Ma, come mostriamo che questo vale per qualsiasi impacchettamento?
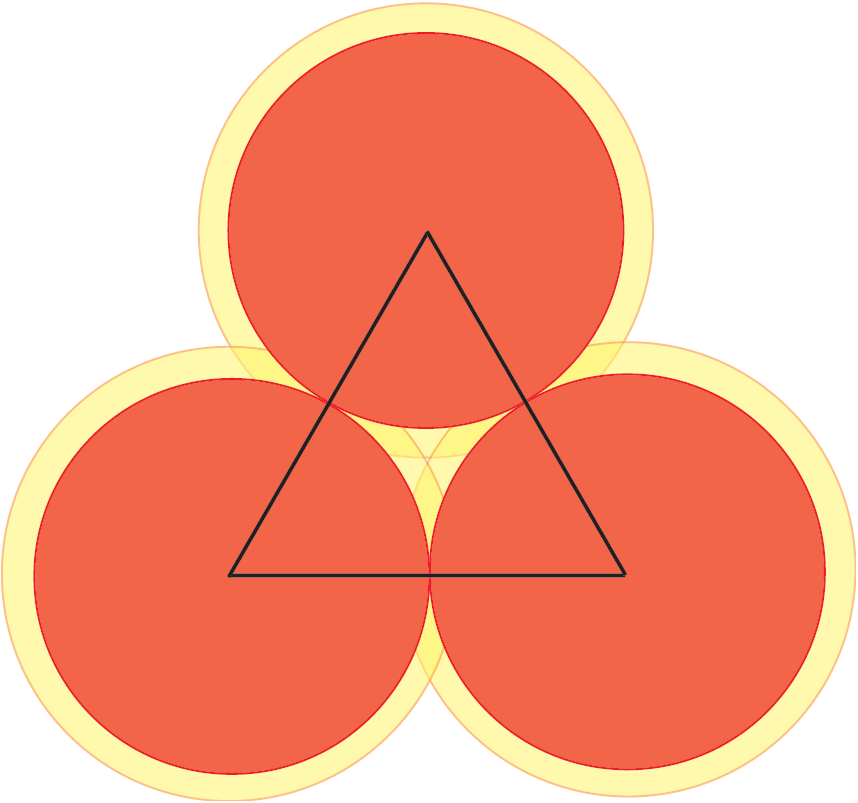
Qui entra in gioco un’idea geniale, che risale al 1890, di un matematico norvegese, Axel Thue. Dividiamo il piano in regioni locali e mostriamo che, in tutte le regioni, la densità è minore o uguale di ![]() Guardiamo la Figura 2. Abbiamo tre dischi che non possono essere più vicini tra loro di quanto già non siano. Ora, guardiamo al triangolo coi vertici nei centri dei dischi. All’interno di questo triangolo, c’è una piccola regione non coperta dai dischi. Se, comunque, allarghiamo i dischi di un fattore
Guardiamo la Figura 2. Abbiamo tre dischi che non possono essere più vicini tra loro di quanto già non siano. Ora, guardiamo al triangolo coi vertici nei centri dei dischi. All’interno di questo triangolo, c’è una piccola regione non coperta dai dischi. Se, comunque, allarghiamo i dischi di un fattore ![]() , allora i dischi allargati riempiono completamente il triangolo e questo fattore
, allora i dischi allargati riempiono completamente il triangolo e questo fattore ![]() è il minimo che raggiunge questo obiettivo.
è il minimo che raggiunge questo obiettivo.
Useremo questo trucco per dividere il piano in regioni adeguate. Consideriamo un impacchettamento del piano coi dischi di raggio ![]() . Per ciascun disco, inseriamo al suo interno un disco dello stesso centro e raggio
. Per ciascun disco, inseriamo al suo interno un disco dello stesso centro e raggio ![]() , che chiamiamo un disco largo. Ora, possiamo definire le nostre tre regioni. La prima regione è il complementare dell’unione dei dischi larghi. Ovviamente, la densità di questa regione è
, che chiamiamo un disco largo. Ora, possiamo definire le nostre tre regioni. La prima regione è il complementare dell’unione dei dischi larghi. Ovviamente, la densità di questa regione è ![]() . A seconda della distanza tra i centri dei dischi, i dischi larghi possono sovrapporsi o meno. Quando i dischi largi si sovrappongono, le loro circonferenze di bordo si intersecano. Uniamo questi punti di intersezione ai centri dei dischi. Questo processo divide i dischi larghi in settori. Ci sono due tipi di settori:
. A seconda della distanza tra i centri dei dischi, i dischi larghi possono sovrapporsi o meno. Quando i dischi largi si sovrappongono, le loro circonferenze di bordo si intersecano. Uniamo questi punti di intersezione ai centri dei dischi. Questo processo divide i dischi larghi in settori. Ci sono due tipi di settori:
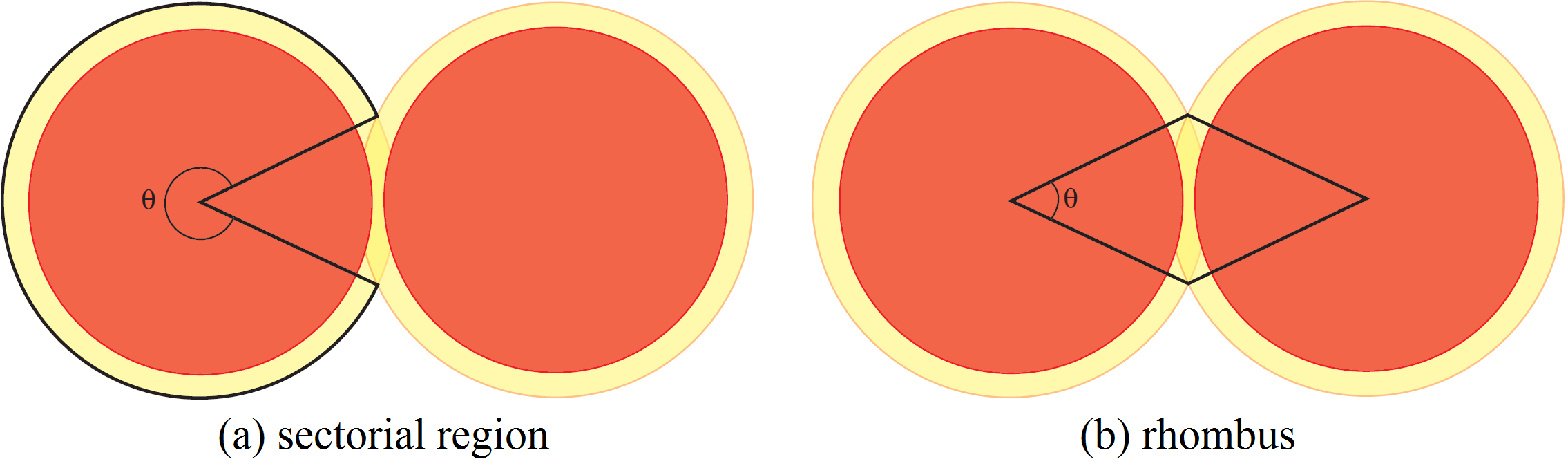
- i settori in cui il disco largo non ha sovrapposizioni con un altro disco largo (vedi Figura 3 (a)). In ciascuno di questi settori la densità è quindi uguale a
![Rendered by QuickLaTeX.com \[\frac{1}{c^2}=\frac{3}{4};\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-7a5b412bf3acabb8882fdc0cf1c6347e_l3.png)
- i settori in cui i dischi larghi si sovrappongono come mostrato in Figura 3 (b). Prendiamo questi settori a coppie come in figura. L’unione dei due settori è un rombo e abbiamo bisogno di considerare solo la densità all’interno di questo rombo. Poiché la distanza tra i centri dei dischi è al massimo
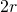 perché i dischi non si sovrappongono, un calcolo mostra che l’angolo massimo dei settori è
perché i dischi non si sovrappongono, un calcolo mostra che l’angolo massimo dei settori è 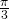 . Sia
. Sia 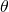 l’angolo del settore. La densità all’interno del rombo dipende da
l’angolo del settore. La densità all’interno del rombo dipende da 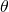 : essa è data dal quoziente delle aree dei due settori dei dischi diviso l’area del rombo. Ciascun settore di un disco ha area pari a
: essa è data dal quoziente delle aree dei due settori dei dischi diviso l’area del rombo. Ciascun settore di un disco ha area pari a 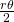 . Quindi, l’area coperta dai dischi all’interno del rombo è
. Quindi, l’area coperta dai dischi all’interno del rombo è 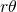 . L’area di un rombo di lato
. L’area di un rombo di lato 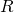 e angolo
e angolo 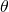 si trova decomponendo il rombo in triangoli. Essa è uguale a
si trova decomponendo il rombo in triangoli. Essa è uguale a 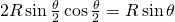 . Quindi la densità è
. Quindi la densità è
![Rendered by QuickLaTeX.com \[\mu(\theta)=\frac{r^2\theta}{R^2\sin\theta}=\frac{3\theta}{4\sin\theta}.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-90f24f10ca630f0e9d01b943b639c102_l3.png)
È sufficiente studiare la funzione
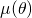 su
su ![Rendered by QuickLaTeX.com [0,\frac{\pi}3]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-97108dd255a2234a8ad4dd9ed1cb498f_l3.png) e vedere che raggiunge il suo massimo per
e vedere che raggiunge il suo massimo per 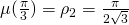 . Infatti,
. Infatti, 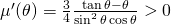 poiché
poiché 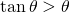 .
.Questa dimostrazione è estremamente elegante. Esaminiamone in dettaglio alcune delle sue caratteristiche. La densità migliore è
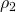 . Essa è anche la migliore densità localmente in ciascuna delle regioni del piano che abbiamo considerato.
. Essa è anche la migliore densità localmente in ciascuna delle regioni del piano che abbiamo considerato.C’è un altro modo di partizionare il piano in regioni. È il Diagramma di Voronoi dell’insieme dei centri dei dischi. Considerando un insieme
 di punti nel piano, il diagramma di Voronoi di
di punti nel piano, il diagramma di Voronoi di  è la partizione del piano in regioni, ognuna attaccata a ciascun punto
è la partizione del piano in regioni, ognuna attaccata a ciascun punto 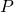 di
di  , tale che la regione attaccata a un punto dato
, tale che la regione attaccata a un punto dato 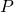 è l’insieme di punti nel piano che sono più vicini a
è l’insieme di punti nel piano che sono più vicini a 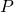 di qualsiasi altro punto
di qualsiasi altro punto 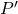 di
di  . Queste regioni sono chiamate celle di Voronoi. Poiché la mediana di un segmento
. Queste regioni sono chiamate celle di Voronoi. Poiché la mediana di un segmento 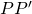 è il luogo geometrico dei punti che sono equidistanti da
è il luogo geometrico dei punti che sono equidistanti da 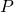 e da
e da 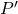 , non è sorprendente che il diagramma di Voronoi di un insieme di punti come in Figura 4, con un lato comune tra una coppia di celle di Voronoi adiacenti, sia dato da una retta della mediana dei punti di
, non è sorprendente che il diagramma di Voronoi di un insieme di punti come in Figura 4, con un lato comune tra una coppia di celle di Voronoi adiacenti, sia dato da una retta della mediana dei punti di  attaccati alle due celle.
attaccati alle due celle.Quando abbiamo un impacchettamento di dischi nel piano, è naturale guardare al diagramma di Voronoi dell’insieme dei centri dei dischi. Torniamo indietro ai due esempi di Figura 1. Sulla sinistra, le celle di Voronoi sono quadrati. Sulla destra, esse sono esagoni, e la densità di ciascun disco all’interno della sua cella esagonale di Voronoi è esattamente uguale a
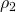 . Notiamo che, se contorniamo un dato disco con dischi che non si sovrappongono dello stesso raggio, la cella di Voronoi di area minima è l’esagono circoscritto.
. Notiamo che, se contorniamo un dato disco con dischi che non si sovrappongono dello stesso raggio, la cella di Voronoi di area minima è l’esagono circoscritto.
3. Il caso tridimensionale
3.1. La difficoltà del problema
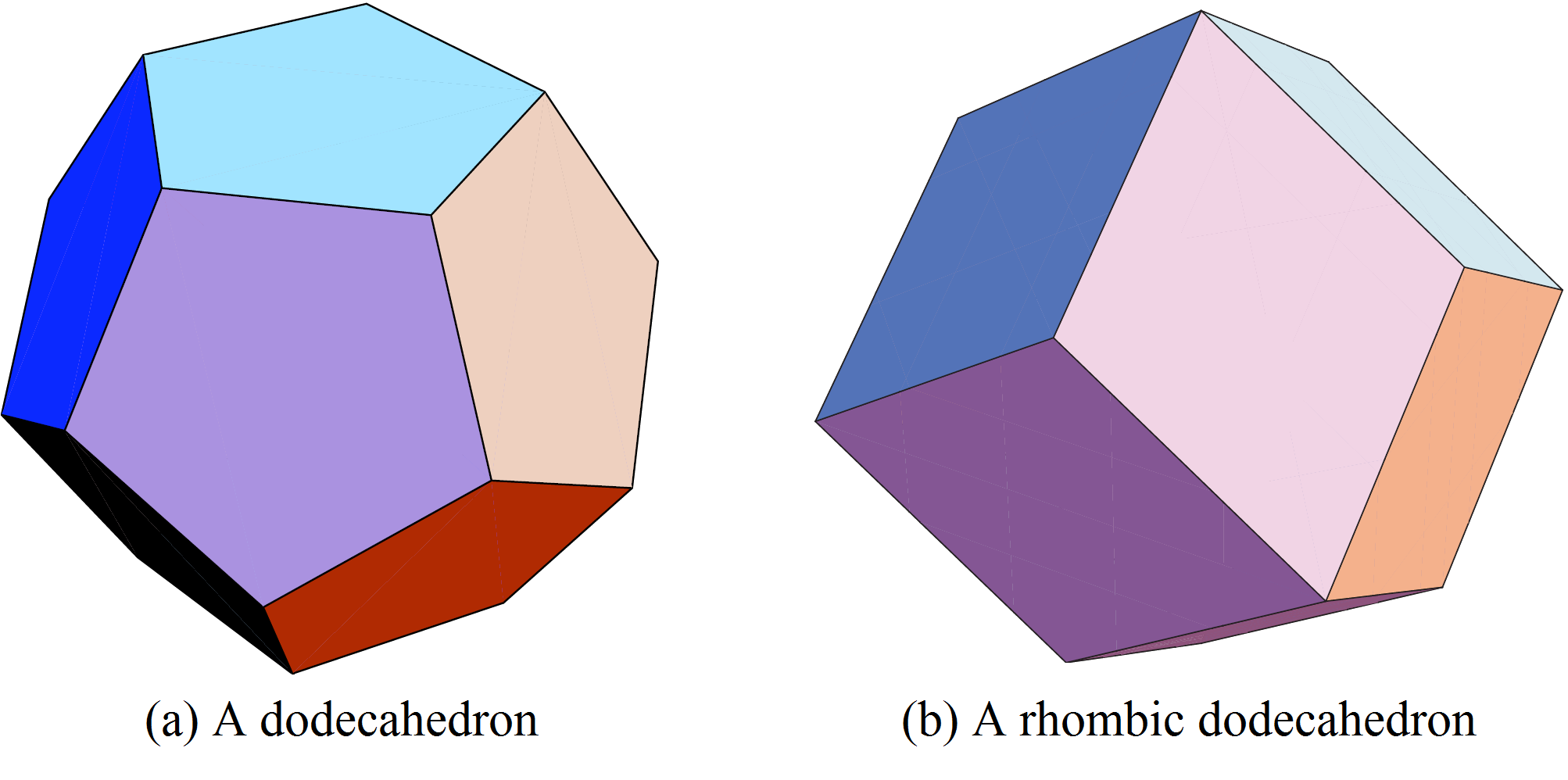
È naturale provare a generalizzare questa idea al caso tridimensionale. Il diagramma di Voronoi può essere definito come prima. Le sue celle vicine sono poliedri convessi. Circondiamo una sfera con sfere tangenti. Possiamo piazzare 12 sfere. Ma, al contrario del caso planare, c’è ancora spazio attorno alla prima sfera. Possiamo provare a muoverci attorno alle 12 sfere tangenti e vedere se possiamo piazzare una tredicesima. È stato provato da Thomas Hales che ciò non è possibile. Ma esistono molti modi non equivalenti di posizionare 12 sfere tangenti ad una data ed esse non producono celle di Voronoi dello stesso volume! La configurazione ottimale per minimizzare il volume della cella di Voronoi è che le 12 sfere siano tangenti alla sfera originale nei vertici del dodecaedro inscritto (Figura (5 (a))). Questo è stato congetturato da Fejer Toth nel 1940 e definitivamente dimostrato da uno studente universitario, Sean McLughlin nel 1999!
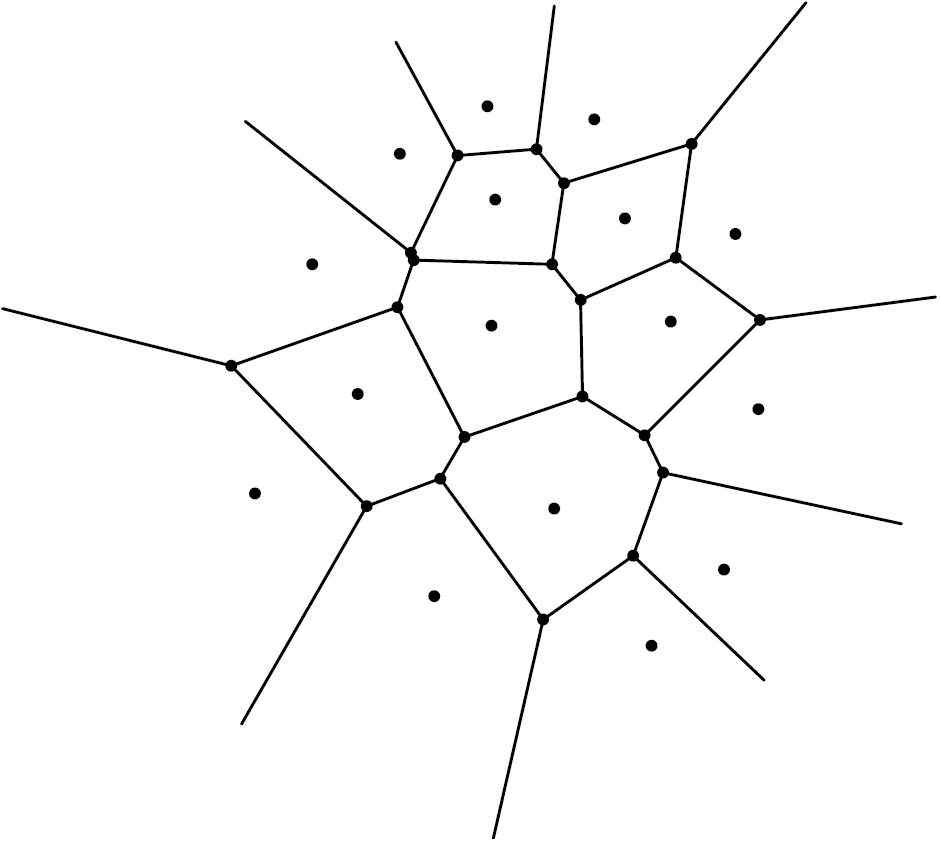
Figura 4: Un diagramma di Voronoi che attacca, a ciascuno dei punti
dell’insieme S, la sua cella di Voronoi
Quindi la cella di Voronoi di una sfera data è un dodecaedro circoscritto alla sfera. È possibile calcolare la densità della sfera all’interno della sua cella di Voronoi. È inferiore alla densità dell’ impacchettamento delle arance al mercato! Allora, possiamo fare di meglio?
No!
Poiché è impossibile riempire lo spazio con dodecaedri non sovrapposti: esiste necessariamente dello spazio vuoto tra loro. Perciò, vediamo che il caso tridimensionale è molto più complesso di quello bidimensionale, perché la soluzione ottimale locale non coincide con quella ottimale globale.
Per la soluzione ottimale di cui studieremo la geometria nella sezione successiva, i centri delle sfere sono posizionati ai vertici del reticolo cubico a facce centrate. Le celle di Voronoi corrispondenti sono dodecaedri romboidali, come mostrato in Figura 5(b).
I dodecaedri romboidali possono tassellare lo spazio in modo regolare, e tali tassellazioni sono osservate in cristallografia.
La dimostrazione del fatto che questo impacchettamento è quello ottimale è stata portata a termine da Thomas Hales con l’aiuto del suo studente Samuel Ferguson nel 1998 (la dimostrazione completa è stata pubblicata solo nel 2006). La dimostrazione, una dimostrazione assistita dal computer, è un reale tour-de-force. Anche se non siamo in grado di imitare la dimostrazione del caso bidimensionale, lo spirito rimane lo stesso: la dimostrazione consiste nel decomporre lo spazio in regioni di un numero finito di tipi e di calcolare la densità in ciascuna di queste regioni. Il programma (pesante) è disponibile sul web per coloro che volessero studiarlo o testarlo.
3.2 La geometria dell’impacchettamento ottimale
Immaginiamo una tassellazione con cubi dello spazio tridimensionale. Ora, per ciascun cubo, posizioniamo una sfera centrata in ciascun vertice e una sfera centrata al centro di ciascuna delle facce, come mostrato in Figura 6. Prendiamo il raggio delle sfere il più grande possibile così che le sfere non si intersechino. Se a è la lunghezza di uno spigolo del cubo, allora è chiaro, dalla Figura 6(b), che il raggio dei cerchi dovrebbe essere ![]() . Da questo possiamo calcolare la densità dell’impacchettamento. Infatti, per ogni sfera centrata in un vertice, un ottavo di una sfera giace all’interno del cubo. Poiché ci sono otto vertici, questo fa aumentare il volume di una sfera. Per ciascuna sfera centrata nel centro di una faccia, metà di essa giace all’interno del cubo.
. Da questo possiamo calcolare la densità dell’impacchettamento. Infatti, per ogni sfera centrata in un vertice, un ottavo di una sfera giace all’interno del cubo. Poiché ci sono otto vertici, questo fa aumentare il volume di una sfera. Per ciascuna sfera centrata nel centro di una faccia, metà di essa giace all’interno del cubo.
Poiché esistono sei facce, questo fa aumentare il volume di tre sfere. Quindi, la densità è il volume di quattro sfere diviso per il volume del cubo. Il volume di ciascuna sfera è ![]() e il volume del cubo è
e il volume del cubo è ![]() . Quindi, la densità è
. Quindi, la densità è
![]()
Come si può ottenere questo impacchettamento? Allo stesso modo di quando impiliamo le arance: mettiamo un primo strato di sfere come in Figura 1(b). Sopra a questo, mettiamo un secondo strato con un cambiamento in una direzione, per esempio nella direzione in alto a destra. Il terzo livello giace sopra al secondo con un cambiamento nella stessa direzione, etc. Questo conduce a una domanda. Potremmo modificare la direzione del cambiamento tra i differenti livelli senza cambiare la densità? Si, possiamo, ma il reticolo corrispondente dei centri non sarà uno cubico a facce centrate. Questo vuol dire che l’impacchettamento che dà la densità più elevata non è unico.
Non è ovvio che l’impacchettamento usuale delle arance corrisponda ad un reticolo cubico a facce centrate. Infatti, guardando alla Figura 6(b), vediamo che dovremmo avere delle rette perpendicolari di centri allineati di sfere. È un buon esercizio di visualizzazione per capire che queste linee, infatti, esistono nell’impacchettamento usuale delle arance, ma che nessuno di esse giace nei piani orizzontali. Infatti, il piano di Figura 1(b) è un piano inclinato che attraversa i centri delle tre facce adiacenti a un vertice del cubo di Figura 6(a). In Figura 7, rappresentiamo l’impacchettamento di quattro livelli, come mostrato in Figura 1(b), uno sopra all’altro. Le due rette che attraversano i centri delle sfere sono ortogonali.
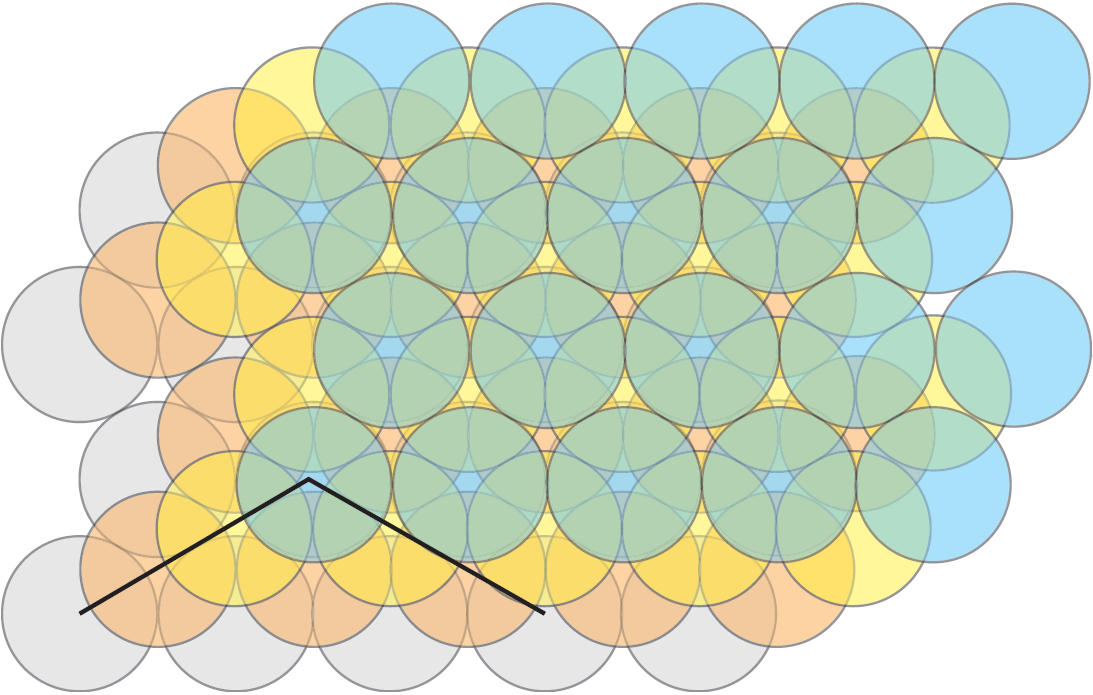
Figura 7: Quattro livelli di sfere del tipo di Figura 1(b), uno sopra all’altro
e due rette perpendicolari passanti per i centri
4. Sviluppi ulteriori
4.1 Applicazioni in cristallografia
La domanda dell’impacchettamento più denso delle sfere fu posta a Johannes Keplero da Thomas Harriot alla fine del 16-esimo secolo. Già a quel tempo, Harriot credeva nell’esistenza di atomi ed era interessato a come essi fossero disposti fra loro. Quando l’organizzazione degli atomi in un materiale è regolare, i chimici dicono che questo materiale è un cristallo. I materiali pesanti, come i metalli, spesso hanno atomi organizzati nei punti del reticolo cubico a facce centrate. Esistono anche altre disposizioni regolari meno dense. Uno degli impacchettamenti regolari meno densi è quello cubico semplice, in cui gli atomi sono posizionati ai vertici dei cubi. C’è solo un elemento chimico con questa configurazione di atomi, detto polonio radioattivo (Maggiori dettagli in [4]).
4.2 Impacchettamenti casuali
Se sistemi le arance attentamente in larghe scatole usando il modello del reticolo cubico a facce centrate sopra descritto, allora otterrai una densità pari a ![]() Ma, se sei in ritardo e devi solo metterle velocemente nella scatola, qual è la densità che ottieni? Questo è quello che si chiama impacchettamento casuale. Di certo, la densità non è sempre la stessa. Infatti, se agiti la tua scatola, probabilmente aumenterai la densità. Ma fino a che punto? Gli esperimenti mostrano che la densità varia dal 55% (impacchettamento casuale libero) a un massimo pari al 63; 4% (impacchettamento casuale chiuso). La scoperta del massimo limite era argomento di una lettera di Song, Wang e Maske [3], nella rivista Natura (2008).
Ma, se sei in ritardo e devi solo metterle velocemente nella scatola, qual è la densità che ottieni? Questo è quello che si chiama impacchettamento casuale. Di certo, la densità non è sempre la stessa. Infatti, se agiti la tua scatola, probabilmente aumenterai la densità. Ma fino a che punto? Gli esperimenti mostrano che la densità varia dal 55% (impacchettamento casuale libero) a un massimo pari al 63; 4% (impacchettamento casuale chiuso). La scoperta del massimo limite era argomento di una lettera di Song, Wang e Maske [3], nella rivista Natura (2008).
4.3 Impacchettamenti di altri oggetti diversi dalle sfere
È possibile ottenere una densità più elevata di 3 se sostituiamo le sfere, ad esempio, con degli ellissoidi. L’articolo [1] mostra che la densità dell’impacchettamento casuale chiuso degli sferoidi, simili all’aspetto degli M&M’s, può variare tra 0; 68 e 0; 71 e che la densità per gli ellissoidi, simili agli M&M’s per altri aspetti, può arrivare a 0; 74. Le densità dell’impacchettamento casuale sono importanti per l’industria quando l’impacchettamento di oggetti identici (per esempio quello di caramelle o di pastiglie) è automatizzato. In particolare, la densità può variare durante il trasporto.
4.4 Un accenno sulle dimensioni superiori
In dimensione superiore, gli impacchettamenti regolari e più densi di ipersfere sono noti fino alla dimensione 8, e, invece, si conosce molto poco riguardo a quelli non regolari.
Un’applicazione dell’impacchettamento di sfere in dimensioni superiori è finalizzata a produrre codici correttori di errori. Il principio di un codice correttore di errori è codificare le lettere o le parole in sequenze di simboli, chiamate parole in codice, che differiscono l’uno dall’altro per al massimo ![]() simboli. Quindi, se si presentano meno di
simboli. Quindi, se si presentano meno di ![]() errori nella trasmissione di una parola in codice, allora esiste al massimo una parola in codice a distanza minore di
errori nella trasmissione di una parola in codice, allora esiste al massimo una parola in codice a distanza minore di ![]() dalla parola ricevuta ed è possibile una correzione. Nei codici correttori di errori, usando impacchettamenti di sfere, trasformiamo le lettere del codice in tuple di coordinate di centri di sfere che non si sovrappongono. Se le sfere hanno raggio
dalla parola ricevuta ed è possibile una correzione. Nei codici correttori di errori, usando impacchettamenti di sfere, trasformiamo le lettere del codice in tuple di coordinate di centri di sfere che non si sovrappongono. Se le sfere hanno raggio ![]() , allora è possibile correggere meno di
, allora è possibile correggere meno di ![]() errori.
errori.
4.5 La domanda successiva…
Ora tocca a voi fare domande a noi. Come avete visto, ci sono molte semplici questioni con importanti applicazioni e le cui risposte sofisticate sono pubblicate in alcune delle riviste scientifiche più importanti, come Natura, Scienze e gli Annali della Matematica.
5. La validità delle dimostrazioni assistite dal computer
La dimostrazione che l’impacchettamento più denso dei dischi nel caso bidimensionale è ![]() 2 mostra che è possibile dare dimostrazioni rigorose di risultati in cui c’è un numero infinito di casi da analizzare. È una dimostrazione che ciascuno di voi può fare. Ma chi può dimostrare che
2 mostra che è possibile dare dimostrazioni rigorose di risultati in cui c’è un numero infinito di casi da analizzare. È una dimostrazione che ciascuno di voi può fare. Ma chi può dimostrare che ![]() ? È una dimostrazione complessa con
? È una dimostrazione complessa con ![]() casi da analizzare e ciascun caso è così difficile che deve essere fatto da un computer, per un totale di 3 Gigabyte di codice di computer. Di certo il codice è pubblico. Ma, servono molti anni agli autori per produrlo. Così chi ha sia il tempo sia le capacità per andare dentro a tutti i dettagli? Sicuramente ci sono strategie per minimizzare gli errori e Hales e Solomon ne hanno usate diverse. Per esempio, i due autori hanno scritto il programma in parallelo indipendentemente. Il programma potrebbe girare su diversi computer con differenti processori e compilatori.Le sottoroutine potrebbero usare vecchi pacchetti del software che sono stati testati per anni, etc.
casi da analizzare e ciascun caso è così difficile che deve essere fatto da un computer, per un totale di 3 Gigabyte di codice di computer. Di certo il codice è pubblico. Ma, servono molti anni agli autori per produrlo. Così chi ha sia il tempo sia le capacità per andare dentro a tutti i dettagli? Sicuramente ci sono strategie per minimizzare gli errori e Hales e Solomon ne hanno usate diverse. Per esempio, i due autori hanno scritto il programma in parallelo indipendentemente. Il programma potrebbe girare su diversi computer con differenti processori e compilatori.Le sottoroutine potrebbero usare vecchi pacchetti del software che sono stati testati per anni, etc.
Tuttavia, queste dimostrazioni rimangono controverse e c’è un lungo processo di decisione da parte della comunità scientifica per accettarle. Nel caso della dimostrazione della congettura di Keplero, la dimostrazione (abbreviata), infine, apparve nel 2005 negli Annali di Matematica, una delle più rilevanti riviste matematiche. Ma la comunità dei matematici è ancora alla ricerca di una dimostrazione più “matematica”. In parallelo, i matematici e i ricercatori nella scienza teorica del computer cercano dimostrazioni formali, cioè dimostrazioni in cui ciascun passo logico può essere provato dal computer. Per esempio, l’obiettivo del progetto Flyspeck è di produrre una dimostrazione formale della congettura di Keplero:
http://code.google.com/p/flyspeck/wiki/FlyspeckFactSheet
Il primo famoso teorema la cui dimostrazione era assistita dal computer è quello dei quattro colori che afferma che sono sufficienti quattro colori per colorare ogni mappa in modo tale che due regioni adiacenti non abbiano lo stesso colore. È stato dimostrato nel 1976 da Kenneth e Wolfgang Haken. A quel tempo, gli Annali di Matematica non avrebbero accettato di pubblicare una dimostrazione assistita dal computer. I tempi sono cambiati e il computer ha rivoluzionato la pratica della matematica.
Riferimenti bibliografici
[1] A. Donev, I. Cisse, D. Sachs, E. Variano, F.H. Stillinger, R. Connelly, S. Tarquato e P.M. Chikin, Improving the density of jammed disordered packings using ellipsoids, Science, 303 (2004), 990-993.
[2] T. Hales, Cannonballs and honeycombs, Notices of the American Mathematical Society,47 (2000), 440-449
[3] C.Song, P.Wang e H.A.Maske, A phase diagram for jammed matter, Nature, 453 (2008), 629-632.
[4] G.C. Szpiro, Kepler’s conjecture, John Wiley & Sons, Inc., 2003.


Piano e spazio vanno considerati separatamente e consentono rendimenti diversi.
Sul piano abbiamo due possibilità legate entrambe al seno : la quadrata al seno di 90°;
la triangolare al seno di 60°:
Nello spazio l’ impilaggio è possibile sempre in due modi a quadrato sfalsato o a triangolo:
la prima dipende dal seno di 45° , la seconda dal seno di 54°.
Nello spazio ,al contrario che nel piano dobbiamo tenere conto dei problemi di stabilità.
Il riferimento alla cristallografia non è pertinente per la semplice ragione che c’è molta
differenza tra una palla di cannone o arancio che sia dalla dimensione puntiforme degli atomi. Provare per credere