 Originating author is Michèle Artigue.
Originating author is Michèle Artigue.
Infinitesimals played an essential role in the emergence and development of differential and integral calculus. The evident productivity of this calculus did not prevent recurrent and fierce debates about the nature of these objects and the legitimacy of their use. At the end of the 19th century, when the construction of real numbers from integers and the modern definition of the concept of limit provided a solid foundation for differential and integral calculus, infinitesimals and the associated metaphysics was rejected and their use perceived synonymous with bygone and poorly rigorous practices. However, the language of infinitesimals continued to be used, for example in physics and even in mathematics. It never completely disappeared from the informal discourse and heuristic thinking of a number of researchers.
Is this language thus really incompatible with mathematical rigour? What does it offer that is interesting and specific, which explains its permanence? Non-Standard Analysis developed in the 20th century and provided answers to these questions and enabled infinitesimals to take their revenge.
From infinitesimal calculus to non-standard analysis
In the preface of the first treaty on infinitesimal analysis published in 1696, its author, the Marquis de l’Hôpital boasts the power and ease of the new calculus that infinitesimals make possible![]() :
:

Figure 1: Cover and excerpt of the preface of the treaty by the Marquis de l’Hôpital
However, rather quickly debates arise about infinitesimals and their use. In a famous essay published in 1734, The Analyst, George Berkeley develops a fierce criticism of the use of infinitesimals, or evanescent increments, in differential calculus and Jean Le Rond d’Alembert in the l’Encyclopédie Méthodique published in 1751, tries to get free of them by relying on the intuitive idea of a limit. At the turn of the 20th century, with the development of modern analysis, this seems to be achieved. However, half a century later, the logician Abraham Robinson will rehabilitate infinitesimals and associated practices.
Abraham Robinson indeed shows that the language of infinitesimals is fully compatible with mathematical rigour. The logician Thoralf Skolem had already shown in 1934 that the set obtained by adding successive units to 0 could not be the only model of the Peano’s axioms for arithmetic, that there thus existed other models, called for that reason non-standard. In 1961, Abraham Robinson showed, by a construction based on ultra-products, the existence of a non-standard model of the field of real numbers containing numbers “infinitely large” and “infinitely small”. This was the birth of non-standard analysis (NSA). Then in 1977 Edward Nelson found how to axiomatise NSA. To do this, he added a one-place predicate symbol ![]() expressing that an object
expressing that an object ![]() is standard to the language of set theory, and three axioms to the ZFC
is standard to the language of set theory, and three axioms to the ZFC![]() axioms of set theory: the axioms of idealisation, standardisation and transfer
axioms of set theory: the axioms of idealisation, standardisation and transfer![]() , which made NSA easier to manipulate. It is on this axiomatisation called IST (Internal Set Theory) that we rely in this vignette.
, which made NSA easier to manipulate. It is on this axiomatisation called IST (Internal Set Theory) that we rely in this vignette.
These three axioms have important consequences. It results, for example, from the axiom of transfer that two standard sets E1 and E2 are equal if and only if they have the same standard elements![]() . It also results from the same axiom that if there exists an
. It also results from the same axiom that if there exists an ![]() satisfying a classical property
satisfying a classical property ![]() (that is to say a property that can be expressed without using the predicate st), then necessarily there also exists a standard
(that is to say a property that can be expressed without using the predicate st), then necessarily there also exists a standard ![]() satisfying it. So, the objects that can be defined by a classical formula, in a unique way, are standard. Numbers and ordinary objects that we frequent in mathematics: the numbers
satisfying it. So, the objects that can be defined by a classical formula, in a unique way, are standard. Numbers and ordinary objects that we frequent in mathematics: the numbers ![]() ,
, ![]() , trigonometric and exponential functions belong to this category and are thus all standard objects, like the empty set, the set
, trigonometric and exponential functions belong to this category and are thus all standard objects, like the empty set, the set ![]() of whole numbers and the set
of whole numbers and the set ![]() of real numbers.
of real numbers.
However, to be a standard set does not imply to have only standard elements. In fact, it results from the axiom of idealisation that there exists in ![]() an integer bigger than all standard integers, thus necessarily non-standard. More generally, using the same axiom, it is easily proved that any infinite set has non-standard elements
an integer bigger than all standard integers, thus necessarily non-standard. More generally, using the same axiom, it is easily proved that any infinite set has non-standard elements![]() .
. ![]() et
et ![]() are thus standard sets containing both standard and non-standard elements. How can we represent them?
are thus standard sets containing both standard and non-standard elements. How can we represent them?
In ![]() , all standard integers come first, preceding non-standard integers. In
, all standard integers come first, preceding non-standard integers. In ![]() , the situation is more complicated. One can distinguish three categories of real numbers, according to their magnitude:
, the situation is more complicated. One can distinguish three categories of real numbers, according to their magnitude:
- The real numbers which are very small or infinitesimals (positive or negative), those whose absolute value is less than any standard positive real number,
- The real numbers which are very big or infinitely big (positive or negative), those whose absolute value is more than any standard positive real number,
- And, between them, the real numbers having a human size so to speak, often called appreciable numbers.
If a real number is infinitesimal or appreciable, it is said limited. If a real number is infinitely big, its inverse is an infinitesimal, and both of them are non-standard. Appreciable real numbers may be standard or non-standard. Let us consider for instance the real number ![]() ; adding to it an infinitesimal
; adding to it an infinitesimal ![]() different from
different from ![]() , one obtains the number
, one obtains the number ![]() also appreciable, but non-standard and infinitely close to
also appreciable, but non-standard and infinitely close to ![]() . Around each standard real number, there exists thus a cloud of infinitely close non-standard real numbers. To give account of this situation, a new relationship is introduced.
. Around each standard real number, there exists thus a cloud of infinitely close non-standard real numbers. To give account of this situation, a new relationship is introduced. ![]() is said infinitely close to y if
is said infinitely close to y if ![]() is an infinitesimal, which is noted
is an infinitesimal, which is noted ![]() . The collection of real numbers infinitely close to a given real number is called its halo. Infinitesimals are the halo of
. The collection of real numbers infinitely close to a given real number is called its halo. Infinitesimals are the halo of ![]() and each appreciable real belongs to the halo of a unique standard real number called its standard part. The real non-standard line can be represented as in Figure 2, with a blurry frontier between real numbers that are appreciable and those that are infinitely big, as the collection of appreciable real numbers does not have a maximum and the collection of infinitely big numbers does not have a minimum.
and each appreciable real belongs to the halo of a unique standard real number called its standard part. The real non-standard line can be represented as in Figure 2, with a blurry frontier between real numbers that are appreciable and those that are infinitely big, as the collection of appreciable real numbers does not have a maximum and the collection of infinitely big numbers does not have a minimum.

Figure 2 : Representation of the non-standard real line
Rules of calculation taking into account the different orders of magnitude of numbers extend those of arithmetic. Noting ![]() the infinitesimals,
the infinitesimals, ![]() the appreciable and
the appreciable and ![]() the infinitely big, one has for instance::
the infinitely big, one has for instance:: ![]() ,
, ![]() ,
, ![]() et
et ![]() , and we invite the reader of this vignette to complement the following tables where possible.
, and we invite the reader of this vignette to complement the following tables where possible.
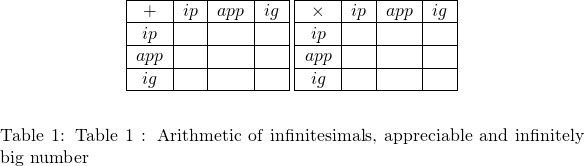
The set of real numbers still verifies the Archimede’s axiom: if ![]() and
and ![]() are positive real numbers such as
are positive real numbers such as ![]() , there exists an integer
, there exists an integer ![]() such as
such as ![]() , but of course if
, but of course if ![]() is an infinitesimal and
is an infinitesimal and ![]() is not,
is not, ![]() will be infinitely big.
will be infinitely big.
NSA and basic notions of Analysis
Within the framework of NSA, basic notions of mathematical analysis: limits, continuity, differentiability and integrability have very simple formalisations for standard objects, as shown in the table below![]() :
:

These simple formalisations without alternation of quantifiers and the ideas underlying these, allows simplified proofs of many classical theorems. We propose below a non-standard proof of the Intermediate Value Theorem as an illustration.
|
Theorem of intermediate values
Proofe : without limiting the generality of the proof, we can suppose that |
ANS also allows the justification of the technique of cutting into infinitesimal slices still used beyond the mathematics community for calculating areas, volumes, inertia moments, gravity centres…, or for modelling situations through differential equations. The example below is a very simple illustration.
Computation of the volume of the sphere:
Let ![]() be a sphere of radius
be a sphere of radius ![]() . One cuts the sphere into slices of infinitesimal thickness
. One cuts the sphere into slices of infinitesimal thickness ![]() . The volume
. The volume ![]() of the slice situated at the altitude
of the slice situated at the altitude ![]() is approximately that of the cylinder of
is approximately that of the cylinder of ![]() and hight
and hight ![]() .
.
![]()
From here, by summation it comes
![]()
![]()
and finally ![]() .
.
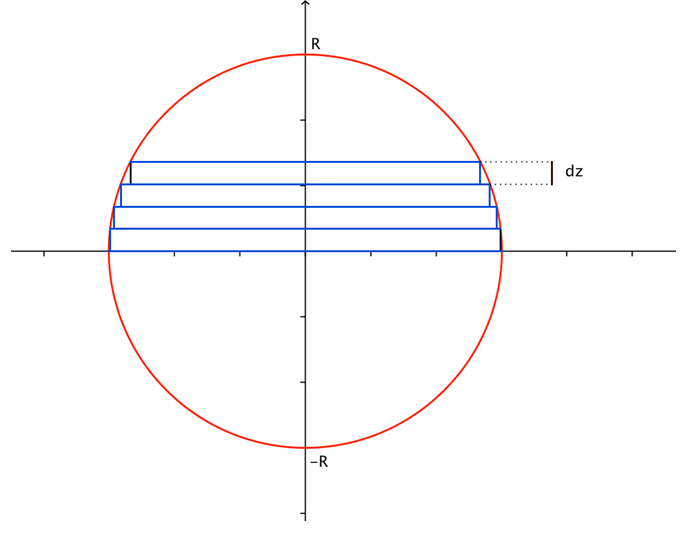
Figure 4 : The volume of the sphere
The sum of the volumes of the infinitesimal cylinders is in fact the Cauchy sum attached to the infinitesimal subdivision of step ![]() of the interval
of the interval ![]() for the area function
for the area function ![]() . Considering the non-standard definition of the integral for continuous functions, the standard part of this sum is thus equal to the integral
. Considering the non-standard definition of the integral for continuous functions, the standard part of this sum is thus equal to the integral ![]() .
.
However, the fact that this integral rightly gives the volume of the sphere results from the fact that the approximation proposed for ![]() is an equivalent of the volume of the slice, not just a number infinitely close. It would not be the case if the same approximation by cylindrical slices were used for calculating the area of the sphere for instance.
is an equivalent of the volume of the slice, not just a number infinitely close. It would not be the case if the same approximation by cylindrical slices were used for calculating the area of the sphere for instance.
The necessity of maintaining some vigilance
However, the manipulation of non-standard objects requires some vigilance. For instance, extending the definition of continuity given above to any real number and function, standard or not, one obtains a new notion, the ![]() -continuity at a point which does not necessarily correspond to our vision of continuous functions. For instance, the staircase function which takes the value
-continuity at a point which does not necessarily correspond to our vision of continuous functions. For instance, the staircase function which takes the value ![]() over negative real numbers and the value
over negative real numbers and the value ![]() over positive real numbers including
over positive real numbers including ![]() , with
, with ![]() infinitesimal different from
infinitesimal different from ![]() , is
, is ![]() -continuous in
-continuous in ![]() , as the image of any positive infinitesimal is the infinitesimal
, as the image of any positive infinitesimal is the infinitesimal ![]() . Conversely, the square function is not
. Conversely, the square function is not ![]() -continuous in
-continuous in ![]() , if
, if ![]() is infinitely big as
is infinitely big as ![]() is not infinitely close to
is not infinitely close to ![]() . In fact, for a standard function,
. In fact, for a standard function, ![]() -continuity at any point of
-continuity at any point of ![]() is equivalent to uniform continuity over
is equivalent to uniform continuity over ![]() . The calculation we have just made for the square function is a very simple proof of the fact that the square function, while being continuous over
. The calculation we have just made for the square function is a very simple proof of the fact that the square function, while being continuous over ![]() , is not uniformly continuous over
, is not uniformly continuous over ![]() .
.
The use of NSA requires also some vigilance when using the induction principle. In its usual form, it applies to classical properties; this is a consequence of the axiom of transfer, but not beyond. Consider the following reasoning, often presented as a paradox:
|
Let us
|
The principle of induction is applied here to a non-classical statement written with the predicate ![]() . This reasoning is not at all a paradox, it is simply non valid. In fact, it can be proved that in NSA, for a non classical property
. This reasoning is not at all a paradox, it is simply non valid. In fact, it can be proved that in NSA, for a non classical property ![]() , only the following reduced principle of induction is valid: if
, only the following reduced principle of induction is valid: if ![]() is true and, for any integer
is true and, for any integer ![]() ,
, ![]() implies
implies ![]() , then
, then ![]() is true for all standard integers.
is true for all standard integers.
The potential of NSA: a question still debated
As shown above, NSA rehabilitates infinitesimal numbers, the modes of computation and the intuitions they convey, but at the price of some work and vigilance. Thus what is really gained through NSA? The question is still discussed in the mathematics community as shown for instance by the Terence Tao blog that we accessed when preparing this vignette. NSA has been fruitfully used in a diversity of mathematical domains: topology, probabilities, dynamical systems… It has supported interesting modelling in automatics, ecology, and economics, for instance. In France, at the initiative of the mathematician Georges Reeb, a non-standard community developed from the late seventies, which obtained original results in various areas (cf. (Lutz et Goze, 1982), (Diener & Diener, 1995). Among the best known is the discovery of specific trajectories called «duck trajectories» in slow-fast vector fields in two and then three dimensions. We present this example below without entering into the technical details of its non-standard treatment, using the same differential equation as in (Benoît et al.,1981). The reader who is not familiar with differential equations can skip this part.
The ‘duck’ trajectories
We consider the differential equation ![]() , with
, with ![]() and
and ![]() . A classical study of this equation shows that if
. A classical study of this equation shows that if ![]() , the equation has a unique periodic solution which is a attractive limit cycle. This periodic solution disappears for
, the equation has a unique periodic solution which is a attractive limit cycle. This periodic solution disappears for ![]() and for
and for ![]() there exists an attractive stationary state
there exists an attractive stationary state ![]() . The phenomenon of the duck trajectories precedes this bifurcation in the dynamics of the equation, known as a Hopf’s bifurcation. It has been observed for very small values of
. The phenomenon of the duck trajectories precedes this bifurcation in the dynamics of the equation, known as a Hopf’s bifurcation. It has been observed for very small values of ![]() and values of a very close to
and values of a very close to ![]() . A non-standard modelling allowed the identification of the phenomenon and the characterisation of the conditions for its apparition.
. A non-standard modelling allowed the identification of the phenomenon and the characterisation of the conditions for its apparition.
First, we transform the second order differential equation into a first order system. This is done in two different ways, first by posing ![]() with
with ![]() , a particular transformation used for studying this type of equation known as Lienard’s type, second by posing
, a particular transformation used for studying this type of equation known as Lienard’s type, second by posing ![]() , the classical way of transforming an equation into a system. Thus the two systems, in which
, the classical way of transforming an equation into a system. Thus the two systems, in which ![]() is an infinitely big number:
is an infinitely big number:
![]()
![]()
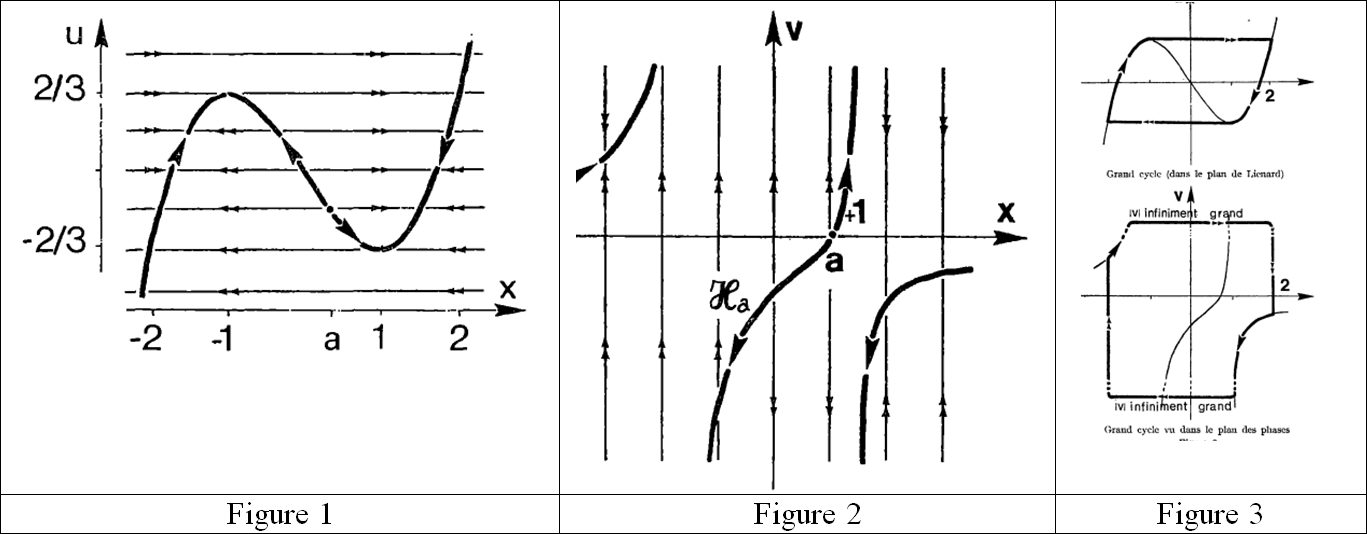
The associated vector fields in the respective planes ![]() and
and ![]() are reproduced in the figures 1 et 2 copied from (Benoît et al., 1981). They are slow-fast vector fields. For instance, the field in the plane
are reproduced in the figures 1 et 2 copied from (Benoît et al., 1981). They are slow-fast vector fields. For instance, the field in the plane ![]() or plane of Lienard is nearly horizontal outside the halo of the cubic
or plane of Lienard is nearly horizontal outside the halo of the cubic ![]() with equation
with equation ![]() whose increasing parts are attractive, due to the direction of the horizontal arrows, while the decreasing part is repulsive. The double arrows are used for remembering that these parts, nearly horizontal, are travelled with an infinitely big speed. Combining techniques of standard and non-standard analysis, especially changes in scale through using macroscopes of infinitely big ratio along one direction in the planes
whose increasing parts are attractive, due to the direction of the horizontal arrows, while the decreasing part is repulsive. The double arrows are used for remembering that these parts, nearly horizontal, are travelled with an infinitely big speed. Combining techniques of standard and non-standard analysis, especially changes in scale through using macroscopes of infinitely big ratio along one direction in the planes ![]() and
and ![]() , one can show that, when
, one can show that, when ![]() but not in the halo of
but not in the halo of ![]() , there exists a unique big cycle which is attractive (figure 3). In the plane
, there exists a unique big cycle which is attractive (figure 3). In the plane ![]() , a particle moving along this cycle, for instance starting from a point
, a particle moving along this cycle, for instance starting from a point ![]() not situated in the halo of
not situated in the halo of ![]() , reaches nearly horizontally this halo, travelling with an infinite speed, then goes down along
, reaches nearly horizontally this halo, travelling with an infinite speed, then goes down along ![]() , staying in its halo, with an appreciable speed
, staying in its halo, with an appreciable speed ![]() until it arrives in the halo of its local minimum
until it arrives in the halo of its local minimum ![]() . Then, it again takes a nearly horizontal trajectory until it reaches once again the halo of
. Then, it again takes a nearly horizontal trajectory until it reaches once again the halo of ![]() and follows this curve up to the halo of the local maximum
and follows this curve up to the halo of the local maximum ![]() ; it then starts again a nearly horizontal movement…
; it then starts again a nearly horizontal movement…
When ![]() , the situation is more complex because separate branches of the curve
, the situation is more complex because separate branches of the curve ![]() associated with
associated with ![]() in the plane
in the plane ![]() , become infinitely close. It results from that in the plane
, become infinitely close. It results from that in the plane ![]() that a solution which has followed
that a solution which has followed ![]() until the halo of
until the halo of ![]() may, for some values of a, follow a part of the repulsive part of
may, for some values of a, follow a part of the repulsive part of ![]() before becoming nearly horizontal and reaching the halo of the attractive part of
before becoming nearly horizontal and reaching the halo of the attractive part of ![]() (figure 4).
(figure 4).
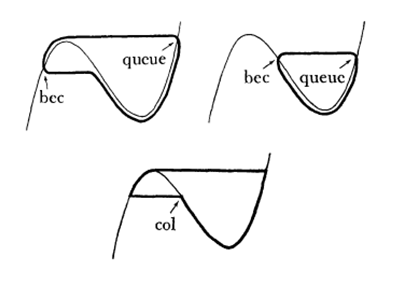
Figure 4 : Morphology of duck trajectories
Due to their form, researchers named the associated cycles duck trajectories. For instance, they showed that for any real number ![]() between
between ![]() and
and ![]() , there exists a value of a for which there exists a duck cycle whose beak abscissa is
, there exists a value of a for which there exists a duck cycle whose beak abscissa is ![]() . Without the support of a NSA modelling, the existence of such trajectories might have remained ignored. To observe them indeed it is not enough to have
. Without the support of a NSA modelling, the existence of such trajectories might have remained ignored. To observe them indeed it is not enough to have ![]() small and
small and ![]() close to
close to ![]() ; it has been proved that it is necessary to have
; it has been proved that it is necessary to have ![]() very close to
very close to ![]() , more precisely that the ratio
, more precisely that the ratio ![]() be an infinitesimal. Beyond its pure mathematical interest, the existence of duck trajectories for systems of differential equations in two and three dimensions, has had applications in extra-mathematical fields.
be an infinitesimal. Beyond its pure mathematical interest, the existence of duck trajectories for systems of differential equations in two and three dimensions, has had applications in extra-mathematical fields.
It must be stressed, however, that the original results obtained by NSA researchers have been subsequently often proved by standard methods. This is not per se surprising as IST is a conservative extension of ZFC: any theorem of the theory IST which has a classical expression is also a theorem of ZFC. Combined with the fact that many mathematicians feel that the use of these infinitesimals is a regression from which mathematics had so much difficulty to get free, this situation often leads us to consider that the NSA construction is of little utility. Those who practice NSA reject these objections. They stress the change of vision conveyed by NSA, the intuitions and modelling it makes possible, more adapted to the reality of the world than those attached to standard views. To a vision of the real number set as a homogeneous entity, they oppose the non-standard vision which puts the distinction between order of magnitudes at the core of the numerical system, reflecting the diversity of scales that sciences currently consider, and the fuzzy frontiers between them. They insist on the potential that, through infinitesimals, NSA offers in terms of discrete modelling for various areas of application. According to them, such potential means that NSA deserves full recognition.
In mathematics education too, diverse attempts have been made to develop non-standard approaches to the teaching of calculus. These were based either on Robinson’s construction (as those proposed by Keisler, 1976; and Henle & Kleinberg, 1979), or inspired from Nelson’s axiomatic approach (Deledicq & Diener, 1989). However, as pointed out by Hogdson (1994) in the synthesis of these realisations he presented at the ICME-7 Congress in Québec, none of these innovative constructions were sustainable in the long term. The marginal status of NSA certainly contributes to this, but also the fact that for achieving an efficient use of non-standard analysis, speaking of infinitesimals is not enough; one has to learn to manipulate new ideas and definitions, familiarise oneself with new modes of reasoning, build new references and intuitions, and develop new means of control.
Finally, this vignette illustrates two frequent phenomena in the history of science and mathematics:
- The fact that the integration of intuitive ideas into well founded theories may become accessible only decades and even centuries after these intuitions have been proved to be fruitful, thanks to other scientific advances. This was the case for the intuitive idea of infinitesimals thanks to the development of mathematical logic in the 20th century, but also for the intuitive idea of limit which is at the basis of standard analyses in the 19th century, as recalled at the beginning of this vignette;
- The fact also that several theorisations of the same domain of reality can coexist, offering fruitful and complementary perspectives in order to make sense of it and work on it. This is the case for standard and non-standard analysis, two different but complementary ways of approaching the field of functions and analysis, and to think about its relations with the real world.
We will end by pointing out that the construction presented here, that of NSA, is not the only possible one for giving a mathematical status to infinitesimals. Many different attempts have been made since the 18th century (cf. Borovik & Katz, 2012). Smooth infinitesimal analysis, developed from the ideas of F.W. Lawvere in the theory of categories is another recent construction: in it, an infinitesimal is defined as a number different from ![]() but whose square is
but whose square is ![]() (cf. Bell, 2008).
(cf. Bell, 2008).
References :
Bell, J.L. (2008). A primer of infinitesimal analysis, 2nd edition. Cambridge : Cambridge University Press.
Borovik, B. & Katz, M. (2012) Who Gave you the Cauchy-Weierstrass Tale? The Dual History of Rigorous Calculus. Foundations of Science 17, no. 3, 245-276.
Berkeley, G. (1734). The Analyst. http://www.maths.tcd.ie/pub/HistMath/People/Berkeley/Analyst/
Benoît, E., Callot, J.L., Diener, F., & Diener. M. (1981). Chasse au canard. Collectanea Mathematica, 32.1, 38-74.
http://collectanea.ub.edu/index.php/Collectanea/article/view/3537/4216
Deledicq A., & Diener, M. (1989). Leçons de calcul infinitésimal. Collection U. Paris : Armand Colin.
Diener, M., & Diener, F. (Eds.). (1995). Non standard analysis in practice. Berlin : Springer Verlag.
Henle, J.M., & Kleinberg, E.M. (1979). Infinitesimal Calculus. Cambridge : MIT Press.
Hodgson, B. (1994). Le calcul infinitésimal. In, D.F. Robitaille, D.H. Wheeler et C. Kieran (Eds.), Choix de conférence du 7e Congrès international sur l’enseignement des mathématiques (ICME-7), pp. 157-170. Québec : Presses de l’Université Laval.
Document.
Keisler, H.J. (1976). Elementary calculus : An infinitesimal approach. Boston : Prindle, Weber & Schmidt.
Lakatos, I. (1978): Cauchy and the continuum: the significance of nonstandard analysis for the history and philosophy of mathematics. Math. Intelligencer 1, no. 3, 151–161 (paper originally presented in 1966).
Lutz, R. & Goze, M. (1982). Non standard analysis : a practical guide with applications. Springer Lecture Notes in Mathematics, vol. 881. Berlin : Springer.
Marquis de l’Hôpital, G.F.A. (1696). Analyse des infiniment petits pour l’intelligence des lignes courbes. Paris : Imprimerie Royale.
Nelson, E. (1977). Internal set Theory, a new approach to NSA, Bull. Amer. Math. Soc., vol. 83, no 6, 1165-1198.
Robinson, A. (1996). Non standard analysis. North Holland, Amsterdam.
Skolem, Th. (1934). Über die Nicht-charakterisierbarkeit der Zahlenreihe mittels endlich oder abzählbar unendlich vieler Aussagen mit ausschliesslich Zahlenvariablen. Fundam. Math. 23, 150-161
![]()
![]() The scope of this calculus is huge: it is suitable for mechanical as well as geometric curves; radical signs are indifferent to it, and often convenient; it extends to so many indeterminate as one wants; comparing infinitely small quantities of all types is equally easy for it. From that arises an infinity of surprising discoveries regarding tangents both curved and straight, questions of maxima and minima, inflection points and cusps of curves, developed and caustics by reflection or refraction, etc., as explained in this book. (our translation)
The scope of this calculus is huge: it is suitable for mechanical as well as geometric curves; radical signs are indifferent to it, and often convenient; it extends to so many indeterminate as one wants; comparing infinitely small quantities of all types is equally easy for it. From that arises an infinity of surprising discoveries regarding tangents both curved and straight, questions of maxima and minima, inflection points and cusps of curves, developed and caustics by reflection or refraction, etc., as explained in this book. (our translation)
![]() ZFC stands for Zermelo-Fraenkel axioms plus the axiom of choice (see http://en.wikipedia.org/wiki/Zermelo–Fraenkel_set_theory).
ZFC stands for Zermelo-Fraenkel axioms plus the axiom of choice (see http://en.wikipedia.org/wiki/Zermelo–Fraenkel_set_theory).
![]() The axiom of idealization says that for any binary relation
The axiom of idealization says that for any binary relation ![]() which is classical (ie expressed without the use of the predicate
which is classical (ie expressed without the use of the predicate ![]() ), the following two statements are equivalent: (i) for any finite standard set
), the following two statements are equivalent: (i) for any finite standard set ![]() , there exists an
, there exists an ![]() such that for any
such that for any ![]() of
of ![]() ,
, ![]() ; (ii) there is an
; (ii) there is an ![]() such that, for any
such that, for any ![]() standard,
standard, ![]() .
.
The axiom of standardization says that for any property ![]() and any standard set
and any standard set ![]() , there is a standard part
, there is a standard part ![]() of
of ![]() whose standard elements are exactly the elements of
whose standard elements are exactly the elements of ![]() that satisfy
that satisfy ![]() . This axiom works whether
. This axiom works whether ![]() is a classical property or not.
is a classical property or not.
The axiom of transfer says that for any classical property ![]() ,
, ![]() is true for all
is true for all ![]() if and only if
if and only if ![]() is true for all
is true for all ![]() standard.
standard.
![]() Apply the axiom of transfer with the property
Apply the axiom of transfer with the property ![]() :
: ![]()
![]() In the first case, the axiom of idealization is applied to the binary relation
In the first case, the axiom of idealization is applied to the binary relation ![]() in
in ![]() ; in the second case, it is applied to the binary relation
; in the second case, it is applied to the binary relation ![]() in the infinite set considered.
in the infinite set considered.
![]() In this table, all objects:
In this table, all objects: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are supposed standard.
are supposed standard.
![]() In this statement too,
In this statement too, ![]() ,
, ![]() ,
, ![]()
![]() are supposed standard.
are supposed standard.

Nice post. Note that they are “Riemann sums”, not “Cauchy sums”. Also, there is a phrase in French: ” et nous invitons le lecteur à compléter lorsque possible les cases des deux tableaux suivants” that seems to be out of place.
Thanks Miklail for signaling this point. The first version of the vignette was in French. It has been corrected.
Also, Henle’s name is misspelled (“Heinle”).
Your observation that in smooth infinitesimal analysis of Lawvere (and others) “an infinitesimal is defined as a number different from 0 but whose square is 0” is not entirely correct. These numbers cannot be shown to be different from zero. As you point out, the background logic is intuitionistic, so this does not allow one to conclude that they are zero.