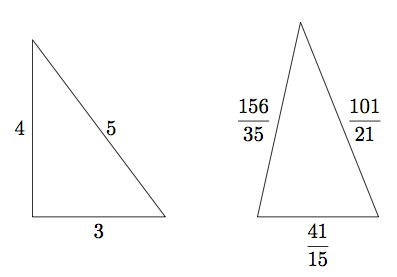 Originating author is William Mc Callum.
Originating author is William Mc Callum.
If two triangles have the same area and the same perimeter, are they necessarily congruent? It turns out that the answer is no. For example, the triangle with sides ![]()
![]() and
and ![]() has the same area and perimeter as the triangle with sides
has the same area and perimeter as the triangle with sides ![]() ,
, ![]() , and
, and ![]() .
.
Both triangles have perimeter ![]() :
:
![]()
Amazingly, the two triangles also have the same area. The right triangle has area ![]() . To find the area of the other triangle, we use Heron’s formula, which states that the area
. To find the area of the other triangle, we use Heron’s formula, which states that the area ![]() of a triangle with side lengths
of a triangle with side lengths ![]() ,
, ![]() , and
, and ![]() , is given by
, is given by
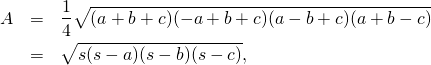
where ![]() is the semiperimeter of the triangle. A quick calculation using this formula shows that the area of the second triangle is also 6.
is the semiperimeter of the triangle. A quick calculation using this formula shows that the area of the second triangle is also 6.
The space of triangles
How do we find examples like this? The secret is to find the right way of representing the space of all triangles. There are many possible ways to do this. One way is to represent a triangle by the triple ![]() consisting of its three side lengths in some order. In this way we represent a triangle by a point in
consisting of its three side lengths in some order. In this way we represent a triangle by a point in ![]() space. Not every point corresponds to a triangle; for example, all the coordinates must be positive. Can you think of other restrictions?
space. Not every point corresponds to a triangle; for example, all the coordinates must be positive. Can you think of other restrictions?
There’s another way of putting coordinates on the space of triangles using angles instead of lengths. Every triangle has an inscribed circle, and the radius ![]() of the circle has a simple relationship with the area
of the circle has a simple relationship with the area ![]() and semiperimeter
and semiperimeter ![]() , namely
, namely
![]()
To see why this is true, drop perpendiculars from the center of the circle to the sides of the triangle, as in the left diagram in Figure 2. These perpendiculars form the altitudes of 3 smaller triangles with bases on the sides of the big triangle and vertices at the center of the inscribed circle. Adding up the areas of these triangles we get ![]() .
.
-

- Figure 2: Parameterizing the space of triangles
This equation tells us that if two triangles have the same area and same semiperimeter, then the radii of their inscribed circles are also the same. So if we are looking for two such triangles we will find them amongst all triangles inscribed around a fixed circle. Instead of using lengths to describe these triangles, we will use the angles formed by the three radii at the center of incircle, as in the right diagram in Figure 2.
Parameterizing triangles with constant area and perimeter
Inside the space of triangles we can find curves corresponding to a whole family of triangles with the same values of ![]() and
and ![]() .
.
First, we express ![]() in terms of the angles
in terms of the angles ![]() ,
, ![]() , and
, and ![]() and the radius
and the radius ![]() of the incircle, as follows. The radii and the lines from the vertices to the incenter break the triangle into six right triangles. Because the lines from the vertices to the center bisect the angles of the big triangle, these right triangles occur in congruent pairs. Taking one base length from each pair and adding, we get
of the incircle, as follows. The radii and the lines from the vertices to the incenter break the triangle into six right triangles. Because the lines from the vertices to the center bisect the angles of the big triangle, these right triangles occur in congruent pairs. Taking one base length from each pair and adding, we get
![]()
This equation and ![]() together tell us that if the area
together tell us that if the area ![]() and semiperimeter
and semiperimeter ![]() are constant, then so is the sum of the tangents:
are constant, then so is the sum of the tangents:
(1) ![]()
Second, we translate this condition into an equation defining a curve in the plane. Let ![]() ,
, ![]() , and
, and ![]() . Since
. Since ![]() , we have
, we have
![]()
so
![]()
Then, if ![]() is the constant
is the constant ![]() , equation (1) becomes for fixed
, equation (1) becomes for fixed ![]() , the equation
, the equation
(2) ![]()
(3) ![]()
Every triangle with area ![]() and semiperimeter
and semiperimeter ![]() determines a point on this curve, and every point on the curve in a certain region of the plane corresponds to a triangle. The region corresponds to angles that actually work in Figure 2, namely angles satisfying
determines a point on this curve, and every point on the curve in a certain region of the plane corresponds to a triangle. The region corresponds to angles that actually work in Figure 2, namely angles satisfying ![]() and
and ![]() , which corresponds to the region
, which corresponds to the region ![]() ,
, ![]() and
and ![]() (since
(since ![]() ).
).
The following figure shows this curve for ![]() , the value corresponding to the triangle with sides 3, 4, and 5. Every point on the component of this curve in the positive quadrant corresponds to a triangle; the side lengths of the triangle are
, the value corresponding to the triangle with sides 3, 4, and 5. Every point on the component of this curve in the positive quadrant corresponds to a triangle; the side lengths of the triangle are ![]() ,
, ![]() , and
, and ![]() . In particular, the points
. In particular, the points ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() all correspond to the triangle with sides
all correspond to the triangle with sides ![]() ,
, ![]() , and
, and ![]() , with the sides taken in different orders. This figure is interactive: see what happens for some other points on the curve or some other values for the area and perimeter!
, with the sides taken in different orders. This figure is interactive: see what happens for some other points on the curve or some other values for the area and perimeter!
Finding points on the curve
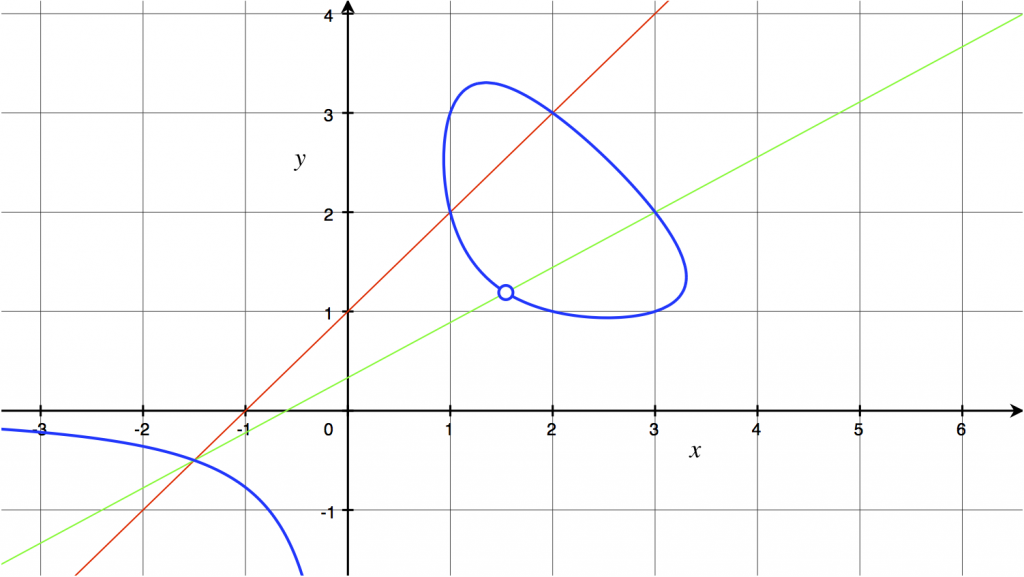
Figure 3: Curve parameterizing triangles of perimeter 12 and area 6.
Because the curve in Figure 3 is defined by an equation of degree 3, we can find points on it using the method of tangents and secants. Two points on the curve determine a secant which cuts the curve in one more point; finding the point amounts to solving a cubic equation in ![]() , two of whose roots are already known. Since we already have 6 points on the curve, there are lots of possibilities for secants, and generating more points generates more possibilities. In fact, the curve has infinitely many points with rational coordinates. The two-secant procedure illustrated in Figure 3 leads to the point
, two of whose roots are already known. Since we already have 6 points on the curve, there are lots of possibilities for secants, and generating more points generates more possibilities. In fact, the curve has infinitely many points with rational coordinates. The two-secant procedure illustrated in Figure 3 leads to the point ![]() (marked with a circle), which corresponds to the triangle with sides
(marked with a circle), which corresponds to the triangle with sides ![]() ,
, ![]() , and
, and ![]() .
.
The secant procedure works for any cubic curve in the plane; such curves are called elliptic curves (not because the curves are themselves ellipses, but because they arise in the study of a certain class of complex functions called elliptic functions). The secant procedure allows one to define a group structure on the set of rational points on a elliptic curves (that is, points whose coordinates are rational numbers).
The study of elliptic curves is a central area of research in number theory, with applications to the cryptographic schemes behind secure financial transactions on the web. Elliptic curves played a central role in the proof of Fermat’s Last Theorem.
The story described in this article shows the remarkable unity of mathematics, starting as it does in high school and ending in research. Along the way we encountered a fundamental idea in modern mathematics: the idea of solving a problem about a particular type of object (triangles with area 6 and perimeter 12, for example) by situating the object in a more general space (the space of all triangles) and finding the right way of parameterizing that space.

Beautiful stuff. A related article is Rosenberg, Spillane, Wulf, “Heron Triangles and Moduli Spaces,” The Mathematics Teacher 101 (2008), 656-663. The article contains insightful Geometer’s Sketchpad pictures created by HS teacher extraordinaire Dan Wulf. If you contact Dan, he’ll send you the Sketchpad files, which include great animations of all triangles of a fixed area and perimeter.
This article was in fact the inspiration for this piece, thanks Steve for mentioning it. I’m still trying to figure out how to embed Sketchpad or Geogebra animations in a WordPress blog.
dear sir!
i am a mathematical student at Royal University of Phnom Penh!i am interested in klein project serously.i think that this program is a guideline for us to be a good mathematical teacher. i know,if we want to be good at mathematics,it is very hard. However,i want to tell u that i really like and love math so much. But , sometimes i don’t have enough mathematical document to search for,for example math exercise book and i also don’t have enough time to reading book too because my lifestyle thannks for your presentation at my university.
sincerely from me
Pak So Kreth
Awesome detail about using Hero’s formula and cool explanations on the Elliptic Curves. Very rare to find such blogs online.
Excellent article, in the same spirit as “Roots to Research,” by Judith and Paul Sally. There should be more material like this in the courses that prepare secondary teachers.
Pingback: Il perimetro e l’space determinano un triangolo? - Ingegneria
Pingback: Can You Hear the Shape of a Black Hole? - 3 Quarks Daily