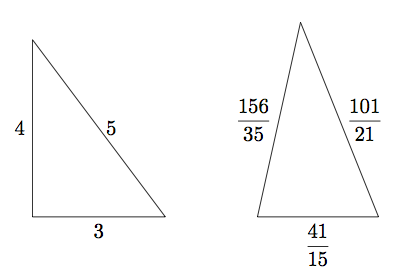如果两个三角形有相同的面积和周长,那么这两个三角形是全等的么?答案是否定的。例如,三边长分别为 $3$、$4$、$5$ 的三角形和三边长分别为 $41/15$、 $101/21$、 $156/35$ 的三角形有相同的面积和周长。两个三角形周长都是 $12$
\begin{displaymath}
3 + 4 + 5 =12, \quad \hbox{and} \quad \frac{41}{15} + \frac{101}{21} + \frac{156}{35} = \frac{287 +
505 + 468}{105} = \frac{1260}{105} = 12.
\end{displaymath}
令人惊讶地是,两个三角形也有相同的面积。右边的三角形面积为 $\frac{1}{2} 4 \cdot 3 = 6$ 。为了计算另一个三角形的面积,我们使用海伦公式,边长为 $a$,$b$,$c$ 的三角形的面积 $A$ 由下列公式给出:
\begin{eqnarray*}
A &=& \frac{1}{4}\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}\\
&=& \sqrt{s(s-a)(s-b)(s-c)},
\end{eqnarray*}
这里 $s = \frac12(a+b+c)$ 是三角形周长的一半,通过这个公式的计算我们可以发现第二个三角形的面积也是 $6$ 。
三角形空间
我们如何发现这类例子呢?关键是找到合适的方式来表示所有这些三角形。这里有很多可能的方法,其中一种就是通过构成三角形三条边的一定顺序的三维数组 $(a, b, c)$ 来表示一来表示一个三角形。通过这种方式,我们用一个三维的点对应一个三角形。但是,并不是所有的点都有对应的三角形,例如:能对应三角形的点必须坐标都是正的。你还能想到其他的限制么?另一种方法是通过使用角而不是边将坐标用于刻画所有这些三角形构成的空间。每个三角形有一个内切圆,圆的半径 与三角形的面积 和半周长 有个简单的关系,即 $A = rs$.
为了证明这个结论,从圆心向三角形的三边作垂线,如图2左边的图形所示。这些垂线分别是以大三角形的三边为底边、以内切圆的圆心为顶点的三个小三角形的高。把这些小三角形的面积加起来我们可以得到 $A=rs$ 。
\begin{tikzpicture}
\begin{scope}
\draw (0,0) — (101/21,0) — (1691/1515,252/101) — cycle;
\draw (54/35,1) circle (1);
\draw[gray] (54/35,0) — (54/35,1);
\draw[gray] (54/35,1) — (0.630034153,1.40835547);
\draw[gray] (54/35,1) — (2.10264, 1.82864);
\draw (54/35,1) — (0,0);
\draw (54/35,1) — (101/21,0);
\draw (54/35,1) — (1691/1515,252/101);
\node [below] at (54/35,0) {$c$};
\node [left] at (0.630034153,1.40835547) {$a$};
\node [right,above] at (2.20264, 1.82864) {$b$};
\end{scope}
\begin{scope}[xshift=2in]
\draw (0,0) — (101/21,0) — (1691/1515,252/101) — cycle;
\draw (54/35,1) circle (1);
\draw (54/35,0) — (54/35,1);
\draw(54/35,1) — (0.630034153,1.40835547);
\draw (54/35,1) — (2.10264, 1.82864);
\node [below] at (54/35,0) {$c$};
\node [left]at (0.630034153,1.40835547) {$a$};
\node [right,above] at (2.20264, 1.82864) {$b$};
\node [above] at (1.5,1) {$\gamma$};
\node [left] at (1.5,.8) {$\beta$};
\node [right] at (1.5,1) {$\alpha$};
\end{scope}
\end{tikzpicture}图2:三角形空间的参数表示这个公式告诉我们如果两个三角形有相等的面积和半周长,它们的内切圆的半径也相等。因此,如果我们要找两个面积和周长分别相等的三角形,我们可以在一个固定的圆的所有外切三角形中寻找。这样我们可以使用内切圆的三条半径所夹的角而非长度来刻画三角形,如图2右边的图形所示。
用固定的周长和面积建立参数表示三角形
在三角形的空间内,我们可以找到曲线族来对应具有相同变量 $A$ 和 $s$ 的一簇三角形。首先,我们通过角 $\alpha$, $\beta$, 以及圆的半径来表示半周长 $s$ (如下所示)。半径以及从顶点到圆心的线将大三角形分成六个直角三角形。由于从顶点到圆心的线分别平分大三角形对应的角,这些直角三角形分为全等的三组。从每一组里选择一边加起来,我们得到
$$
s=r (\tan \frac{\alpha}{2} + \tan \frac{\beta}{2} + \tan
\frac{\gamma}{2}).
$$
这个等式联合 $A = rs$ ,我们可以知道如果面积 $A$ 和半周长 是固定的,那么正切值的和也是一个定值。
\begin{equation}\label{eq:fracs2a-=-fracsr} \tan \frac{\alpha}{2} + \tan \frac{\beta}{2} + \tan
\frac{\gamma}{2} = \frac{s^2}{A}.
\end{equation}
接着,我们把这个条件转化为定义平面内一条曲线的一个等式。令
$$x = \tan (\alpha/2) ,$$ $$y = \tan(\beta/2),$$ $$z = \tan(\gamma/2).$$
因为 $\alpha+\beta+\gamma = 2\pi$ , 我们有
\begin{equation*}
\frac{\gamma}{2} = {\pi} – \frac{\alpha}{2} – \frac{\beta}{2},
\end{equation*}
因此,
\begin{equation*}
z = \tan \left(
\frac{\gamma}{2}
\right)= \tan\left({\pi} – \frac{\alpha}{2} – \frac{\beta}{2}\right)
= – \tan\left(\frac{\alpha}{2} + \frac{\beta}{2}\right) = – \frac{x +
y}{1-xy}.
\end{equation*}
于是,如果设 等于定值 $s^2/A$,等式 (??) 可以化为关于 的等式
\begin{equation}\label{eq:x-+-y}
x + y – \frac{x + y}{1-xy} = k,
\end{equation}
我们也可以写成
\begin{equation}
\label{eq:rewrite}
x^2y+xy^2 = kxy – k.
\end{equation}
每一个面积为 $A$ 、半周长为 $s$ 的三角形决定了曲线上的一个点,同样在一定的平面区域内曲线上的每个点都对应了一个三角形。该区域对应如图 $2$ 中所示的三角形,即满足 $\alpha + \beta + \gamma = 2\pi$ 和 $0 < \alpha, \beta, \gamma < \pi$ 的三角形对应了 $x > 0$, $y > 0$, $xy > 1$ ($z > 0$) 的区域。
图3所示的曲线 $k=6$ ,对应三边长为 $3, 4, 5$ 的三角形。在第一象限的曲线上的每一个点对应了一个三角形,三角形的三边分别为 $a = x+ y$, $b = y + z$, $c = z + x$ 。值值得一提地是,点 $(1,2)$, $(2,1)$, $(2, 3)$, $(3, 2)$, $(1, 3)$, $(3, 1)$ 都对应了三边长为 $3, 4, 5$ 的三角形,三边长的顺序不同。
找到曲线上的点
因为图3中的曲线是由一个三次方程决定的,我们可以通过切线和割线来找到曲线上的点。曲线上的两个点决定了一条割线,这条割线将交曲线于第三个点。我们可以找到点的数量来解决关于 $x$ 的、已知两根的三次方程。由于我们已知曲线上的 $6$ 个点,那么割线的可能性会有很多种,由此产生更多的点来产生更多的可能性。事实上,曲线上有无穷多个有理点。图3中的两条割线引出了一个新的点$(54/35, 25/21)$ (用空心圆标注的),这个点对应了三边长为 $41/15$、 $101/21$、$156/35$ 的三角形。
寻找割线的过程对于平面内任何三次曲线都适用。这些曲线称之为椭圆曲线(并不是因为曲线本身是椭圆的,而是因为它们出现在一类称之为椭圆函数的复杂函数的研究中)。通过割线的操作,可以定义建立在椭圆曲线上有理点集合上的群结构。(也就是说,这些点的坐标都是有理数)
椭圆曲线的研究是数论研究的一个重要领域,它在网上金钱交易安全加密设计上也有应用。同时,椭圆曲线在费马大定理的证明中也起到了重要作用。
这篇文章描述的故事揭示了数学非同一般的一致性,它体现在来源于中学的一个数学问题最后演变成数学前沿的研究问题。在这个过程中,我们邂逅了数学的一个基本思想:为了解决一个关于特定对象的问题(例如:决定面积为6,周长为12的所有三角形),我们可以将该对象置于更一般的情形(所有满足条件的三角形空间),并且找到了利用参数表示这些三角形的正确方法。