 Autor original: Christiane Rousseau.
Autor original: Christiane Rousseau.
¿Cuál es el empaquetamiento de esferas más denso? Kepler conjeturó que era el que se puede ver en las naranjas en cualquier frutería, denominado red cúbica centrada en las caras (Figura 1, a la izquierda). En el Congreso Internacional de Matemáticos de 1900, David Hilbert impartió una conferencia muy famosa en la cual enunció 23 problemas que tendráin gran relevancia para el avance de las matemáticas en el siglo XX. El problema del empaquetamiento de esferas más denso, también conocido como conjetura de Kepler, es parte del 18º problema de Hilbert. La conjetura de Kepler fue probada en 1998 por Thomas Hales y los detalles de la demostración se publicaron en 2006.
1. ¿Cómo lidiar con problemas de este tipo?
Se consideran diferentes configuraciones de esferas (bolas sólidas) iguales en el espacio y, en cada caso, se calcula la densidad del empaquetado, es decir, la fracción del volumen total que está ocupada por las esferas. Denotaremos por ![]() a la densidad máxima de los empaquetamientos en dimensión
a la densidad máxima de los empaquetamientos en dimensión ![]() . Por supuesto, esta densidad depende de la forma de la región del espacio en que se esté trabajando. Para evitar esto, consideraremos regiones muy grandes, de manera que el efecto de los límites sea insignificante. Kepler conjeturó en 1611 que la configuración más densa es la que se observa en las naranjas en la frutería. Entonces, ¿por qué se tardó tanto tiempo en probar esta conjetura? El problema es que existe un número infinito de posibles configuraciones de esferas.Cada vez que se toma una configuración tiene que probarse que su densidad es menor o igual que la observada en la frutería. El problema es que solo podemos describir un número finito de configuraciones e, incluso con una única configuración, el cálculo de su densidad puede ser difícil o imposible si la configuración no es periódica.
. Por supuesto, esta densidad depende de la forma de la región del espacio en que se esté trabajando. Para evitar esto, consideraremos regiones muy grandes, de manera que el efecto de los límites sea insignificante. Kepler conjeturó en 1611 que la configuración más densa es la que se observa en las naranjas en la frutería. Entonces, ¿por qué se tardó tanto tiempo en probar esta conjetura? El problema es que existe un número infinito de posibles configuraciones de esferas.Cada vez que se toma una configuración tiene que probarse que su densidad es menor o igual que la observada en la frutería. El problema es que solo podemos describir un número finito de configuraciones e, incluso con una única configuración, el cálculo de su densidad puede ser difícil o imposible si la configuración no es periódica.
El problema del empaquetado más denso de bolas sólidas existe en cualquier dimensión. En 1890 fue resuelto para bolas sólidas ![]() -dimensionales. Empaquetar bolas en dimensiones más altas tiene aplicaciones, por ejemplo, en códigos correctores de errores.
-dimensionales. Empaquetar bolas en dimensiones más altas tiene aplicaciones, por ejemplo, en códigos correctores de errores.
Ya en dimensión ![]() se encuentran estas dos dificultades: no se pueden enumerar todas las posibles configuraciones y, además, algunas de ellas pueden no ser periódicas. Mostraremos cómo tratar estas dificultades y probaremos que el empaquetamiento de la Figura 2(b) es el más denso entre todas las posibles configuraciones. Explicaremos también las dificultades de generalizar la demostración al caso
se encuentran estas dos dificultades: no se pueden enumerar todas las posibles configuraciones y, además, algunas de ellas pueden no ser periódicas. Mostraremos cómo tratar estas dificultades y probaremos que el empaquetamiento de la Figura 2(b) es el más denso entre todas las posibles configuraciones. Explicaremos también las dificultades de generalizar la demostración al caso ![]() -dimensional y concluiremos con algunos comentarios en dimensiones más altas.
-dimensional y concluiremos con algunos comentarios en dimensiones más altas.
2. El caso ![]() -dimensional.
-dimensional.
Si consideramos las dos disposiciones de discos de la Figura 2, resulta fácil calcular en el caso (a) la fracción de cada cuadrado y en el caso (b) la fracción de cada triángulo que están cubiertas por porciones de discos. Se puede ver que en el segundo caso se obtiene una mayor densidad. De hecho, los discos en (a) tienen una densidad de ![]() mientras que en (b) es de
mientras que en (b) es de
![]()
Siempre que se considere un empaquetamiento periódico se tiene que es menos denso que el de la Figura 2(b).
Pero, ¿cómo se prueba esto mismo para cualquier empaquetamiento?
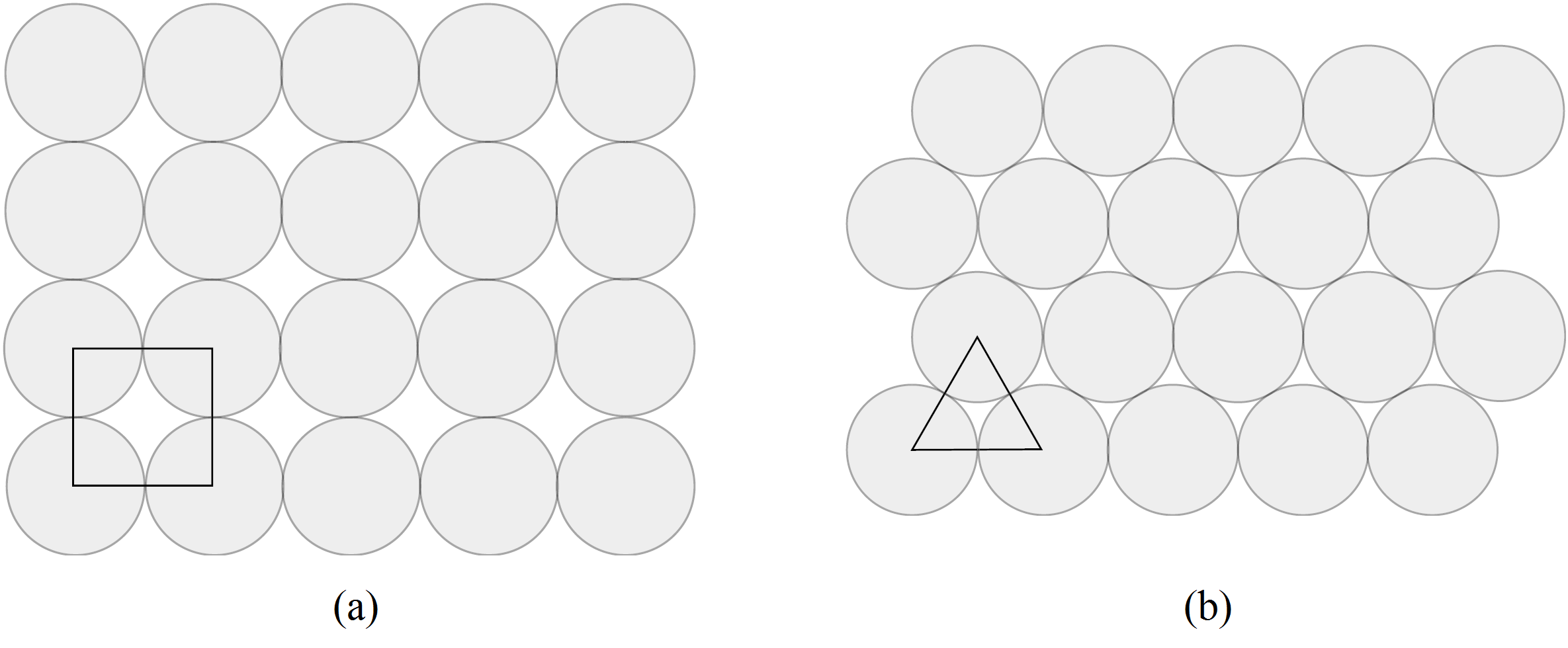
He aquí una idea inteligente, que se remonta al matemático noruego Axel Thue en 1890. Se divide el plano en regiones locales y se prueba que, en cada región, la densidad es menor o igual que ![]() . Estudiemos ahora la Figura 3. En ella aparecen tres discos que no pueden estar más cerca uno de otro. Ahora miremos el triángulo con vértices en los centros de los discos. Dentro del triángulo hay una pequeña región que no está cubierta por los discos. Si agrandamos los discos con un factor de aumento
. Estudiemos ahora la Figura 3. En ella aparecen tres discos que no pueden estar más cerca uno de otro. Ahora miremos el triángulo con vértices en los centros de los discos. Dentro del triángulo hay una pequeña región que no está cubierta por los discos. Si agrandamos los discos con un factor de aumento ![]() entonces los discos cubren totalmente el triángulo y este factor
entonces los discos cubren totalmente el triángulo y este factor ![]() es el mínimo con el que se consigue cubrir el triángulo con los discos aumentados.
es el mínimo con el que se consigue cubrir el triángulo con los discos aumentados.
Usaremos este truco para dividir el plano en regiones adecuadas. Consideramos un empaquetamiento de discos de radio ![]() en el plano. Insertamos cada uno de los discos en otro disco con el mismo centro y radio
en el plano. Insertamos cada uno de los discos en otro disco con el mismo centro y radio ![]() , que llamaremos disco grande. Ahora podemos definir nuestras tres regiones. La primera región es el conjunto complementario a la unión de los discos grandes. Obviamente, la densidad de eta región es
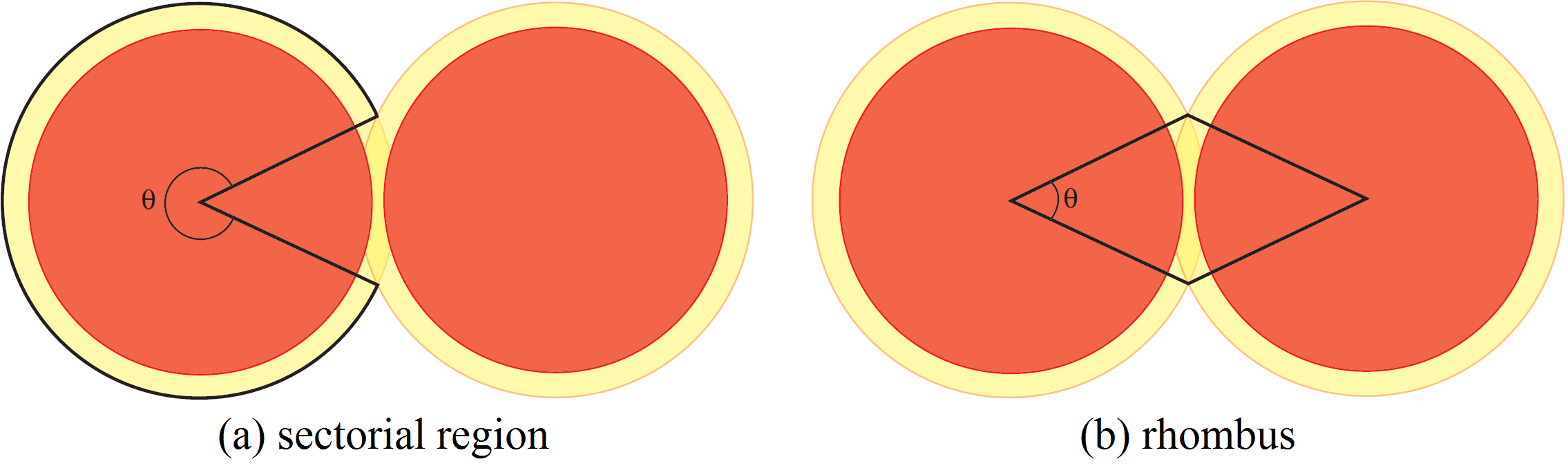
, que llamaremos disco grande. Ahora podemos definir nuestras tres regiones. La primera región es el conjunto complementario a la unión de los discos grandes. Obviamente, la densidad de eta región es ![]() . Dependiendo de la distancia entre los centros, los discos grandes pueden o no superponerse. Cuando los dicos grandes se superponen, sus correspondientes círculos frontera tienen puntos de intersección. Uniendo estos puntos con los centros de los discos conseguimos dividir los discos grandes en sectores. Hay dos tipos de sectores:
. Dependiendo de la distancia entre los centros, los discos grandes pueden o no superponerse. Cuando los dicos grandes se superponen, sus correspondientes círculos frontera tienen puntos de intersección. Uniendo estos puntos con los centros de los discos conseguimos dividir los discos grandes en sectores. Hay dos tipos de sectores:
-
sectores en los que los discos grandes no se superponen (ver Figura 4 (a)). En estos sectores la densidad es
![Rendered by QuickLaTeX.com \[\frac{1}{c^2}=\frac{3}{4};\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-7a5b412bf3acabb8882fdc0cf1c6347e_l3.png)
-
sectores en los que los discos grandes se superponen como en la Figura 4 (b). Consideramos estos sectores por parejas, como en la figura. La unión de dos sectores es un rombo y solo necesitamos considerar la densidad dentro de este rombo. Como la distancia entre los centros de los discos es al menos
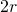 debido a que los discos no se superponen, un sencillo cálculo muestra que el ángulo máximo de los sectores es
debido a que los discos no se superponen, un sencillo cálculo muestra que el ángulo máximo de los sectores es 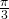 . Sea
. Sea 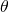 el ángulo del sector. La densidad en el interior del rombo depende de
el ángulo del sector. La densidad en el interior del rombo depende de 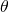 : viene dado por el cociente entre las áreas de los dos sectores de los discos y el áera del rombo. Cada sector de un disco tiene área
: viene dado por el cociente entre las áreas de los dos sectores de los discos y el áera del rombo. Cada sector de un disco tiene área 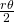 . Por tanto, el área cubierta por los discos en el interior del rombo es
. Por tanto, el área cubierta por los discos en el interior del rombo es 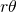 . El área de un rombo de lado
. El área de un rombo de lado 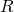 y ángulo
y ángulo 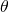 se calcula descomponiendo el rombo en triángulos y es igual a
se calcula descomponiendo el rombo en triángulos y es igual a 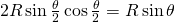 . Por tanto, la densidad es
. Por tanto, la densidad es
![Rendered by QuickLaTeX.com \[\mu(\theta)=\frac{r^2\theta}{R^2\sin\theta}=\frac{3\theta}{4\sin\theta}.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-90f24f10ca630f0e9d01b943b639c102_l3.png)
Basta por tanto con estudiar la función
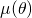 on
on ![Rendered by QuickLaTeX.com [0,\frac{\pi}3]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-97108dd255a2234a8ad4dd9ed1cb498f_l3.png) y ver que alcanza su máximo en
y ver que alcanza su máximo en 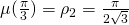 . De hecho,
. De hecho, 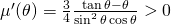 ya que
ya que 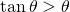 .
.
Esta demostración es extremadamente elgante. Examinemos en detalle algunas de sus características. La mejor densidad es ![]() . Es también localmente la mejor densidad en cada una de las regiones del plano que hemos considerado.
. Es también localmente la mejor densidad en cada una de las regiones del plano que hemos considerado.
Hay otra manera de dividir el plano en regiones: es el diagrama de Voronoi del conjunto de centros de los discos. Si consideramos un conjunto ![]() de puntos en el plano el diagrama de Voronoi de
de puntos en el plano el diagrama de Voronoi de ![]() es la partición del plano en regiones, cada una asociada a un punto
es la partición del plano en regiones, cada una asociada a un punto ![]() de
de ![]() , de manera que la región correspondiente a un determinado punto
, de manera que la región correspondiente a un determinado punto ![]() es el conjunto de puntos del plano que están más cerca de
es el conjunto de puntos del plano que están más cerca de ![]() que de cualquier otro punto
que de cualquier otro punto ![]() de
de ![]() . Estas regiones se denominan celdas de Voronoi. Dado que la mediatriz del segmento
. Estas regiones se denominan celdas de Voronoi. Dado que la mediatriz del segmento ![]() es el lugar geométrico de los puntos que equidistan de
es el lugar geométrico de los puntos que equidistan de ![]() y de
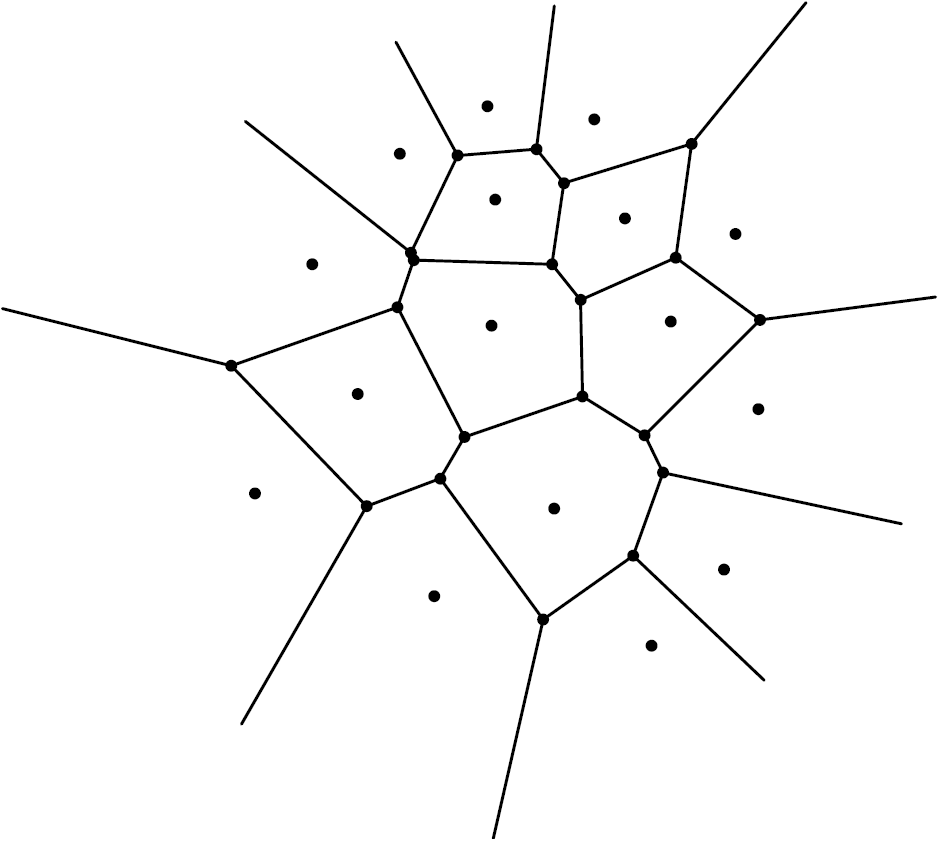
y de ![]() , no es sorprendente que el diagrama de Voronoi de un conjunto de puntos se parezca a la Figura 5, con un lado común entre cada par de celdas de Voronoi adyacentes dado por el segmento de la medriatriz de los puntos de
, no es sorprendente que el diagrama de Voronoi de un conjunto de puntos se parezca a la Figura 5, con un lado común entre cada par de celdas de Voronoi adyacentes dado por el segmento de la medriatriz de los puntos de ![]() asociados a las celdas.
asociados a las celdas.
Si tenemos un empaquetamiento de discos en el plano, es natural considerar el diagrama de Voronoi de los centros de los discos. Volvamos a los ejemplos de la Figura 2. A la izquierda, las celdas de Voronoi son cuadrados; a la derecha son hexágonos y la densidad de cada disco en su celda de Voronin hexagonal es exactamente ![]() . Notar que si rodeamos un disco con discos del mismo radio que no se suiperpongan, entonces la celda de Voronin de área mínima es el hexágono circunsctrito.
. Notar que si rodeamos un disco con discos del mismo radio que no se suiperpongan, entonces la celda de Voronin de área mínima es el hexágono circunsctrito.
3. El caso tridimensional.
3.1. La dificultad del problema.
Es natural tratar de generalizar esta idea al caso tridimensional. El diagrama de Voronoi se puede definir de la misma manera. Sus celdas cerradas son poliedors convexos. Si rodeamos una esfera con esferas tangentes podemos colocar ![]() . Pero en contraposición al caso del plano, aún queda espacio libre alrededor de la primera esfera. Podemos intentar movernos alrededor de las
. Pero en contraposición al caso del plano, aún queda espacio libre alrededor de la primera esfera. Podemos intentar movernos alrededor de las ![]() esferas tangentes y ver si queda lugar para una decimotercera. Thomas Hales demostró que esto no es posible. Pero existen muchas formas diferentes y no equivalentes de colocar
esferas tangentes y ver si queda lugar para una decimotercera. Thomas Hales demostró que esto no es posible. Pero existen muchas formas diferentes y no equivalentes de colocar ![]() esferas tangentes a una dada y que producen celdas de Voronoi de diferente volumen. La configuración óptima para minimizar el volumen de la celda de Voronoi es que las
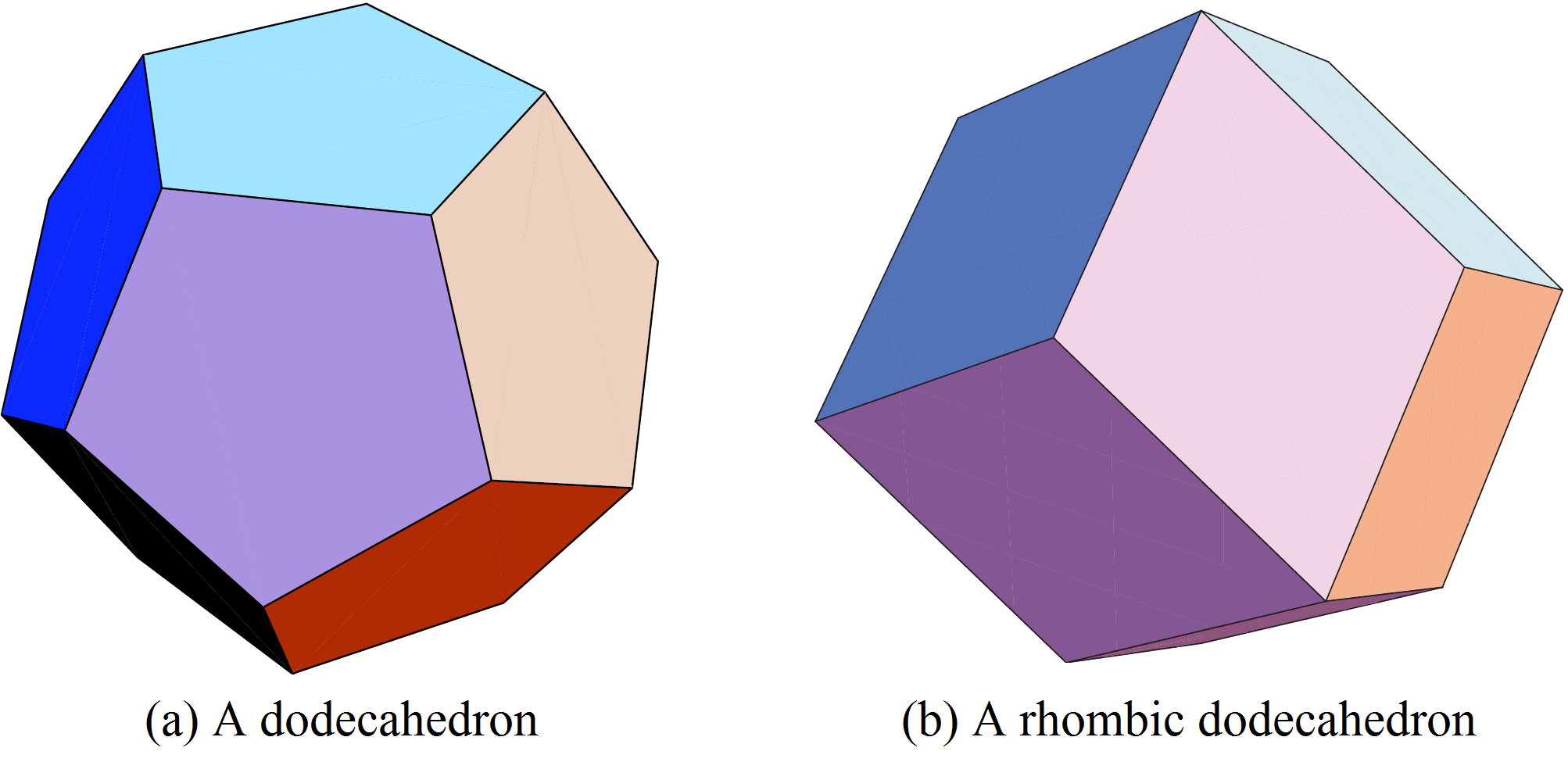
esferas tangentes a una dada y que producen celdas de Voronoi de diferente volumen. La configuración óptima para minimizar el volumen de la celda de Voronoi es que las ![]() esferas sean tangentes a la esfera original en los vértices del dodecaedro inscrito (ver Figura 6 (a)). Esto fue conjeturado por Fejer Tóth en la década de 1940 y demostrado por un estudiante universitario, Sean McLaughlin, in 1999.
esferas sean tangentes a la esfera original en los vértices del dodecaedro inscrito (ver Figura 6 (a)). Esto fue conjeturado por Fejer Tóth en la década de 1940 y demostrado por un estudiante universitario, Sean McLaughlin, in 1999.
Por tanto, la celda de Voronoi de una esfera dada es un dodecaedro circunscrito a la esfera. Es posibla calcular la densidad de la esfera dentro de su celda de Voronoi y ¡es inferior a la densidad del empaquetado de las naranjas en la frutería! ¿Podemos hacerlo mejor?
¡No!
Porque es imposible llenar el espacio con dodecaedros que no se superpongan: necesariamente obtenemos espacio vacío entre ellos. Por tanto, el caso tridimensional es mucho más difícil que el de dimensión dos porque la solución local óptima no coincide con la solución global óptima.
Para la solución óptima cuya geometría estudiaremos en la siguiente sección, los centros de las esferas se localizan en los puntos de una red cúbica centrada en las caras. Las correspondientes celdas de Voronoi son dodecaedros rómbicos (ver Figura 6 (b)).
Los dodecaedros rómbicos teselan el espacio de manera regular y estas teselaciones se han observado en cristalografía.
La demostración de la optimidad de este empaquetamiento fue conseguida por Thomas Hales con la ayuda de su estudiante Samuel Ferguson en 1998 (la demostración completa se publicó en 2006). La demostración, asistida por ordenador, es verdaderamente brillante. Aunque no se puede imitar la prueba del caso de dimensión dos, la filosofía es la misma: la demostración consiste en descomponer el espacio en regiones de un número finito de tipos y calcular la densidad en cada tipo de región. El (enorme) programa está disponible en la red para aquel que desee estudiarlo o comprobarlo.
3.2. La geometría del empaquetado óptimo.
Imagine el lector una teselación del espacio tridimensional mediante cubos. En cada cubo colocamos una esfera centrada en cada vértice y una esfera centrada en el centro de cada cara como en
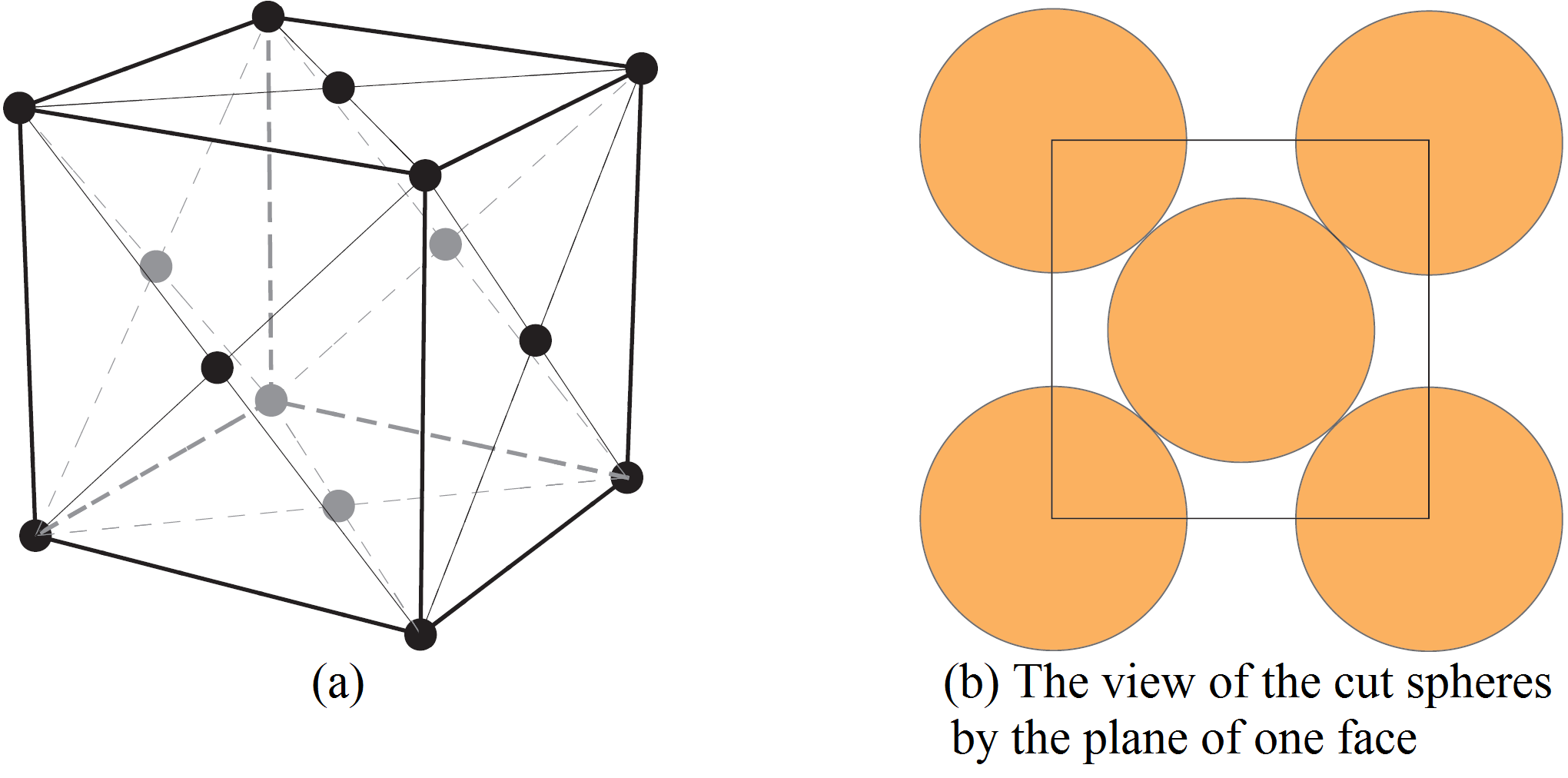
Tomamos el radio de las esferas tan grande como sea posible sin que las esferas se intersequen. Si ![]() es la longitud de arista de los cubos, es claro de la Figura 7 (b) que el radio de las esferas debe ser
es la longitud de arista de los cubos, es claro de la Figura 7 (b) que el radio de las esferas debe ser ![]() . Calculemos la dendidad del empaquetado. Un octavo del volumen de cada esfera centrada en un vértice está dentro del cubo. Como cada cubo tiene ocho vértices, se obtiene el volumen de una esfera completa. La mitad de cada esfera centrada en una cara está dentro del cubo. Como cada cubo tiene seis caras, se obtiene el volumen equivalente a tres esferas. Por tanto, la densidad es el volumen de cuatro esferas dividido entre el volumen del cubo. El volumen de cada esfera es
. Calculemos la dendidad del empaquetado. Un octavo del volumen de cada esfera centrada en un vértice está dentro del cubo. Como cada cubo tiene ocho vértices, se obtiene el volumen de una esfera completa. La mitad de cada esfera centrada en una cara está dentro del cubo. Como cada cubo tiene seis caras, se obtiene el volumen equivalente a tres esferas. Por tanto, la densidad es el volumen de cuatro esferas dividido entre el volumen del cubo. El volumen de cada esfera es ![]() y el volumen del cubo es
y el volumen del cubo es ![]() . Por tatno, al densidad es is
. Por tatno, al densidad es is
![]()
¿Cómo se consigue este empaquetamiento? De la misma manera que cuando apilamos naranjas: primero se coloca una capa de esferas en el plano como en la Figura 2 (b) y encima se coloca una segunda capa con un desplazamiento en una dirección determinada, por ejemplo superior derecha. La tercera capa se coloca encima de la segunda con un desplazamiento en la misma dirección, etc. Esto nos lleva a plantearnos la siguiente pregunta: ¿podemos cambiar la dirección del desplazamiento entre capas sin cambiar la densidad del empaquetado? La respuesta es que sí se puede, pero la correspondiente red de centros no será cúbica centrada en las caras. Esto significa que el empaquetado que da la densidad máxima no es único.
No es obvio que el empaquetado usual de naranjas se corresponda con la red cúbica centrada en las caras. De hecho, si se observa la Figura 7 (b), se puede ver que debería haber líneas ortogonales de centros de esferas alineados. Es un buen ejercicio de visualización imaginar que todas esas líneas existen en el empaquetamiento usual de naranjas pero que ninguna de ellas está contenida en un plano horizontal. De hecho, el plano de la Figura 2 (b) es un plano inclinado a través de los centros de las tres caras adyacentes a un vértice en el cubo de la Figura 7 (a). En la Figura 8 se representa el empaquetado en cuatro capas como en la Figura 2 (b), una encima de otra. Las dos líneas que pasan a través de los centros de las esferas son ortogonales.
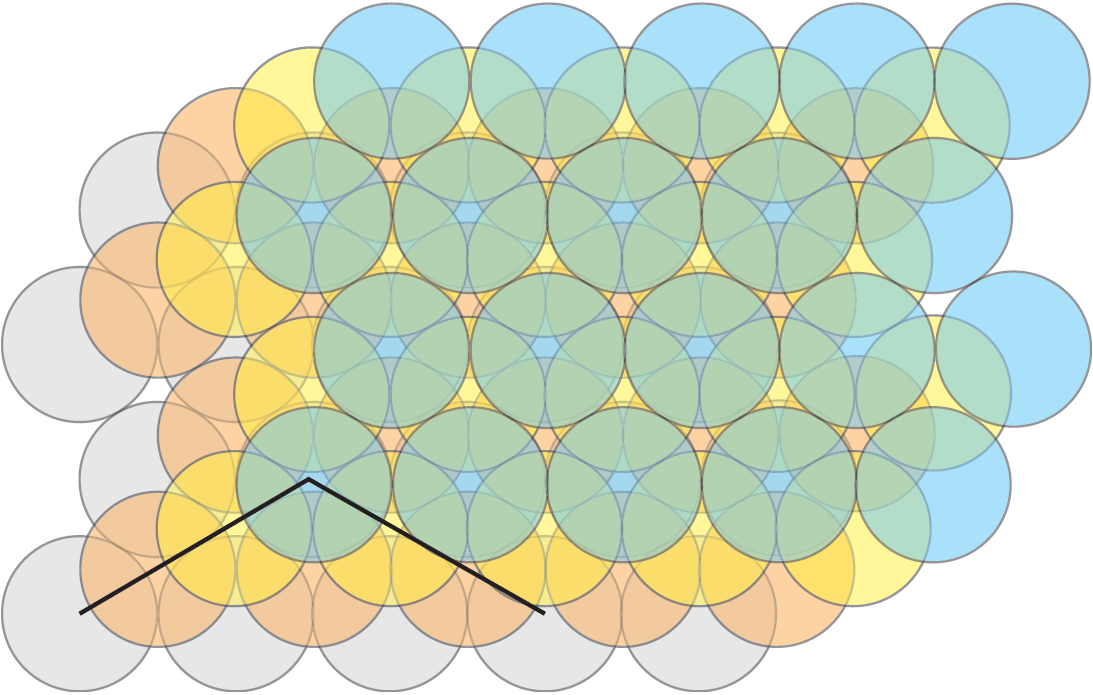
Figura 8: Cuatro capas de esferas del mismo tipo que en la Figura 2 (b), una sobre otra y con dos líneas de centros ortogonales.
4. Expandiendo horizontes.
4.1. Aplicaciones en cristalografía.
La cuestión del empaquetamiento de esferas le fue propuesta por Thomas Harriot a Johannes Kepler a finales del siglo XVI. Ya en ese tiempo, Harriot creía en la existencia de los átomos y estaba interesado en cómo se disponían unos alrededor de otros. Cuando una disposición de átomos en un determinado material es regular, los químicos dicen que dicho material es un cristal. Los materiales pesados, como los metales, habitualmente tienen los átomos colocados en los puntos de una red cúbica centrada en las caras. Existen también otras disposiciones regulares menos densas. Una de los empaquetamientos menos densos es el empaquetamiento cúbico simple, en el cual los átomos se localizan en los vértices de los cubos. Solo existe un elemento químico con esta configuración de átomos: el polonio radiactivo (mas detalles en [4]).
4.2. Empaquetamiento aleatorio.
Si se empaquetan naranjas en grandes cajas cuidadosamente usando el modelo de red cúbica centrada en las caras previamente descrito, se obtiene la densidad ![]() Pero si se tiene prisa y simplemente se dejan caer rápidamente las naranjas en la caja, ¿qué densidad se obtiene? Esto es lo que se conoce como empaquetamiento aleatorio. Por supuesto, la densidad no es siempre la misma. De hecho, si se agita la caja, probablemente la densidad aumente. ¿Hasta cuándo? Los experimentos muestran que la densidad varía desde alrededor del
Pero si se tiene prisa y simplemente se dejan caer rápidamente las naranjas en la caja, ¿qué densidad se obtiene? Esto es lo que se conoce como empaquetamiento aleatorio. Por supuesto, la densidad no es siempre la misma. De hecho, si se agita la caja, probablemente la densidad aumente. ¿Hasta cuándo? Los experimentos muestran que la densidad varía desde alrededor del ![]() (empaquetamiento aleatorio holgado) hasta un máximo de
(empaquetamiento aleatorio holgado) hasta un máximo de ![]() (empaquetamiento aleatorio compacto). El origen de este límite superior fue el asunto de una carta en Nature en 2008 remitida por Song, Wang y Maske [3].
(empaquetamiento aleatorio compacto). El origen de este límite superior fue el asunto de una carta en Nature en 2008 remitida por Song, Wang y Maske [3].
4.3. Empaquetando otros objetos.
Es posible obtener una densidad mayor que ![]() si se cambia la forma de los objetos a empaquetar de esferas a, por ejemplo, elipsoides. El trabajo [1] muestra que la densidad de empaquetamientos aleatorios compactos de esferoides con relación de aspecto como los caramelos M & M pasa de
si se cambia la forma de los objetos a empaquetar de esferas a, por ejemplo, elipsoides. El trabajo [1] muestra que la densidad de empaquetamientos aleatorios compactos de esferoides con relación de aspecto como los caramelos M & M pasa de ![]() a
a ![]() y que la densidad para elipsoides con otras relaciones de aspecto puede incluso acercarse a
y que la densidad para elipsoides con otras relaciones de aspecto puede incluso acercarse a ![]() . La densidad de empaquetados aleatorios es fundamental para la industria cuando se empaquetan objetos iguales (por ejemplo, caramelos o fármacos en pastillas) de manera automática. En particular, la densidad puede variar durante el transporte.
. La densidad de empaquetados aleatorios es fundamental para la industria cuando se empaquetan objetos iguales (por ejemplo, caramelos o fármacos en pastillas) de manera automática. En particular, la densidad puede variar durante el transporte.
4.4. Un comentario acerca de dimensiones más altas.
En dimensiones más altas, los empaquetamientos regulares de hiperesferas más densos se conocen hasta dimensión 8 y no se conoce apenas nada acerca de empaquetamientos no regulares.
Una aplicación de empaquetamientos de esferas en dimensiones más altas se encuentra en la generación de códigos de corrección de errores. El principio básico de un código de detección de errores es codificar las letras o las palabras mediante secuencias de símbolos, llamadas palabras código, que difieren una de otra en al menos ![]() símbolos. Así, si ocurren menos de
símbolos. Así, si ocurren menos de ![]() errores en la transmisión de una palabra código existe al menos una palabra código a distancia menor que
errores en la transmisión de una palabra código existe al menos una palabra código a distancia menor que ![]() de la palabra recibida y la corrección es posible. En los códigos de corrección de errores que usan empaquetamiento de esferas se tranforman las letras del código en tuplas de coordenadas de centros de esferas no superpuestas. Si las esferas tienen radio
de la palabra recibida y la corrección es posible. En los códigos de corrección de errores que usan empaquetamiento de esferas se tranforman las letras del código en tuplas de coordenadas de centros de esferas no superpuestas. Si las esferas tienen radio ![]() entonces es posible corregir menos de
entonces es posible corregir menos de ![]() errores.
errores.
4.5. Las siguientes preguntas…
Deben ser planteadas por el lector. COmo se ha podido ver, hay muchas cuestiones simples con importantes aplicaciones y cuyas sofisticadas respuestas se han publicado en algunas de las revistas científicas de mayor importancia, como Nature, Science o Annals of Mathematics.
5. Validez de las demostraciones asistidas por ordenador.
La demsotración de que el empaquetamiento más denso de discos en el plano en el caso de dimensión dos tiene densidad ![]() demuestra que es posible dar demostraciones rigurosas de resultados en los que hay un número infinito de casos por analizar. Es una demostración que cualquiera puede comprobar. Pero, ¿quién puede probar que
demuestra que es posible dar demostraciones rigurosas de resultados en los que hay un número infinito de casos por analizar. Es una demostración que cualquiera puede comprobar. Pero, ¿quién puede probar que ![]() ? Es una demostración enorme con
? Es una demostración enorme con ![]() casos que analizar y cada caso es tan complejo que necesita hacerse con ayuda de un ordenador, con un total de 3 gigabytes de código. Por supuesto, el código es público, pero les llevó a los autores varios años escribirlo. ¿Quién tiene, por tanto, el tiempo y la habilidad suficientes para revisar, el programa se debería poder ejecutar en diferentes ordenadores con diferentes procesadores y compiladores, las rubrutinas solo podían usar paquetes de software antiguos que hubieran sido probados durante años, etc.
casos que analizar y cada caso es tan complejo que necesita hacerse con ayuda de un ordenador, con un total de 3 gigabytes de código. Por supuesto, el código es público, pero les llevó a los autores varios años escribirlo. ¿Quién tiene, por tanto, el tiempo y la habilidad suficientes para revisar, el programa se debería poder ejecutar en diferentes ordenadores con diferentes procesadores y compiladores, las rubrutinas solo podían usar paquetes de software antiguos que hubieran sido probados durante años, etc.
A pesar de todo ello, estas demostraciones siguen siendo controvertidas y suponen a la comunidad científica un largo proceso de decisión previo a su aceptación. En el caso de la demostración de la conjetura de Kepler, la demostración (reducida) apareció en 2005 en la revista Annals of Mathematics, una de las mejores revistas de matemáticas. Pero la comunidad matemática sigue buscando una demostración más “matemática”. Matemáticos y teóricos de la computación trabajan en paralelo en busca de demostraciones formales, es decir, demostraciones en las cuales cada paso lógic puede ser comprobado por un ordenador. Por ejemplo, la propuesta del proyecto Flyspeck consiste en producir una demostración formal de la conjetura de Kepler:
http://code.google.com/p/flyspeck/wiki/FlyspeckFactSheet
El primer teorema célebre cuya demostración fue asistida por ordenador fue el teorema de los cuatro colores que afirma que cuatro colores son suficientes para colorear cualquier mapa de manera que dos regiones adyacentes no tengan el mismo color. Fue demostrado en 1976 por Kenneth Appel y Wolfgang Haken. En ese tiempo, Annals of Mathematics no habría aceptado publicar una demostración asistida por ordenador. Los tiempos han cambiado y los ordenadores han revolucionado la práctica de las matemáticas.
Referencias.
[1] A. Donev, I. Cisse, D. Sachs, E. Variano, F. H. Stillinger, R. Connelly, S. Tarquato and P.M. Chikin, Improving the density of jammed disordered packings using ellipsoids, Science, 303 (2004), 990–993.
[2] T. Hales, Cannonballs and honeycombs, Notices of the American Mathematical Society, 47 (2000), 440–449.
[3] C. Song, P. Wang and H.A. Maske, A phase diagram for jammed matter, Nature, 453 (2008), 629–-632.
[4] G.C. Szpiro, Kepler’s conjecture, John Wiley & Sons, Inc., 2003.
Este mensaje está disponible en: Inglés, Francés, Alemán, Italiano, Árabe, Khmer

 Español
Español 简体中文
简体中文  English
English  Français
Français  Deutsch
Deutsch  Italiano
Italiano  العربية
العربية  Khmer
Khmer  Português
Português