Übersetzt von Kira Katzenberger und Bettina Rösken-Winter (Ruhr-Universität Bochum)
Bilder, die man auf Internetseiten sehen kann, und Fotos, die mit dem Handy gemacht wurden, sind Beispiele für digitale Bilder. Es ist möglich, diese Art von Bildern durch Matrizen darzustellen. Zum Beispiel kann das kleine Bild von Felix der Katze (Abb. 1) dargestellt werden durch eine ![]() -Matrix, deren Einträge aus den Zahlen
-Matrix, deren Einträge aus den Zahlen ![]() und
und ![]() bestehen. Diese Nummern geben die Farbe jedes Pixels an (ein Pixel ist das kleinste Element eines digitalen Bildes, das nur eine Farbe gleichzeitig annehmen kann): Die Zahl
bestehen. Diese Nummern geben die Farbe jedes Pixels an (ein Pixel ist das kleinste Element eines digitalen Bildes, das nur eine Farbe gleichzeitig annehmen kann): Die Zahl ![]() kennzeichnet die Farbe Schwarz, die Zahl
kennzeichnet die Farbe Schwarz, die Zahl ![]() kennzeichnet die Farbe Weiß. Digitale Bilder, die nur zwei Farben verwenden, werden binäre Bilder oder boolesche Bilder genannt.
kennzeichnet die Farbe Weiß. Digitale Bilder, die nur zwei Farben verwenden, werden binäre Bilder oder boolesche Bilder genannt.
Graustufenbilder können auch durch Matrizen dargestellt werden. Jeder Eintrag der Matrix legt die Intensität des entsprechenden Pixels fest. Der Einfachheit halber nutzen die meisten aktuellen digitalen Dateien ganze Zahlen zwischen ![]() (um Schwarz zu kennzeichnen, die Farbe der geringsten Intensität) und
(um Schwarz zu kennzeichnen, die Farbe der geringsten Intensität) und ![]() (um Weiß zu kennzeichnen, die Farbe der höchsten Intensität), sodass es eine Gesamtmenge von insgesamt
(um Weiß zu kennzeichnen, die Farbe der höchsten Intensität), sodass es eine Gesamtmenge von insgesamt ![]() verschiedenen Graustufen gibt. (Diese Anzahl verschiedener Graustufen genügt, um mit Bildern auf WEB-Seiten zu arbeiten. Allerdings gibt es bestimme spezielle Anwendungen, die mehr Graustufen benötigen, um ein Bild mit mehr Details wiederzugeben und um Rundungsfehler in numerischen Berechnungen zu vermeiden, wie im Fall medizinischer Bilder.)
verschiedenen Graustufen gibt. (Diese Anzahl verschiedener Graustufen genügt, um mit Bildern auf WEB-Seiten zu arbeiten. Allerdings gibt es bestimme spezielle Anwendungen, die mehr Graustufen benötigen, um ein Bild mit mehr Details wiederzugeben und um Rundungsfehler in numerischen Berechnungen zu vermeiden, wie im Fall medizinischer Bilder.)
Farbbilder wiederum können durch drei Matrizen dargestellt werden. Jede Matrix gibt die Menge an Rot, Grün und Blau an, die das Bild enthält. Dieses Farbsystem ist bekannt als RGB. (Es gibt viele andere Farbsysteme, die abhängig von der Anwendung genutzt werden: CMYK (zum Drucken), Y’IQ (für die analoge Übertragung von TV in NTSC), etc.). Die Elemente dieser Matrizen sind ganze Zahlen zwischen ![]() und
und ![]() , und sie legen die Intensität der Pixel bezüglich der Farbe, welche die jeweilige Matrix liefert, fest. Demnach ist es im RGB-System möglich 2563= 224= 16777216 verschiedene Farben darzustellen.
, und sie legen die Intensität der Pixel bezüglich der Farbe, welche die jeweilige Matrix liefert, fest. Demnach ist es im RGB-System möglich 2563= 224= 16777216 verschiedene Farben darzustellen.
Digitale Bildverarbeitung und Operationen mit Matrizen
Wenn digitale Bilder mit Hilfe von Matrizen dargestellt werden, können wir fragen, wie Operationen und Veränderungen der Matrizeneinträge das zugehörige Bild verändern. Wenn wir zum Beispiel das binäre Bild ![]() (siehe Abb. 4) als Matrix
(siehe Abb. 4) als Matrix ![]() betrachten, dann gehört Bild
betrachten, dann gehört Bild ![]() zu der transponierten Matrix von
zu der transponierten Matrix von ![]() , sprich
, sprich ![]() . Das Bild
. Das Bild ![]() gehört dann zum Beispiel zu der Matrix
gehört dann zum Beispiel zu der Matrix ![]() . Versuchen Sie herauszufinden, in welcher Beziehung die anderen Bilder zur Matrix
. Versuchen Sie herauszufinden, in welcher Beziehung die anderen Bilder zur Matrix ![]() stehen!
stehen!
Ein anderes Beispiel: Wenn wir die arithmetischen Mittel der Matrizen der Rot-, Grün- und Blaukomponenten (R,G und B) eines Farbbildes ![]() nehmen, bekommen wir eine Graustufenversion des Bildes (Werte nicht-ganzer Zahlen werden auf die nächste ganze Zahl gerundet):
nehmen, bekommen wir eine Graustufenversion des Bildes (Werte nicht-ganzer Zahlen werden auf die nächste ganze Zahl gerundet):
Ein weiteres Beispiel: Wenn man die Operationen Multiplikation mit einem Skalar und Addieren von Matrizen ausführt, ist es möglich, einen Bildübergangseffekt zu erzeugen, wie er üblicherweise in PowerPoint![]() -Präsentationen und bei Diavorführungen genutzt wird. Genauer gesagt betrachtet man zwei Graustufenbilder derselben Größe, dargestellt durch die Matrizen
-Präsentationen und bei Diavorführungen genutzt wird. Genauer gesagt betrachtet man zwei Graustufenbilder derselben Größe, dargestellt durch die Matrizen ![]() und
und ![]() . Für jeden Skalar (eine reelle Zahl)
. Für jeden Skalar (eine reelle Zahl) ![]() aus dem Intervall
aus dem Intervall ![]() definieren wir die Matrix
definieren wir die Matrix
![]()
Dann ist ![]() ,
, ![]() und für jedes
und für jedes ![]() zwischen
zwischen ![]() und
und ![]() liegen die Einträge der Matrix
liegen die Einträge der Matrix ![]() zwischen denen der Matrizen
zwischen denen der Matrizen ![]() und
und ![]() . Deshalb variiert die Matrix
. Deshalb variiert die Matrix ![]() von
von ![]() bis
bis ![]() , wenn
, wenn ![]() Werte von
Werte von ![]() bis
bis ![]() durchläuft. Im Fall von Farbbildern muss die obige Transformation die Matrizen
durchläuft. Im Fall von Farbbildern muss die obige Transformation die Matrizen ![]() ,
, ![]() und
und ![]() betreffen, aus denen sich jedes Bild zusammensetzt.
betreffen, aus denen sich jedes Bild zusammensetzt.
Auch Matrizenmultiplikationen haben Anwendungen in der digitalen Bildverarbeitung. Obwohl unser nächstes Beispiel aufwändiger ist (mit einem Gegenstand, der fortgeschrittener mathematischer Techniken bedarf, die normalerweise nur in Linearer Algebra an Universitäten gelernt werden), glauben wir trotzdem, dass diese Anwendung für den Leser von Interesse ist. Dieses Beispiel bietet die Möglichkeit, eine erstaunliche Anwendung zu genießen, welche sich aus der Möglichkeit ergibt, eine Matrix zu zerlegen und als Produkt von Matrizen mit speziellen Strukturen darzustellen. Die weggelassenen Details können der Literatur [Lay, 2011] und [Poole, 2005] entnommen werden. Wir betrachten dafür eine Singulärwertzerlegung (SVD für singular value decomposition), die daraus besteht, eine Matrix als Produkt von drei Matrizen darzustellen:
![]()
wobei U und V orthogonale Matrizen sind (das heißt ![]() und
und ![]() sind
sind ![]() – bzw.
– bzw. ![]() – Einheitsmatrizen) und S ist eine Matrix mit Einträgen
– Einheitsmatrizen) und S ist eine Matrix mit Einträgen ![]() , die gleich Null sind für
, die gleich Null sind für ![]() und
und ![]() , mit
, mit ![]() . Es folgt ein Beispiel für eine Singulärwertzerlegung:
. Es folgt ein Beispiel für eine Singulärwertzerlegung:
![]()
![Rendered by QuickLaTeX.com \[= \left[ \begin{array}{rr} \displaystyle -\frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{2}}{2} \vspace*{0.5ex} \\ \displaystyle \frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{2}}{2} \end{array} \right] \left[ \begin{array}{rrr} \sqrt{3} & 0 & 0 \\ 0 & 1 & 0 \end{array} \right] \left[ \begin{array}{rrr} \displaystyle \frac{\sqrt{6}}{6} & \displaystyle -\frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{3}}{3} \vspace*{0.5ex} \\ \displaystyle -\frac{\sqrt{6}}{3} & 0 & \displaystyle \frac{\sqrt{3}}{3} \vspace*{0.5ex} \\ \displaystyle \frac{\sqrt{6}}{6} & \displaystyle \frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{3}}{3} \end{array} \right]^{T}. $ } }\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-5b078445b1a0c61f0876bb5f96595de0_l3.png)
Es kann gezeigt werden, dass jede Matrix eine Singulärwertzerlegung besitzt ([Lay, 2011], [Poole, 2005]). Außerdem existieren Algorithmen, die es uns ermöglichen, solche Zerlegungen mit Hilfe eines Computers zu berechnen. Der entscheidende Punkt unseres Beispiels ist, zu betrachten, dass, wenn ![]() die Spalten der Matrix
die Spalten der Matrix ![]() und
und ![]() die Spalten der Matrix
die Spalten der Matrix ![]() sind, dann ist
sind, dann ist
![]()
Warum geht man so vor? Angenommen ![]() , ein Graustufenbild der Größe
, ein Graustufenbild der Größe ![]() , muss von einem Satelliten zu einem Labor auf der Erde übertragen werden. Im Prinzip müsste der Satellit eine Millionen Zahlen (eine für jedes Pixel) senden. Da typischerweise nur die ersten Einträge
, muss von einem Satelliten zu einem Labor auf der Erde übertragen werden. Im Prinzip müsste der Satellit eine Millionen Zahlen (eine für jedes Pixel) senden. Da typischerweise nur die ersten Einträge ![]() der Matrix
der Matrix ![]() der Singulärwertzerlegung von
der Singulärwertzerlegung von ![]() bedeutend sind (die anderen sind „klein“), genügt es demnach, dass der Satellit, sagen wir, die ersten
bedeutend sind (die anderen sind „klein“), genügt es demnach, dass der Satellit, sagen wir, die ersten ![]() Spalten von
Spalten von ![]() und
und ![]() sendet sowie die
sendet sowie die ![]() ersten Einträge
ersten Einträge ![]() (insgesamt müssen also nur
(insgesamt müssen also nur ![]() Zahlen gesendet werden). Aufgrund dieser Daten berechnet das Labor auf der Erde die Matrix
Zahlen gesendet werden). Aufgrund dieser Daten berechnet das Labor auf der Erde die Matrix ![]() , die eine Approximation des Originalbildes ermöglicht.
, die eine Approximation des Originalbildes ermöglicht.
Betrachten wir ein Beispiel: Das Bild des Mathematikers Christian Felix Klein(1849-1925) (siehe Abb. 7), hat ![]() Pixel.
Pixel.
Aus der Singulärwertzerlegung der zugehörigen Matrix des Bildes können wir die Matrizen ![]() für
für ![]() und
und ![]() berechnen. Diese Matrizen erzeugen Approximationen des Originalbildes, wie in den folgenden Bildern zu sehen ist. Beachten Sie, dass das Originalbild zu dem Wert
berechnen. Diese Matrizen erzeugen Approximationen des Originalbildes, wie in den folgenden Bildern zu sehen ist. Beachten Sie, dass das Originalbild zu dem Wert ![]() gehört. Das Ergebnis ist ziemlich eindrucksvoll, nicht wahr?
gehört. Das Ergebnis ist ziemlich eindrucksvoll, nicht wahr?
Weitere Anwendungen
Digitale Bildverarbeitung hat viele Anwendungen, zum Beispiel bei der Fernerkundung, der Datenübermittlung, der Medizin, Robotern, Computer, der Filmindustrie, etc. In der Fernerkundung zum Beispiel, sind Bilder, die von Satelliten aufgenommen wurden, hilfreich, um natürliche Ressourcen etwa für geographische Kartierung, zur Analyse der Städteausdehnung und viele weitere ökologische Anwendungen zu erhalten. Bei der Bildübertragung gibt es zum Beispiel die Kommunikation via Fax, Netzwerke, das Internet oder Videoüberwachung. Zur medizinischen Anwendungen gehören die Entwicklung von Röntgenbildern, Projektionsbildern bei Computertomographien, Radiologie, Magnetresonanztomographien (MRT) und bei Ultraschalluntersuchungen.
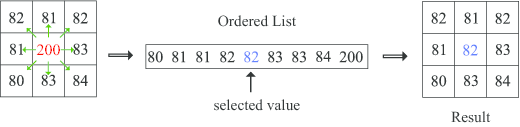
Einige Methoden der Erfassung und Übertragung können Störungen in Bildern verursachen. Der Medianfilter ist eine Bildbearbeitungstechnik, die genutzt wird, um diese Störungen zu entfernen oder deren Effekte zu reduzieren: Für jeden Eintrag der Matrix betrachten wir die benachbarten Einträge und ordnen alle in einer Liste an. Der Medianfilter besteht daraus, dass der mittlere Wert der Liste ausgewählt und der zentrale Eintrag durch diesen Wert ersetzt wird.
Es gibt viele weitere Techniken in der Bildvearbeitung mit anderen Zielen. Die folgenden Bilder zeigen Beispiele für Kontrastregulierung, Kantenerkennung und Schwellenwertregulierung.
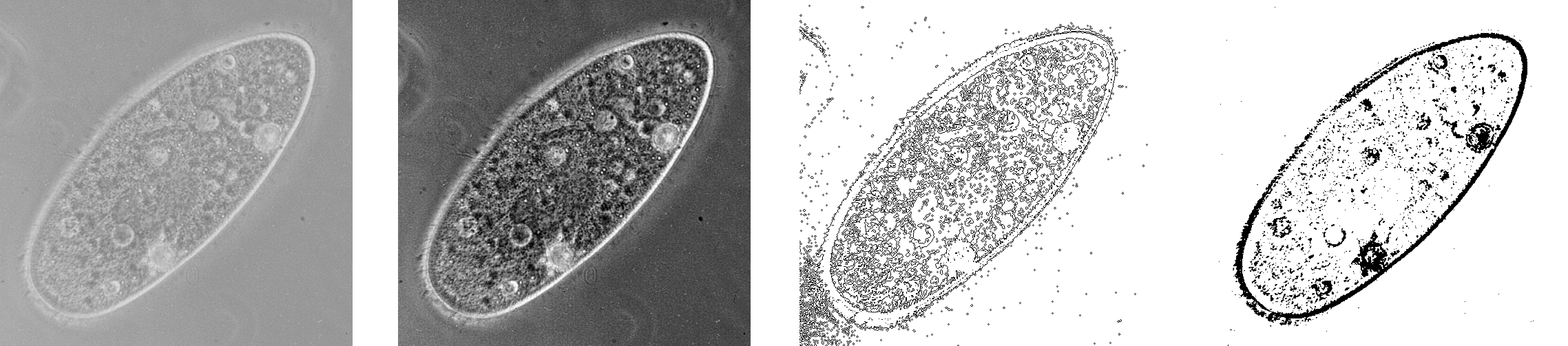
Abb. 11: Originalbild und dasselbe Bild mit Kontrastregulierung, Kantenerkennung und Schwellenwertregulierung.
Abschlussbemerkung
Unser Ziel mit diesem Beitrag ist es, die für Lehrer und Schüler wenig bekannte Anwendung von Matrizen vorzustellen: Die Bearbeitung von digitalen Bildern. Es ist wichtig zu beachten, dass die mathematischen Werkzeuge, die mit diesem Thema in Verbindung stehen, weit über Matrizen hinaus reichen. Das Thema ist umfangreich, reichhaltig und zeitgemäß. Leider erlaubt uns die für diesen Artikel empfohlene Beschränkung auf wenige Seiten nicht, auf weitere Details einzugehen. Als Vertiefung für Leser, die motiviert sind mehr über das Thema herauszufinden, empfehlen wir die Bücher [Gonzales und Woods, 2007] und [Gomes und Velho, 2008].
Quellen
Auf dieser Website gibt es eine Reihe interaktiver Anwendungen, die es erlauben, die Beziehungen zwischen Matrizen und digitalen Bildern, die in diesem Text vorgestellt wurden, zu erkunden. Dort findet sich auch ein DOC-Dokument mit Aufgabenvorschlägen, die im Unterricht eingesetzt werden können.
Dies sind die im Text zitierten Quellen:
Gomes, J.; Velho, L. Image Processing for Computer Graphics and Vision. Springer-Verlag, 2008.
Gonzalez, R. C.; Woods, R. E. Digital Image Processing. Third Edition. Prentice Hall, 2007.
Lay, D. Linear Algebra and Its Applications. Forth Edition. Addison Wesley, 2011.
Poole, D. Linear Algebra: A Modern Introduction. Second Edition. Brooks Vole, 2005.
Das Foto der Mona Lisa in LEGO ist Eigentum von Marco Pece Udronotto, der freundlicherweise genehmigt hat, sein Werk in dieser Arbeit zu verwenden.
Andere Sprachen: Englisch, Französisch, Italienisch, Arabisch, Khmer










 Deutsch
Deutsch 简体中文
简体中文  English
English  Français
Français  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português