 Vignette écrite par Gabriel Rosenberg et Mark Iwen.
Vignette écrite par Gabriel Rosenberg et Mark Iwen.
C’est un fait peu connu que deux médailles d’or ont été attribuées à l’épreuve de patinage artistique des jeux Olympiques d’hiver de 2002. Ces deux médailles ont finalement été le résultat d’un vote litigieux qui débuta avec la défaite du couple favoris du public. Le scandale autour de cette décision a été si grand que le Comité international olympique (COI) a finalement dû accorder une deuxième médaille d’or au couple arrivé second en patinage artistique afin d’apaiser le scandale. Le système de vote pour décider quels patineurs méritent quelles médailles a également été modifié (NB: Avant 2003 les juges notaient individuellement les participants et utilisaient ces résultats pour classer les athlètes. Ces classements (et non les scores) étaient combinés pour attribuer les récompenses).
Imaginez que vous soyez au COI en 2003 et que la tâche de développer un meilleur système de vote pour juger les compétitions de patinage artistique à venir vous a été attribuée. Quel système de vote choisiriez-vous pour classer les patineurs? Comment pourriez-vous vous assurer que que le système de vote est équitable? Évidemment les mathématiques peuvent nous aider à répondre à ces questions!
Les fonctions à la rescousse: Le Pouvoir de l’Abstraction
Une façon de penser pour créer un nouveau système de vote pour évaluer les patineurs (ou un nouveau système de vote pour toute autre utilisation) consiste à considérer tous les systèmes de vote possibles. On peut alors construire un bon système de vote en restreignant lentement tous les systèmes possibles à un plus petit ensemble de possibilités souhaitables. En procédant de cette façon on peut espérer ne passer à coté que de peu de possibilités, et donc garder nos options aussi ouvertes que possibles.
Commençons en modélisant (une classe très générale) de tous les systèmes de vote possibles. Tout système dans cet ensemble va finalement devoir un ensemble de patineuses en se basant sur les données fournies par un ensemble de votants (e. g. les juges olympiques). Supposons que notre ensemble de patineuses soit ![]() , chacune d’elles est notée par chacun des juges de l’ensemble de juges suivant,
, chacune d’elles est notée par chacun des juges de l’ensemble de juges suivant,
![]()
![]()
Chaque juge donne des scores pour les patineuses ce qui produit un différent classement des patineuses pour chaque juge. Par exemple, les scores des juges pour une compétition donnée pourrait se terminer avec les classements individuels suivants (voir le Tableau 1).
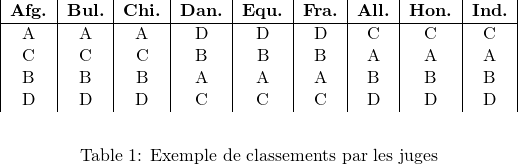
Tout système de vote doit prendre cet ensemble de neuf classement individuels par chaque juge et donner en retour un unique classement donnant le premier (or), second (argent), troisième (bronze), quatrième, cinquième, etc. de l’ensemble des patineurs, ![]() . Mathématiquement, on peut voir que nos systèmes de vote sont précisément l’ensemble des fonctions qui acceptent
. Mathématiquement, on peut voir que nos systèmes de vote sont précisément l’ensemble des fonctions qui acceptent ![]() classements de
classements de ![]() comme entrée, et produisent un classement final de
comme entrée, et produisent un classement final de ![]() en sortie. Ici
en sortie. Ici ![]() représente le nombre de juges dans
représente le nombre de juges dans ![]() .
.
Les qualités qu’un bon système de vote doit avoir
Bien sûr, on peut voir immédiatement que cet ensemble de fonctions est trop général pour être équitable. Par exemple, la fonction qui associe toujours au second patineur (i.e. Berezhnaya dans ce cas) la médaille d’or peu importe comment les juges votent, fait partie de l’ensemble des systèmes de vote. Nous avons clairement besoin de restreindre davantage les fonctions de vote afin de se débarrasser de systèmes de votes si peu équitables.
Respecter les opinions unanimes:La condition de Pareto
La condition de Pareto est une qualité que chaque système de vote devrait avoir. Énoncée simplement, la condition de Pareto exige que si un patineur est classé devant un autre par tous les juges, alors un bon système de vote doit finalement classer ce patineur mieux que les autres (e.g. si Cohen est classée devant Berezhnaya par tous les juges, alors elle doit être classée devant Berezhnaya sur le podium). Cette condition garantit qu’un système de vote respecte les opinions unanimes.
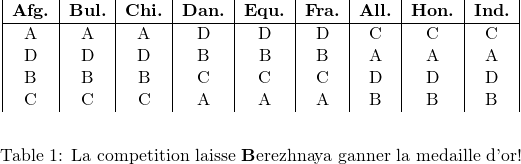
Bien qu’il soit difficile de concevoir un système de vote naturel qui conduise à un résultat qui ne satisfait aucun votant, ceci peut en fait arriver lorsque le système de vote est de nature hiérarchique. Considérons par exemple que chacun de nos quatre participants patine dans l’ordre suivant: Asada, Dijkstra, Cohen, et Berezhnaya. Asada et Dijkstra sont les deux premiers à patiner, et après leurs performances les juges préfèrent Asada avec 6 votes contre 3. Ensuite, Cohen entre en piste, et les juges vote encore à 6 contre 3 que Cohen est meilleure patineuse que Asada. Enfin, Berezhnhaya patine, et les juges pensent que Berezhnaya est meilleure que Cohen à 6 votes contre 3. Un système de vote basé sur ces comparaisons de deux patineurs peut alors conduire au classement Berezhnaya (gold), Cohen (silver), Asada (bronze), et Dijkstra. Lorsque les juges donnent leurs classements individuels (comme dans le tableau 2 où chaque colonne représente le classement d’un juge de la plus haute place en haut à la plus basse en bas) ils sont surpris de découvrir que chacun d’eux a pensé que Dijkstra avait patiné mieux que Berezhnaya. La médaille d’or a été attribuée à une patineuse qui a été unanimement considéré comme pire que le quatrième patineuse de la compétition!
Indépendance d’alternatives inutiles
Imaginez la situation suivante: Supposons que Asada et Berezhnaya aient déjà patiné, mais pas Cohen. Dans cette situation, les juges ont décidé lequel des deux premiers patineurs ils préfèrent, mais ne sont pas encore sûrs du résultat de Cohen puisqu’elle n’a pas encore patiné. Les membres de l’administration des jeux veulent cependant savoir le résultat à ce stade (e.g. avant une coupure de publicité). Ainsi, les juges doivent classer Cohen selon son résultat probable. La fonction de vote est évaluée, et il en résulte que Asada doit terminer devant Berezhnaya sur le podium. La fonction de vote classe également Cohen sur le podium, mais tout le monde sait que le classement n’est qu’une supposition probable susceptible de changer lorsque que Cohen aura patiné.
Plus tard, après la coupure, Cohen patine et certains juges changent leurs avis selon la performance de Cohen. Cependant il ne changent pas le rang de Asada par rapport à celui de Berezhnaya. Lorsque les résultats officiels sont établis par la fonction de vote, il apparaît que Berezhnaya termine au-dessus de Asada sur le podium! Cela paraît injuste. Pourquoi le classement de Cohen détermine-t-il ceux de deux autres patineuses? On dit qu’un système dans lequel un comportement si étrange ne peut pas arriver satisfait l’Idépendance des Alternatives Non-Pertinente (IANP). Grossièrement, un système de vote qui satisfait l’IANP ne changera pas un classement partiel établi précédemment en se basant sur de future résultats.
Les opinions améliorées ne devraient pas blesser: Monotonie
Imaginez maintenant une situation où les résultats ont été annoncés avec Asada à la première place, Berezhnaya à la seconde, et Cohen à la troisième. Le juge Bulgare signale alors que son vote a été mal lu. Son vote a été lu de la façon suivante: Asada, Berezhnaya, Cohen, alors qu’elle a voté Berezhnaya, Asada, Cohen. Les membres de l’administration des jeux recalculent les résultats et déclarent que maintenant Berezhnaya est finalement à la seconde place. Ceci paraît étrange — être mieux classé par un juge peut faire perdre une place à Berezhnaya sur le podium! On dit qu’un système dans lequel une situation si étrange ne peut pas arriver est monotone.
A première vue il paraît étrange de considérer une telle propriété. Quelle sorte de système de vote dégraderait le classement d’une patineuse dont le résultat serait plus élevé? Souvenons-nous qu’un système de vote n’est qu’une fonction et rien ne l’oblige à être logique. C’est à nous qu’il appartient de décider quel système convient.
Il est intéressant de remarquer que cette simple propriété n’est pas respectée par des système de vote très communs. En fait, un système de vote utilisant une série de votes successifs, comme celui utilisé par le COI pour choisir une ville pour accueillir les jeux, n’est pas monotone. La fréquence des situations non monotones est actuellement le sujet de nombreuses recherches et débats.
Egalité: Neutralité et Anonymat
Une autre propriété que l’on peut désirer pour un système de vote, en terme d’équité, est qu’il traite toutes les patineuses de façon juste. C’est-à-dire que les patineuses devraient être classées indépendamment de leur ordre de passage, leur nom, leur nationalité, etc. Nous dirons qu’un système de vote avec ces caractéristiques est neutre. De même, on peut vouloir qu’un système accorde autant d’importance à chaque juge. En d’autres termes, la valeur accordée au vote de chaque juge pour la décision du résultat final ne devrait pas non plus dépendre de l’ordre des juges, de leurs noms, nationalités, etc. Un système de vote qui satisfait cette propriété est dit anonyme.
On peut se rendre compte que certains systèmes de vote courants (et démocratiques!) n’ont pas ces propriétés. Par exemple, chaque pays qui élit ses dirigeants en recoupant les votes de plusieurs zone géographiques ne remplit pas le critère d’anonymat. Aux Etats-Unis par exemple, les votants des états supportant majoritairement un parti politique peuvent voir leurs votes compter “davantage” en votant temporairement dans un autre état où le résultat des élections est plus incertain. C’est exactement pourquoi les votants des “swing states” ont plus de pouvoir pour influencer quel candidat obtiendra les votes de leur état.
Une mauvaise nouvelle: Le théorème d’impossibilité d’Arrow
Nous disposons maintenant de plusieurs critères raisonnables que le système de vote Olympique pourrait satisfaire. Dans cette section, nous allons essayer de déterminer un ensemble de bons systèmes de vote possédant toutes les propriétés dont nous avons parlé précédemment. Encore une fois nous allons nous pencher sur le cas de neuf juges classant 3 patineuses.
Supposons que nous décidons de tester un nouveau système de vote qui semble satisfaire les critères de IANP, monotonie, et neutralité. Pour tester ce nouveau système, considérons le cas où il y a trois ensembles de juges. Disons que les trois juges des pays Asiatiques préfèrent les trois patineuses suivantes, dans cet ordre: Asada, Berezhnaya, Cohen. Par ailleurs, supposons que les deux juges Américains préfèrent les patineuses suivants dans cet ordre: Cohen, Asada, Berezhnaya. Finalement, disons que les quatre juges Européens décident de classer les patineuses dans l’ordre suivant: Berezhnaya, Cohen, Asada. Notre système de vote doit nous renvoyer un ordre pour le podium, mais quel peut être cet ordre?
En Poursuivant notre exemple, supposons que notre système de vote nous donne le podium suivant: Berezhnaya devant Asada. Puisque notre système satisfait la condition IANP, cela implique que si les juges Européens classaient Berezhnaya devant Asada, et que les six autres juges classaient Asada devant Berezhnaya, on devrait avoir Berezhnaya devant Asada sur le podium (i.e. la position de Cohen ne changera rien à la position de Berezhnaya par rapport à Asada!). Puisque notre système de vote est monotone, ce résultat devrait encore être valide si certains des cinq autres classaient aussi Berezhnaya devant Asada (i.e. ceci devrait seulement améliorer le classement de Berezhnaya!). Ainsi les quatre juges Européens ont un pouvoir de décision absolue sur le classement dans le sens où à CHAQUE fois qu’ils classent Berezhnaya devant Asada, ils sont certains que Berezhnaya finira devant Asada. Puisque notre système est neutre, il n’y a rien de spécial pour Berezhnaya et Asada dans cet exemple. A chaque fois que les juges Européens classent une patineuse devant une autre, les patineuses doivent arriver dans cet ordre sur le podium. Donc si les juges Européens votent en bloc (i.e. en votant tous de la même façon) le résultat sur le podium sera le leur, peu importe comment les cinq autres groupes de juges votent. On dit que les juges Européens ont un pouvoir dictatorial.
Comme résultat de cette discussion, on peut se demander si le profil présenté ne devrait pas aboutir à Berezhnaya arrivant devant of Asada sur le podium. Supposons plutôt que Asada doive finir devant Berezhnaya. On se demande alors à quelle place Cohen serait placé, relativement à Berezhnaya. Si l’ordre sur le podium donne Cohen devant Berezhnaya, alors nous sommes dans une situation où les juges Américains sont les seuls à placer Cohen devant Berezhnaya (résultant en un ordre sur le podium reflétant leurs préférences). Avec le même raisonnement que précédemment, ceci implique que les juges Américains ont un pouvoir dictatorial! Si on ne veut pas qu’une minorité ait de pouvoir dictatorial, nous devons alors placer Asada devant Berezhnaya devant Cohen sur le podium. Mais alors Asada termine devant Cohen. Sachant que seuls les juges Asiatiques donnaient ce résultat dans leur classement, cela implique que les juges Asiatiques ont alors un pouvoir dictatorial. On ne peut échapper à une dictature!
Puisque notre système de vote doit conduire à un classement sur le podium pour ce profil, un de nos trois groupes de juges doit avoir un pouvoir dictatorial. C’est-à-dire que dans chaque situation dans laquelle ce groupe vote en bloc le même classement, alors le résultat sur le podium respectera cet ordre. Une fois que l’on a un groupe dictatorial on pourrait aussi le diviser en sous groupes et en utilisant un raisonnement similaire on pourrait montrer qu’un de ces sous groupe est dictatorial. En continuant ces divisions on obtiendra finalement un groupe dictatorial constitué d’un seul juge – un dictateur. Kenneth Arrow a prouvé ces résultats en 1950 même dans le cas de conditions plus faibles où le système ne vérifie que les conditions IANP et Pareto.
Théorie de vote
Arrow a été un des premiers à étudier le vote d’un point de vue mathématiques, c’est-à-dire comme des fonctions ayant ou non certaines propriétés. Son travail, cependant, a ouvert la porte à un nouveau domaine de recherche dans lequel les mathématiciens, économistes et chercheurs en politique se croisent et partagent des idées sur ce qui est possible et envisageable. Par exemple Allan Gibbard en 1973 et Mark Satterthwaite en 1975 se sont penchés à la propriété d’un système de vote d’être manipulable. En d’autres termes, y a-t-il un système où quelqu’un pourrait obtenir un résultat à son avantage en modifiant son vote. Leur travail a abouti à la conclusion que les seuls systèmes de vote à ne pas être manipulables ont un dictateur, ou alors ont au moins un candidat qui ne peut pas gagner. D’autres chercheurs se sont questionnés sur la possibilité de telles manipulations, et de la probabilité qu’une telle chose arrive.
Morale
Nous voyons alors que le raisonnement mathématiques, par des définitions précises et des preuves logiques, peut être appliqué à des situations se situant au-delà des mathématiques et des sciences naturelles. Un tel raisonnement peut être nécessaire pour convaincre quelqu’un d’un résultat qui à première vue semble contre-intuitif. Dans le contexte de notre exemple olympique, on peut voir que c’est impossible de satisfaire les quatre bonnes caractéristiques que l’on peut désirer pour notre système de vote, du moins s’il est basé uniquement sur le vote des juges.
Il n’est cependant pas nécessaire de désespérer. Notre analyse ci-dessus montre simplement que nous devons considérer une classe plus large de systèmes de vote pour notre recherche d’un bon système. Des solutions d’exemple implique en réalité d’utiliser les scores numériques donnés par les juges, et non simplement des classements. Une autre possibilité serait d’introduire un petit paramètre aléatoire dans le système de vote. Par exemple, on pourrait parfois diminuer le vote d’un juge choisi de façon aléatoire, établissant ainsi un système de vote qui n’es pas une fonction de la forme que nous avons considérée. Cette solution est en fait un des aspects adoptés dans le nouveau système de vote pour patinage artistique établi en 2004!
Références
For All Practical Purposes par COMAP, 8ème ed., W.H. Freeman & Company, 2008.
G. Szpiro, Numbers Rule: The Vexing Mathematics of Democracy, from Plato to the Present, Princeton University Press, 2010.
P. Tannebaum & R. Arnold, Excursions In Modern Mathematics, 7ème edition, Prentice Hall, 2009.
Ce post est disponible en: Anglais, Allemand, Italien, Arabe, Khmère

 Français
Français 简体中文
简体中文  English
English  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português