 Originating author is Christiane Rousseau.
Originating author is Christiane Rousseau.
What is the densest packing of spheres? Kepler conjectured that it was the one you observe with oranges at the fruit shop, and which is called the face-centered cubic lattice (Figure 1). At the International Congress of Mathematicians in 1900, David Hilbert gave a very famous lecture in which he stated 23 problems that would have deep significance for the advance of mathematical science in the 20-th century. The problem of the densest packing of spheres, also called Kepler’s conjecture, is part of Hilbert’s 18-th problem. Kepler’s conjecture was only proved in 1998 by Thomas Hales, and the details of the proof were published in 2006.
1. How do we deal with such problems?
We consider different configurations of equal spheres (solid balls) in space and, in each case, we calculate the density of the packing, i.e. the fraction of the total volume which is occupied by the spheres. We will call ![]() the maximum density of a sphere packing in dimension
the maximum density of a sphere packing in dimension ![]() . Of course, this density depends of the shape of the region. To avoid this, we consider very large regions, so that the effect of the boundary be negligible. Kepler conjectured in 1611 that the densest configuration is the one you observe with oranges at the fruit market. So, why did it take so long to prove this conjecture? The problem is that there are an infinite number of possible configurations of the spheres. Each time we take a configuration, we can show that its density is less than or equal to the one observed at the fruit market. But the problem is that we can only describe a finite number of configurations. And, even with a single configuration, the computation of its density may be difficult or impossible if the configuration is not periodic.
. Of course, this density depends of the shape of the region. To avoid this, we consider very large regions, so that the effect of the boundary be negligible. Kepler conjectured in 1611 that the densest configuration is the one you observe with oranges at the fruit market. So, why did it take so long to prove this conjecture? The problem is that there are an infinite number of possible configurations of the spheres. Each time we take a configuration, we can show that its density is less than or equal to the one observed at the fruit market. But the problem is that we can only describe a finite number of configurations. And, even with a single configuration, the computation of its density may be difficult or impossible if the configuration is not periodic.
The problem of the densest packing of solid balls exists in all dimensions. It was solved in 1890 for ![]() -dimensional solid balls. Packing of balls in higher dimensions have applications in, for instance, error correcting codes.
-dimensional solid balls. Packing of balls in higher dimensions have applications in, for instance, error correcting codes.
Already, in dimension ![]() we encounter the same two difficulties: we cannot enumerate all configurations and, moreover, some configurations may not be periodic. We will show how we deal with these difficulties, and that the packing of Figure 2(b) is the densest of all configurations. We will then explain the difficulties to generalize the proof to the
we encounter the same two difficulties: we cannot enumerate all configurations and, moreover, some configurations may not be periodic. We will show how we deal with these difficulties, and that the packing of Figure 2(b) is the densest of all configurations. We will then explain the difficulties to generalize the proof to the ![]() -dimensional case, and we end up with a few words on higher dimensions.
-dimensional case, and we end up with a few words on higher dimensions.
2. The two-dimensional case.
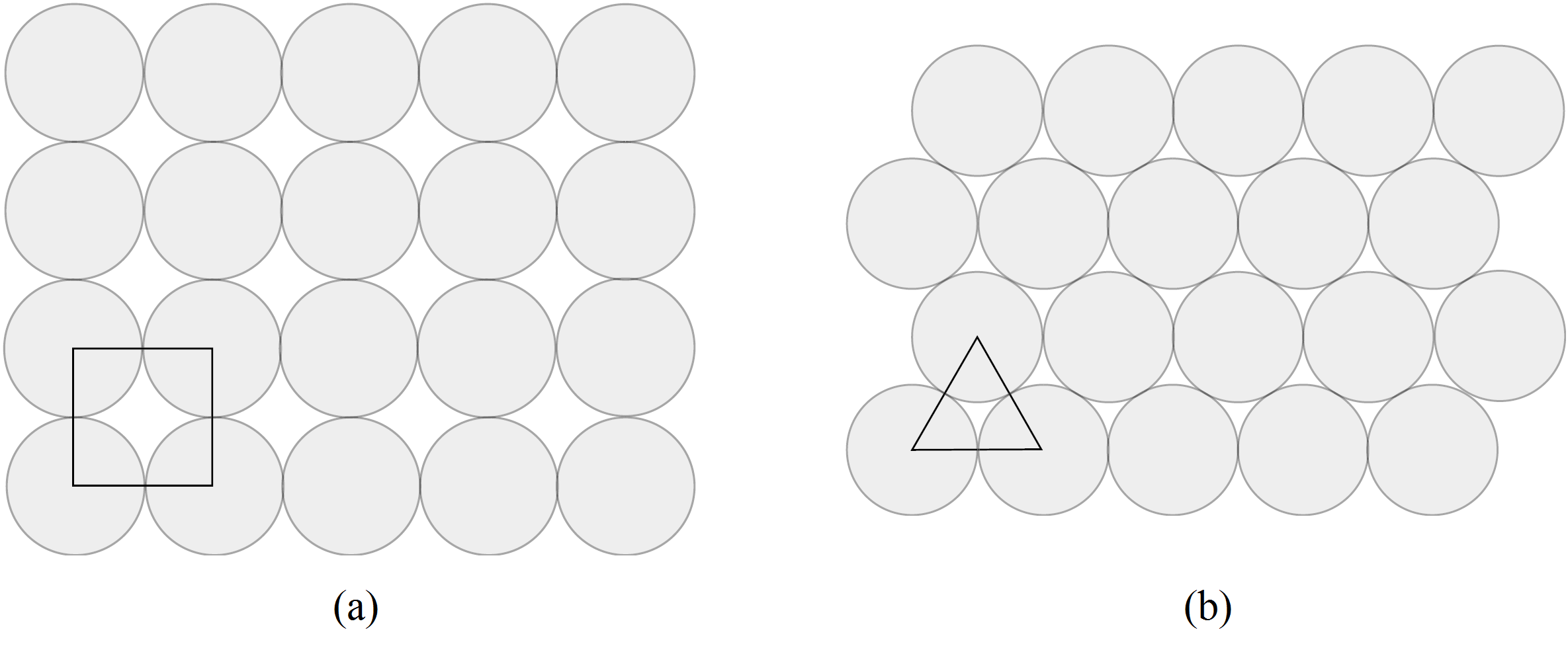
Consider the two packings of disks in Figure 2. It is an easy exercise to compute the proportion of each square covered by portions of disks in case (a) and the proportion of each triangle covered by portions of disks in case (b). If we do so, we see that the second packing is denser. Indeed the packing (a) has density ![]() and the packing (b) has density
and the packing (b) has density
![]()
Each time we consider a periodic packing, we can show that it is less dense than the packing of Figure 2 (b).
But, how do we show that this is also the case for any packing?
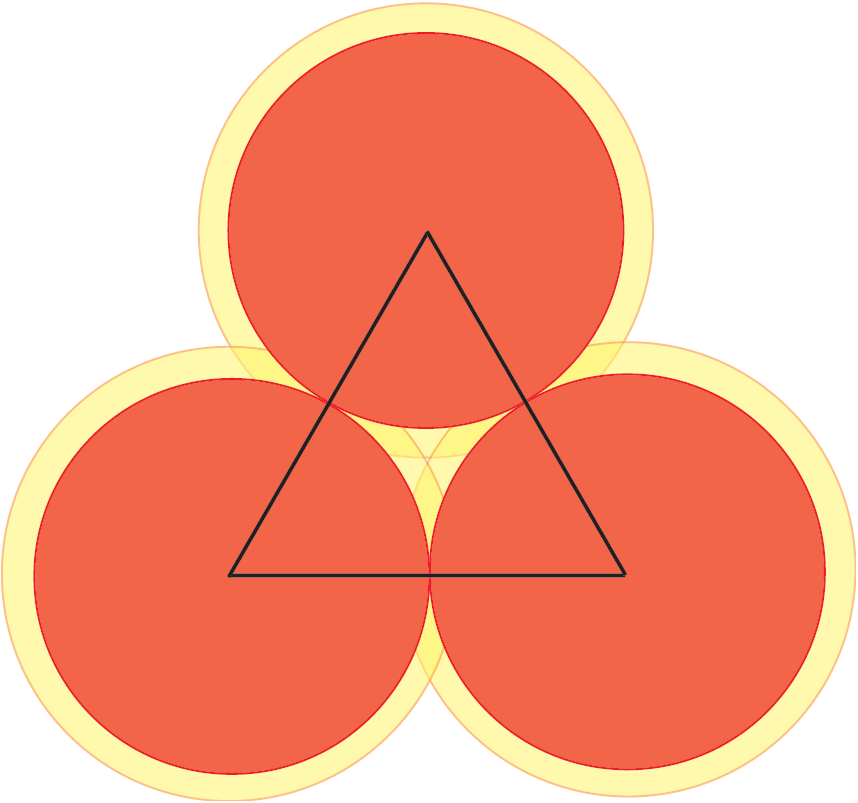
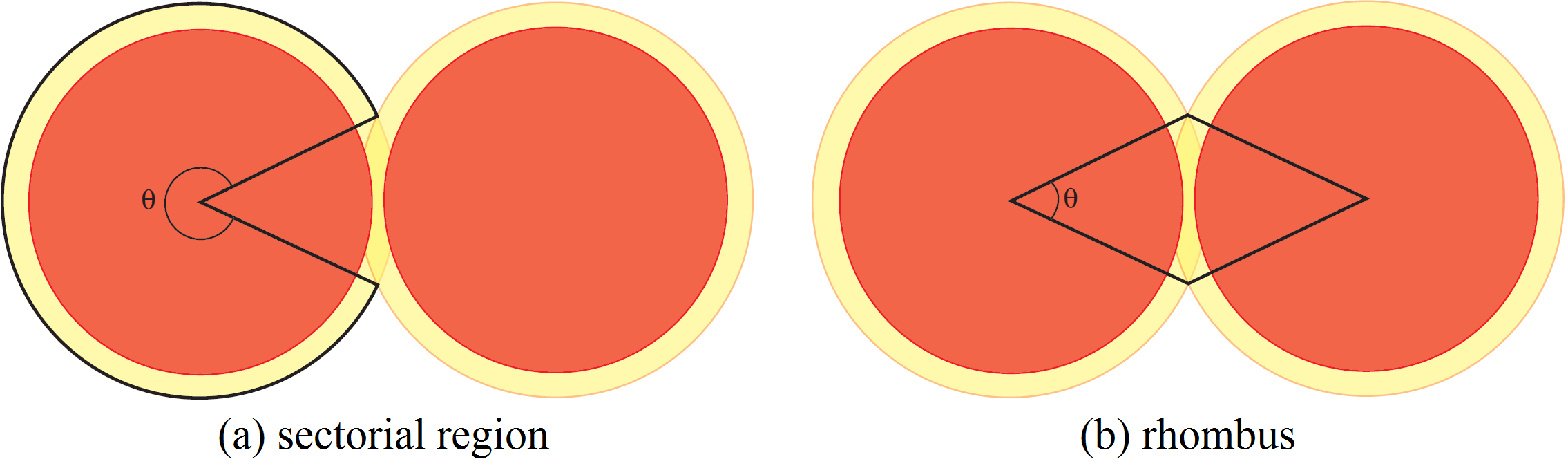
Here is a clever idea, which goes back to the Norwegian mathematician, Axel Thue, in 1890. We divide the plane in local regions and we show that, in all regions, the density is less that or equal to ![]() . Let us look at Figure 3. There we have three disks that could not be closer to each other. Now, let us look at the triangle with vertices at the centers of the disks. Inside this triangle, there is a small region not covered by the disks. If however we enlarge the disks by a factor
. Let us look at Figure 3. There we have three disks that could not be closer to each other. Now, let us look at the triangle with vertices at the centers of the disks. Inside this triangle, there is a small region not covered by the disks. If however we enlarge the disks by a factor ![]() , then the enlarged disks fill completely the triangle and this factor
, then the enlarged disks fill completely the triangle and this factor ![]() is the minimum attaining this goal.
is the minimum attaining this goal.
We will use this trick to divide the plane in adequate regions. We consider a packing of the plane with disks of radius ![]() . For each disk, we embed it inside a disk with same center and radius
. For each disk, we embed it inside a disk with same center and radius ![]() , which we call a large disk. Now, we can define our three regions. The first region is the complement of the union of large disks. Obviously, the density of this region is
, which we call a large disk. Now, we can define our three regions. The first region is the complement of the union of large disks. Obviously, the density of this region is ![]() . Depending on the distance between the centers of the disks, the large disks may or may not overlap. When large disks overlap, their boundary circles intersect. We join these intersection points to the centers of the disks. This process divides the large disks into sectors. There are two kinds of sectors:
. Depending on the distance between the centers of the disks, the large disks may or may not overlap. When large disks overlap, their boundary circles intersect. We join these intersection points to the centers of the disks. This process divides the large disks into sectors. There are two kinds of sectors:
- sectors in which the large disk has no overlapping with another large disk (see Figure 4 (a)). In any such sector the density is then equal to
![Rendered by QuickLaTeX.com \[\frac{1}{c^2}=\frac{3}{4};\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-7a5b412bf3acabb8882fdc0cf1c6347e_l3.png)
- sectors in which the large disks overlap as in Figure 4 (b). We take these sectors by pairs as in the figure. The union of the two sectors is a rhombus and we need only consider the density inside this rhombus. Since the distance between the centers of the disks is at least
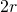 because the disks do not overlap, a calculation shows that the maximum angle of the sectors is
because the disks do not overlap, a calculation shows that the maximum angle of the sectors is 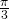 . Let
. Let 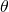 be the angle of the sector. The density inside of the rhombus depends on
be the angle of the sector. The density inside of the rhombus depends on 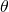 : it is given by the quotient of the areas of the two sectors of the disks by the area of the rhombus. Each sector of a disk has area
: it is given by the quotient of the areas of the two sectors of the disks by the area of the rhombus. Each sector of a disk has area 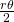 . Hence, the area covered by the disks inside the rhombus is
. Hence, the area covered by the disks inside the rhombus is 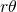 . The area of a rhombus of side
. The area of a rhombus of side 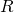 and angle
and angle 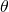 is found by decomposing the rhombus into triangles. It is equal to:
is found by decomposing the rhombus into triangles. It is equal to: 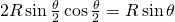 . Hence the density is
. Hence the density is
![Rendered by QuickLaTeX.com \[\mu(\theta)=\frac{r^2\theta}{R^2\sin\theta}=\frac{3\theta}{4\sin\theta}.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-90f24f10ca630f0e9d01b943b639c102_l3.png)
It suffices to study the function
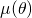 on
on ![Rendered by QuickLaTeX.com [0,\frac{\pi}3]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-97108dd255a2234a8ad4dd9ed1cb498f_l3.png) and to see that it attains its maximum at
and to see that it attains its maximum at 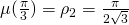 . Indeed,
. Indeed, 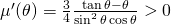 since
since 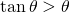 .
.
This proof is extremely elegant. Let us examine it in detail some of its features. The best density is ![]() . It is also the best density locally in each of the regions of the plane we have considered.
. It is also the best density locally in each of the regions of the plane we have considered.
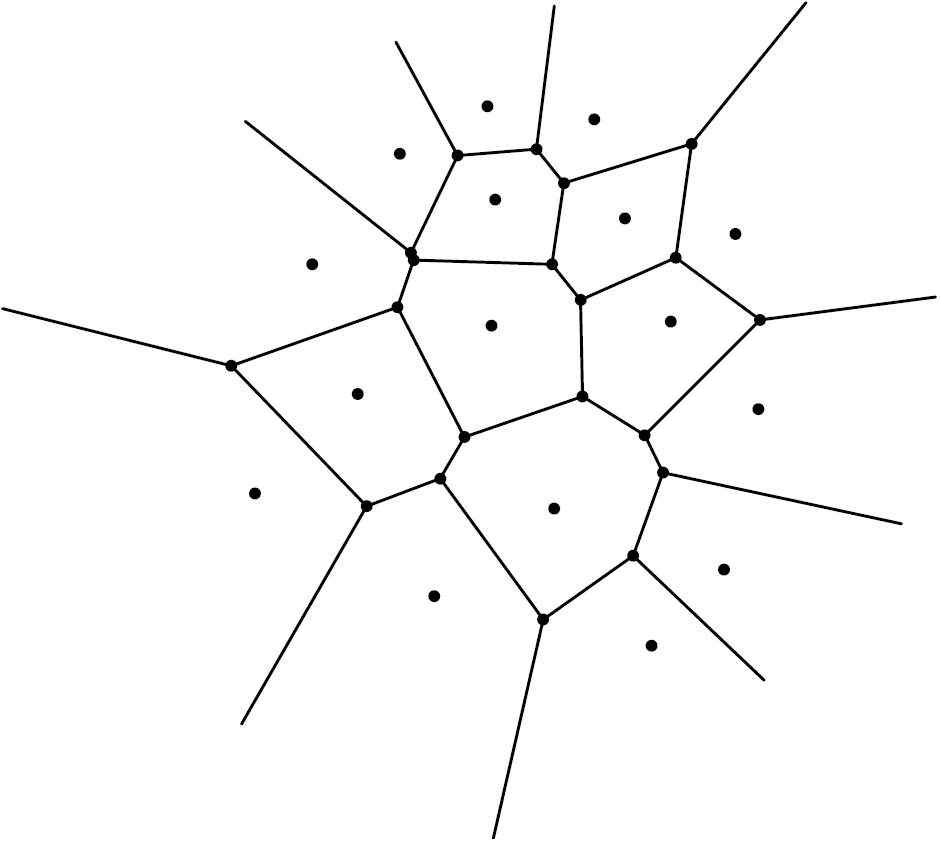
There is another way to partition the plane into regions. It is the Voronoi diagram of the set of centers of the disks. Considering a set ![]() of points in the plane, the Voronoi diagram of
of points in the plane, the Voronoi diagram of ![]() is the partition of the plane into regions, one attached to each point
is the partition of the plane into regions, one attached to each point ![]() of
of ![]() , such that the region attached to a given point
, such that the region attached to a given point ![]() is the set of points in the plane that are closer to
is the set of points in the plane that are closer to ![]() than to any other point
than to any other point ![]() of
of ![]() . These regions are called Voronoi cells. Given that the mediatrix of a segment
. These regions are called Voronoi cells. Given that the mediatrix of a segment ![]() is the geometric locus of points that are equidistant to
is the geometric locus of points that are equidistant to ![]() and
and ![]() , it is not surprising that the Voronoi diagram of a set of points looks like Figure 5, with a common side between a pair of adjacent Voronoi cells being given by a line segment of the mediatrix of the points of
, it is not surprising that the Voronoi diagram of a set of points looks like Figure 5, with a common side between a pair of adjacent Voronoi cells being given by a line segment of the mediatrix of the points of ![]() attached to the two cells.
attached to the two cells.
When we have a packing of disks in the plane, it is natural to look at the Voronoi diagram of the set of centers of the disks. Let us now come back to the two examples of Figure 2. On the left, the Voronoi cells are squares. On the right, they are hexagons, and the density of each disk inside its hexagonal Voronin cell is exactly equal to ![]() . Note that, if we surround a given disk with non overlapping disks of the same radius, the Voronoi cell with minimum area is the circumscribed hexagon.
. Note that, if we surround a given disk with non overlapping disks of the same radius, the Voronoi cell with minimum area is the circumscribed hexagon.
3. The three-dimensional case.
3.1. The difficulty of the problem.
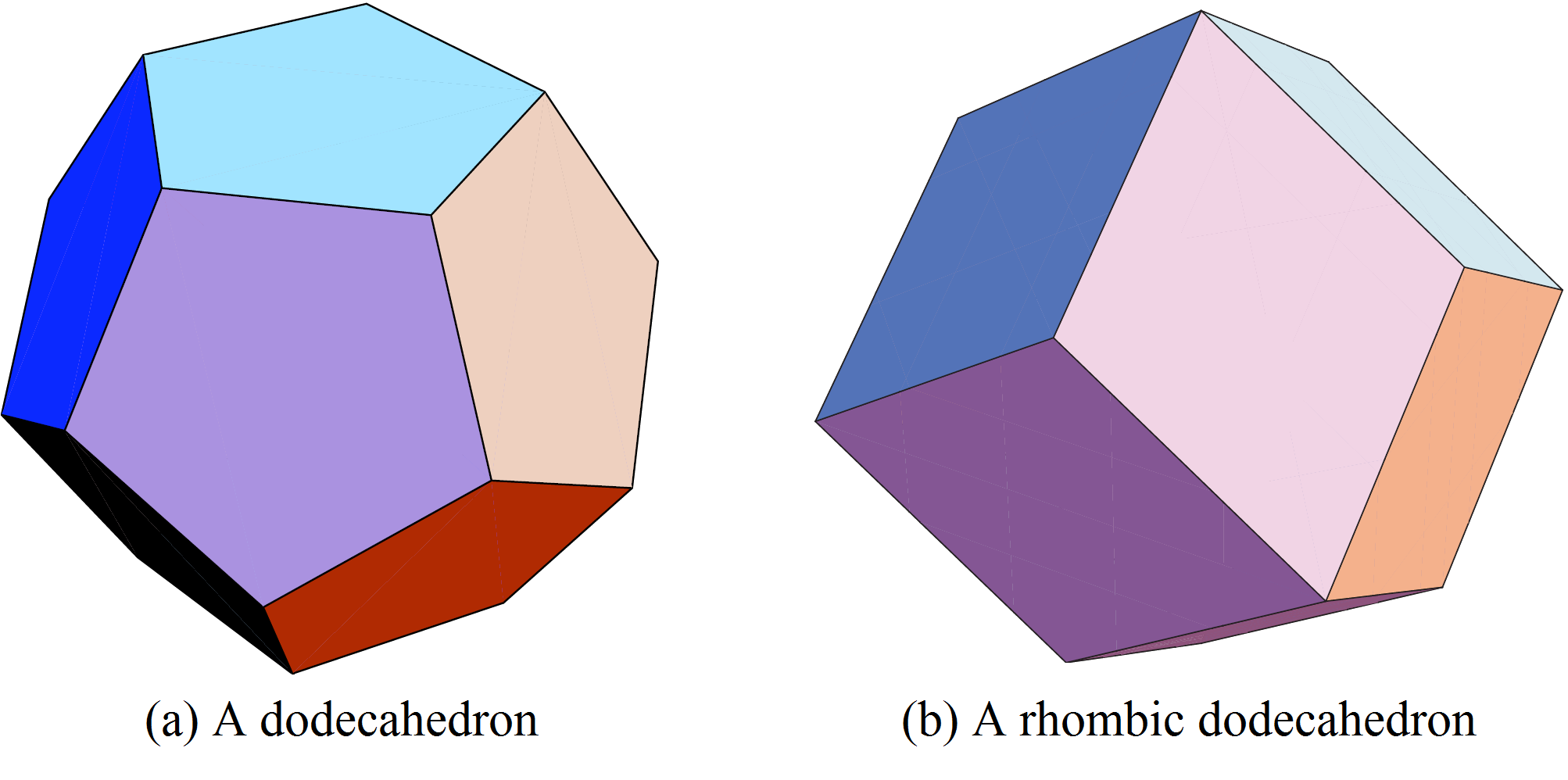
It is natural to try to generalize this idea to the three-dimensional case. The Voronoi diagram can be defined as before. Its closed cells are convex polyhedra. Let us surround a sphere by tangent spheres. We can place ![]() spheres. But, in opposition to the planar case, there remains room around the first sphere. We can try to move around the
spheres. But, in opposition to the planar case, there remains room around the first sphere. We can try to move around the ![]() tangent spheres, and see if we could place a
tangent spheres, and see if we could place a ![]() -th one. It has been proved by Thomas Hales that this is not possible. But there are many non equivalent ways to place
-th one. It has been proved by Thomas Hales that this is not possible. But there are many non equivalent ways to place ![]() spheres tangent to a given one and they do not produce Voronoi cells of the same volume! The optimal configuration to minimize the volume of the Voronoi cell is that the
spheres tangent to a given one and they do not produce Voronoi cells of the same volume! The optimal configuration to minimize the volume of the Voronoi cell is that the ![]() spheres be tangent to the original sphere at the vertices of the inscribed dodecahedron (Figure 6 (a)). This was conjectured by Fejer Tóth in the 1940’s and finally proved by an undergraduate student, Sean McLaughlin, in 1999!
spheres be tangent to the original sphere at the vertices of the inscribed dodecahedron (Figure 6 (a)). This was conjectured by Fejer Tóth in the 1940’s and finally proved by an undergraduate student, Sean McLaughlin, in 1999!
Then the Voronoi cell of the given sphere is a circumscribed dodecahedron to the sphere. It is possible to calculate the density of the sphere inside its Voronoi cell. It is inferior to the density of the packing of oranges at the fruit market! So can we do better?
No!
Because it is impossible to fill the space with non overlapping dodecahedra: we necessarily have empty space between them. Hence we see that the three-dimensional case is much more difficult than the two-dimensional case, because the local optimal solution does not coincide with the global optimal solution.
For the optimal solution whose geometry we will study in the next section, the centers of the spheres are placed at the points of the face-centered cubic lattice. The corresponding Voronoi cells are rhombic dodecahedra (see Figure 6 (b)).
Rhombic dodecahedra can tessellate space in a regular way, and such tessellations have been observed in crystallography.
The proof of the optimality of this packing has been achieved by Thomas Hales with the help of his graduate student Samuel Ferguson in 1998 (the complete proof was only published in 2006). The proof, a computer assisted proof, is a real tour-de-force. While we cannot mimic the proof of the two-dimensional case, the spirit remains the same: the proof consists in decomposing the space in regions of a finite number of types and to compute the density in each type of region. The (huge) program is available on the web for those who would like to study or check it.
3.2. The geometry of the optimal packing.
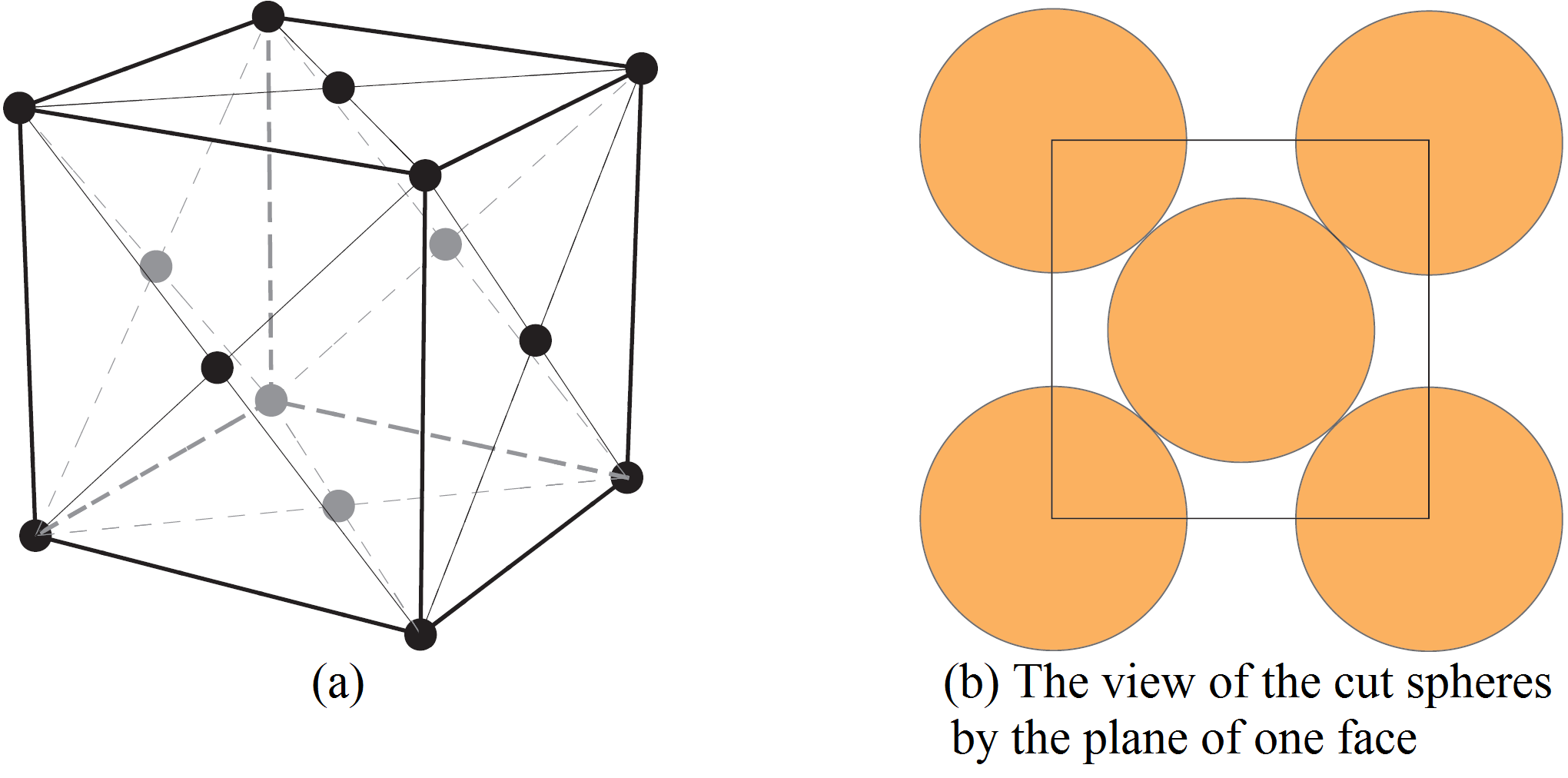
Imagine a tessellation of the three-dimensional space with cubes. Now, for each cube, we place one sphere centered at each vertex and one sphere centered at the center of each face as in
We take the radius of the spheres as large as possible so that the spheres do not intersect. If ![]() is the length of an edge of the cube, then it is clear from Figure 7 (b) that the radius of the balls should be
is the length of an edge of the cube, then it is clear from Figure 7 (b) that the radius of the balls should be ![]() . From this, we can calculate the density of the packing. Indeed, for each sphere centered at a vertex, one eight of a sphere lies inside the cube. Since there are eight vertices, this adds up to the volume of one sphere. For each sphere centered at the center of a face, half of it lies inside the cube. Since there are six faces, this adds up to the volume of three spheres. Hence, the density is the volume of four spheres divided by the volume of the cube. The volume of each sphere is
. From this, we can calculate the density of the packing. Indeed, for each sphere centered at a vertex, one eight of a sphere lies inside the cube. Since there are eight vertices, this adds up to the volume of one sphere. For each sphere centered at the center of a face, half of it lies inside the cube. Since there are six faces, this adds up to the volume of three spheres. Hence, the density is the volume of four spheres divided by the volume of the cube. The volume of each sphere is ![]() and the volume of the cube is
and the volume of the cube is ![]() . Hence, the density is
. Hence, the density is
![]()
How is this packing achieved? The same as when we pile oranges: we put a first planar layer of spheres as in Figure 2 (b). On top we put a second layer with a shift in one direction, for instance in the upper right direction. The third layer lies on top of the second layer with a shift in the same direction, etc. This brings one question. Could we change the direction of the shift between the different layers without changing the density? Yes, we can, but the corresponding lattice of centers will not be the cubic face-centered one. This means that the packing giving the highest density is not unique.
It is not obvious that the usual packing of oranges corresponds to the cubic face-centered lattice. Indeed, looking at Figure 7 (b), we see that we should have orthogonal lines of aligned centers of spheres. It is a good exercise of visualization to figure that these lines indeed do exist in the usual packing of oranges, but that none of them lie in horizontal planes. Indeed the plane of Figure 2 (b) is a slanted plane through the centers of three faces adjacent to a vertex of the cube of Figure 7 (a). In Figure 8 we represent the packing of four layers as in Figure 2 (b), one above the other. The two lines through centers of spheres are orthogonal.
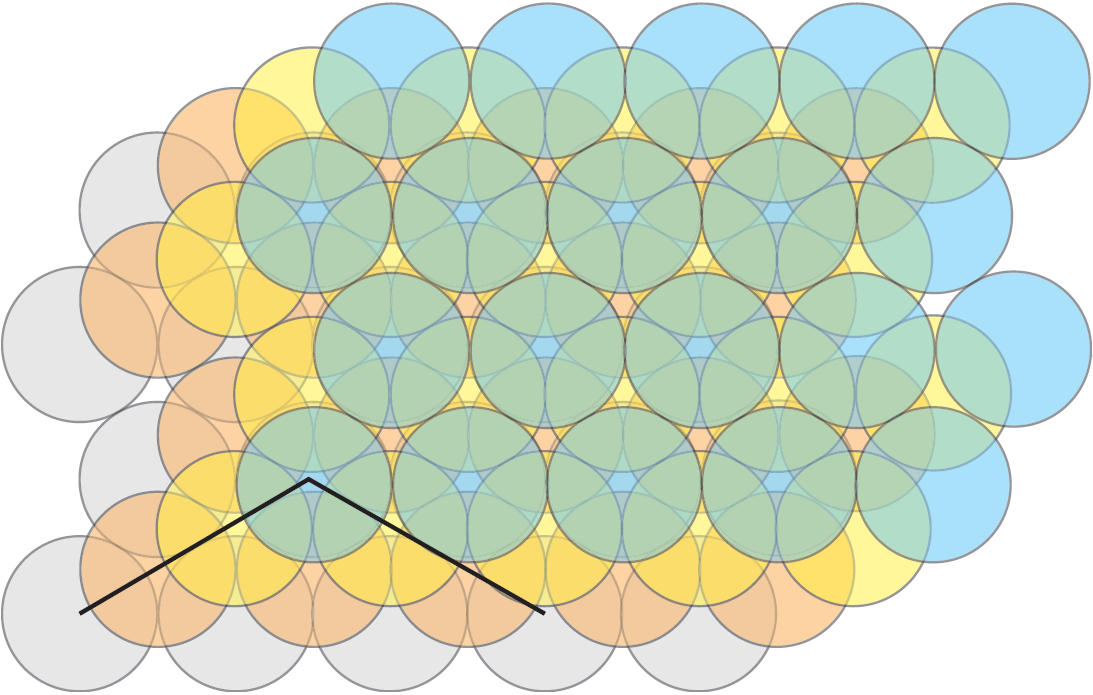
Figure 8: Four layers of spheres of the type of Figure 2 (b), one above the other and two orthogonal lines of centers.
4. Opening horizons.
4.1. Applications in crystallography.
The question of the densest packing of spheres was asked to Johannes Kepler by Thomas Harriot at the end of the 16-th century. Already at the time Harriot believed in the existence of atoms and was interested to how they are arranged around each other. When the arrangement of atoms in a material is regular, chemists say that the material is a crystal. Heavy materials, like metals, often have atoms arranged at the points of the face centered cubic lattice. Other less dense regular arrangements also exist. One of the less dense regular packing is the simple cubic packing where atoms are located at the vertices of cubes. There is only one chemical element with this configuration of atoms, namely the radioactive polonium. (More details in [4].)
4.2. Random packing.
If you pack carefully your oranges in large boxes using the face-centered cubic lattice pattern described above, then you get the density ![]() But, if you are in a hurry and you just throw them quickly in the box, what density do you get? This is what is called random packing. Of course, the density is not always the same. Indeed, if you shake your box, you will likely increase the density. But up to what point? Experiments show that the density varies from around
But, if you are in a hurry and you just throw them quickly in the box, what density do you get? This is what is called random packing. Of course, the density is not always the same. Indeed, if you shake your box, you will likely increase the density. But up to what point? Experiments show that the density varies from around ![]() (random loose packing) to a maximum of
(random loose packing) to a maximum of ![]() (random close packing). The derivation of this maximum limit was the subject of a letter in Nature in 2008 by Song, Wang and Maske [3].
(random close packing). The derivation of this maximum limit was the subject of a letter in Nature in 2008 by Song, Wang and Maske [3].
4.3. Packing other objects than spheres.
It is possible to obtain a higher density than ![]() if we change the shape of the identical objects from spheres to, for instance, ellipsoids. The paper [1] shows that the density of random close packings of spheroids with an aspect ratio like M & M candies can approach
if we change the shape of the identical objects from spheres to, for instance, ellipsoids. The paper [1] shows that the density of random close packings of spheroids with an aspect ratio like M & M candies can approach ![]() to
to ![]() and that the density for ellipsoids with some other aspect ratios can even approach
and that the density for ellipsoids with some other aspect ratios can even approach ![]() . The random packing densities are important for industry when the packing of identical objects (for instance candies or pharmaceutical pills) is automatized. In particular, the density can change during the transportation.
. The random packing densities are important for industry when the packing of identical objects (for instance candies or pharmaceutical pills) is automatized. In particular, the density can change during the transportation.
4.4. A word on higher dimensions.
In higher dimensions, the densest regular packings of hyperspheres are known up to dimension ![]() , and very little is known of the non regular packings.
, and very little is known of the non regular packings.
One application of packing of spheres in higher dimension is to produce error-correcting codes. The principle of an error-correcting code is to encode letters or words by sequences of symbols, called code words, that differ one from the other by at least ![]() symbols. Then, if less than
symbols. Then, if less than ![]() errors occur in the transmission of a code word, there exists at most one code word at a distance less than
errors occur in the transmission of a code word, there exists at most one code word at a distance less than ![]() from the received word and correction is possible. In the error-correcting codes using packing of spheres we transform letters of the code into the tuples of coordinates of centers of non overlapping spheres. If the spheres have radius
from the received word and correction is possible. In the error-correcting codes using packing of spheres we transform letters of the code into the tuples of coordinates of centers of non overlapping spheres. If the spheres have radius ![]() , then it is possible to correct less than
, then it is possible to correct less than ![]() errors.
errors.
4.5. The next questions…
It is your turn to ask them. As you have seen, there are many simple questions with important applications and whose sophisticated answers are published in some of the most important scientific journals, like Nature, Science and Annals of Mathematics.
5. The validity of computer-assisted proofs.
The proof that the densest packing of disks in the 2-dimensional case is ![]() shows that it is possible to give rigorous proofs of results where there are an infinite number of cases to analyze. It is a proof that any of you can check. But who can check the proof that
shows that it is possible to give rigorous proofs of results where there are an infinite number of cases to analyze. It is a proof that any of you can check. But who can check the proof that ![]() ? It is an enormous proof with
? It is an enormous proof with ![]() cases to analyze, and each case is so complex that it needs to be done by computer, for a total of 3 Gigabytes of computer code. Of course, the code is public. But, it took several years to the authors to produce it. So who has both the time and the skills to go through all details? For sure, there are strategies to minimize errors and Hales and Solomon have used several of these. For instance, the two authors wrote the program independently in parallel. The program could be run on different computers with different processors and compilers. The subroutines could use old software packages that have been tested for years, etc.
cases to analyze, and each case is so complex that it needs to be done by computer, for a total of 3 Gigabytes of computer code. Of course, the code is public. But, it took several years to the authors to produce it. So who has both the time and the skills to go through all details? For sure, there are strategies to minimize errors and Hales and Solomon have used several of these. For instance, the two authors wrote the program independently in parallel. The program could be run on different computers with different processors and compilers. The subroutines could use old software packages that have been tested for years, etc.
Even then, these proofs remain controversial and it is a very long decision process for the scientific community to accept such a proof. In the case of the proof of the Kepler conjecture, the (abridged) proof finally appeared in 2005 in Annals of Mathematics, one of the best mathematical journals. But the mathematical community is still in search for a more ” mathematical” proof. In parallel, mathematicians and researchers in theoretical computer science look for formal proofs, i.e. proofs in which each logical step can be checked by a computer. For instance, the purpose of the Flyspeck project is to produce a formal proof of the Kepler conjecture:
http://code.google.com/p/flyspeck/wiki/FlyspeckFactSheet
The first celebrated theorem whose proof was a computer assisted proof is the four color theorem which states that four colors suffice to color any map so that no two adjacent regions have the same color. It was proved in 1976 by Kenneth Appel and Wolfgang Haken. At the time, Annals of Mathematics would not have accepted to publish a computer assisted proof. Times have changed and the computer has revolutionized the practice of mathematics.
References.
[1] A. Donev, I. Cisse, D. Sachs, E. Variano, F. H. Stillinger, R. Connelly, S. Tarquato and P.M. Chikin, Improving the density of jammed disordered packings using ellipsoids, Science, 303 (2004), 990–993.
[2] T. Hales, Cannonballs and honeycombs, Notices of the American Mathematical Society, 47 (2000), 440–449.
[3] C. Song, P. Wang and H.A. Maske, A phase diagram for jammed matter, Nature, 453 (2008), 629–-632.
[4] G.C. Szpiro, Kepler’s conjecture, John Wiley & Sons, Inc., 2003.

Credo che il problema della migliore disposizione dei cerchi o delle sfere non sia stato affrontato nel modo giusto:
Sul piano le possibili disposizioni sono essenzialmente due ,perché la disposizione esagonale è riducibile a quella triangolare ,poiché non varia l’angolo secondo cui si dispongono sul piano i cerchi.
Nel piano abbiamo i cerchi si dispongono secondo il seno di 90° o di 60°: cioè in forma quadrata o triangolare.
Essendo il valore di sen 60° = 0,866 occorrono almeno 8 fila cerchi disposti in modo triangolare per risultare più conveniente della forma quadrata.
Nello spazio le disposizioni delle sfere rimangono le stesse :la forma quadrata dipende dal sen 45° = o,707 la forma triangolare dipende dal cos 36° = 0.809.
I valori indicano quale sia più conveniente e la disposizione quadrata risulta più stabile.
Sull’esagono si possono disporre tre sfere; quindi sulla griglia esagonale le sfere
assumeranno una disposizione orientata , uniforme solo in una direzione.
La migliore in assoluto quindi non è la disposizione esagonale.
L’ipilamento a palle di cannone rimane un aspetto marginale del problema,che tuttavia
impone di stabilire dei vincoli entro cui muoversi: vincoli che possono essere ,il contenimento o la libertà e l’uniformità dell’oggetto.