Vignette écrite par Christiane Rousseau.
Vignette écrite par Christiane Rousseau.
Dans cette vignette, nous allons découvrir, en commençant avec un petit jeu, l’un des plus puissants théorèmes des mathématiques, à savoir le théorème du point fixe de Banach. Ce théorème a de fantastiques applications aussi bien en mathématiques que dans d’autres domaines. Dans la troisième partie de cet article nous verrons une fascinante application en compression d’images.
Mais commençons avec notre jeu, et regardons de plus près le couvercle d’une boîte de Vache Qui Rit.
La boucle d’oreille droite de la Vache est encore une boîte de Vache Qui Rit. A chaque point du couvercle, on peut associer le point correspondant sur la boucle d’oreille droite. On obtient bien sûr une fonction du couvercle dans lui-même, que l’on appelle ![]() . Par exemple, on associe l’extrémité du menton de la Vache à l’extrémité du menton de la petite vache de la boucle d’oreille. On associe le centre de l’œil droit de la vache au centre de l’œil droit de la petite vache de la boucle d’oreille, etc. Et voilà maintenant la question: Y a-t-il un point qui est envoyé sur lui-même par ce procédé? Un tel point, s’il existe, sera appelé un point fixe. Si un point fixe existe, alors alors ce n’est pas un des points dont nous avons parlé précédemment. De plus, si un point fixe existe, alors il doit être dans la boucle d’oreille droite. Mais cette boucle d’oreille est envoyée sur la boucle d’oreille de la petite vache, etc. Visuellement, on devine que ces boucles d’oreilles droites emboîtées semblent converger vers un point, que l’on appelle
. Par exemple, on associe l’extrémité du menton de la Vache à l’extrémité du menton de la petite vache de la boucle d’oreille. On associe le centre de l’œil droit de la vache au centre de l’œil droit de la petite vache de la boucle d’oreille, etc. Et voilà maintenant la question: Y a-t-il un point qui est envoyé sur lui-même par ce procédé? Un tel point, s’il existe, sera appelé un point fixe. Si un point fixe existe, alors alors ce n’est pas un des points dont nous avons parlé précédemment. De plus, si un point fixe existe, alors il doit être dans la boucle d’oreille droite. Mais cette boucle d’oreille est envoyée sur la boucle d’oreille de la petite vache, etc. Visuellement, on devine que ces boucles d’oreilles droites emboîtées semblent converger vers un point, que l’on appelle ![]() , et
, et ![]() est un candidat pour notre solution.
est un candidat pour notre solution.
Commençons maintenant avec un point quelconque, par exemple l’extrémité du menton de la vache, et appelons-le ![]() . Alors
. Alors ![]() est envoyé sur
est envoyé sur ![]() , qui est l’extrémité du menton de la petite vache sur la boucle d’oreille droite. Alors
, qui est l’extrémité du menton de la petite vache sur la boucle d’oreille droite. Alors ![]() est envoyé sur
est envoyé sur ![]() , qui est l’extrémité du menton de la vache de la boucle d’oreille droite de la petite vache, etc. On remarque trois choses:
, qui est l’extrémité du menton de la vache de la boucle d’oreille droite de la petite vache, etc. On remarque trois choses:
- On pourrait continuer ce procédé indéfiniment et créer ainsi une suite
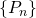 , où
, où 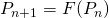 .
.
- Visuellement, seul un nombre fini de points semblent distincts, et les autres ne peuvent pas être distingués les uns des autres. Bien sûr, on peut zoomer et voir plus de points. Mais peu importe la puissance du zoom, on ne distinguera qu’un nombre fini de points distincts, et les autres sembleront superposés.
- Cette suite semble converger vers le point
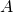 défini précédemment.
défini précédemment.
Si nous avions pris un autre point ![]() et construit la suite
et construit la suite ![]() , où
, où ![]() , nous pourrions voir que la suite
, nous pourrions voir que la suite ![]() semble également converger vers le point
semble également converger vers le point ![]() . En fait on peut remarquer que cela vient du fait que le singleton
. En fait on peut remarquer que cela vient du fait que le singleton ![]() est l’intersection de toutes les boucles d’oreilles emboîtées, dont le diamètre tend vers
est l’intersection de toutes les boucles d’oreilles emboîtées, dont le diamètre tend vers ![]() .
.
Que nous dira le théorème du point fixe de Banach? Il nous dira que, en effet, la fonction ![]() a un unique point fixe, c’est-à-dire il existe un unique point
a un unique point fixe, c’est-à-dire il existe un unique point ![]() du plan tel que
du plan tel que ![]() . De plus, il établira également que si nous prenons un point
. De plus, il établira également que si nous prenons un point ![]() quelconque et que nous construisons la suite
quelconque et que nous construisons la suite ![]() , où
, où ![]() , alors la suite
, alors la suite ![]() convergera vers
convergera vers ![]() .
.
Pourquoi? Est-ce que cela peut arriver pour n’importe quelle fonction ![]() ? Bien sûr que non. Par exemple, une translation du plan n’a pas de point fixe. Et la fonction
? Bien sûr que non. Par exemple, une translation du plan n’a pas de point fixe. Et la fonction ![]() a deux points fixes, à savoir
a deux points fixes, à savoir ![]() La fonction
La fonction ![]() de notre jeu a une propriété spéciale. C’est une contraction. En effet, l’image de la fonction est plus petite que son ensemble de définition. Si deux points
de notre jeu a une propriété spéciale. C’est une contraction. En effet, l’image de la fonction est plus petite que son ensemble de définition. Si deux points ![]() et
et ![]() sont écartés d’une certaine distance, alors leurs images
sont écartés d’une certaine distance, alors leurs images ![]() et
et ![]() seront plus proches l’un de l’autre que ne le sont
seront plus proches l’un de l’autre que ne le sont ![]() et
et ![]() . Cette affirmation a du sens, car dans
. Cette affirmation a du sens, car dans ![]() on peut mesurer la distance entre deux points. C’est parce que
on peut mesurer la distance entre deux points. C’est parce que ![]() est un espace métrique. C’est le fait que
est un espace métrique. C’est le fait que ![]() soit une contraction qui garantit que lorsque l’on construit la suite
soit une contraction qui garantit que lorsque l’on construit la suite ![]() , alors peu importe le recul depuis lequel on regarde la suite (c’est-à-dire si on regarde la suite de loin, ou de près, ou à travers un microscope ou un microscope électronique), alors à partir d’un rang
, alors peu importe le recul depuis lequel on regarde la suite (c’est-à-dire si on regarde la suite de loin, ou de près, ou à travers un microscope ou un microscope électronique), alors à partir d’un rang ![]() qui dépend du recul choisi, tous les éléments
qui dépend du recul choisi, tous les éléments ![]() ,
, ![]() , de la suite deviennent indistincts. Deux éléments sont distincts si la distance qui les séparent est plus grande qu’un certain seuil. Nous verrons dans la prochaine partie qu’une suite ayant cette propriété est appelée une suite de Cauchy. Dans
, de la suite deviennent indistincts. Deux éléments sont distincts si la distance qui les séparent est plus grande qu’un certain seuil. Nous verrons dans la prochaine partie qu’une suite ayant cette propriété est appelée une suite de Cauchy. Dans ![]() , toute suite de Cauchy est une suite convergente. On dit que
, toute suite de Cauchy est une suite convergente. On dit que ![]() est un espace métrique complet.
est un espace métrique complet.
1. Le théorème du point fixe de Banach
Nous avons maintenant tous les ingrédients pour le cas général, et nous pouvons énoncer le théorème.
Théorème (du point fixe de Banach). Soit ![]() un espace métrique complet dans lequel la distance entre deux points
un espace métrique complet dans lequel la distance entre deux points ![]() et
et ![]() est notée
est notée ![]() . Et soit
. Et soit ![]() une contraction, c’est-à-dire il existe
une contraction, c’est-à-dire il existe ![]() tel que pour tout
tel que pour tout ![]() , alors
, alors
![]()
Alors ![]() a un unique point fixe, c’est-à-dire il existe un unique
a un unique point fixe, c’est-à-dire il existe un unique ![]() tel que
tel que ![]() .
.
Nous allons définir chaque terme apparaissant dans cet énoncé. Cette partie est plus formelle et peut être sautée si vous préférez vous concentrer sur les applications fascinantes.
Nous savons ce qu’est la distance entre deux points ![]() et
et ![]() dans
dans ![]() . Comment la généraliser à un ensemble
. Comment la généraliser à un ensemble ![]() ?
?
Définition. une distance sur un ensemble ![]() est une fonction
est une fonction ![]() vérifiant
vérifiant
- Pour tout
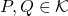 ,
, 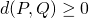 ;
;
-
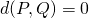 si et seulement si
si et seulement si 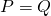 ;
;
- Pour tout
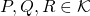 ,
, 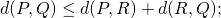 (inégalité triangulaire.)
(inégalité triangulaire.)
Nous savons que ces propriétés sont vérifiées pour la distance euclidienne usuelle dans ![]() .
.
Nous rappelons maintenant la définition d’une suite de Cauchy, qui est la formalisation du concept de suite pour laquelle, peu importe quel seuil de précision on choisit, après un nombre fini d’éléments, tous les autres éléments deviennent indistincts. On rappelle également la définition d’une suite convergente.
Définition.
- Une suite
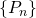 d’éléments d’un espace métrique
d’éléments d’un espace métrique 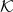 est une suite de Cauchy si pour tout
est une suite de Cauchy si pour tout 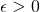 , il existe
, il existe 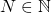 tel que pour tout
tel que pour tout  , alors
, alors
![Rendered by QuickLaTeX.com \[d(P_n,P_m)<\epsilon.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-1c97f4794c43d7a0ea39241b9d7b70f0_l3.png)
- Une suite
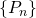 d’éléments d’un espace métrique
d’éléments d’un espace métrique 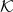 converge vers une limite
converge vers une limite 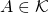 si pour tout
si pour tout 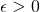 , il existe
, il existe 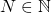 tel que pour tout
tel que pour tout 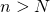 , alors
, alors
![Rendered by QuickLaTeX.com \[d(P_n,A)<\epsilon.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-15d19b7399d98032c767b201bb2322a3_l3.png)
Définition. Un espace métrique ![]() est un espace métrique complet si toute suite de Cauchy
est un espace métrique complet si toute suite de Cauchy ![]() d’éléments de
d’éléments de ![]() converge vers un élément
converge vers un élément ![]() de
de ![]() .
.
Comment démontrer le théorème du point fixe de Banach? L’unicité du point fixe est facile. En effet, supposons que ![]() et
et ![]() soient deux points fixes. Alors
soient deux points fixes. Alors ![]() et
et ![]() . De plus, puisque
. De plus, puisque ![]() est une contraction,
est une contraction,
![]()
et donc, ![]() . La seule solution est
. La seule solution est ![]() , c’est-à-dire
, c’est-à-dire ![]() .
.
Pour l’existence, l’idée de la preuve est également simple: Nous l’avons déjà trouvée dans notre jeu avec la Vache Qui Rit! Prenons un point ![]() quelconque et construisons (comme précédemment) la suite
quelconque et construisons (comme précédemment) la suite ![]() , où
, où ![]() . Ainsi cette suite est une suite de Cauchy et sa limite est un point fixe. (Bien évidemment, démontrer ces deux assertions requiert du travail, mais nous omettrons les détails techniques. Ce qui importe est le fait que la preuve soit la même dans le cas général d’un espace métrique complet compliqué que dans le cas simple
. Ainsi cette suite est une suite de Cauchy et sa limite est un point fixe. (Bien évidemment, démontrer ces deux assertions requiert du travail, mais nous omettrons les détails techniques. Ce qui importe est le fait que la preuve soit la même dans le cas général d’un espace métrique complet compliqué que dans le cas simple ![]() .)
.)
L’idée de la preuve n’est pas seulement simple et intuitive, mais également très puissante. Elle nous fournit une façon de construire numériquement le point fixe ![]() . Ce qui explique que de nombreuses applications de ce théorème puissent aussi bien être trouvées du côté théorique que du côté appliqué.
. Ce qui explique que de nombreuses applications de ce théorème puissent aussi bien être trouvées du côté théorique que du côté appliqué.
2. Les applications en analyse
Une des application théoriques très importantes du théorème du point fixe de Banach est la preuve de l’existence et de l’unicité de solutions d’équations différentielles suffisamment régulières. Dans cette application, l’espace complet ![]() est un ensemble de fonctions, et la fonction
est un ensemble de fonctions, et la fonction ![]() transforme une fonction en une autre (on dit souvent que
transforme une fonction en une autre (on dit souvent que ![]() est un opérateur). L’astuce consiste à démontrer que la solution de l’équation différentielle, si elle existe, est un point fixe de l’opérateur
est un opérateur). L’astuce consiste à démontrer que la solution de l’équation différentielle, si elle existe, est un point fixe de l’opérateur ![]() .
.
Vous avez peut-être étudié des équations différentielles simples et appris des astuces pour trouver des formules pour les solutions. Ces équations différentielles sont l’exception, et pour la plupart des équations différentielles il n’existe pas de formule pour la solution. D’où l’importance d’un théorème affirmant l’existence et l’unicité d’une solution. Vous ne devriez pas être surpris qu’il soit impossible de donner une formule pour les solutions de la plupart des équations différentielles. En effet, considérons l’équation simple
![]()
Sa solution est donnée par
![]()
Vous vous souvenez peut-être de vos cours de probabilité ou de statistiques qu’il n’existe pas de formule pour la primitive de la fonction ![]() , et donc pourquoi on utilise des tableaux lorsque l’on étudie la loi normale.
, et donc pourquoi on utilise des tableaux lorsque l’on étudie la loi normale.
3. Application à la compression d’images
Le meilleur moyen de sauvegarder une image est d’enregistrer la couleur de chaque pixel. Il y a deux problèmes avec cette méthode:
- Elle requiert une énorme quantité de mémoire.
- Si on essaye d’agrandir l’image, par exemple en l’utilisant sur une grande affiche, alors les pixels deviendront de grands carrés et nous n’aurons pas assez d’informations pour compléter les détails de ces carrés.
Quel est le principe de la compression d’images? C’est d’encoder moins d’informations que l’image originale, mais en le faisant de manière intelligente, de sorte que l’oeil ne puisse pas voir que l’image observée est détériorée. Internet a augmenté le besoin de bon systèmes de compression d’images. En effet, les images ralentissent de façon significative la navigation sur internet. 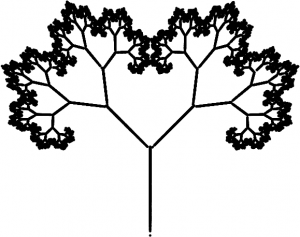 Ainsi, pour naviguer sur la Toile, il faut des images encodées dans des fichiers aussi petits que possible. Lorsque vous regardez cette image sur votre écran d’ordinateur, vous ne pouvez pas voir qu’elle a été détériorée. Mais si vous essayez de l’agrandir ou de l’imprimer sur une affiche, vous pourriez voir immédiatement que la qualité est mauvaise.
Ainsi, pour naviguer sur la Toile, il faut des images encodées dans des fichiers aussi petits que possible. Lorsque vous regardez cette image sur votre écran d’ordinateur, vous ne pouvez pas voir qu’elle a été détériorée. Mais si vous essayez de l’agrandir ou de l’imprimer sur une affiche, vous pourriez voir immédiatement que la qualité est mauvaise.
Il existe plusieurs procédés de compression d’images et le plus commun est le JPEG, qui est devenu standard pour les images numériques. L’encodage d’une image en format JPEG est aussi un algorithme mathématique.
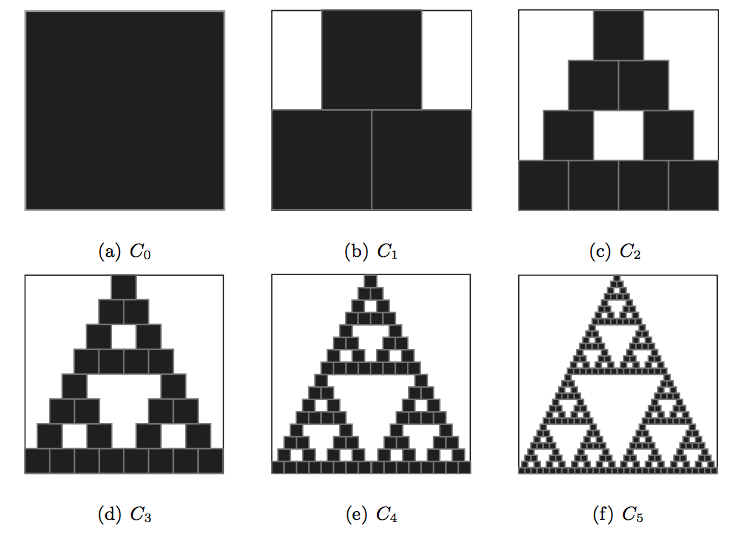
 Dans cette vignette nous allons nous concentrer sur une autre méthode, qui est restée plus expérimentale. Ce procédé, découvert par Barnsley, a été appelé système de fonctions itérées. L’idée sous-jacente de la méthode est d’approcher une image par des objets géométriques. Pour avoir suffisamment d’objets disponibles, on ne se limitera pas aux objets géométriques usuels comme les droites et les courbes, mais on utilisera également des figures fractales complexes comme la fougère ou le tapis de Sierpiński (voir la figure à gauche).
Dans cette vignette nous allons nous concentrer sur une autre méthode, qui est restée plus expérimentale. Ce procédé, découvert par Barnsley, a été appelé système de fonctions itérées. L’idée sous-jacente de la méthode est d’approcher une image par des objets géométriques. Pour avoir suffisamment d’objets disponibles, on ne se limitera pas aux objets géométriques usuels comme les droites et les courbes, mais on utilisera également des figures fractales complexes comme la fougère ou le tapis de Sierpiński (voir la figure à gauche).
 Nous allons expliquer l’idée du procédé de compression sur le tapis de Sierpiński à gauche. Il semble compliqué à priori. Comment le stocker dans la mémoire d’un ordinateur de façon économique? Le mieux est d’enregistrer un programme qui le reconstruira lorsqu’on en aura besoin.
Nous allons expliquer l’idée du procédé de compression sur le tapis de Sierpiński à gauche. Il semble compliqué à priori. Comment le stocker dans la mémoire d’un ordinateur de façon économique? Le mieux est d’enregistrer un programme qui le reconstruira lorsqu’on en aura besoin.
Et pour construire ce programme on a besoin de comprendre ce qui caractérise cet objet géométrique. Observons notre tapis de Sierpiński: c’est l’union de trois tapis de Sierpiński (c’est-à-dire 3 copies de lui-même), qui sont deux fois plus petits (en largeur et en hauteur). En effet, en partant du tapis de Sierpiński, on peut en construire un second avec le procédé suivant:
- On réduit le tapis de Sierpiński de moitié en partant du sommet inférieur gauche.
- On fabrique une seconde copie de ce demi tapis de Sierpiński et on le colle à droite du premier.
- On fabrique une troisième copie de ce demi tapis de Sierpiński et on le colle au-dessus des deux autres.
La seconde figure que nous avons construite est identique au tapis de Sierpiński initial. Donc, le tapis de Sierpiński est un point fixe de ce procédé.
Écrivons cela en termes mathématiques. Remarquons que la base du tapis de Sierpiński est égale à sa hauteur. On peut donc construire un repère dont l’origine se situe au sommet inférieur gauche du tapis de Sierpiński, et dont les unités des axes sont telles que la base et la hauteur ont toute deux pour longueur 1. On construit également les transformations affines suivantes définies sur ![]() :
:
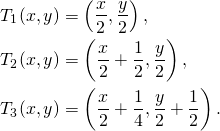
Si ![]() est le tapis de Sierpiński, alors on a
est le tapis de Sierpiński, alors on a
![]()
Y a-t-il d’autres sous-ensembles ![]() du plan qui ont la même propriété, à savoir
du plan qui ont la même propriété, à savoir
(1) ![]()
Nous allons faire une expérience et voir que non! Nous aurons donc caractérisé notre tapis de Sierpiński comme étant le seul sous ensemble ![]() du plan tel que (1) soit satisfaite. Qu’avons nous fait? Nous avons construit une fonction qui associe à un sous ensemble
du plan tel que (1) soit satisfaite. Qu’avons nous fait? Nous avons construit une fonction qui associe à un sous ensemble ![]() du plan le sous ensemble
du plan le sous ensemble ![]() . Appelons cette fonction
. Appelons cette fonction ![]() . Elle est définie par
. Elle est définie par
(2) ![]()
et nous avons vu que ![]() , i.e.
, i.e. ![]() est un point fixe de cette fonction.
est un point fixe de cette fonction.
Nous avons dit que nous allions faire une expérience pour montrer que le tapis de Sierpiński est le seul point fixe de cette fonction. Essayons avec un carré ![]() comme dans la Figure 1(a). Son image est
comme dans la Figure 1(a). Son image est ![]() (Figure 1(b)). On applique le même procédé à
(Figure 1(b)). On applique le même procédé à ![]() et on obtient
et on obtient ![]() ,
, ![]() –
–![]() . (Figure 1 (c)-(f)).
. (Figure 1 (c)-(f)).
On observe trois choses:
- Aucun des ensembles
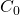 , …,
, …, 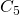 n’est un point fixe pour
n’est un point fixe pour 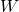 .
.
- Nous pourrions continuer indéfiniment ce procédé, et ainsi obtenir une suite infinie d’ensembles
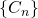 , où
, où 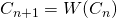 .
.
- La suite
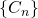 semble converger rapidement vers le tapis de Sierpiński. En effet, notre oeil ne peut distinguer
semble converger rapidement vers le tapis de Sierpiński. En effet, notre oeil ne peut distinguer 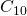 de
de 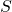 . Donc, à la place de
. Donc, à la place de 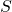 sur notre image, le programme de reconstruction peut simplement produire
sur notre image, le programme de reconstruction peut simplement produire 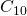 . Et si une meilleure résolution était nécessaire, on utiliserait le même programme en lui demandant de s’arrêter à
. Et si une meilleure résolution était nécessaire, on utiliserait le même programme en lui demandant de s’arrêter à 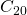 , ou
, ou 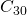 . Le même minuscule programme peut reconstruire
. Le même minuscule programme peut reconstruire 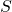 avec une précision arbitraire!
avec une précision arbitraire!
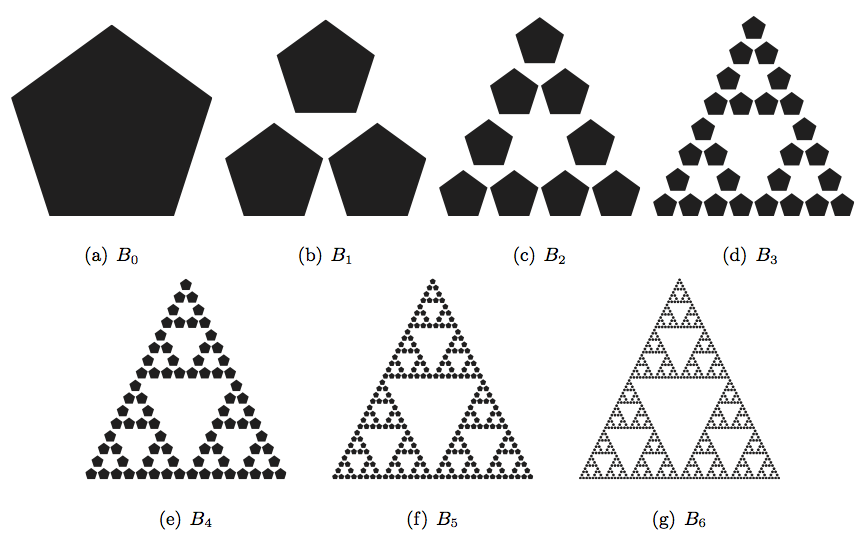
De plus, on peut refaire cette expérience et voir que cela fonctionne avec n’importe quel ensemble de départ! Un deuxième exemple avec un pentagone est visible dans la Figure 2. Les mêmes remarques 1, 2 et 3 comme ci-dessus peuvent s’appliquer à cet exemple.
Nous avons vu que le théorème du point fixe de Banach s’applique aux contractions des espaces métriques complets. En (2) nous avons défini la fonction ![]() sur les sous-espaces du plan. Pour l’espace métrique, nous allons prendre
sur les sous-espaces du plan. Pour l’espace métrique, nous allons prendre ![]() comme étant l’ensemble des sous-ensembles (fermés) bornés du plan. Nous allons introduire une distance sur
comme étant l’ensemble des sous-ensembles (fermés) bornés du plan. Nous allons introduire une distance sur ![]() appelée la distance de Hausdorff. La définition de la distance de Hausdorff
appelée la distance de Hausdorff. La définition de la distance de Hausdorff ![]() , entre deux sous-ensembles
, entre deux sous-ensembles ![]() et
et ![]() est une formule obscure et compliquée, donc nous expliquerons cette notion d’une façon différente. Commençons par expliquer ce que nous entendons par
est une formule obscure et compliquée, donc nous expliquerons cette notion d’une façon différente. Commençons par expliquer ce que nous entendons par
![]()
(même si nous n’avons pas défini ce que ![]() signifie!). Cela veut dire que si notre oeil a une précision de
signifie!). Cela veut dire que si notre oeil a une précision de ![]() , alors il ne peut pas distinguer
, alors il ne peut pas distinguer ![]() de
de ![]() . En termes mathématiques, alors
. En termes mathématiques, alors ![]() signifie
signifie
(3) ![]()
(ici ![]() est la distance euclidienne usuelle sur
est la distance euclidienne usuelle sur ![]() .) Ceci nous permet de donner la définition indirecte suivante.
.) Ceci nous permet de donner la définition indirecte suivante.
Définition. La distance de Hausdorff entre deux ensembles fermés et bornés ![]() et
et ![]() est le minimum de tous les
est le minimum de tous les ![]() tels que (3) soit vérifiée.
tels que (3) soit vérifiée.
On peut maintenant admettre que la fonction ![]() est une contraction. En effet, supposons que
est une contraction. En effet, supposons que ![]() . Alors, on peut prouver que
. Alors, on peut prouver que ![]() . Soit
. Soit ![]() . Alors, il existe
. Alors, il existe ![]() et
et ![]() tel que
tel que ![]() Puisque
Puisque ![]() , il existe
, il existe ![]() de sorte que
de sorte que ![]() . Soit
. Soit ![]() . Alors
. Alors ![]() et
et ![]() . De même, si on commence avec
. De même, si on commence avec ![]() alors il existe
alors il existe ![]() tel que
tel que ![]() .
.
Ce procédé a été adapté à la compression de vraies images (voir [K] ou [RS]). La méthode produit des images de grande qualité lorsque l’image originale a un caractère fractal. Cependant, le niveau de compression n’est pas aussi flexible et performant qu’avec le format JPEG. De plus, le procédé d’encodage (transformant l’image en un programme censé la reconstruire) est toujours trop complexe pour avoir un intérêt pratique. Cependant, la simplicité de cette idée combinée avec sa puissance reste impressionnante et très séduisante.
4. Une application surprenante: l’algorithme PageRank
Le succès de Google en tant que moteur de recherche vient de son algorithme: l’algorithme PageRank. Dans cet algorithme, on calcule un point fixe d’un opérateur linéaire sur ![]() qui est une contraction, et ce point fixe (qui est un vecteur) engendre le classement des pages. En pratique, le point fixe (qui est un vecteur propre pour la valeur propre
qui est une contraction, et ce point fixe (qui est un vecteur) engendre le classement des pages. En pratique, le point fixe (qui est un vecteur propre pour la valeur propre ![]() ) est calculé de façon approximative par
) est calculé de façon approximative par ![]() pour
pour ![]() suffisamment grand. Nous invitons le lecteur intéressé à regarder plus en détail la vignette Comment Google fonctionne.
suffisamment grand. Nous invitons le lecteur intéressé à regarder plus en détail la vignette Comment Google fonctionne.
5. Conclusion
Nous avons vu dans cette vignette comment, en commençant par un simple jeu, on peut découvrir des idées très puissantes qui peuvent conduire à des avancées majeures pour les mathématiques et la technologie. Lorsque nous cherchons une solution unique à un problème, il est désormais normal, dans de nombreux domaines des mathématiques, d’essayer de voir si la solution au problème peut être caractérisée comme l’unique point fixe d’un opérateur construit spécialement à cette fin.
Nous avons vu que l’avantage de cette approche est que le théorème fournit une façon efficace et concrète de construire la solution comme la limite d’une suite, puisque la convergence est rapide.
L’analyse est l’étude des fonctions. Les fonctions sont généralement définies sur les nombres. En analyse à plusieurs variables, on généralise la notion de fonction aux vecteurs, qui sont des éléments de ![]() . Mais pourquoi s’arrêter aux éléments de
. Mais pourquoi s’arrêter aux éléments de ![]() ? Nous avons aussi vu que les mathématiciens aiment généraliser la notion de fonctions, et s’autorisent à les définir, par exemple, sur des ensembles d’ensembles, des ensembles de fonctions, etc. L’analyse portant sur les ensembles de fonctions est désormais devenue un chapitre important de l’analyse moderne, appelé analyse fonctionnelle, qui est standard dans les études de niveau master.
? Nous avons aussi vu que les mathématiciens aiment généraliser la notion de fonctions, et s’autorisent à les définir, par exemple, sur des ensembles d’ensembles, des ensembles de fonctions, etc. L’analyse portant sur les ensembles de fonctions est désormais devenue un chapitre important de l’analyse moderne, appelé analyse fonctionnelle, qui est standard dans les études de niveau master.
Nous vous invitons à faire le lien avec des procédés itératifs que vous avez rencontrés. Par exemple avec les procédés itératifs en dimension 1 associés aux suites de Héron pour obtenir des racines carrées. La convergence rapide des suites géométriques peut également être comprise du point de vue expliqué dans cette vignette.
Bibliographie
[B] M. F. Barnsley, Fractals everywhere, San Diego, Academic Press, 1988.
[K] J. Kominek, Advances in fractal compression for
multimedia applications, Multimedia Systems Journal, vol. 5,
n![]() 4, 1997, 255–270.
4, 1997, 255–270.
[R] C. Rousseau, Point fixe de Banach, Accromath 5, hiver-printemps 2010 (www.accromath.ca).
[R2] C. Rousseau, Comment Google fonctionne: chaînes de Markov et valeurs propres, Klein vignette (www.kleinproject.org).
[RS] C. Rousseau et Y. Saint-Aubin, Mathématiques et technologie, SUMAT Series, Springer-Verlag, 2008 .