Originating authors are Dirce Uesu Pesco and Humberto José Bortolossi.
Originating authors are Dirce Uesu Pesco and Humberto José Bortolossi.
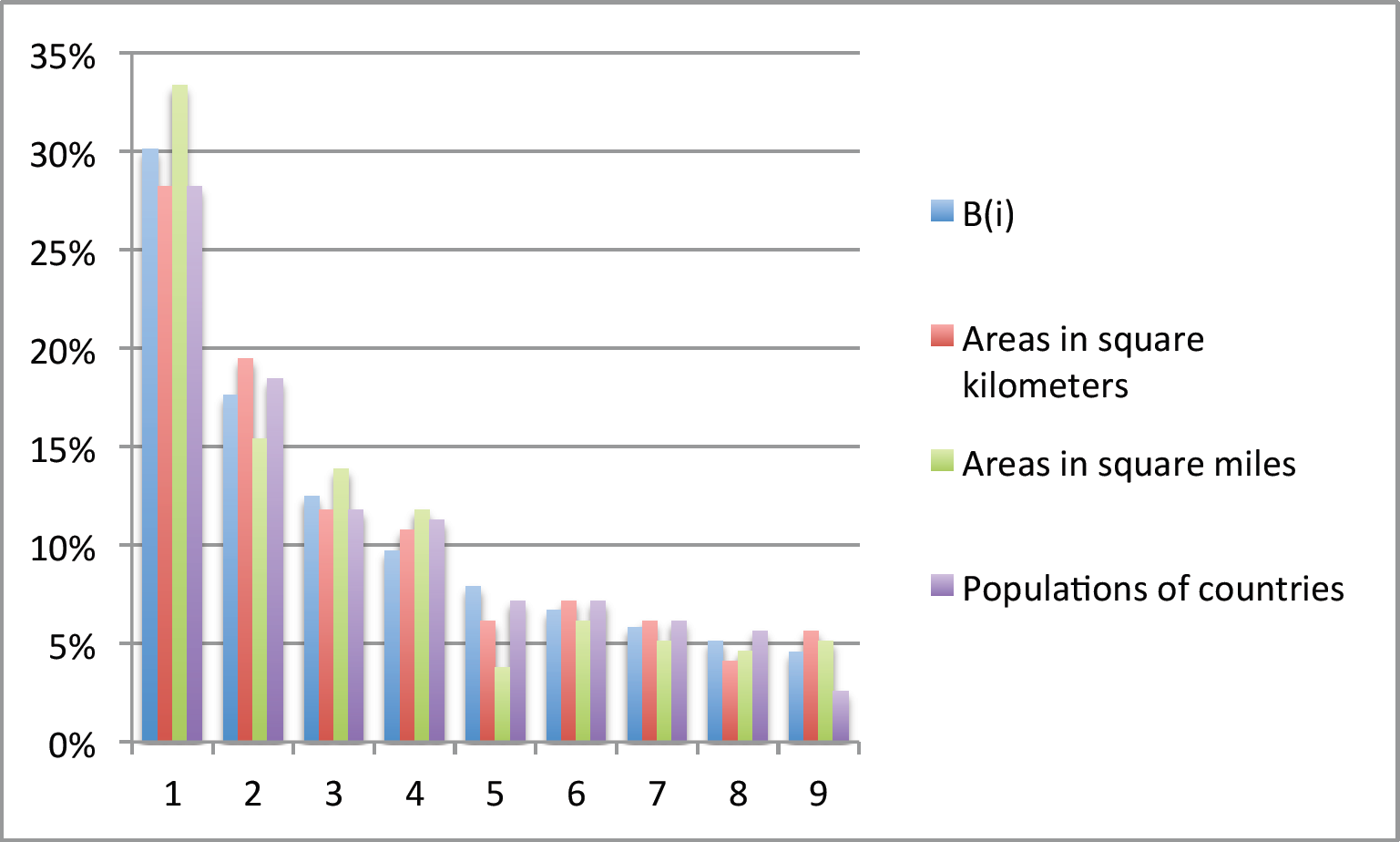
The images you see on internet pages and the photos you take with your mobile phone are examples of digital images. It is possible to represent this kind of image using matrices. For example, the small image of Felix the Cat (on the left) can be represented by a ![]() matrix whose elements are the numbers
matrix whose elements are the numbers ![]() and
and ![]() . These numbers specify the color of each pixel (a pixel is the smallest graphical element of a matricial image, which can take only one color at a time): the number
. These numbers specify the color of each pixel (a pixel is the smallest graphical element of a matricial image, which can take only one color at a time): the number ![]() indicates black, and the number
indicates black, and the number ![]() indicates white. Digital images using only two colors are called binary images or boolean images.
indicates white. Digital images using only two colors are called binary images or boolean images.
Receive notice of every new vignette.
Search
Meta