 Vignette écrite par Michèle Artigue et Ferdinando Arzarello.
Vignette écrite par Michèle Artigue et Ferdinando Arzarello.
Un quadrillage fait de carrés étant donné, il est facile de construire des carrés dont tous les sommets sont des nœuds du quadrillage. Mais est-ce possible pour d’autres polygones réguliers, par exemple pour un octogone ? La réponse est : « Non » et on peut le démontrer, pour l’octogone, de la façon suivante (Payan, 1994) :
Oublions momentanément le quadrillage. A chaque octogone régulier (c’est-à-dire un octogone dont tous les côtés et tous les angles sont égaux), on associe un second octogone construit comme indiqué sur la figure 2. Le point ![]() est l’image du point
est l’image du point ![]() par la rotation dans le sens direct de centre
par la rotation dans le sens direct de centre ![]() et d’angle
et d’angle ![]() , le point
, le point ![]() est l’image de
est l’image de ![]() par la rotation dans le sens direct de centre
par la rotation dans le sens direct de centre ![]() et d’angle
et d’angle ![]() , et ainsi de suite… On peut démontrer qu’on obtient ainsi un second polygone régulier homothétique du premier et de même centre
, et ainsi de suite… On peut démontrer qu’on obtient ainsi un second polygone régulier homothétique du premier et de même centre ![]() . Son aire est strictement inférieure à celle de l’octogone initial.
. Son aire est strictement inférieure à celle de l’octogone initial.
Revenons maintenant aux polygones convexes dont les sommets sont des nœuds d’un quadrillage. On associe à un tel polygone ![]() le nombre
le nombre ![]() de points du quadrillage que ce polygone contient sans compter ceux du bord. Par exemple, pour le pentagone
de points du quadrillage que ce polygone contient sans compter ceux du bord. Par exemple, pour le pentagone ![]() de la figure 3,
de la figure 3, ![]() qui est le nombre de points rouges est égal à
qui est le nombre de points rouges est égal à ![]() (rappelons qu’il est relié à l’aire du pentagone par la formule de Pick).
(rappelons qu’il est relié à l’aire du pentagone par la formule de Pick).

Figure 2 : Construction de l’octogone intérieur

Figure 3 : Calcul de S(P)
Supposons maintenant que l’on soit capable de construire un octogone régulier dont les sommets soient des nœuds du quadrillage : ![]() . Par la construction décrite précédemment, on peut lui associer un autre octogone régulier
. Par la construction décrite précédemment, on peut lui associer un autre octogone régulier ![]() dont les sommets sont aussi sur le quadrillage car cette propriété est préservée par rotation d’angle
dont les sommets sont aussi sur le quadrillage car cette propriété est préservée par rotation d’angle ![]() et de centre un point du quadrillage. De plus, l’entier
et de centre un point du quadrillage. De plus, l’entier ![]() sera strictement inférieur à l’entier
sera strictement inférieur à l’entier ![]() . En itérant le processus, on arrive donc nécessairement à une contradiction.
. En itérant le processus, on arrive donc nécessairement à une contradiction.
Nous avons prouvé l’impossibilité en faisant un raisonnement bien connu en arithmétique depuis l’époque de Fermat : un raisonnement par descente infinie. Sur quoi repose ce raisonnement ? Sur l’impossibilité de construire une suite infinie décroissante stricte d’entiers. Cette impossibilité repose sur une propriété de l’ordre sur les entiers : celle d’être un bon ordre, c’est-à-dire un ordre tel que toute partie non vide possède un plus petit élément. En effet, supposons que l’on puisse construire une suite infinie décroissante stricte d’entiers ![]() . Notons
. Notons ![]() l’ensemble de ses termes :
l’ensemble de ses termes : ![]() . S a un plus petit élément, notons le
. S a un plus petit élément, notons le ![]() . C’est un terme de la suite, donc il existe un
. C’est un terme de la suite, donc il existe un ![]() tel que
tel que ![]() . Mais alors
. Mais alors ![]() et appartient à
et appartient à ![]() , ce qui contredit la définition de
, ce qui contredit la définition de ![]() .
.
Principe de récurrence et bon ordre sur les entiers
Le principe de récurrence, généralement introduit au lycée, découle en fait de la propriété de bon ordre des entiers. Dans l’axiomatique de l’arithmétique proposée par Peano (1908), c’est le troisième axiome et il est énoncé sous la forme suivante :
« Si ![]() est un ensemble qui contient
est un ensemble qui contient ![]() et si lorsque
et si lorsque ![]() appartient à
appartient à ![]() , le successeur de
, le successeur de ![]() appartient à
appartient à ![]() , alors tous les nombres appartiennent à
, alors tous les nombres appartiennent à ![]() ».
».
On l’énonce plus usuellement dans l’enseignement sous la forme suivante : si une propriété ![]() portant sur des entiers est satisfaite par
portant sur des entiers est satisfaite par ![]() et si, dès qu’elle satisfaite par un entier
et si, dès qu’elle satisfaite par un entier ![]() , elle l’est par son successeur
, elle l’est par son successeur ![]() , alors elle est satisfaite par tous les entiers.
, alors elle est satisfaite par tous les entiers.
Si l’on admet que l’ordre sur les entiers est un bon ordre, alors le principe de récurrence en découle directement. En effet, supposons que la propriété ![]() ne soit pas satisfaite par tous les entiers, et soit
ne soit pas satisfaite par tous les entiers, et soit ![]() l’ensemble des entiers qui ne la satisfont pas.
l’ensemble des entiers qui ne la satisfont pas. ![]() est non vide, il a donc un plus petit élément
est non vide, il a donc un plus petit élément ![]() et
et ![]() est non nul puisque
est non nul puisque ![]() satisfait
satisfait ![]() . Il a donc un prédécesseur
. Il a donc un prédécesseur ![]() qui n’est pas dans
qui n’est pas dans ![]() . Mais alors
. Mais alors ![]() satisfait
satisfait ![]() et donc également
et donc également ![]() , ce qui contredit la définition de
, ce qui contredit la définition de ![]() .
.
Le principe de récurrence peut aussi être utilisé pour définir des fonctions. C’est ce que l’on fait par exemple quand on définit des suites par récurrence, en se donnant une relation ![]() où
où ![]() est une fonction définie sur
est une fonction définie sur ![]() , et un premier terme
, et un premier terme ![]() . C’est ce que l’on appelle aussi une définition par induction.
. C’est ce que l’on appelle aussi une définition par induction.
Récurrence et induction : une première généralisation
Plus généralement, on peut raisonner par induction sur tout ensemble qui est muni d’un bon ordre. Considérons par exemple l’ensemble ![]() muni de l’ordre lexicographique
muni de l’ordre lexicographique ![]() si
si ![]() ou
ou ![]() et
et ![]() . Cet ordre est un bon ordre. En effet soit
. Cet ordre est un bon ordre. En effet soit ![]() un sous ensemble non vide de
un sous ensemble non vide de ![]() , nous pouvons distinguer deux cas :
, nous pouvons distinguer deux cas :
- soit tous les éléments de
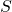 sont de la forme
sont de la forme 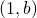 . Alors
. Alors 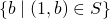 est un sous-ensemble non vide de
est un sous-ensemble non vide de 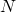 et il a un plus petit élément
et il a un plus petit élément 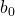 . Alors
. Alors 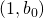 est le plus petit élément de
est le plus petit élément de 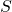 ;
; - soit, il existe un élément de
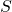 de la forme
de la forme 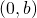 . Alors, montrer que
. Alors, montrer que 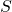 a un plus petit élément revient à montrer que
a un plus petit élément revient à montrer que 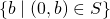 a un plus petit élément, ce qui est nécessairement le cas.
a un plus petit élément, ce qui est nécessairement le cas.
De la même façon, l’ordre lexicographique sur ![]() et plus généralement sur
et plus généralement sur ![]() est un bon ordre. Nous laissons au lecteur le soin d’adapter à ces cas la démonstration ci-dessus. Dans ces ensembles donc, il ne peut exister de suite infinie décroissante stricte et ce, même si pour tout élément de la forme
est un bon ordre. Nous laissons au lecteur le soin d’adapter à ces cas la démonstration ci-dessus. Dans ces ensembles donc, il ne peut exister de suite infinie décroissante stricte et ce, même si pour tout élément de la forme ![]() avec
avec ![]() il existe une infinité d’éléments qui lui sont inférieurs, tous ceux de la forme
il existe une infinité d’éléments qui lui sont inférieurs, tous ceux de la forme ![]() avec
avec ![]() .
.
Dans ![]() donc, le raisonnement par descente infinie que nous avons utilisé dans le premier exemple s’applique. Et dans
donc, le raisonnement par descente infinie que nous avons utilisé dans le premier exemple s’applique. Et dans ![]() , on peut également définir des fonctions par induction. C’est le cas par exemple pour la célèbre fonction de
, on peut également définir des fonctions par induction. C’est le cas par exemple pour la célèbre fonction de ![]() dans
dans ![]() introduite par Ackermann en 1932 sur laquelle nous reviendrons dans la suite de cette vignette.
introduite par Ackermann en 1932 sur laquelle nous reviendrons dans la suite de cette vignette.
Induction et ordinaux
Dans la théorie des ensembles, cette notion de bon ordre, essentielle au raisonnement mathématique, s’exprime à travers la notion d’ordinal et l’on ne s’y arrête pas à des bons ordres comme ceux mentionnés ci-dessus. Les ordinaux et donc les entiers eux-mêmes qui sont les ordinaux finis y sont définis comme des ensembles bien ordonnés par la relation d’appartenance et transitifs (un ensemble ![]() est transitif si pour tout élément
est transitif si pour tout élément ![]() d’un élément
d’un élément ![]() de
de ![]() est aussi un élément de
est aussi un élément de ![]() ), mais nous nous contenterons ici d’une vision plus intuitive de ce que sont les ordinaux transfinis introduits par Cantor à la fin du 19e siècle. Le premier ordinal infini est noté
), mais nous nous contenterons ici d’une vision plus intuitive de ce que sont les ordinaux transfinis introduits par Cantor à la fin du 19e siècle. Le premier ordinal infini est noté ![]() et il est la réunion de tous les ordinaux finis. Il représente l’ordre sur les entiers. Il a un successeur
et il est la réunion de tous les ordinaux finis. Il représente l’ordre sur les entiers. Il a un successeur ![]() qui a lui-même pour successeur
qui a lui-même pour successeur ![]() , et ainsi de suite… Le plus petit ordinal plus grand que tous les
, et ainsi de suite… Le plus petit ordinal plus grand que tous les ![]() est
est ![]() noté aussi
noté aussi ![]() . Le plus petit ordinal plus grand que tous les
. Le plus petit ordinal plus grand que tous les ![]() est
est ![]() et l’on continue ainsi.
et l’on continue ainsi.
![]()
Il y a en fait deux types d’ordinaux, ceux qui sont successeurs d’un ordinal donné comme ![]() ,
, ![]() , pour
, pour ![]() non nul, et ceux qui n’ont pas de prédécesseur mais sont la réunion de tous les ordinaux inférieurs, comme
non nul, et ceux qui n’ont pas de prédécesseur mais sont la réunion de tous les ordinaux inférieurs, comme ![]() ,
, ![]() ,
, ![]() dans la liste ci-dessus. On remarquera que l’ordre lexicographique que nous avons mis sur
dans la liste ci-dessus. On remarquera que l’ordre lexicographique que nous avons mis sur ![]() munit cet ensemble d’un ordre qui n’est autre que celui de l’ordinal
munit cet ensemble d’un ordre qui n’est autre que celui de l’ordinal ![]() . La généralisation de cet ordre à l’ordre lexicographique sur
. La généralisation de cet ordre à l’ordre lexicographique sur ![]() correspond à
correspond à ![]() , … Mais il y a bien d’autres ordinaux que ceux que nous avons évoqués ici qui en fait sont tous dénombrables. En théorie des ensembles on peut démontrer, en utilisant l’axiome du choix, que tout ensemble peut être bien ordonné.
, … Mais il y a bien d’autres ordinaux que ceux que nous avons évoqués ici qui en fait sont tous dénombrables. En théorie des ensembles on peut démontrer, en utilisant l’axiome du choix, que tout ensemble peut être bien ordonné.
On peut définir des fonctions par induction sur les ordinaux. Pour définir une fonction par induction sur un ordinal ![]() , il faut donner sa valeur en
, il faut donner sa valeur en ![]() et un procédé qui permet d’obtenir la valeur de
et un procédé qui permet d’obtenir la valeur de ![]() à partir des valeurs de la fonction pour les ordinaux précédents. Notons qu’il est souvent commode de distinguer deux cas pour définir
à partir des valeurs de la fonction pour les ordinaux précédents. Notons qu’il est souvent commode de distinguer deux cas pour définir ![]() , selon que
, selon que ![]() est limite ou successeur. Sur les ordinaux, on peut raisonner par descente infinie et la vignette Goodstein donne un exemple de tel raisonnement.
est limite ou successeur. Sur les ordinaux, on peut raisonner par descente infinie et la vignette Goodstein donne un exemple de tel raisonnement.
Retour sur la fonction d’Ackermann et méthode de diagonalisation
Un exemple de fonction définie par induction est la fonction d’Ackermann évoquée plus haut. Notée ![]() , elle est définie comme suit :
, elle est définie comme suit :
- Pour tout entier
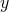 ,
, 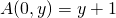
- Pour tout entier
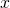 ,
, 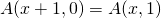
- Pour tout couple d’entiers
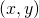 ,
, 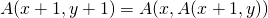 .
.
Sa valeur en un point ![]() est donc donnée explicitement si
est donc donnée explicitement si ![]() est nul. Lorsque
est nul. Lorsque ![]() est non nul, le calcul de
est non nul, le calcul de ![]() utilise des valeurs de la fonction elle-même mais en des points
utilise des valeurs de la fonction elle-même mais en des points ![]() tels que
tels que ![]() pour l’ordre lexicographique. Ce calcul fait donc intervenir une suite strictement décroissante de tels points et cette suite est nécessairement finie puisque l’ordre lexicographique est un bon ordre. Elle peut en revanche être très longue. Combien de termes faut-il calculer par exemple pour obtenir
pour l’ordre lexicographique. Ce calcul fait donc intervenir une suite strictement décroissante de tels points et cette suite est nécessairement finie puisque l’ordre lexicographique est un bon ordre. Elle peut en revanche être très longue. Combien de termes faut-il calculer par exemple pour obtenir ![]() ?
?
Commençons avec un exemple plus simple. Calculons ![]() en remplissant progressivement le tableau suivant :
en remplissant progressivement le tableau suivant :
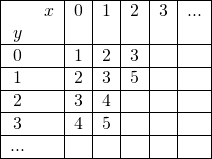
La première condition ![]() permet de remplir la première colonne. Ensuite, nous avons successivement :
permet de remplir la première colonne. Ensuite, nous avons successivement :
![]() ;
; ![]() ;
; ![]() , et plus généralement on a :
, et plus généralement on a :
![]()
On peut alors calculer :
![]() ;
; ![]() et finalement
et finalement ![]() .
.
On voit donc que, pour calculer ![]() , on utilise toutes les valeurs de la fonction pour les couples de la première colonne jusqu’à
, on utilise toutes les valeurs de la fonction pour les couples de la première colonne jusqu’à ![]() , de la deuxième jusqu’à
, de la deuxième jusqu’à ![]() , et de la troisième jusqu’à
, et de la troisième jusqu’à ![]() , soit
, soit ![]() valeurs.
valeurs.
Que se passe-t-il quand on veut calculer ![]() et quelle est la valeur finalement obtenue pour
et quelle est la valeur finalement obtenue pour ![]() ? Nous laissons au lecteur le soin de répondre à cette question.
? Nous laissons au lecteur le soin de répondre à cette question.
En fixant une des deux variables dans la fonction d’Ackermann, on obtient ce qu’il est convenu d’appeler les fonctions arithmétiques. Ainsi, si on note ![]() , la fonction obtenue en fixant la première variable à la valeur
, la fonction obtenue en fixant la première variable à la valeur ![]() , nous avons vu que
, nous avons vu que ![]() , donc
, donc ![]() est la fonction successeur et
est la fonction successeur et ![]() . On peut montrer que
. On peut montrer que ![]() et
et ![]() . Ensuite, très vite, les expressions se compliquent, faisant intervenir des itérations de puissances et les valeurs de
. Ensuite, très vite, les expressions se compliquent, faisant intervenir des itérations de puissances et les valeurs de ![]() deviennent en fait terriblement grandes en quelques étapes seulement. Par exemple,
deviennent en fait terriblement grandes en quelques étapes seulement. Par exemple, ![]() et
et ![]() est un nombre de
est un nombre de ![]() chiffres.
chiffres.
En fait, on peut démontrer que la fonction ![]() définie par
définie par ![]() est telle que, pour toute fonction récursive primitive, c’est-à-dire toute fonction qui peut être construire à partir de la fonction successeur et des fonctions projections de
est telle que, pour toute fonction récursive primitive, c’est-à-dire toute fonction qui peut être construire à partir de la fonction successeur et des fonctions projections de ![]() dans
dans ![]() par composition et récurrence, il existe un entier
par composition et récurrence, il existe un entier ![]() telle que
telle que ![]() pour tous les
pour tous les ![]() supérieurs à
supérieurs à ![]() . C’est ainsi que l’on prouve qu’il existe des fonctions calculables qui ne sont pas récursives primitives. La fonction d’Ackermann en est justement un exemple. Mais les fonctions usuelles sur les entiers, toutes celles que l’on manipule dans l’enseignement secondaire, sont bien, elles, des fonctions récursives primitives. Les fonctions qui à deux nombres entiers
. C’est ainsi que l’on prouve qu’il existe des fonctions calculables qui ne sont pas récursives primitives. La fonction d’Ackermann en est justement un exemple. Mais les fonctions usuelles sur les entiers, toutes celles que l’on manipule dans l’enseignement secondaire, sont bien, elles, des fonctions récursives primitives. Les fonctions qui à deux nombres entiers ![]() et
et ![]() associent leur somme et leur produit sont bien récursives primitives. On peut en effet les définir par récurrence en posant : pour tout
associent leur somme et leur produit sont bien récursives primitives. On peut en effet les définir par récurrence en posant : pour tout ![]() ,
, ![]() et
et ![]() et pour tout
et pour tout ![]() ,
, ![]() et
et ![]() . On laisse le lecteur en déduire que la fonction qui, au couple d’entiers
. On laisse le lecteur en déduire que la fonction qui, au couple d’entiers ![]() associe
associe ![]() est elle aussi récursive primitive, ainsi que toute itération finie de telles exponentielles. Plus généralement, toute fonction qui peut se définir à partir de fonctions récursives primitives par un algorithme faisant intervenir une boucle de la forme « Pour
est elle aussi récursive primitive, ainsi que toute itération finie de telles exponentielles. Plus généralement, toute fonction qui peut se définir à partir de fonctions récursives primitives par un algorithme faisant intervenir une boucle de la forme « Pour ![]() allant de
allant de ![]() à
à ![]() » est récursive primitive.
» est récursive primitive.
La preuve fait appel à un argument de diagonalisation. C’est Georg Cantor qui, en 1874, inventa ce type d’argument pour démontrer que l’ensemble des nombres réels est non dénombrable, c’est-à-dire ne peut pas être mis en bijection avec l’ensemble des entiers. En 1891, il utilisa aussi cette méthode pour montrer que l’ensemble des parties d’un ensemble ![]() a toujours un cardinal strictement supérieur à celui de
a toujours un cardinal strictement supérieur à celui de ![]() . L’invention de cette méthode diagonale a été une étape importante pour le développement de la logique mathématique. Elle est notamment à la base de la preuve de nombreux résultats dont le théorème d’incomplétude de Gödel, et de nombreux théorèmes de théorie de la calculabilité. Le paradoxe de Russell est également basé sur cette idée. On peut, dans l’enseignement secondaire, faire sentir la puissance de ce mode de raisonnement, en l’utilisant pour démontrer que l’intervalle
. L’invention de cette méthode diagonale a été une étape importante pour le développement de la logique mathématique. Elle est notamment à la base de la preuve de nombreux résultats dont le théorème d’incomplétude de Gödel, et de nombreux théorèmes de théorie de la calculabilité. Le paradoxe de Russell est également basé sur cette idée. On peut, dans l’enseignement secondaire, faire sentir la puissance de ce mode de raisonnement, en l’utilisant pour démontrer que l’intervalle ![]() n’est pas dénombrable, en s’appuyant sur le fait que tout nombre réel possède un développement décimal unique (à condition de ne pas considérer les développements impropres qui se terminent par une infinité de
n’est pas dénombrable, en s’appuyant sur le fait que tout nombre réel possède un développement décimal unique (à condition de ne pas considérer les développements impropres qui se terminent par une infinité de ![]() ). Supposons que l’intervalle
). Supposons que l’intervalle ![]() soit un ensemble dénombrable et considérons un rangement de ces réels en une suite
soit un ensemble dénombrable et considérons un rangement de ces réels en une suite ![]() . Le développement décimal illimité propre associé au réel
. Le développement décimal illimité propre associé au réel ![]() est de la forme :
est de la forme : ![]() ,
,![]() , et se termine par une infinité de
, et se termine par une infinité de ![]() si
si ![]() est un nombre décimal. Considérons alors le réel
est un nombre décimal. Considérons alors le réel ![]() dont le développement décimal illimité est
dont le développement décimal illimité est ![]() avec
avec ![]() si
si ![]() et
et ![]() si
si ![]() . Il est alors clair que
. Il est alors clair que ![]() est le développement décimal illimité propre d’un réel
est le développement décimal illimité propre d’un réel ![]() de l’intervalle
de l’intervalle ![]() et que le réel
et que le réel ![]() n’est égal à aucun des réels de la suite
n’est égal à aucun des réels de la suite ![]() . L’intervalle
. L’intervalle ![]() n’est donc pas dénombrable et a fortiori l’ensemble des nombres réels.
n’est donc pas dénombrable et a fortiori l’ensemble des nombres réels.
Morale
Le raisonnement par récurrence ou induction est présent dans les mathématiques dès l’antiquité. Dans les Eléments d’Euclide, il sert par exemple à prouver l’existence d’une infinité de nombres premiers. Parallèlement, le raisonnement par descente infinie est lui aussi présent dans les mathématiques depuis des siècles et on attache souvent son nom à celui de Fermat qui en a fait un usage répété dans ses travaux de théorie des nombres. Montrer l’équivalence de ces deux modes de raisonnement est en revanche une conquête plus récente, liée au développement de la logique mathématique. L’outil essentiel pour cela est la notion de bon ordre. Cette notion dans laquelle Georg Cantor voyait « un outil fondamental de la pensée » permet non seulement de comprendre l’équivalence entre récurrence et descente infinie mais aussi de raisonner par induction sur des ensembles autres que les seuls entiers et de comprendre notamment comment fonctionnent des récurrences imbriquées (doubles, triples) comme celles à l’œuvre dans la définition de la fonction d’Ackermann.
L’exemple par lequel nous avons débuté cette vignette a été choisi pour montrer que le raisonnement par induction est un outil général en mathématiques, et non pas un outil réservé à la seule théorie des nombres. Il joue un rôle déterminant notamment dans les mathématiques discrètes.
Au-delà de la seule induction, cette vignette a été l’occasion d’évoquer d’autres questions, non indépendantes des premières, et très importantes comme celle de la calculabilité. La mathématisation de la notion intuitive de calculabilité qui a nécessité le codage de différents types d’objets discrets, et l’utilisation des méthodes de diagonalisation a permis d’obtenir des résultats profonds dans différents domaines. Elle est aussi essentielle aux connexions entre mathématiques et informatique.
Références
[1] Calude C., Marcus S., Tevy, I (1979). The first example of a recursive function which is not primitive recursive, Historia Math., vol. 6, n. 4, 380–84.
[2] Cori, R., Lascar D. (). Logique mathématique, tome 2 : Fonctions récursives, théorème de Gödel, théorie des ensembles, théorie des modèles. Paris : Editions Dunod.
[3] Payan C. (1992). Une belle histoire de polygones et de pixels. MATh.en.JEANS” au Palais de la Découverte, pp. 99-106. mathenjeans.free.fr/amej/edition/actes/actespdf/92099106.pdf
