A autora original é Christiane Rousseau. A tradução para o Português é de Humberto José Bortolossi.
A autora original é Christiane Rousseau. A tradução para o Português é de Humberto José Bortolossi.
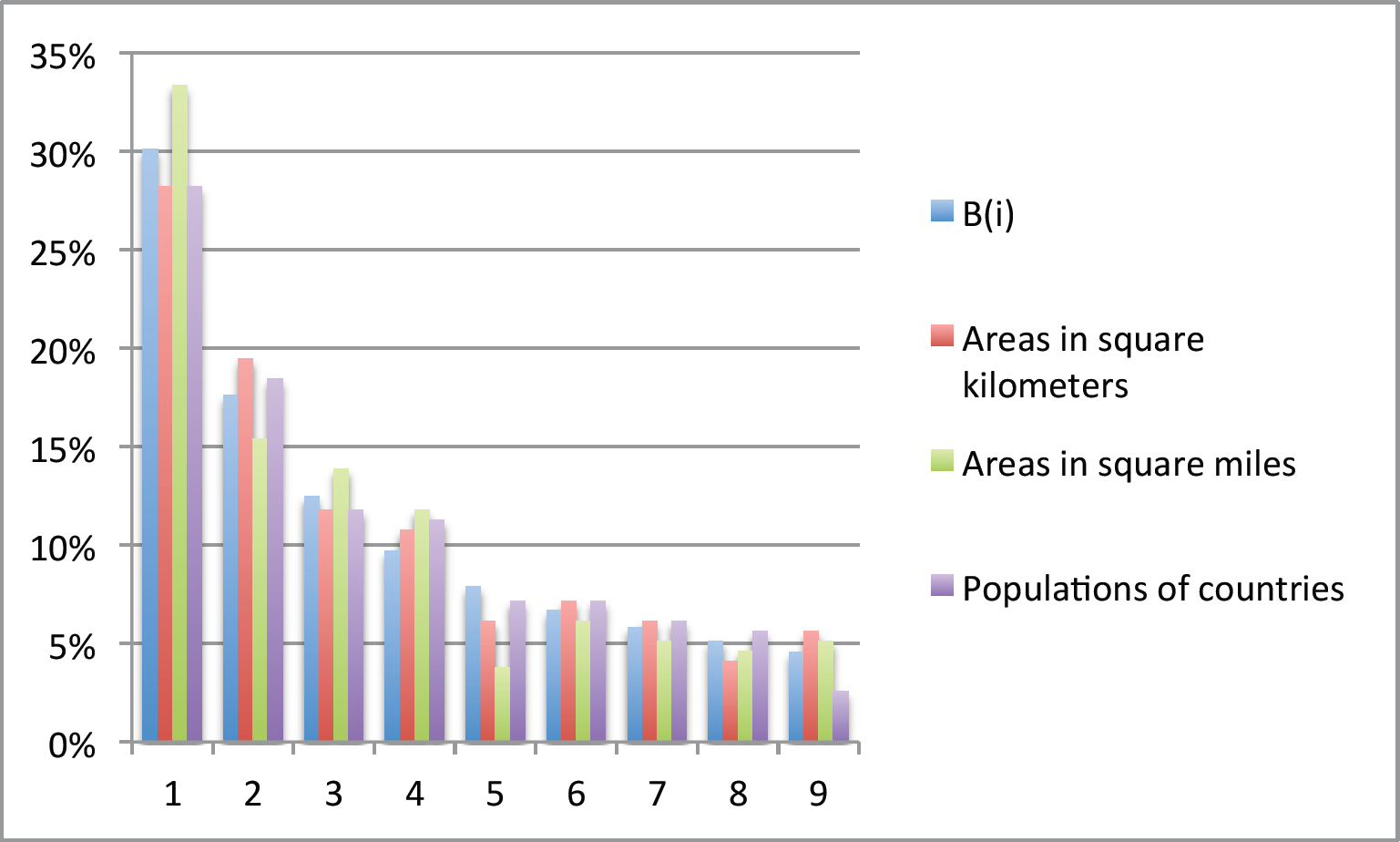
É muito arriscado ficar alterando números demais em relatórios financeiros se você não conhece matemática. De fato, a maioria dos números que aparecem em declarações financeiras seguem uma regra matemática estranha, denominada de Lei de Benford ou Lei do Primeiro Dígito Significativo. Se alguém se esquecer de seguir essa regra, então os números alterados não irão passar em alguns testes estatísticos e provavelmente eles cairão em uma malha fina. A Lei de Benford afirma que se você coletar números de forma aleatória e calcular as frequências de seus primeiros dígitos significativos, então os números com primeiro digito significativo igual a ![]() aparecerão cerca de
aparecerão cerca de ![]() % das vezes, enquanto que os números com primeiro dígito significativo igual a
% das vezes, enquanto que os números com primeiro dígito significativo igual a ![]() aparecerão somente
aparecerão somente ![]() % das vezes. Esta regra é observada em muitos outros conjuntos de números, como potências de
% das vezes. Esta regra é observada em muitos outros conjuntos de números, como potências de ![]() e os números de Fibonacci.
e os números de Fibonacci.
Receive notice of every new vignette.
Search
Meta