La revancha de los infinitésimos

Autor original: Michèle Artigue.
Traducción: Tomás Recio, Universidad de Cantabria.

Los infinitésimos han jugado un papel clave en la emergencia y desarrollo del cálculo diferencial e integral. La evidente productividad de este cálculo no ha impedido que se produzcan debates recurrentes y, a veces, feroces sobre la naturaleza de estos objetos (los infinitésimos) y sobre la legitimidad de su uso. A finales del siglo XIX, cuando la construcción de los números reales a partir de los números enteros y la definición moderna del limite proporcionaron fundamentos sólidos al cálculo diferencial e integral, los infinitésimos, y la metafísica que los rodeaba, fueron rechazados y su uso se volvió sinónimo de prácticas poco rigorosas, ya superadas. Sin embargo el lenguaje de los infinitésimos siguió siendo utilizado, por ejemplo, en la física; e incluso en las matemáticas nunca desapareció por completo del discurso informal, del pensamiento heurístico de muchos investigadores.

¿Es, pues, este lenguaje realmente incompatible con el rigor matemático? ¿Qué es lo que ofrece, interesante o específico, que explique su permanencia? El Análisis no estándar, que se desarrolló en el siglo XX, ha permitido responder a estas preguntas y, a los infinitésimos, tomarse su revancha.

Del cálculo infinitesimal al Análisis no estándar

En el prefacio del primer tratado de análisis infinitesimal, publicado en 1696, su autor, el Marqués de l’Hôpital, evidencia la potencia y simplicidad del nuevo cálculo facilitado por los infinitésimos: $^i$ :

Figura 1: Cubierta y extracto del prefacio del tratado del Marques de l’Hôpital

Sin embargo, muy pronto, se desarrollaron diversos debates en torno a estos objetos y a su uso. En un famoso ensayo publicado en 1734, The Analyst, George Berkeley hace una crítica feroz del uso de estos infinitésimos –o incrementos evanescentes– en el cálculo diferencial; y Jean Le Rond d’Alembert, en l’Encyclopédie Méthodique, publicada en 1751, propone ya liberarse de ellos, apoyándose en la idea de límite. En los umbrales del siglo XX, con el desarrollo del análisis moderno, esto parece cosa hecha. Sin embargo, medio siglo después, el trabajo del lógico Abraham Robinson va a rehabilitar los infinitésimos y las prácticas asociadas.

En efecto: Abraham Robinson muestra que el lenguaje de los infinitésimos es totalmente compatible con el rigor matemático. Ya en 1934 el lógico Thoralf Skolem había mostrado que el conjunto obtenido sumando unidades sucesivas a partir de 0 no podía ser el único modelo de la axiomática de Peano, sino que existían modelos diferentes –llamados no estándar– de esta aritmética. En 1961 Abraham Robinson muestra, a través de una construcción a base de ultra-productos, la existencia de un modelo no estándar de los números reales conteniendo números «infinitamente grandes» y « infinitamente pequeños ». Fue el nacimiento del Análisis No Estándar (ANE). Posteriormente, Edward Nelson, en 1977, encuentra una manera de axiomatizar el ANE. Para ello añade al lenguaje de la teoría de conjuntos un símbolo de predicado con una variable, $st(x)$ , expresando que un objeto $x$ es estándar, y a la axiomática ZFC $^{ii}$ de esta teoría, añade tres axiomas: los axiomas de idealización, de estandarización y de transferencia $^{iii}$ , lo que hace el ANE más fácilmente manipulable. En esta viñeta nos apoyamos en esta axiomatización denominada IST (Internal Set Theory).

Estos tres axiomas tienen consecuencias importantes. Se deduce, por ejemplo, del axioma de transferencia que dos conjuntos estándar E1 y E2 son iguales si y solo si tienen los mismos elementos estándar $^{iv}$ . Se deduce de este mismo axioma que si existe un $x$ que satisface una propiedad clásica $P$ , es decir una propiedad que se puede expresar sin utilizar el predicado st, existe necesariamente un $x$ estándar que la satisface. Por tanto, los objetos que se pueden definir de manera única por una formula clásica son, necesariamente, objetos estándar. Los números y los objetos usuales que encontramos en matemática: los números $\pi$ , $e$ , las funciones trigonométricas y exponenciales, etc. son objetos estándar, así como el conjunto vacío, el conjunto $\mathbb{N}$ de los enteros naturales y el conjunto $\mathbb{R}$ de los números reales.

Sin embargo, ser un conjunto estándar no implica tener sólo elementos estándar. De hecho, también se deduce del axioma de idealización que existe un entero mayor que todos los enteros estándar, y por eso necesariamente no estándar; y que, más generalmente, cualquier conjunto infinito contiene necesariamente al menos un elemento no estándar $^v$ . $\mathbb{R}$ y $\mathbb{N}$ son, pues, conjuntos estándar que contienen elementos no estándar. ¿Cómo representarlos?

En $\mathbb{N}$ , todos los enteros estándar preceden a los enteros no estándar. En $\mathbb{R}$ la situación es algo más complicada. Se pueden distinguir, de acuerdo a su tamaño, tres tipos de números reales:

los reales muy pequeños o infinitesimales (positivos y negativos), aquellos cuyo valor absoluto es menor que cualquier real estándar positivo,
los reales muy grandes o infinitamente grandes (positivos y negativos), aquellos cuyo valor absoluto es mayor que cualquier real estándar positivo,
y, entre los dos, los reales a escala humana –podríamos decir–, que a menudo se llaman apreciables.

Si un real es un infinitésimo o es apreciable, se dice que es limitado. Si un real es infinitamente grande su inverso es un infinitésimo y ambos son necesariamente no estándar. Por el contrario, los reales apreciables pueden ser estándar o no. Consideremos, por ejemplo, el número real $1$ al que se le añade un real $\alpha$ infinitesimal y no nulo, obteniendo el real $1+\alpha$ , que es también apreciable, infinitamente próximo a $1$ y no estándar. Alrededor de cada real estándar existe una nube de reales no estándar infinitamente cercanos. Para apreciar mejor esto introduzcamos una nueva relación: diremos que $x$ es infinitamente cercano a $y$ si $x-y$ es un infinitésimo, lo que denotaremos por $x \simeq y$ . Llamaremos halo de un real a la colección de los reales que son infinitamente cercanos a un real dado. Así los infinitésimos son el halo de $0$ ; y cualquier real apreciable x pertenece al halo de un único real estándar, que se denomina su parte estándar. Uno puede imaginar la recta real como se muestra en la figura 2, con una frontera no claramente marcada entre reales apreciables y reales infinitamente grandes, porque la colección de los apreciables positivos no tiene un máximo, ni tampoco la colección de los infinitamente grandes positivos posee un mínimo.

Figura 2: Representación de la recta real no estándar

Pueden darse reglas de cálculo, extendiendo las de la aritmética clásica, teniendo en cuenta las diferencias de magnitud de los números reales en la recta no estándar. Así, si denotamos por $ip$ a los infinitésimos, por $app$ a los apreciables y por $ig$ a los infinitamente grandes, tenemos por ejemplo: $ip * app = ip$ , $ip + app = app$ , $ip * ip = ip$ e $ip + ig = ig$ . Invitamos al lector a completar, cuando sea posible, las dos tablas siguientes.

Rendered by QuickLaTeX.com

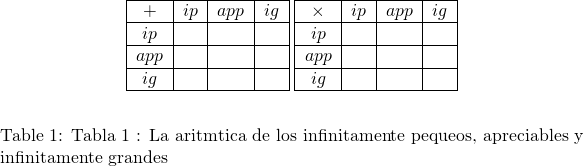
El conjunto de los números reales siempre satisface el principio de Arquímedes: si $a$ y $b$ son reales positivos tales que $0<a<b$ , existe un entero $n$ tal que $na>b$ ; pero si $a$ es infinitamente pequeño y si $b$ no es, $n$ es necesariamente infinitamente grande.

El ANE y las nociones básicas del análisis

En el marco del ANE, los conceptos básicos del análisis matemático: límites, continuidad, derivabilidad, integrabilidad, se formalizan de manera muy sencilla para los objetos estándar, como se muestra en la siguiente tablai $^{vi}$ :

Rendered by QuickLaTeX.com

Estas formalizaciones simples, sin alternancias de cuantificadores, y las ideas subyacentes, permiten demostraciones simplificadas de muchos teoremas clásicos. Así, el cuadro de abajo propone una demostración simplificada del teorema del valor medio.

Teorema del valor medio $^{vii}$ : Sea $I$ un intervalo de $\mathbb{R}$ , $f$ una función real continua sobre $I$ , $a$ y $b$ dos reales con $a<b$ . Entonces, para todo real $y$ entre $f(a)$ y $f(b)$ , existe un real $c$ de $[a, b]$ tal que $f(c) = y$ . Demostración: Sin pérdida de generalidad se puede suponer en la prueba que $y = 0$ y $f(a)<0<f(b)$ . Sea $\omega$ un real infinitamente grande y consideremos la subdivisión de $[a, b]$ de amplitud $(b-a)/\omega$ (es decir, $x_0=a$ , … , $x_n=a+n(b-a)/\omega$ ,… , $x_{\omega}=b$ ). Sea $m$ el primer índice tal que $f(x_m)>0$ . Por hipótesis $m \neq 0$ y $x_m$ es un real limitado, porque está situado entre $a$ y $b$ . Tomemos como $c$ la parte estándar de $x_m$ . Entonces $f(x_{m-1}) \leq 0$ y $f(xm)>0$ pero $x_{m-1} \simeq x_m$ ya que el paso de subdivisión es infinitesimal. Además $x_m \simeq c$ . Al ser $f$ continua en $c$ , $f(c) \simeq f(x_{m-1}) \simeq f(x_m)$ y, como $f(c)$ es estándar, $f(c)=0$ .

El ANE también permite justificar las técnicas infinitesimales siempre utilizadas fuera de la comunidad matemática para calcular áreas, volúmenes, momentos de inercia, centros de gravedad… o para modelar situaciones utilizando ecuaciones diferenciales. El siguiente ejemplo es una ilustración sencilla.

Cálculo del volumen de la esfera:

Sea $S$ una esfera de radio $R$ . Cortemos la esfera en rodajas de espesor infinitesimal $dz$ . El volumen $dV$ de la rodaja a la altura $z$ es, aproximadamente, el del cilindro de radio $\sqrt{R^2 - z^2}$ y de altura $dz$ .
$dV = \pi (R^2 - z^2)dz$
de donde, sumando, se obtiene:
$V=\int_{-R}^{R} \pi(R^2 - z^2) dz$
$V=\left[ \pi (R^2 z - z^3 /3) \right]_{-R}^{R}$
y finalmente $V=\frac{4 \pi R^3}{3}$ .

Figura 3: El volumen de la esfera

La suma de los volúmenes de los cilindros infinitesimales es la suma de Cauchy, asociada a la subdivisión, de anchura infinitesimal $dz$ , del intervalo $[-R, R]$ , para la función área $S(z)=\pi (R^2-z^2)$ . La parte estándar de esta suma es, pues, igual, por definición no estándar de la integral de una función continua, a la integral $\int_{-R}^R S(z) dz$ .
Sin embargo, si esta integral da el volumen de la esfera es porque la aproximación propuesta para $dV$ es equivalente al volumen de la rodaja, y no sólo un volumen infinitamente cercano. Este no sería el caso si se utilizara esta misma técnica de aproximación para calcular el área de la esfera mediante cilindros infinitesimales, por ejemplo.

La necesidad de cierta vigilancia
Sin embargo, manipular objetos que no son estándar, requiere cierta precaución. Por ejemplo, si ampliamos la definición anterior de continuidad a cualquier función y a cualquier número real, estándar o no, uno obtiene cierta noción de $S$ -continuidad en un punto, que no necesariamente se corresponde con nuestra visión de las funciones continuas. Por ejemplo, la función escalonada que vale $0$ para los reales estrictamente negativos y $\alpha$ para los reales positivos o nulos, donde $\alpha$ es infinitamente pequeño no nulo, es $S$ -continua en $0$ , ya que la imagen de cualquier infinitesimal positivo es el infinitesimal $\alpha$ . Por el contrario, la función cuadrado no es $S$ -continua en $\omega$ , si $\omega$ es infinitamente grande, ya que $(\omega+1/\omega)^2=\omega^2+1/\omega^2+2$ no es infinitamente cercano a $\omega^2$ . De hecho, para funciones estándar, la $S$ -continuidad en cualquier punto de $\mathbb{R}$ equivale a la continuidad uniforme sobre $\mathbb{R}$ , y el cálculo que acabamos de hacer para la función cuadrado muestra, muy simplemente, que esta función no es uniformemente continua sobre $\mathbb{R}$ .

El uso del ANE también exige atención respecto al empleo del principio de inducción. En su forma usual se puede aplicar –como consecuencia del axioma de transferencia– a propiedades clásicas; pero no puede generalizarse más allá. Por ejemplo, considérese el siguiente argumento, que a menudo se presenta como paradójico:

Sea $P$ la propiedad “Ser estándar”. $P(0)$ es verdadera y, para cualquier número entero $n$ , si $P(n)$ es verdadera entonces $P(n +1)$ también es verdadera. Así que, para todo $n$ , $P(n)$ es verdadera y todos los enteros son estándar.

El principio de inducción es aplicado aquí a un enunciado no clásico, porque ha sido formulado con el predicado $st$ . El razonamiento no es paradójico. Simplemente no es válido. De hecho, se puede mostrar que para una propiedad $P$ cualquiera sólo es valido el principio reducido de recurrencia siguiente: Si $P(0)$ es verdadera y si, para cualquier entero $n$ , $P(n)$ implica $P(n +1)$ , entonces $P$ es cierta para todo entero estándar.

Las potencialidades del ANE : Una cuestión que aún se debate

Como vemos, el ANE rehabilita a los infinitésimos, a los métodos de cálculo y a las intuiciones asociadas a ellos, pero a cambio de cierto trabajo y precauciones. Entonces, ¿qué se gana realmente con el ANE? La cuestión sigue siendo objeto de debate, como lo muestra, por ejemplo, el blog del matemático Terence Tao al que tuvimos acceso preparando esta viñeta. El ANE se ha utilizado en diversas áreas de las matemáticas: en particular, en topología, probabilidad y sistemas dinámicos. También ha contribuido a modelizaciones interesantes, por ejemplo, en automática, ecología y economía. En Francia, por iniciativa del matemático Georges Reeb, a finales de los años 70 se desarrolló una comunidad ANE que produjo resultados originales en muchas áreas (ver (Lutz y Goze , 1982) (Diener y Diener, 1995)). Uno de los más conocidos es el descubrimiento de trayectorias, llamadas «patos», en campos de vectores lentos-rápidos, en dos y tres dimensiones. Presentamos a continuación este ejemplo, sin entrar, sin embargo, en detalles técnicos de su tratamiento no estándar. El lector poco familiarizado con ecuaciones diferenciales puede saltar esta parte.

Las trayectorias «pato»

Consideremos la ecuación diferencial $cx''+(x^2-1)x'+x-a=0$ , con $a \geq 0$ y $c>0$ . Un estudio clásico de esta ecuación muestra que, si $a <1$ , la ecuación tiene una solución única periódica, que es un ciclo límite atractivo. Esta solución periódica desaparece para $a=1$ ; y para $a \geq 1$ existe un estado atractivo estacionario con $x=a$ . El fenómeno de las trayectorias pato se produce antes de esta bifurcación de la dinámica, conocida como bifurcación de Hopf, para valores de $c$ muy pequeños y valores de $a$ muy cerca de $1$ . Un modelo no estándar, suponiendo $c$ infinitamente pequeño, permitió identificar el fenómeno y caracterizar las condiciones de su aparición.

Para empezar, se transforma la ecuación en un sistema, y esto de dos maneras diferentes: bien poniendo $u=cx'+F(x)$ , con $F(x)=x^3/3-x$ , una transformación clásica para estudiar este tipo de ecuación llamada de Lienard, o bien clásicamente, poniendo $v=x'$ . Se obtienen así los dos sistemas siguientes, donde $\omega=1/c$ es un real infinitamente grande:

$\left\{ \begin{array}{cl} x' &= \omega (u-F(x)), \\ u' &= a-x \end{array}\right$

$\left\{ \begin{array}{cl} x' &= \omega (u-F(x)), \\ v' &= \omega(a-x-(x^2 -1)v) \end{array}\right$

En las figuras 1 y 2, copiadas de (Benoît et al., 1981), se reproducen los campos asociados en los planos $(x, u)$ y $(x, v)$ . Estos campos son lentos-rápidos. Por ejemplo, el campo del plano $(x, u)$ , o plano de Lienard, es casi horizontal fuera del halo de la cúbica $C$ , de ecuación $u=f(x)$ , cuyas partes crecientes, vista la dirección de las flechas horizontales, son atractivas; mientras que la parte decreciente es repulsiva. Las flechas dobles indican que estas partes cuasi-horizontales están recorridas con una velocidad infinitamente alta. Se muestra, mediante la combinación de técnicas de análisis clásico y de análisis no estándar, particularmente el uso de cambios de escala con ampliaciones infinitamente grandes en una dirección, en los planos $(x, u)$ y $(x, v)$ , que cuando $a < 1$ , pero no en el halo de $1$ , hay un único gran ciclo atractivo (Figura 3). En el plano $(x, u)$ , una partícula moviéndose en este ciclo, partiendo, por ejemplo, de un punto $M$ no situado en el halo de $C$ , se mueve horizontalmente a una velocidad infinitamente alta hasta llegar en el halo de $C$ y después se mueve quedando en este halo con una velocidad apreciable $x' \simeq (a-x)/(x^2-1)$ siguiendo la dirección de desplazamiento indicada por la flechas sobre $C$ , hasta llegar al halo de su mínimo local $S-$ . A continuación sale del halo para retomar un movimiento cuasi horizontal hasta entrar de nuevo en el halo de $C$ y seguirlo hasta el halo del máximo local $S+$ , antes de volver a partir de nuevo horizontalmente.

Cuando $a \simeq 1$ , la situación se complica debido a que las ramas separadas de la curva Ha, asociada a $v'= 0$ en el plano de fases $(x,v)$ , se vuelven infinitamente próximas. Se sigue que una solución que, en el plano $(x,u)$ , ha seguido sobre $C$ hasta llegar al halo de $S-$ puede, para ciertos valores de $a$ , continuar siguiendo una porción de la parte repulsiva de $C$ antes de abandonar su halo para moverse casi horizontalmente y llegar al halo de la parte atractiva de $C$ (Figura 4).

Figura 4: Morfología de los patos

Son estos ciclos los que, por su forma, han sido denominados como patos por los investigadores, mostrando, por ejemplo, que para todo $x$ entre $-2$ y $1$ , existe un valor de a para el cual existe un ciclo pato cuyo pico tiene la abscisa $x$ . Sin el apoyo de la modelización ANE, la existencia de estas trayectorias hubiera podido permanecer ignorada. De hecho, para observarlas no es suficiente tener $c$ pequeño y $a$ cercano a $1$ ; se puede mostrar que es necesario que $1-a$ esté muy cerca de $c/8$ ; más precisamente; que el cociente $(1-a-c/8)/c$ sea infinitamente pequeño. La existencia de estas trayectorias para sistemas de dos y tres dimensiones, ha encontrado diversas aplicaciones, más allá de su interés puramente matemático.

En todo caso se debe reconocer que, en general, aquellos nuevos resultados obtenidos gracias al uso del ANE han sido, con frecuencia, demostrados a continuación con métodos clásicos. Esto no es en sí sorprendente, ya que el IST es una extensión conservadora de la teoría de conjuntos: todo teorema de la teoría IST expresado con un enunciado clásico ya es un teorema de la teoría ZFC. Este hecho –la existencia de una demostración clásica alternativa–combinado con la sensación de regresión que da a muchos matemáticos el uso de estos infinitésimos de los que las matemáticas tuvieron tantas dificultades para liberarse, puede llevar a juzgar las construcciones derivadas del ANE como de poca utilidad. Los que practican el ANE rechazan estas objeciones. Insisten en el cambio de visión que promueve el ANE, en las intuiciones y modelizaciones que el ANE pueden favorecer, más en sintonía –según ellos– con el mundo real que las asociadas con el análisis clásico. A una visión del conjunto de los números reales como una entidad homogénea, oponen la visión no estándar que pone, en el corazón del sistema numérico, una distinción entre órdenes de magnitud que refleja la diversidad de escalas que considera la ciencia actual, así como los límites, necesariamente borrosos, entre estas escalas. También hacen hincapié en el potencial que ofrece el ANE, a través de los infinitésimos, en términos de modelos discretos para muchos ámbitos de aplicación. Para ellos estos logros merecen que el ANE sea plenamente reconocido.

En la enseñanza también se han dado varios intentos para desarrollar aproximaciones no estándar a la enseñanza del análisis elemental, ya sean basadas en la simplificación de la construcción de Robinson –como las de Keisler (1976) o de Heinle y Kleinberg (1979)–, ya sean inspiradas en el enfoque axiomático de Nelson (Deledicq y Diener, 1989). Pero, como Hodgson (1994) observó en la síntesis que presentó en el congreso ICME-7 en Quebec, ninguna de estas construcciones innovadoras ha logrado establecerse de manera duradera en un sistema de enseñanza. La situación marginal del ANE probablemente ha contribuido a ello, pero también el hecho de que, si se quiere hacer un uso productivo del análisis no-estándar, no basta con introducir el lenguaje infinitesimal, se debe aprender a manejar nuevas nociones y definiciones, familiarizarse con nuevas formas de razonamiento, construir nuevas referencias e intuiciones, desarrollar nuevos medios de control.

Así, finalmente, esta viñeta ilustra dos fenómenos frecuentes en la historia de las ciencias y de las matemáticas:

El hecho de que la integración de ideas intuitivas en teorías matemáticas rigurosas puede no ser posible sino gracias a otros avances científicos, a veces años e, incluso, siglos después que estas intuiciones demostraran ser fructíferas. Este ha sido el caso de la idea de infinitésimo, gracias al desarrollo de la lógica matemática en el siglo XX; pero también el de la idea intuitiva de límite, que es la base del análisis estándar en el siglo XIX, como se mencionó al principio de esta viñeta ;
El hecho de que diversas teorizaciones de una misma realidad pueden coexistir, ofreciendo perspectivas fructíferas y complementarias para darle sentido y trabajarla. Este es el caso del análisis estándar y del análisis no estándar, dos maneras diferentes, pero complementarias, de abordar el ámbito de las funciones y del análisis, y de pensar acerca de sus conexiones con el mundo real.

Por último, nos gustaría destacar que la construcción presentada aquí, el ANE, no es la única manera de dar un estatus matemático a los infinitésimos. Ha habido diversos intentos a lo largo de la historia (ver Borovik y Katz , 2012). El análisis infinitesimal suave, desarrollado a partir de las ideas de F.W. Lawvere en la Teoría de Categorías es, por ejemplo, otra reciente construcción: en ésta, un infinitésimo se define como un número distinto de cero cuyo cuadrado es cero (ver Bell, 2008).

Referencias:

Bell, J.L. (2008). A primer of infinitesimal analysis, 2nd edition. Cambridge : Cambridge University Press.
Borovik, B. & Katz, M. (2012) Who Gave you the Cauchy-Weierstrass Tale? The Dual History of Rigorous Calculus. Foundations of Science 17, no. 3, 245-276.
Berkeley, G. (1734). The Analyst. http://www.maths.tcd.ie/pub/HistMath/People/Berkeley/Analyst/
Benoît, E., Callot, J.L., Diener, F., & Diener. M. (1981). Chasse au canard. Collectanea Mathematica, 32.1, 38-74.
http://collectanea.ub.edu/index.php/Collectanea/article/view/3537/4216
Deledicq A., & Diener, M. (1989). Leçons de calcul infinitésimal. Collection U. Paris : Armand Colin.
Diener, M., & Diener, F. (Eds.). (1995). Non standard analysis in practice. Berlin : Springer Verlag.
Henle, J.M., & Kleinberg, E.M. (1979). Infinitesimal Calculus. Cambridge : MIT Press.
Hodgson, B. (1994). Le calcul infinitésimal. In, D.F. Robitaille, D.H. Wheeler et C. Kieran (Eds.), Choix de conférence du 7e Congrès international sur l’enseignement des mathématiques (ICME-7), pp. 157-170. Québec : Presses de l’Université Laval.
Document.
Keisler, H.J. (1976). Elementary calculus : An infinitesimal approach. Boston : Prindle, Weber & Schmidt.
Lakatos, I. (1978): Cauchy and the continuum: the significance of nonstandard analysis for the history and philosophy of mathematics. Math. Intelligencer 1, no. 3, 151–161 (paper originally presented in 1966).
Lutz, R. & Goze, M. (1982). Non standard analysis : a practical guide with applications. Springer Lecture Notes in Mathematics, vol. 881. Berlin : Springer.
Marquis de l’Hôpital, G.F.A. (1696). Analyse des infiniment petits pour l’intelligence des lignes courbes. Paris : Imprimerie Royale.
Nelson, E. (1977). Internal set Theory, a new approach to NSA, Bull. Amer. Math. Soc., vol. 83, no 6,‎ 1165-1198.
Robinson, A. (1996). Non standard analysis. North Holland, Amsterdam.
Skolem, Th. (1934). Über die Nicht-charakterisierbarkeit der Zahlenreihe mittels endlich oder abzählbar unendlich vieler Aussagen mit ausschliesslich Zahlenvariablen. Fundam. Math. 23, 150-161

$^i$ «El alcance de este cálculo es enorme: sirve tanto a las curvas mecánicas como a las geométricas; los signos radicales le son indiferentes y, a menudo, convenientes; se extiende a tantas indeterminadas como se quiera; la comparación de infinitamente pequeños de todo tipo le es igualmente fácil. De esto surgen una infinidad de descubrimientos sorprendentes en relación con las tangentes tanto curvas como rectas; sobre cuestiones de máximos y mínimos; sobre puntos de inflexión y cúspides de curvas; sobre envolventes y cáusticas por reflexión o refracción, etc. como se explicará en este libro.»
$^{ii}$ Axiomática de Zermelo-Fraenkel complementada con el axioma de elección. (http://en.wikipedia.org/wiki/Zermelo–Fraenkel_set_theory).
$^{iii}$ El axioma de idealización dice que para toda relación binaria $R$ clásica (es decir, que se expresa sin el uso del predicado $st$ ), las dos proposiciones siguientes son equivalentes: (i) para todo conjunto estándar finito $F$ , existe un $x$ tal que, para todo $y$ de $F$ , $R(x,y)$ ; (ii) existe un $x$ tal que, para todo $y$ estándar, $R(x,y)$ .
El axioma de estandarización dice que, para toda propiedad $P$ y todo conjunto estándar $X$ , existe una parte estándar $Y$ de $X$ cuyos elementos estándar son exactamente los elementos de $X$ que satisfacen $P$ . Este axioma vale tanto para propiedades $P$ clásicas o no.
El axioma de transferencia dice que para toda propiedad clásica $P$ , $P(x)$ es verdadera para todo $x$ si y solo si $P(x)$ es verdadera para todo $x$ estándar.
$^{iv}$ Basta aplicar el axioma de transferencia a la propiedad $P(x)$ : $x \in E1 \Leftrightarrow x \in E2$ .
$^{v}$ En el primer caso, se aplica el axioma de idealización en $\mathbb{N}$ a la relación binaria $x<y$ ; en el segundo caso, se aplica, en el conjunto infinito considerado, a la relación binaria $x \neq y$ .
$^{vi}$ En esta tabla, todos los objetos: $(u_n)$ , $l$ , $f$ , $a$ , $I$ se suponen estándar.
$^{vii}$ En este enunciado, $I$ , $f$ , $a$ y $b$ se suponen estándar.