La revanche des infinitésimaux

Vignette écrite par Michèle Artigue.

Les infinitésimaux ont joué un rôle essentiel dans l’émergence et le développement du calcul différentiel et intégral. La productivité évidente de ce calcul n’empêcha pas cependant des débats récurrents et parfois féroces sur la nature de ces objets et la légitimité de leur usage. A la fin du 19ème siècle, quand la construction des nombres réels à partir des entiers, la définition moderne de la notion de limite, eurent fourni des fondations solides au calcul différentiel et intégral, les infinitésimaux et la métaphysique qui les avait entourés furent rejetés et leur usage perçu synonyme de pratiques peu rigoureuses désormais révolues. Pourtant, le langage des infinitésimaux continua à être utilisé par exemple en physique et, même en mathématiques, il n’a jamais complètement disparu du discours informel, de la pensée heuristique de nombre de chercheurs.

Alors ce langage est-il réellement incompatible avec la rigueur mathématique ? Et qu’offre-t-il d’intéressant, de spécifique qui explique sa permanence ? L’Analyse non standard développée au 20ème siècle a permis de répondre à ces questions, et aux infinitésimaux de prendre leur revanche.

Du calcul infinitésimal à l’analyse non standard

Dans la préface du premier traité d’analyse infinitésimale publié en 1696, son auteur, le Marquis de l’Hôpital vante la puissance et la facilité du nouveau calcul que les infinitésimaux permettent :

Figure 1 : Couverture et extrait de la préface du traité du Marquis de l’Hôpital

Mais très vite, des débats se développent autour de ces objets et de leurs usages. Dans un texte célèbre publié en 1734, The analyst, George Berkeley fait ainsi une critique féroce de l’usage de ces infinitésimaux ou incréments évanescents dans le calcul différentiel et Jean Le Rond d’Alembert, dans l’Encyclopédie Méthodique de 1751, propose de s’en affranchir en s’appuyant sur l’idée de limite. Au tournant du 20ème siècle, avec le développement de l’analyse moderne, cela semble chose faite. Pourtant, un demi-siècle plus tard, les travaux du logicien Abraham Robinson vont réhabiliter les infinitésimaux et les pratiques associées.

Abraham Robinson montre en effet que le langage des infinitésimaux est tout à fait compatible avec la rigueur mathématique. Le logicien Thoralf Skolem avait déjà montré dès 1934 que l’ensemble obtenu par addition d’unités successives à partir de $0$ ne pouvait être le seul modèle de l’axiomatique de Peano, qu’il existait donc des modèles différents dits non standard de cette arithmétique. En 1961, Abraham Robinson montre, lui, par une construction à base d’ultraproduits, l’existence d’un modèle non standard des nombres réels contenant des nombres « infiniment grands » et « infiniment petits ». Il donne ainsi naissance à l’Analyse Non Standard (ANS). Puis Edward Nelson en 1977 trouve le moyen d’axiomatiser l’ANS. Pour cela, il ajoute au langage de la théorie des ensembles un symbole de prédicat à une place, $st(x)$ , exprimant qu’un objet $x$ est standard, et à l’axiomatique ZFC $^{i}$ de cette théorie, trois axiomes : les axiomes d’idéalisation, de standardisation et de transfert $^{ii}$ , ce qui rend l’ANS plus aisément manipulable. C’est sur cette axiomatisation dénommée IST (Internal Set Theory) que nous nous appuyons dans cette vignette.

Ces trois axiomes ont des conséquences importantes. Il découle par exemple de l’axiome de transfert que deux ensembles standard E1 et E2 sont égaux si et seulement si ils ont les mêmes éléments standard $^{iii}$ . Il découle de ce même axiome que s’il existe un $x$ qui vérifie une propriété classique $P$ , c’est à dire une propriété qui peut s’exprimer sans utiliser le prédicat $st$ , alors il existe nécessairement un $x$ standard qui la vérifie. Les objets que l’on peut définir de manière unique par une formule classique sont ainsi nécessairement des objets standard. Les nombres et les objets usuels que nous fréquentons en mathématiques : les nombres $\pi$ , $e$ , les fonctions trigonométriques et exponentielles, sont des objets standards, tout comme l’ensemble vide, l’ensemble $\mathbb{N}$ des entiers et l’ensemble $\mathbb{R}$ des nombres réels.

Mais être un ensemble standard n’implique pas avoir uniquement des éléments standard. Il découle en fait de l’axiome d’idéalisation qu’il existe un entier supérieur à tous les entiers standard, nécessairement non standard et que, plus généralement, tout ensemble infini contient nécessairement au moins un élément non standard $^{iv}$ . $\mathbb{N}$ et $\mathbb{R}$ sont ainsi des ensembles standard qui contiennent des éléments non standard. Comment se les représenter ?

Dans $\mathbb{N}$ , tous les entiers standard précèdent les entiers non standard. Dans $\mathbb{R}$ , la situation est un peu plus compliquée. On distingue en fait, selon leur taille, trois types de réels :

les réels très petits ou infinitésimaux (positifs et négatifs), ceux dont la valeur absolue est inférieure à tout réel standard strictement positif,
les réels très grands ou infiniment grands (positifs et négatifs), ceux dont la valeur absolue est supérieure à tout réel standard positif,
et entre les deux, les réels à échelle humaine pourrait-on dire, que l’on appelle souvent appréciables.

Si un réel est infinitésimal ou appréciable, on dit qu’il est limité. Si un réel est infiniment grand, son inverse est un infinitésimal et ils sont l’un et l’autre nécessairement non standard. En revanche, les réels appréciables peuvent-être standard ou non-standard. Considérons par exemple le réel $1$ , en lui ajoutant un infinitésimal non nul $\alpha$ , on obtient le réel $1+\alpha$ , lui aussi appréciable mais non standard et infiniment proche de $1$ . Autour de chaque réel standard, existe ainsi un nuage de réels non standard qui en sont infiniment proches. Pour en rendre compte, on introduit une nouvelle relation. On dira que $x$ est infiniment voisin de $y$ si $x-y$ est un infinitésimal, ce que l’on note $x \simeq y$ , et l’on appellera halo d’un réel la collection des réels qui en sont infiniment proches. Les infinitésimaux sont en fait le halo de $0$ et tout réel $x$ appréciable appartient au halo d’un réel standard unique, que l’on appelle sa partie standard. On peut se représenter la droite réelle comme dans la figure 2, avec une frontière qui n’est pas clairement marquée entre les réels appréciables et les infiniment grands, la collection des réels appréciables n’ayant pas de plus grand élément, ni celle des infiniment grands positifs de plus petit élément.

Figure 2 : Représentation de la droite réelle non standard

Des règles de calcul prenant en compte les différences d’ordre de grandeur des nombres prolongent celles de l’arithmétique. Ainsi, en notant $ip$ les infinitésimaux, $app$ les appréciables et $ig$ les infiniment grands, on a par exemple : $ip.app=ip$ , $ip+app=app$ , $ip.ip=ip$ et $ip+ig=ig$ , et nous invitons le lecteur à compléter lorsque possible les cases des deux tableaux suivants.

Rendered by QuickLaTeX.com

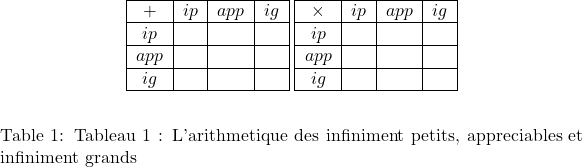
Ainsi, l’ensemble des réels vérifie-t-il toujours le principe d’Archimède : si $a$ et $b$ sont des réels positifs tels que $0<a<b$ , il existe un entier $n$ tel que $na>b$ , mais bien sûr si $a$ est un infiniment petit et si $b$ ne l’est pas, $n$ sera infiniment grand.

L’ANS et les notions de base de l’analyse

Dans ce cadre de l’ANS, les notions de base de l’analyse mathématique : limites, continuité, dérivabilité, intégrabilité, se formalisent très simplement pour les objets standard, comme le montre le tableau ci-après $^v$ :

Rendered by QuickLaTeX.com

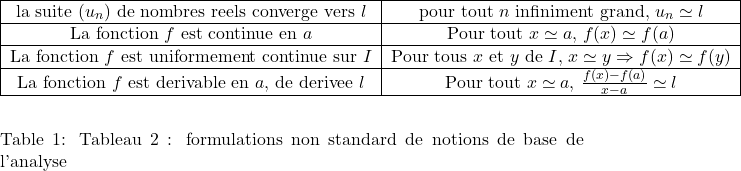
Ces formalisations simples, sans alternances de quantificateurs, et les idées qui les sous-tendent, permettent des démonstrations simplifiées de bon nombre de théorèmes classiques. L’encadré ci-après propose ainsi une démonstration du théorème des valeurs intermédiaires.

Théorème des valeurs intermédiaire $^{vi}$ s : Soient $I$ un intervalle de $\mathbb{R}$ , $f$ une fonction à valeurs réelles continue sur $I$ , $a$ et $b$ deux réels de $I$ avec $a < b$ , pour tout $y$ compris entre $f(a)$ et $f(b)$ , il existe un réel $c$ de $[a,b]$ tel que $f(c)=y$ .
Preuvee : on peut, sans restreindre la généralité, supposer $y=0$ et $f(a)<0<f(b)$ pour démontrer le théorème. Soit $\omega$ infiniment grand et la subdivision de $[a,b]$ de pas $(b-a)/\omega$ ( $x_0=a$ , … , $x_n=a+n(b-a)/\omega$ ,… , $x_{\omega}=b$ ). Soit $m$ le plus petit indice tel que $f(xm)>0$ . On a $m \neq 0$ par hypothèse et $x_m$ est un réel limité puisque compris entre $a$ et $b$ . Prenons pour $c$ sa partie standard. Alors $f(x_{m-1}) \leq 0$ et $f(x_m)>0$ mais $x_{m-1} \simeq x_m$ puisque le pas de subdivision est infinitésimal et $x_m \simeq c$ , donc $f$ étant continue en $c$ , $f(c) \simeq f(x_{m-1}) \simeq f(x_m)$ . Comme $f(c)$ est standard, $f(c)=0$ .

L’ANS permet aussi de justifier les techniques de découpage en tranches infinitésimales toujours utilisées hors de la communauté mathématique pour calculer des aires, volumes, moments d’inertie, centres de gravité…, ou pour modéliser des situations à l’aide d’équations différentielles. L’exemple ci-après en est une illustration particulièrement simple.

Calcul du volume de la sphère :

Soit $S$ une sphère de rayon $R$ . On découpe la sphère en tranches d’épaisseur $dz$ infinitésimale. Le volume $dV$ de la tranche située à la hauteur $z$ est approximativement celui du $cylindre$ de rayon $\sqrt{R^2 - z^2}$ et de hauteur $dz$ .
$dV = \pi (R^2 - z^2)dz$
d’où, par sommation,
$V=\int_{-R}^{R} \pi(R^2 - z^2) dz$
$V=\left[ \pi (R^2 z - z^3 /3) \right]_{-R}^{R}$
et finalement $V=\frac{4 \pi R^3}{3}$ .

Figure 3 : Le volume de la sphere

La somme des volumes des cylindres infinitésimaux n’est autre que la somme de Cauchy associée au découpage infinitésimal de pas $dz$ de l’intervalle $[-R,R]$ pour la fonction aire $S(z)=\pi (R^2-z^2)$ . La partie standard de cette somme est donc égale, par définition non standard de l’intégrale d’une fonction continue, à l’intégrale $\int_{-R}^R S(z) dz$ .
En revanche, le fait que cette intégrale donne bien le volume de la sphère repose sur le fait que l’approximation proposée donne bien un équivalent du volume de la tranche, pas seulement qu’elle en est infiniment proche. Ce ne serait plus le cas si l’on utilisait cette même approximation par des cylindres pour calculer l’aire de la sphère par exemple.

La nécessité d’une certaine vigilance

Manipuler des objets non standard demande cependant une certaine vigilance. Par exemple, en étendant la définition ci-dessus de la continuité à une fonction et un réel quelconques, standard ou non, on obtient une notion : la $S$ -continuité en un point, qui ne correspond pas forcément à notre vision des fonctions continues. Par exemple, la fonction en escalier qui vaut $0$ sur les réels négatifs et $\alpha$ sur les réels positifs ou nuls, avec $\alpha$ infiniment petit non nul, est $S$ -continue en $0$ puisque l’image de tout infinitésimal positif est l’infinitésimal $\alpha$ . En revanche, la fonction carré n’est, elle, pas $S$ -continue en $\omega$ , si $\omega$ est infiniment grand, puisque $(\omega+1/\omega)^2=\omega^2+1/\omega^2+2$ n’est pas infiniment proche de $\omega^2$ . En fait, pour une fonction standard, la $S$ -continuité en tout point de $\mathbb{R}$ équivaut à la continuité uniforme sur $\mathbb{R}$ , et le calcul que nous venons de faire pour la fonction carré montre, très simplement, que cette fonction, si elle est bien continue sur $\mathbb{R}$ , n’y est pas uniformément continue.

L’usage de l’ANS demande aussi d’être vigilant dans l’utilisation du principe de récurrence. Sous sa forme usuelle, il s’applique aux propriétés classiques, c’est une des conséquences de l’axiome de transfert, mais non au-delà. Considérons le raisonnement suivant, souvent présenté comme paradoxal :

Soit $P$ la propriété « Etre standard ». $P(0)$ est vraie et, pour un entier $n$ quelconque, si $P(n)$ est vraie alors $P(n+1)$ est vraie. Donc, pour tout $n$ , $P(n)$ est vraie et tous les entiers sont standard.

Le principe de récurrence y est appliqué à un énoncé non classique puisqu’écrit avec le prédicat $st$ . Le raisonnement n’est en rien paradoxal. Il est simplement non valide. En fait, on démontre que, pour une propriété quelconque $P$ , on a simplement le principe de récurrence réduit suivant : Si $P(0)$ est vraie et si, pour tout entier $n$ , $P(n)$ implique $P(n+1)$ , alors $P$ est vraie pour tout entier standard.

Les potentialités de l’ANS : une question toujours débattue

On le voit donc, l’ANS réhabilite les infinitésimaux, les modes de calcul et les intuitions qu’ils portent, mais ceci au prix d’un certain travail et d’une certaine vigilance. Alors que gagne-t-on réellement avec l’ANS ? La question est toujours en débat, comme le montre par exemple le blog du mathématicien Terence Tao auquel nous avons accédé en préparant cette vignette L’ANS a été utilisée dans des domaines mathématiques divers : topologie, probabilités, systèmes dynamiques notamment. Elle a aussi nourri des modélisations intéressantes en automatique, écologie, économie par exemple. En France, par exemple, à l’initiative de Georges Reeb, une communauté s’est développée dès la fin des années 70 ayant à son actif des résultats originaux dans de nombreux domaines (cf. (Lutz et Goze, 1982), (Diener & Diener, 1995). Un des plus connus est la découverte des trajectoires appelées « canards » dans des champs de vecteurs lents-rapides, en deux puis trois dimensions. Nous le présentons à titre d’exemple sans rentrer cependant dans les détails techniques de son traitement non standard. Le lecteur, peu familier avec les équations différentielles, pourra sauter cette partie.

Les trajectoires « canard »

Considérons l’équation différentielle $cx''+(x^2-1)x'+x-a=0$ , avec $a \geq 0$ et $c>0$ . Une étude classique de cette équation montre que si $a<1$ , l’équation admet une solution périodique unique qui est un cycle limite attractif. Cette solution périodique disparaît pour $a=1$ et il existe alors un état stationnaire attractif $x=a$ . Le phénomène des trajectoires canards qui précède cette bifurcation de la dynamique, connue sous le nom de bifurcation de Hopf, a été mis en évidence pour des valeurs de $c$ très petites et de a très proche de $1$ . Une modélisation non standard, supposant c infiniment petit a permis d’identifier le phénomène et d’en caractériser les conditions d’apparition.

On ramène d’abord l’équation à un système, et ceci de deux façons différentes : soit en posant $u=cx'+F(x)$ avec $F(x)=x^3/3-x$ , une transformation classique pour étudier ce type d’équation dit de Lienard, soit de façon classique, en posant $v=x'$ . D’où les deux systèmes, où $\omega=1/c$ est un réel infiniment grand :

$\left\{ \begin{array}{cl} x' &= \omega (u-F(x)), \\ u' &= a-x \end{array}\right$

$\left\{ \begin{array}{cl} x' &= \omega (u-F(x)), \\ v' &= \omega(a-x-(x^2 -1)v) \end{array}\right$

Les champs associés dans les plans $(x,u)$ et $(x,v)$ sont reproduits dans les figures 1 et 2 extraites de (Benoît et al., 1981). Ce sont des champs lents-rapides. Par exemple, le champ du plan $(x,u)$ ou plan de Lienard est quasiment horizontal en dehors du halo de la cubique $C$ d’équation $u=F(x)$ dont les parties croissantes sont, vu le sens des flèches horizontales, attractives tandis que la partie décroissante est répulsive. Les doubles flèches rappellent que ces parties quasi-horizontales sont parcourues avec une vitesse infiniment grande. On montre, en combinant des techniques d’analyse classique et d’analyse non standard, notamment l’utilisation de changements d’échelle, par des grossissements de rapport infiniment grand suivant une direction, dans les plans $(x,u)$ et $(x,v)$ que, lorsque $a<1$ mais non dans le halo de $1$ , il existe un grand cycle unique attractif (figure 3). Dans le plan $(x,u)$ , une particule suivant ce cycle, partant par exemple d’un point $M$ non situé dans le halo de $C$ , rejoint ce halo quasi-horizontalement à une vitesse infiniment grande puis longe $C$ , en restant dans ce halo, à une vitesse appréciable $x' \simeq (a-x)/(x^2-1)$ jusqu’à arriver dans le halo de son minimum local $S-$ . Ensuite elle reprend sa course quasiment horizontale jusqu’à rentrer à nouveau dans le halo de $C$ et la longer jusqu’au halo du maximum local $S+$ , avant de repartir horizontalement.

Lorsque $a \simeq 1$ , la situation se complique car des branches séparées de la courbe $Ha$ associée à $v'=0$ dans le plan des phases de l’équation, deviennent infiniment proches. Il s’ensuit dans le plan $(x,u)$ qu’une solution qui a longé $C$ jusqu’au halo de $S-$ peut, pour certaines valeurs de $a$ , longer une portion de la partie répulsive de $C$ , avant de devenir quasi-horizontale et rejoindre le halo de la partie attractive de $C$ (figure 4).

Figure 4 : Morphologie des canards

C’est à ces cycles que, vu leur forme, les chercheurs ont donné le nom de canard, montrant par exemple que, pour tout $x$ entre $-2$ et $1$ , il existe une valeur de $a$ tel qu’il existe un cycle canard dont le bec ait pour abscisse $x$ . Sans l’aide d’une modélisation ANS, l’existence de ces trajectoires aurait pu rester ignorée. En effet, pour les observer, il ne suffit pas que $c$ soit petit et a voisin de $1$ , on montre qu’il faut que $1-a$ soit très proche de $c/8$ , plus précisément que le quotient $(1-a-c/8)/c$ soit infiniment petit. L’existence de ces trajectoires canards, mise en évidence dans des systèmes en deux et trois dimensions, au-delà de son pur intérêt mathématique, a trouvé diverses applications.

Il faut cependant souligner que les résultats nouveaux que l’ANS a permis d’obtenir ont été souvent ensuite redémontrés par des méthodes classiques. Ce n’est en soi pas étonnant puisque l’ANS est une extension conservative de la théorie des ensembles : tout théorème de la théorie IST dont l’énoncé est classique est déjà un théorème de ZFC. Combiné avec le sentiment de régression que donne à de nombreux mathématiciens le recours à ces infinitésimaux dont les mathématiques ont eu tant de mal à se débarrasser, ceci amène souvent à juger cette construction peu utile. Ceux qui pratiquent l’ANS récusent ces objections. Ils insistent sur le changement de vision qu’amène l’ANS, les intuitions et modélisations qu’elle peut nourrir, plus adaptées selon eux à la réalité du monde que celles associées à l’analyse classique. A une vision de l’ensemble des nombres réels comme entité homogène, ils opposent la vision non standard qui met au cœur du système numérique une distinction entre ordres de grandeur, reflétant la diversité des échelles que considère la science actuelle, ainsi que les frontières nécessairement floues entre ces échelles. Ils insistent aussi sur les potentialités offertes par l’ANS via les infinitésimaux en termes de modélisations discrètes pour de nombreux domaines d’application. Pour eux, ces gains méritent que l’ANS soit pleinement reconnue.

Dans l’enseignement aussi, diverses tentatives ont été faites pour développer des approches non standard de l’enseignement de l’analyse élémentaire, basées sur des simplifications de la construction de Robinson comme celles de Keisler (1976) ou de Henle et Kleinberg (1979) ou inspirées de l’approche axiomatique de Nelson (Deledicq et Diener, 1989). Mais, comme le soulignait Hogdson (1994) dans la synthèse de ces travaux qu’il avait présentée au congrès ICME-7 à Québec, aucune de ces constructions innovantes n’a réussi à s’imposer durablement dans l’enseignement. Le statut marginal de l’ANS n’y est sans doute pas étranger, mais aussi le fait que si l’on veut faire un usage productif de l’analyse non standard, il ne suffit pas de parler d’infinitésimaux, il faut apprendre à manipuler de nouvelles notions et définitions, se familiariser avec de nouveaux modes de raisonnement, se construire de nouvelles références et intuitions, développer de nouveaux moyens de contrôle.

Cette vignette illustre finalement deux phénomènes fréquents dans l’histoire des sciences et des mathématiques :

le fait que l’intégration dans des théories mathématiques rigoureuses d’idées intuitives peut ne devenir accessible, grâce à d’autres avancées scientifiques, que bien des années, voire des siècles, après que ces intuitions se soient révélées fécondes. Ce fut le cas pour l’idée d’infinitésimal grâce au développement de la logique mathématique au 20ème siècle, mais aussi pour l’idée intuitive de limite qui est à la base de l’analyse standard, au 19e siècle, comme rappelé au début de cette vignette ;
le fait aussi que plusieurs théorisations d’un même domaine de réalité peuvent coexister, offrant des perspectives fructueuses et complémentaires pour faire sens de ce domaine et le travailler. C’est bien le cas pour l’analyse standard et l’analyse non standard, deux façons différentes mais complémentaires d’approcher le champ des fonctions et de l’analyse, et de penser ses connections avec le monde réel.

Nous voudrions enfin souligner que la construction présentée ici, celle de l’ANS, n’est pas la seule possible pour donner un statut mathématique aux infinitésimaux. Diverses tentatives se sont succédées au fil de l’histoire (voir Borovik et Katz, 2012). L’analyse infinitésimale lisse, développée à partir des idées de F.W. Lawvere en théorie des catégories, est par exemple une autre construction récente : un infinitésimal y est défini comme un nombre non nul dont le carré est nul (voir Bell, 2008).

Références :

Bell, J.L. (2008). A primer of infinitesimal analysis, 2nd edition. Cambridge : Cambridge University Press.
Borovik, B. & Katz, M. Who Gave you the Cauchy-Weierstrass Tale? The Dual History of Rigorous Calculus. Foundations of Science 17 (2012), no. 3, 245-276.
Berkeley, G. (1734). The Analyst. http://www.maths.tcd.ie/pub/HistMath/People/Berkeley/Analyst/
Benoît, E., Callot, J.L., Diener, F., & Diener. M. (1981). Chasse au canard. Collectanea Mathematica, 32.1, 38-74.
http://collectanea.ub.edu/index.php/Collectanea/article/view/3537/4216
Deledicq A., & Diener, M. (1989). Leçons de calcul infinitésimal. Collection U. Paris : Armand Colin.
Diener, M., & Diener, F. (Eds.). (1995). Non standard analysis in practice. Berlin : Springer Verlag.
Heinle, J.M., & Kleinberg, E.M. (1979). Infinitesimal Calculus. Cambridge : MIT Press.
Hodgson, B. (1994). Le calcul infinitésimal. In, D.F. Robitaille, D.H. Wheeler et C. Kieran (Eds.), Choix de conférence du 7e Congrès international sur l’enseignement des mathématiques (ICME-7), pp. 157-170. Québec : Presses de l’Université Laval.
Document.
Keisler, H.J. (1976). Elementary calculus : An infinitesimal approach. Boston : Prindle, Weber & Schmidt.
Lakatos, I.: Cauchy and the continuum: the significance of nonstandard analysis for the history and philosophy of mathematics. Math. Intelligencer 1 (1978), no. 3, 151–161 (paper originally presented in 1966).
Lutz, R. & Goze, M. (1982). Non standard analysis : a practical guide with applications. Springer Lecture Notes in Mathematics, vol. 881. Berlin : Springer.
Marquis de l’Hôpital, G.F.A. (1696). Analyse des infiniment petits pour l’intelligence des lignes courbes. Paris : Imprimerie Royale.
Nelson, E. (1977). Internal set Theory, a new approach to NSA, Bull. Amer. Math. Soc., vol. 83, no 6,‎ 1165-1198.
Robinson, A. (1996). Non standard analysis. North Holland, Amsterdam.
Skolem, Th. (1934). Über die Nicht-charakterisierbarkeit der Zahlenreihe mittels endlich oder abzählbar unendlich vieler Aussagen mit ausschliesslich Zahlenvariablen. Fundam. Math. 23, 150-161

$^i$ Axiomatique de Zermelo-Fraenkel complétée par l’axiome du choix.
$^{ii}$ L’axiome d’idéalisation dit que pour toute relation binaire $R$ classique (c’est à dire s’exprimant sans recours au prédicat $st$ ), les deux propositions suivantes sont équivalentes : (i) pour tout ensemble standard fini $F$ , il existe un $x$ tel que, pour tout $y$ de $F$ , on ait $R(x,y)$ ; (ii) il existe un $x$ tel que, pour tout $y$ standard, $R(x,y)$ .
L’axiome de standardisation dit que, pour toute propriété $P$ et tout ensemble standard $X$ , il existe une partie standard $Y$ de $X$ dont les éléments standards sont exactement les éléments de $X$ qui satisfont $P$ . Cet axiome vaut que $P$ soit une propriété classique ou non.
L’axiome de transfert dit que pour toute propriété classique $P$ , $P(x)$ est vraie pour tout $x$ si et seulement si $P(x)$ est vraie pour tout $x$ standard.
$^{iii}$ Il suffit d’appliquer l’axiome de transfert à la propriété $P(x)$ : $x \in E1 \Leftrightarrow x \in E2$
$^{iv}$ Dans le premier cas, on applique l’axiome d’idéalisation dans $\mathbb{N}$ à la relation binaire $x<y$ ; dans le second cas, on l’applique dans l’ensemble infini considéré à la relation binaire $x \neq y$
$^v$ Dans ce tableau, tous les objets : $(u_n)$ , $l$ , $f$ , $a$ , $I$ sont supposés standard.
$^{vi}$ Dans cet énoncé, $I$ , $f$ , $a$ et $b$ sont supposés standard.