Matrices et Images Numériques

Publié le mai 5, 2012 par admin

Vignette écrite par Dirce Uesu Pesco et Humberto José Bortolossi.
Les images publiées sur les sites internet et les photographies prises avec un téléphone portable sont des exemples d’ images numériques. Il est possible de représenter ce type d’ image par des matrices. Par exemple, la petite image de Félix le Chat peut être représentée par une matrice de taille 35 \times 35 dont les éléments sont des 0 et des 1. L’ élément indique la couleur du pixel : 0 pour un pixel noir et 1 pour un pixel blanc (un pixel est le plus petit élément graphique d’une image matricielle, qu ine peut prendre qu’une seule couleur à la fois). Les images numériques qui n’ utilisent que deux couleurs sont appelées images binaires ou images booléennes.

Figure 2: La matrice correspondant à Felix le Cat

Les images en niveau de gris peuvent aussi être représentées par des matrices. Chaque élément détermine l’ intensité du pixel correspondant. Pour des raisons pratiques, la majorité des archives numériques actuelles utilisent des nombres entiers compris entre 0 (pour un pixel noir, couleur d’ intensité minimale) et 255 (pour un pixel blanc, couleur d’ intensité maximale), ce qui donne un total de 256 = 2^8 nuances de gris différentes (ce nombre est acceptable pour des images de sites internet, par exemple. Cependant, certaines utilisations, comme l’ imagerie médicale, nécessitent plus de nuances de gris afin de reproduire une image avec plus de détails et d’ éviter des erreurs d’ approximations dans des calculs).

Les images en couleurs, en revanche, peuvent être représentées par trois matrices. Chaque matrice détermine la quantité de rouge , de vert et de bleu qui constitue l’ image. Ce modèle de couleur est appelé RVB (il existe de nombreux autres modèles de couleur, pour diverses utilisations: La quadrichromie ou CMJN (en imprimerie), Y’IQ (pour la télévision analogique NTSC), etc). Les éléments de ces matrices sont des nombres entiers compris entre 0 et 255 qui déterminent l’ intensité de la couleur de la matrice pour le pixel correspondant. Ainsi, avec le modèle RVB, il est possible de représenter 2563 = 2^{24} = 16777216 couleurs différentes.

Figure 3: Image originale, composantes Rouge, Verte et Bleue

Traitement d’ images à l’ aide d’ Opérations Matricielles

Une fois qu’ une image est représentée par des matrices, on peut se demander si des opérations sur leurs éléments influencent l’ image correspondante. Par exemple, si on considère l’ image binaire A (ci-dessous) comme une matrice A = (a_{i,j}), alors l’ image B correspond à la matrice transposée de A: B = (b_{i, j}) = (a_{j, i}) = A^{T}. L’ image H, en revanche, correspond à la matrice (a_{j, 35 - i + 1}). Essayez de découvrir la relation avec A pour les autres images!

Figure 4: Transformations de matrice

Un autre exemple: Si on arrange de façon arithmétique les matrices R, V et B des images en couleurs, on obtient une version de l’ image en niveau de gris (les valeurs sont arrondies à l’ entier le plus proche):

Figure 5: Moyenne arithmétique des composantes d'une image

Avec les opérations de multiplication par un scalaire (nombre réel) et d’ addition de matrices, il est possible de créer un effet de transition d’ image, utilisé régulièrement dans les diaporamas et présentations PowerPoint par exemple. Plus précisément, si on considère deux images en niveau de gris, de la même taille, repésentées par les matrices A et Z. Pour chaque scalaire t in the interval [0, 1], on définit la matrice

    \[M(t) = (1 - t) A + t Z.\]

On remarque que M(0) = A, M(1) = Z et pour chaque t entre 0 et 1, les éléments de la matrice M(t) sont compris entre les éléments respectifs des matrices A et Z. Par conséquent, quand t varie entre 0 to 1, la matrice M(t) varie entre A et Z. Dans le cas d’ images en couleurs, la transformation ci-dessus doit être appliquée aux matrices R, V et B qui composent l’ image.

Figure 6: M(0) = A, M(0.13), M(0.25), M(0.38), M(0.50), M(0.63), M(0.75), M(0.88), M(1)=Z

La multiplication de matrices a aussi des applications dans le traitement des images numériques. Bien que notre prochain exemple soit plus complexe (car basé sur des techniques d’algèbre linéaire enseignées dans les universités), nous pensons qu’il sera intéressant aux yeux des lecteurs. Les détails sont disponibles dans [Lay, 2011] et [Poole, 2005]. On considère par exemple la décomposition en valeurs singulières (ou décomposition SVD, de l’ anglais Singular Value Decomposition), qui consiste à écrire une matrice A_{m \times n} comme le produit de trois matrices:

    \[A_{m \times n}^{\vphantom{T}} = U_{m \times m}^{\vphantom{T}} s_{m \times n}^{\vphantom{T}} V_{n \times n}^{T},\]

où U et V sont des matrices orthogonaless (c’ est-à-dire que U^{T} U et V^{T}V sont les matrices identité de tailles m \times m et n \times n respectivement) et S est une matrice dont les éléments s_{i, j} sont nuls si i \not = j, et s_{1, 1} \geq s_{2, 2} \geq \cdots \geq s_{k, k} \geq 0, avec k = \min\{m, n\}. Voici un exemple d’ une telle décomposition:

    \[A = \left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \end{array}\right] = U S V^{T}\]

    \[= \left[ \begin{array}{rr} \displaystyle -\frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{2}}{2} \vspace*{0.5ex} \\ \displaystyle \frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{2}}{2} \end{array} \right] \left[ \begin{array}{rrr} \sqrt{3} & 0 & 0 \\ 0 & 1 & 0 \end{array} \right] \left[ \begin{array}{rrr} \displaystyle \frac{\sqrt{6}}{6} & \displaystyle -\frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{3}}{3} \vspace*{0.5ex} \\ \displaystyle -\frac{\sqrt{6}}{3} & 0 & \displaystyle \frac{\sqrt{3}}{3} \vspace*{0.5ex} \\ \displaystyle \frac{\sqrt{6}}{6} & \displaystyle \frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{3}}{3} \end{array} \right]^{T}. $ } }\]

Il est possible de démontrer que toute matrice possède une décomposition en valeurs singulières. Par ailleurs, il existe des algorithmes permettant de calculer une telle décomposition par ordinateur. Le point clé de cet exemple consiste à remarquer que si \textbf{u}_{1}, \textbf{u}_{2}, \ldots, \textbf{u}_{m} sont les colonnes de la matrice U et \textbf{v}_{1}, \textbf{v}_{2}, \ldots, \textbf{v}_{n} sont les colonnes de la matrice V, alors

    \[A = USV^{T} = s_{1, 1} \textbf{u}_{1} \textbf{v}_{1}^{T} + s_{2, 2} \textbf{u}_{2} \textbf{v}_{2}^{T} + \cdots + s_{k, k} \textbf{u}_{k} \textbf{v}_{k}^{T}.\]

Pourquoi? Supposez que A, une image en niveau de gris de taille 1000 \times 1000, doive être transmise d’ un satellite à un laboratoire sur Terre. En principe le satellite devrait avoir à envoyer un million de nombres. Cependant, seulement les premiers éléments s_{i, i} de la matrice S de la matrice S de la décomposition en valeurs singulières de A sont significatifs (le reste est “négligeable”), assez pour que le satellite n’ envoie que, disons, les 20 premières colonnes de U et de V, et les 20 premiers éléments s_{i, i} (pour un total de seulement 20 \cdot 1000 + 20 \cdot 1000 + 20 = 40020 nombres à envoyer). Quand il recevra ces données, le laboratoire sur Terre devra calculer la matrice s_{1, 1} \textbf{u}_{1} \textbf{v}_{1}^{T} + s_{2, 2} \textbf{u}_{2} \textbf{v}_{2}^{T} + \cdots + s_{20, 20} \textbf{u}_{20} \textbf{v}_{20}^{T} qui donnera une approximation de l’ image originale.

Par exemple, l’ image ci-dessous du mathématicien Felix Christian Klein (1849-1925) a 720 \times 524 = 377 280 pixels.

Figure 7: Felix Klein

A partir de la décomposition en valeurs singulières de la matrice correspondante, on peut calculer les matrices s_{1, 1} \textbf{u}_{1} \textbf{v}_{1}^{T} + s_{2, 2} \textbf{u}_{2} \textbf{v}_{2}^{T} + \cdots + s_{r, r} \textbf{u}_{r} \textbf{v}_{r}^{T} pour r = 1, 5, 10 et 20. Ces matrices engendrent des approximations de l’ image originale ci-dessous. On remarquera que l’ image originale correspond au cas r = 524. Impressionnant n’ est-ce pas?

Figure 8: cas r=1, 5, 10 et 20

Autres Utilisations

Les images numériques ont des applications dans de nombreux domaines: télédétection, transmission de données, médecine, robotique, vision par ordinateur, cinématographie, etc. En télédétection par exemple, les images obtenues par satellite sont utiles pour trouver des ressources naturelles, tracer des cartes et dans l’ étude de la croissance urbaine. Pour la transmission des images nous avons la communication par fax, réseaux, internet, et la télévision à circuit fermé pour la télésurveillance. Pour les utilisations médicales nous avons l’ utilisation des rayons X, la scanographie, la résonance magnétique et les ultrasons.

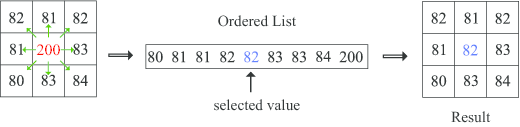
Certaines méthodes d’ acquisition et de transmission des images peuvent générer des parasites dans une image. Un filtre médian est une méthode de traitement utilisée pour supprimer les parasites ou réduire leurs effets: pour chaque élément d’ une matrice correspondant à une image, on observe les éléments de son voisinage et on arrange les éléments dans une liste ordonnée. Le filtre médian consiste à choisir l’ élément du centre de la liste et de le substituer à l’ élément central.

Figure 9: le principe du filtre médian

Figure 10: image avec le bruit et image avec le filtre médian

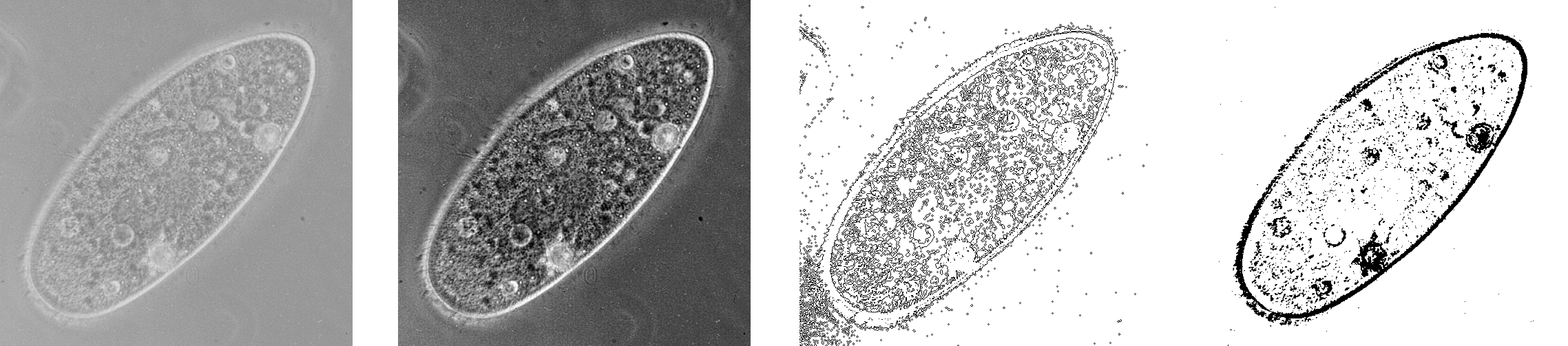
Il existe de nombreuses autres techniques de traitement de l’ image ayant différents objectifs. Les images ci-dessous illustrent un ajustement de contraste et une détection de contour.

Figure 11: image originale, ajustement de contraste, détection de contour et de seuil

Commentaire Final

Notre objectif avec ce texte est de présenter une application peu connue des matrices aux enseignants de lycées: le traitement des images numériques. Il est important de remarquer les outils mathématiques liés à ce sujet finissent par dépasser les matrices. Le sujet est vaste, riche et moderne. Malheureusement, la contrainte de quelques pages pour cette vignette ne nous permet pas de fournir plus de détails. Comme point de départ pour les lecteurs désireux d’en découvrir davantage, nous recommendons les ouvrages [Gonzalez et Woods, 2007] et [Gomes et Velho, 2008].

Références

Sur ce site internet site internet (ou son miroir), il y a une série d’ utilisations interactives qui vous permettront d’ explorer les relations entre les matrices et images numériques présentées dans ce texte. Un document DOC, qui propose divers exercices à utiliser en classe, est aussi disponible. Les images de Mona Lisa en LEGO sont la propriété de Marco Pece Udronotto, qui a aimablement autorisé leur utilisation dans cet article.

Voici les références citées dans le texte:

Gomes, J.; Velho, L. Image Processing for Computer Graphics and Vision. Springer-Verlag, 2008.

Gonzalez, R. C.; Woods, R. E. Digital Image Processing. Third Edition. Prentice Hall, 2007.

Lay, D. Linear Algebra and Its Applications. Forth Edition. Addison Wesley, 2011.

Poole, D. Linear Algebra: A Modern Introduction. Second Edition. Brooks Cole, 2005.

Les images de Mona Lisa en LEGO sont la propriété de Marco Pece Udronotto, qui a aimablement autorisé leur utilisation dans cet article.

Ce contenu a été publié dans Vignettes. Vous pouvez le mettre en favoris avec ce permalien.

Une réponse à Matrices et Images Numériques

  1. mailing dit :
    avril 16, 2014 à 8:44 am

    Très bel article, magnifique exposé, c’est très enrichissant, j’ai beaucoup appris. Je ne savais pas qu’il est possible de représenter ce type d’ image par des matrices. J’envisage informé un ami sur votre page. Trop génial!

    Répondre

Laisser un commentaire

Votre adresse e-mail ne sera pas publiée. Les champs obligatoires sont indiqués avec *