Cette image est la propriété de mathscareers.org.uk, qui a aimablement autorisé son utilisation pour cet article.
D’après le célèbre “théorème des quatre couleurs”, seulement quatre couleurs sont nécessaires pour colorier une carte sans que deux régions adjacentes aient la même couleur. En utilisant des équations polynomiales et les bases de Gröbner, nous pouvons déterminer si trois couleurs sont suffisantes pour colorier une carte donnée.
1. Coloration de carte
Le théorème des quatre couleurs (1) établit que n’importe quelle carte, qu’elle soit plane ou sphérique, peut être coloriée avec quatre couleurs sans que deux régions adjacentes soient de la même couleur. Il est facile de produire des exemples de cartes ne pouvant être coloriées avec seulement trois couleurs, et d’autre pouvant être coloriées avec trois couleurs. Une façon de déterminer si trois couleurs sont suffisantes pour colorier une carte consiste à analyser un système d’équations polynomiales associé à la carte. Chaque couleur est associée à une racine cubique (complexe) de l’unité et chaque région est symbolisée par une variable ![]() de sorte qu’elle ne peut qu’admettre l’une des trois valeurs, c’est-à-dire une des trois couleurs. Ainsi nous avons
de sorte qu’elle ne peut qu’admettre l’une des trois valeurs, c’est-à-dire une des trois couleurs. Ainsi nous avons ![]() pour chaque région.
pour chaque région.
Pour des régions ![]() et
et ![]() , nous avons
, nous avons ![]() . Si
. Si ![]() et
et ![]() sont des régions adjacentes, et puisque de telles régions ne peuvent pas être de la même couleur, alors
sont des régions adjacentes, et puisque de telles régions ne peuvent pas être de la même couleur, alors ![]() , c’est-à-dire,
, c’est-à-dire, ![]() . De cette façon, une carte avec
. De cette façon, une carte avec ![]() régions peut être coloriée avec trois couleurs si et seulement si le système d’équations polynomiales
régions peut être coloriée avec trois couleurs si et seulement si le système d’équations polynomiales
(1) ![]()
où ![]() et
et ![]() et
et ![]() représentent des régions adjacentes, admet au moins une solution.
représentent des régions adjacentes, admet au moins une solution.
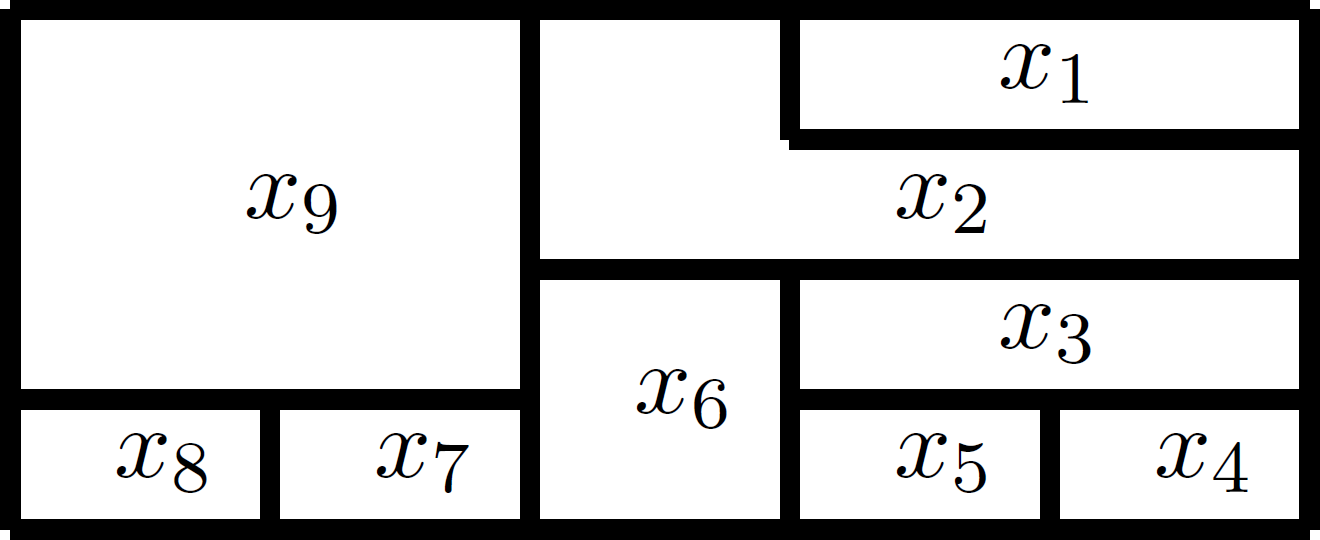
Exemple 1.
On considère la carte:
Peut-elle être coloriée avec trois couleurs?
Pour répondre à cette question on doit vérifier que le système polynomial 1 avec ![]() et
et
![]()
peut être résolu.
2. Systèmes d’équations polynomiales
La réponse à de nombreux problèmes de mathématiques réside dans la résolution de systèmes d’équations polynomiales, ce qui n’est pas toujours aisé. Si le système est donné par des équations linéaires, on peut, par la méthode du pivot de Gauss par exemple, substituer un système par un système équivalent dont la solution est plus facile à trouver. Dans le cas des systèmes polynomiaux, il existe une méthode analogue que nous présentons ci-dessous.
On notera ![]() l’ensemble des polynômes à coefficients complexes et à variables
l’ensemble des polynômes à coefficients complexes et à variables ![]() . Etant donné un ensemble de polynômes
. Etant donné un ensemble de polynômes ![]() dans
dans ![]() , on définit l’idéal qu’ils engendrent par
, on définit l’idéal qu’ils engendrent par
![]()
Un théorème du mathématicien David Hilbert: ![]() admet une solution (complexe) si et seulement si
admet une solution (complexe) si et seulement si ![]() . Comment peut-on vérifier la dernière condition?
. Comment peut-on vérifier la dernière condition?
Il est facile de vérifier que deux systèmes d’équations ![]() et
et ![]() , où
, où ![]() , vérifiant la condition
, vérifiant la condition
(2) ![]()
ont la même solution.
Par conséquent, la stratégie pour résoudre un système ![]() consiste à trouver des polynômes
consiste à trouver des polynômes ![]() satisfaisant la condition 2 et avec lesquels il est possible de vérifier si un élément
satisfaisant la condition 2 et avec lesquels il est possible de vérifier si un élément ![]() appartient ou non à l’idéal
appartient ou non à l’idéal ![]() et dont la solution commune est plus facile à calculer qu’avec le système d’origine.
et dont la solution commune est plus facile à calculer qu’avec le système d’origine.
L’existence théorique d’un tel ensemble ![]() a été découverte durant la première moitié du siècle dernier par le mathématicien Wolfgang Gröbner. Des années plus tard, son étudiant Bruno Buchberger créa un algorithme pour le calculer. Ces ensembles sont appelés bases de Gröbner et l’algorithme de Buchberger pour les calculer est un des outils de calcul algébrique les plus importants.
a été découverte durant la première moitié du siècle dernier par le mathématicien Wolfgang Gröbner. Des années plus tard, son étudiant Bruno Buchberger créa un algorithme pour le calculer. Ces ensembles sont appelés bases de Gröbner et l’algorithme de Buchberger pour les calculer est un des outils de calcul algébrique les plus importants.
Si l’idéal est de la forme ![]() , on a
, on a ![]() si et seulement si
si et seulement si ![]() , c’est-à-dire
, c’est-à-dire ![]() est divisible par
est divisible par ![]() . De même,
. De même, ![]() si et seulement si
si et seulement si ![]() , ce qui suggère quelque chose de similaire pour la division de
, ce qui suggère quelque chose de similaire pour la division de ![]() par
par ![]() . En fait, on peut diviser un polynôme à plusieurs variables par un ensemble fini de polynômes, à condition que les monômes soient ordonnés d’une certaine façon.
. En fait, on peut diviser un polynôme à plusieurs variables par un ensemble fini de polynômes, à condition que les monômes soient ordonnés d’une certaine façon.
3. Les Bases de Gröbner
Un monôme ![]() de
de ![]() est un élément de la forme
est un élément de la forme ![]() , où
, où ![]() sont des entiers positifs ou nuls. Le monôme
sont des entiers positifs ou nuls. Le monôme ![]() sera noté
sera noté ![]() . Parmi les ordres
. Parmi les ordres ![]() sur les monômes de
sur les monômes de ![]() , ceux qui satisfont
, ceux qui satisfont ![]() and
and ![]() lorsque
lorsque ![]() sont ceux qui rendent possible la mise en pratique de l’algorithme de division.
sont ceux qui rendent possible la mise en pratique de l’algorithme de division.
Un exemple est l’ordre lexicographique ![]() , où
, où ![]() , s’il existe
, s’il existe ![]() de sorte que
de sorte que ![]() et
et ![]() pour tous
pour tous ![]() .
.
Etant donné un ordre sur les monômes, le plus grand monôme d’un polynôme ![]() est appelé terme dominant de
est appelé terme dominant de ![]() et noté
et noté ![]() (pour “leading term”).
(pour “leading term”).
Une base de Gröbner d’un idéal ![]() relativement à un ordre sur les monômes, est, par définition, un ensemble
relativement à un ordre sur les monômes, est, par définition, un ensemble ![]() d’éléments de
d’éléments de ![]() de sorte que le terme dominant de chaque élément de
de sorte que le terme dominant de chaque élément de ![]() soit divisible par le terme dominant d’un élément de
soit divisible par le terme dominant d’un élément de ![]() . On peut montrer que chaque base de Gröbner
. On peut montrer que chaque base de Gröbner ![]() de
de ![]() est un ensemble qui vérifie la condition 2.
est un ensemble qui vérifie la condition 2.
Par conséquent, ![]() si et seulement si il existe une base de Gröbner de
si et seulement si il existe une base de Gröbner de ![]() contenant une constante non nulle, puisque
contenant une constante non nulle, puisque ![]() , pour chaque monôme
, pour chaque monôme ![]() de
de ![]() .
.
Par exemple, ![]() est une base de Gröbner de
est une base de Gröbner de ![]() , pour tout ordre sur les monômes, alors que
, pour tout ordre sur les monômes, alors que ![]() n’est pas une base de Gröbner de
n’est pas une base de Gröbner de ![]() pour l’ordre lexicographique, puisque
pour l’ordre lexicographique, puisque ![]() n’est pas divisible par
n’est pas divisible par ![]() .
.
Pour obtenir une base de Gröbner d’un idéal, pour un ordre sur les monômes donné, on peut utiliser l’algorithme de Buchberger (3). On trouve des algorithmes permettant de calculer des bases de Gröbner dans la majorité des systèmes de calcul algébrique.
En l’occurence, une base de Gröbner de l’idéal ![]() , pour l’ordre lexicographique, est
, pour l’ordre lexicographique, est ![]() .
.
4. Solution du problème et autres applications
Le système de l’exemple 1, a au plus un nombre fini de solutions (neuf variables, chacune pouvant prendre une valeur parmi trois). Le problème est de déterminer si le système admet une solution, et dans ce cas de la déterminer.
En appliquant l’algorithme de Buchberger au système de l’exemple 1, on obtient la base de Gröbner ![]() suivante, pour l’ordre lexicographique:
suivante, pour l’ordre lexicographique:
![]()
Ainsi, ![]() et par conséquent le système admet des solutions. Les équations
et par conséquent le système admet des solutions. Les équations
![Rendered by QuickLaTeX.com \[\left\{ \begin{array}{l} x_1 ^3 - 1 = 0 ~,\\ x_2 ^2 + x_2 x_1 + x_1 ^2 = 0 ~,\\ x_5 - x_2 = 0 ~,\\ x_7 - x_2 = 0 ~,\\ x_9 -x_3 = 0 ~, \end{array}\right.\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-36f8bc8d4e7db2b5289eac203cfe3381_l3.png)
traduisent le fait suivant: on peut utiliser n’importe quelle couleur pour ![]() ,
, ![]() ,
, ![]() et
et ![]() .
.
Puisque les couleurs sont représentées par des racines cubiques complexes de l’unité, la seule solution pour ![]() ,
, ![]() et
et ![]() est d’attribuer des valeurs (couleurs) distinctes pour
est d’attribuer des valeurs (couleurs) distinctes pour ![]() ,
, ![]() et
et ![]() , et donc
, et donc ![]() . Enfin,
. Enfin, ![]() qui nous donne deux possibilités:
qui nous donne deux possibilités: ![]() ou
ou ![]() , c’est-à-dire
, c’est-à-dire ![]() ,
, ![]() et
et ![]() ont des couleurs distinctes ou
ont des couleurs distinctes ou ![]() . Ainsi, on trouve, à une permutation des couleurs près, toutes les solutions possibles:
. Ainsi, on trouve, à une permutation des couleurs près, toutes les solutions possibles:
Les bases de Gröbner peuvent aussi être utilisées pour déterminer des idéaux, en convertisssant des équations paramétriques en équations cartésiennes (pour des surfaces et des courbes par exemples), pour calculer des polynômes minimaux de nombres algébriques, pour vérifier des théorèmes de géométrie Euclidienne, pour valider des constructions en origami et résoudre des grilles de sudoku (voir (4), (5) et (6)).
Références
(1) http://www.ipv.pt/millenium/Millenium24/12.pdf
(2) http://www.mat.uniroma1.it/people/manetti/dispense/nullstellen.pdf
(3) https://www.risc.jku.at/people/buchberg/papers/1970-00-00-A.english.pdf
(4) Adams, W. and Loustaunau, P., An Introduction to Gröbner Basis, AMS, Providence RI (1994).
(5) Cox, D; Little, J. and O’Shea, D., Ideals, Varieties and Algorithms, 2nd edition, Springer-Verlag, New York, (1996).
(6) Hernandes, M. E., Um Primeiro Contato com Bases de Gröbner, 28°. Colóquio Brasileiro de Matemática, IMPA, Rio de Janeiro, (2011).
Ce post est disponible en: Anglais, Allemand, Italien, Arabe, Khmère


 Français
Français 简体中文
简体中文  English
English  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português