Autor original: Christiane Rousseau.
Autor original: Christiane Rousseau.
En esta viñeta mostramos cómo descubrir, comenzando con un pequeño juego, uno de los teoremas más potentes de las matemáticas: el teorema del punto fijo de Banach. Este teorema tiene fantásticas aplicaciones tanto dentro como fuera de las matemáticas. En la sección 3 discutiremos su fascinante aplicación a la compresión de imágenes.
Pero comencemos con nuestro juego y echemos una mirada a la famosa tapa de una caja de La vaca que ríe.
El pendiente derecho de la vaca es de nuevo una tapa de La vaca que ríe. Asociamos a cada punto de la tapa el correspondiente punto del pendiente derecho. Por supuesto, esto define una función de la tapa en sí misma que llamaremos ![]() . Por ejemplo, a la punta de la barbilla de la vaca le asociamos la punta de la barbilla de la vaca pequeña en el pendiente derecho, al centro del ojo derecho de la vaca le asociamos el centro del ojo derecho de la vca pequeña en el pendiente derecho, etc. Aquí va la pregunta: ¿hay algún punto que sea enviado a sí mismo en este proceso? Un tal punto, si existe, se denomina punto fijo. Si existe un punto fijo entonces no es ninguno de los que hemos mencionado antes y, además, deberá estar en el pendiente derecho. Pero este pendiente derecho es enviado al pendiente derecho de la vaca pequeña, etc. Visualmente podemos imaginar que estos pendientes derechos anidados convergen a un punto que llamaremos
. Por ejemplo, a la punta de la barbilla de la vaca le asociamos la punta de la barbilla de la vaca pequeña en el pendiente derecho, al centro del ojo derecho de la vaca le asociamos el centro del ojo derecho de la vca pequeña en el pendiente derecho, etc. Aquí va la pregunta: ¿hay algún punto que sea enviado a sí mismo en este proceso? Un tal punto, si existe, se denomina punto fijo. Si existe un punto fijo entonces no es ninguno de los que hemos mencionado antes y, además, deberá estar en el pendiente derecho. Pero este pendiente derecho es enviado al pendiente derecho de la vaca pequeña, etc. Visualmente podemos imaginar que estos pendientes derechos anidados convergen a un punto que llamaremos ![]() y que este punto
y que este punto ![]() es un candidato a solución de nuestra pregunta.
es un candidato a solución de nuestra pregunta.
Ahora comencemos desde cualquier punto, por ejemplo la punta de la barbilla y llamémoslo ![]() . Entonces
. Entonces ![]() es enviado a
es enviado a ![]() , que es la punta de la barbilla de la vaca pequeña en el pendiente derecho;
, que es la punta de la barbilla de la vaca pequeña en el pendiente derecho; ![]() es enviado a
es enviado a ![]() , que es la punta de la barbilla de la vaca pequeña que aparece en el pendiente derecho, etc. Se observan tres cosas:
, que es la punta de la barbilla de la vaca pequeña que aparece en el pendiente derecho, etc. Se observan tres cosas:
- podemos continuar con el proceso un número infinito de veces y generar una sucesión
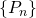 , donde
, donde 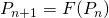 .
.
- Visualmente solo un número finito de puntos se la sucesión parecen diferentes, todos los demás no se pueden distinguir. Por supuesto, podemos hacer zoom y veremos más puntos, pero con cualquier zoom que elijamos solo diferenciaremos un número finito de puntos, los demás seguirán siendo indistinguibles.
- Esta sucesión parece converger al mismo punto
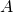 de antes.
de antes.
Si hubiéramos tomado otro punto ![]() y construido la sucesión
y construido la sucesión ![]() , donde
, donde ![]() , habríamos visto que la sucesión
, habríamos visto que la sucesión ![]() parecería converger al mismo punto
parecería converger al mismo punto ![]() . De hecho, esto de deduce del hecho de que el conjunto unipuntual
. De hecho, esto de deduce del hecho de que el conjunto unipuntual ![]() es la intersección de los pendientes derechos cuyo diámetro tiende a
es la intersección de los pendientes derechos cuyo diámetro tiende a ![]() .
.
¿Qué nos dice el teorema del punto fijo de Banach? Que la función ![]() tiene un único punto fijo, es decir, que existe un único punto
tiene un único punto fijo, es decir, que existe un único punto ![]() del plano tal que
del plano tal que ![]() . Más aún, nos dice que si tomamos cualquier punto
. Más aún, nos dice que si tomamos cualquier punto ![]() , la sucesión
, la sucesión ![]() , donde
, donde ![]() , converge a
, converge a ![]() .
.
Pero, ¿por qué? ¿Habría ocurrido esto para cualquier función ![]() ? Por supuesto que no. Por ejemplo, una traslación en el plano no tiene puntos fijos. Y La función
? Por supuesto que no. Por ejemplo, una traslación en el plano no tiene puntos fijos. Y La función ![]() tiene dos puntos fijos
tiene dos puntos fijos ![]() . La función
. La función ![]() de nuestro juego tiene una propiedad especial: es una contracción. De hecho, su imagen es mucho más pequeña que el dominio. Si dos puntos
de nuestro juego tiene una propiedad especial: es una contracción. De hecho, su imagen es mucho más pequeña que el dominio. Si dos puntos ![]() y
y ![]() están a cierta distancia, sus imágenes
están a cierta distancia, sus imágenes ![]() y
y ![]() están más cerca de lo que están
están más cerca de lo que están ![]() y
y ![]() . Esto tiene sentido porque en
. Esto tiene sentido porque en ![]() podemos medir la distancia entre dos elementos, ya que
podemos medir la distancia entre dos elementos, ya que ![]() es un espacio métrico. La propiedad contractiva de
es un espacio métrico. La propiedad contractiva de ![]() hace que cuando construimos la sucesión
hace que cuando construimos la sucesión ![]() no importe la precisión que tomemos (ya sea mirando la sucesión desde lejos, o acercándonos, o a través de un microscopio, o a través incluso de un microscopio electrónico), ya que después de cierto
no importe la precisión que tomemos (ya sea mirando la sucesión desde lejos, o acercándonos, o a través de un microscopio, o a través incluso de un microscopio electrónico), ya que después de cierto ![]() , que depende de la precisión elegida, todos los elementos
, que depende de la precisión elegida, todos los elementos ![]() ,
, ![]() , de la sucesión resultan indistinguibles. Dos elementos son distinguibles si la distancia entre ellos es mayor que cierta precisión. Veremos en la próxima sección que una sucesión con esta propiedad se llama sucesión de Cauchy. En
, de la sucesión resultan indistinguibles. Dos elementos son distinguibles si la distancia entre ellos es mayor que cierta precisión. Veremos en la próxima sección que una sucesión con esta propiedad se llama sucesión de Cauchy. En ![]() se tiene la propiedad de que toda sucesión de Cauchy tiene límite, por lo que decimos que
se tiene la propiedad de que toda sucesión de Cauchy tiene límite, por lo que decimos que ![]() es un espacio métrico completo.
es un espacio métrico completo.
1. El teorema del punto fijo de Banach
Tenemos ya todos los ingredientes necesarios para enunciar el teorema en el caso general.
Teorema (teorema del punto fijo de Banach). Sea ![]() un espacio métrico completo en el cual se denota por
un espacio métrico completo en el cual se denota por ![]() la distancia entre dos puntos
la distancia entre dos puntos ![]() y
y ![]() y sea
y sea ![]() una contracción, i.e. existe
una contracción, i.e. existe ![]() tal que para cualesquiera
tal que para cualesquiera ![]() se tiene que
se tiene que
![]()
Entonces ![]() tiene un único punto fijo, i.e. existe un único
tiene un único punto fijo, i.e. existe un único ![]() tal que
tal que ![]() .
.
Definimos ahora algunos de los términos que aparecen en el enunciado de este teorema. Esta parte es más formal y puede ser omitida si el lector prefiere concentrarse en las fascinantes aplicaciones del teorema.
Sabemos lo que es la distancia entre dos puntos ![]() y
y ![]() de
de ![]() . ¿Cómo lo generalizamos a un conjunto cualquiera
. ¿Cómo lo generalizamos a un conjunto cualquiera ![]() ?
?
Definición. Una distancia en un conjunto ![]() es una función
es una función ![]() que verifica
que verifica
- PAra cualesquiera
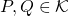 ,
, 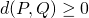 ;
;
-
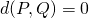 si y solo si
si y solo si 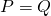 ;
;
- Para cualesquiera
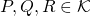 ,
, 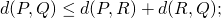 (desigualdad triangular.)
(desigualdad triangular.)
Es conocido que la distancia euclídea usual en ![]() verifica estas propiedades.
verifica estas propiedades.
Recordamos ahora la definición de sucesión de Cauchy, que es una formalización de la idea de uan sucesión para la cual todos los elementos posteriores a un número finito de ellos son indistinguibles, sea cual sea la preción elegida. También presentamos la definición de sucesión convergente.
Definición.
- Una sucesión
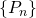 de elementos de un espacio métrico
de elementos de un espacio métrico 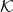 es una sucesión de Cauchy si para todo
es una sucesión de Cauchy si para todo 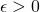 , existe
, existe 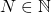 tal que para todos
tal que para todos 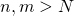 , se tiene que
, se tiene que
![Rendered by QuickLaTeX.com \[d(P_n,P_m)<\epsilon.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-1c97f4794c43d7a0ea39241b9d7b70f0_l3.png)
- Una sucesión
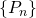 de elementos de un espacio métrico
de elementos de un espacio métrico 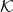 converge a un límite
converge a un límite 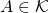 si para todo
si para todo 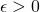 , existe
, existe 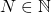 tal que para todo
tal que para todo 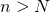 , se tiene que
, se tiene que
![Rendered by QuickLaTeX.com \[d(P_n,A)<\epsilon.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-15d19b7399d98032c767b201bb2322a3_l3.png)
Definición. Un espacio métrico ![]() es un espacio métrico completo si toda sucesión de Cauchy
es un espacio métrico completo si toda sucesión de Cauchy ![]() de elementos
de elementos ![]() converge a un elemento
converge a un elemento ![]() de
de ![]() .
.
¿Cómo se prueba el teorema del punto fijo de Banach? La unicidad del punto fijo es fácil: supongamos que ![]() y
y ![]() son dos puntos fijos. Se tiene que
son dos puntos fijos. Se tiene que ![]() y
y ![]() y como
y como ![]() es una contracción
es una contracción
![]()
y, por tanto, ![]() . La única solución es
. La única solución es ![]() , lo que nos da
, lo que nos da ![]() .
.
En cuanto a la existencia, la idea de la demostración es también sencilla y ya la hemos encontrado en nuestro juego de La vaca que ríe. Tomamos cualquier punto ![]() y construimos (como antes) la sucesión
y construimos (como antes) la sucesión ![]() , donde
, donde ![]() . Esta sucesión es de Cauchy y su límite es un punto fijo. (Por supuesto, probar estas dos afirmaciones requiere trabajo, pero omitimos los detalles técnicos; lo que es realmente importante es que la demostración es la misma en el caso general con un espacio métrico completo complicado que en el caso sencillo
. Esta sucesión es de Cauchy y su límite es un punto fijo. (Por supuesto, probar estas dos afirmaciones requiere trabajo, pero omitimos los detalles técnicos; lo que es realmente importante es que la demostración es la misma en el caso general con un espacio métrico completo complicado que en el caso sencillo ![]() .)
.)
La idea de la demostración no es solo sencilla e intuitiva, sino también muy potente: proporciona una manera de construir numéricamente el punto fijo ![]() . Esto explica las muchas aplicaciones de este teorema, que se pueden encontrar tanto en el aspecto teórico como en el aplicado.
. Esto explica las muchas aplicaciones de este teorema, que se pueden encontrar tanto en el aspecto teórico como en el aplicado.
2. Aplicaciones en análisis
Una de las aplicaciones teóricas más importantes del teorema del punto fijo de Banach es la demostración de la existencia y unicidad de soluciones de ecuaciones diferenciales suficientemente regulares. En este caso el espacio métrico completo ![]() es un conjunto de funciones y la función
es un conjunto de funciones y la función ![]() transforma una función en otra función (frecuentemente se dice que
transforma una función en otra función (frecuentemente se dice que ![]() es un operador). El truco es probar que si existe solución de la ecuación diferencial, esta es un punto fijo del operador
es un operador). El truco es probar que si existe solución de la ecuación diferencial, esta es un punto fijo del operador ![]() .
.
Probablemente el lector haya estudiado ecuaciones difereciales sencillas y aprendido trucos para hallar fórmulas para las soluciones. Estas ecuaciones diferenciales son una excepción: en la mayor parte de las ecuaciones diferenciales no existe ninguna fórmula para la solución, de ahí la importancia de un teorema que asegure la existencia de solución. La no existencia de fórmulas para expresar la solución de la mayor parte de las ecuaciones diferenciales no debería sorprender al lector. De hecho, si se considera la sencilla ecuación diferencial
![]()
su solución viene dada por
![]()
El lector recordará de sus cursos de probabilidad o estadística que no existe fórmula para la primitiva de la función ![]() , explicando así por qué se necesita trabajar con tablas cuando se estudia la distribución normal.
, explicando así por qué se necesita trabajar con tablas cuando se estudia la distribución normal.
3. Aplicación a la compresión de imágenes
La mejor manera de almacenar una imagen en memoria es almacenar el color de cada píxel. Este método presenta dos problemas:
- Requiera una enorme cantidad de memoria.
- Si se intenta ampliar la imagen, for ejemplo para usarla en un póster de mayor tamaño, entonces los píxeles serán cuadrados más grandes y faltará la información de cómo rellenar los detalles en esos cuadrados.
¿Cuál es el principio de la compresión de imágenes? Codificar una cantidad de información menor a la que supondría la imagen orginal pero en hacerlo de una manera inteligente, de manera que el ojo no pueda captar que la imagen observada está deteriorada. Internet ha aumentado la necesidad de una buena compresión de imágenes. De hecho, las imágenes ralentizan de modo significativo la navegación en la red.  Por tanto, para la navegación por internet es bueno tener las imágenes codificadas en archivos lo más pequeños posible. Cuando se mira una imagen en la pantalla de su ordenador no se percibe que la imagen ha sido deteriorada, pero si se trata de agrandarla o de usarla para un póster, entonces se ve que la calidad es pobre.
Por tanto, para la navegación por internet es bueno tener las imágenes codificadas en archivos lo más pequeños posible. Cuando se mira una imagen en la pantalla de su ordenador no se percibe que la imagen ha sido deteriorada, pero si se trata de agrandarla o de usarla para un póster, entonces se ve que la calidad es pobre.
Existen diversos principios de compresión de imágenes; uno de los más familiares es JPEG, que se ha convertido en el estándar para fotografías digitales. La codificación de una imagen en formato JPEG es también un algoritmo matemático.
 En esta viñeta nos centraremos en otro método, que ha permanecido más experimental. Este método, introducido por Barnsley, se denomina sistemas de funciones iteradas. La idea subyacente de este método es aproximar una imagen mediante objetos geométricos. Para tener suficientes objetos disponibles no nos limitamos a los objetos geométricos usuales, como son las líneas y las curvas suaves, sino que incluimos complejos objetos fractales como el helecho y la alfombra de Sierpiński (ver las figuras de la izquierda).
En esta viñeta nos centraremos en otro método, que ha permanecido más experimental. Este método, introducido por Barnsley, se denomina sistemas de funciones iteradas. La idea subyacente de este método es aproximar una imagen mediante objetos geométricos. Para tener suficientes objetos disponibles no nos limitamos a los objetos geométricos usuales, como son las líneas y las curvas suaves, sino que incluimos complejos objetos fractales como el helecho y la alfombra de Sierpiński (ver las figuras de la izquierda).
 Explicaremos la idea del proceso de compresión en la alfombra de Sierpiński de la izquierda, que a priori parece un objeto complicado. ¿Cómo almacenarlo en la memoria del ordenador de una manera «económica»? La mejor solución es almacenar un programa para reconstruirla cuando se necesite.
Explicaremos la idea del proceso de compresión en la alfombra de Sierpiński de la izquierda, que a priori parece un objeto complicado. ¿Cómo almacenarlo en la memoria del ordenador de una manera «económica»? La mejor solución es almacenar un programa para reconstruirla cuando se necesite.
Para contruir este programa se necesita comprender qué caracteriza a este objecto geométrico. Observemos la alfombra de Sierpiński: es la unión de tres alfombras de Sierpiński (es decir, 3 copias de sí misma), cuyas dimensiones (altura y anchura) son la mitad. De hecho, comenzando por la alfombra de Sierpiński podemos construir una segunda mediante el siguiente procedimiento:
- Se encoge la alfombra de Sierpiński a la mitad de sus dimensiones desde el vértice inferior izquierdo.
- Se hace una copia de esta segunda alfombra de Sierpiński y se pega a la derecha de ella.
- Se hace una última copia de la segunda alfombra de Sierpiński y se pega en la parte superior.
La figura que se ha construido es idéntica a la alfombra de Sierpiński inicial. Por tanto, la alfombra de Sierpiński es el punto fijo de este proceso.
Expresemos ahora todo esto en términos matemáticos. Notar que la longitud de la base de la alfombra de Sierpiński es igual a su altura. Por tanto, podemos tomar ejes coordenados con origen en la esquina inferior izquierda de la alfombra de Sierpiński y con unidades de manera que la base y la altura tengan ambas longitud 1. Consideramos también la siguiente transformación afín definida en ![]() :
:
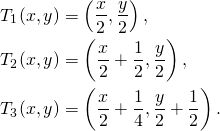
Si ![]() es la alfombra de Sierpiński entonces se tiene que
es la alfombra de Sierpiński entonces se tiene que
![]()
¿Existen otros subconjuntos ![]() del plano que tengan la misma propiedad, es decir,
del plano que tengan la misma propiedad, es decir,
(1) ![]()
Experimentaremos y comprobaremos que no. Por tanto, hemos caracterizado la alfombra de Sierpiński como el único subconjunto ![]() del plano que satisface (1) ¿Qué hemos hecho para ello? Hemos construido una función que a cada subconjunto
del plano que satisface (1) ¿Qué hemos hecho para ello? Hemos construido una función que a cada subconjunto ![]() del plano le asocia el subconjunto
del plano le asocia el subconjunto ![]() . Llamemos a esta función
. Llamemos a esta función ![]() . Está definida por
. Está definida por
(2) ![]()
y hemos observado que ![]() , i.e.
, i.e. ![]() es un punto fijo de esta función.
es un punto fijo de esta función.
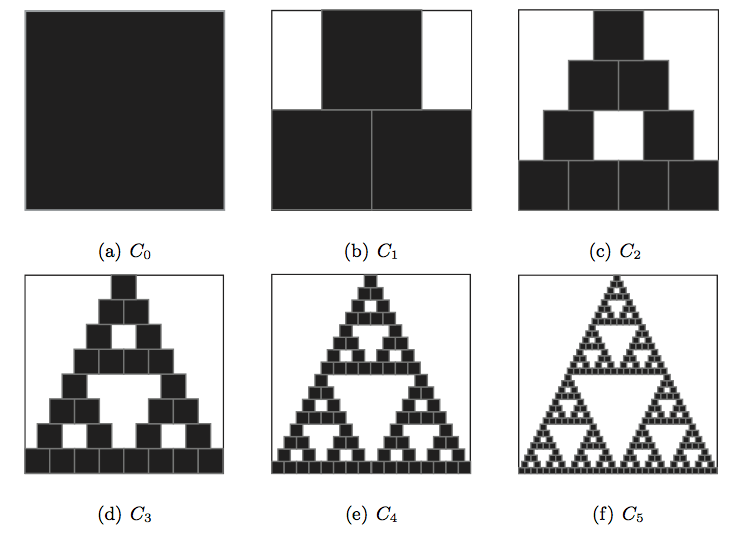
Hemos dicho que probaríamos que la alfombra de Sierpiński es el único punto fijo de esta función. Probemos con un cuadrado ![]() como en la Figura 1(a). Su imagen es
como en la Figura 1(a). Su imagen es ![]() en la Figura 1(b). Aplicamos el mismo proceso a
en la Figura 1(b). Aplicamos el mismo proceso a ![]() y obtenemos
y obtenemos ![]() ,
, ![]() –
–![]() . (Figura 1 (c)-(f)).
. (Figura 1 (c)-(f)).
Observamos tres hechos:
- Ninguno de los conjuntos
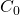 , …,
, …, 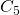 es un punto fijo de
es un punto fijo de 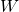 .
.
- Podríamos haber continuado el proceso indefinidamente produciendo la secuencia infinita de conjuntos
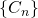 , donde
, donde 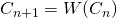 .
.
- La secuencia
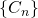 parece converger rápidamente a la alfombra de Sierpiński. De hecho, nuestro ojo no puede distinguir
parece converger rápidamente a la alfombra de Sierpiński. De hecho, nuestro ojo no puede distinguir 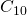 de
de  . Por tanto, el programa que reconstruyera nuestra imagen podría producir simplemente
. Por tanto, el programa que reconstruyera nuestra imagen podría producir simplemente 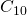 en lugar de
en lugar de  . Si necesitáramos una mejor resolución, entonces podríamos usar el mismo programa y hacerlo parar en
. Si necesitáramos una mejor resolución, entonces podríamos usar el mismo programa y hacerlo parar en 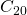 o
o 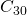 . Luego el mismo pequeño programa puede reconstruir
. Luego el mismo pequeño programa puede reconstruir  a cualquier preción.
a cualquier preción.
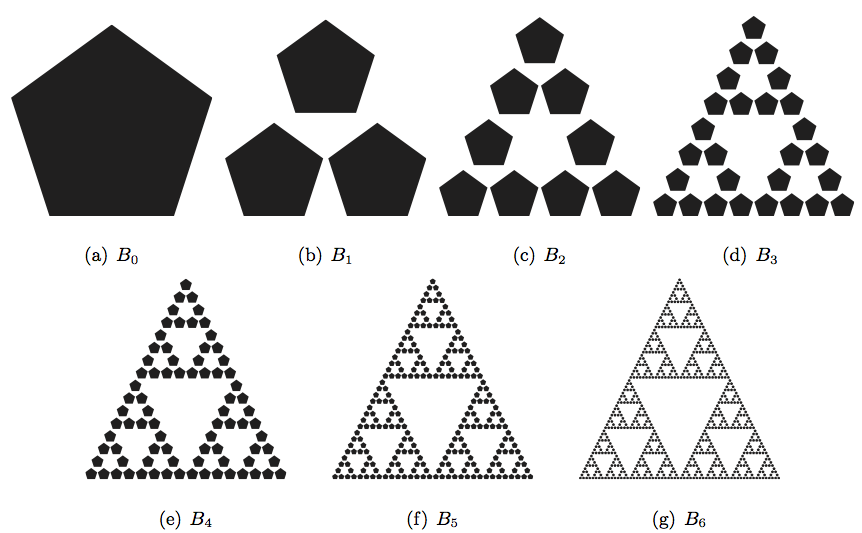
No solo eso: podemos comprobar que funciona con cualquir conjunto inicial que tomemos. Como segundo ejemplo iteremos el pentágono que aparece en la Figura 2. Las mismas observaciones (i), (ii) y (iii) anteriores se aplican también a este ejemplo.
Hemos visto que el teorema del punto fijo de Banach se aplica a contracciones en espacios métrico completos. Hemos definido la función ![]() (2) en subconjuntos del plano. Como espacio métrico tomaremos
(2) en subconjuntos del plano. Como espacio métrico tomaremos ![]() como el conjunto de los subconjuntos acotados (cerrados) del plano. Introducimos una distancia en
como el conjunto de los subconjuntos acotados (cerrados) del plano. Introducimos una distancia en ![]() llamada distancia de Hausdorff. La definición de distancia de Hausdorff
llamada distancia de Hausdorff. La definición de distancia de Hausdorff ![]() , entre dos subconjuntos
, entre dos subconjuntos ![]() y
y ![]() es una fórmula compicada y confusa, por lo que explicaremos el concepto de otra manera. Comencemos por explicar qué significado queremos darle a la expresión
es una fórmula compicada y confusa, por lo que explicaremos el concepto de otra manera. Comencemos por explicar qué significado queremos darle a la expresión
![]()
(incluso sin haber definido qué es ![]() ). Esto significará únicamente que si nuestro ojo tiene precisión
). Esto significará únicamente que si nuestro ojo tiene precisión ![]() , entonces no pouede distinguir
, entonces no pouede distinguir ![]() de
de ![]() . En términos matemáticos,
. En términos matemáticos, ![]() significaría
significaría
(3) ![]()
(Aquí ![]() es la distancia euclídea usual en
es la distancia euclídea usual en ![]() .) Esto permite dar la siguiente definición indirecta.
.) Esto permite dar la siguiente definición indirecta.
Definición. La distancia de Hausdorff entre dos conjuntos cerrados y acotados ![]() y
y ![]() es el mínimo de todos los
es el mínimo de todos los ![]() tales que se satisface (3).
tales que se satisface (3).
Ahora debemos convencernos de que la función ![]() es una contracción. Supongamos que
es una contracción. Supongamos que ![]() . Entonces podemos probar que
. Entonces podemos probar que ![]() . Sea
. Sea ![]() ; se tiene que existen
; se tiene que existen ![]() y
y ![]() tales que
tales que ![]() . Como
. Como ![]() , existe
, existe ![]() tal que
tal que ![]() . Sea
. Sea ![]() ; entonces
; entonces ![]() y
y ![]() . Análogamente, si comenzamos con
. Análogamente, si comenzamos con ![]() entonces existe
entonces existe ![]() tal que
tal que ![]() .
.
Este proceso se ha adaptado a la compresión de imágenes reales (ver [K] o [RS]). El método produce imágenes de lata calidad cuando la imagen tiene carácter fractal. Sin embargo, la tasa de compresión no es tan buena ni tan flexible como en el formato JPEG. El proceso de codificación (transformar la imagen en un programa para reconstruirla) resulta todavía demasiado tedioso como para ser de interés práctico. Sin embargo, la simplicidad de la idea junto con su potencia siguen siendo llamativas.
4. Una aplicación sorprendente: el algoritmo PageRank
El éxito de Google como motor de búsqueda proviene de su algoritmo: el algoritmo PageRank. En este algoritmo se calcula el punto fijo de un operador lineal en ![]() que es una contracción y cuyo punto fijo (que es un vector) produce la ordenación de las páginas. En la práctica, el punto fijo (que es un vector propio de valor propio
que es una contracción y cuyo punto fijo (que es un vector) produce la ordenación de las páginas. En la práctica, el punto fijo (que es un vector propio de valor propio ![]() ) se calcula aproximadamente como
) se calcula aproximadamente como ![]() para
para ![]() suficientemente grande. Invitamos al lector a leer los detalles en la viñeta Cómo funciona Google.
suficientemente grande. Invitamos al lector a leer los detalles en la viñeta Cómo funciona Google.
5. Conclusión
En esta viñeta hemos probado cómo comenzando con un simple juego podemos descubrir ideas muy potentes que pueden llevar a importantes avances matemáticos y tecnológicos. En muchos campos de las matemáticas cuando se busca solución única a un problema, se ha convertido en un método estándar tratar de probar que dicha solución se puede caracterizar como el único punto fijo de un operador especialmente construido para ese propósito.
Hemos visto que la ventaja de esta aproximación es que el teorema proporciona un método práctico y eficiente para construir el objeto solución como el límite de una sucesión, ya que la convergencia es rápida.
El análisis matemático consiste en estudiar funciones. Las funciones se definen habitualmente sobre números. En el cálculo en varias variables se generaliza la noción de funciones a vectores que son elementos de ![]() . ¿Por qué parar simplemente con elementos de
. ¿Por qué parar simplemente con elementos de ![]() ? Hemos visto que a los matemáticos les gusta generalizar la nocion de función y definirlas, por ejemplo, en conjuntos de conjuntos, en conjuntos de funciones, etc. Hacer análisis en conjuntos de funciones se ha convertido en un importante capítulo del análisis moderno, llamado análisis funcional, materia estándar en los estudios de grado.
? Hemos visto que a los matemáticos les gusta generalizar la nocion de función y definirlas, por ejemplo, en conjuntos de conjuntos, en conjuntos de funciones, etc. Hacer análisis en conjuntos de funciones se ha convertido en un importante capítulo del análisis moderno, llamado análisis funcional, materia estándar en los estudios de grado.
Se invita al lector a establecer el vínculo con cualquier otro proceso iterativo que conozca. Por ejemplo, el proceso iterativo en dimensión 1 asociado a la sucesión de Herón para hallar raíces cuadradas. La rápida convergencia geométrica se puede entender también desde el punto de vista presentado aquí.
Bibliografía
[B] M. F. Barnsley, Fractals everywhere, San Diego, Academic Press, 1988.
[K] J. Kominek, Advances in fractal compression for
multimedia applications, Multimedia Systems Journal, vol. 5,
n![]() 4, 1997, 255–270.
4, 1997, 255–270.
[R] C. Rousseau, Point fixe de Banach (in French), Accromath 5, hiver-printemps 2010 (www.accromath.ca).
[R2] C. Rousseau, How Google works? Klein vignette (www.kleinproject.org).
[RS] C. Rousseau and Y. Saint-Aubin, Mathematics and
technology, SUMAT Series, Springer-Verlag, 2008 (A French version of the book, Mathéematiques et technologie, exists, published in the same series.)