
 Autor original: Christiane Rousseau.
Autor original: Christiane Rousseau.
¿Cómo se mide el tamaño de un objeto geométrico? Para subconjuntos del plano habitualmente se usan el perímetro, al longitud, el área, el díametro, etc. Pero esto no es suficiente para describir los fractales. Los fractales son objetos geométricos muy complejos y deberíamos tener una manera de medir esa complejidad. Con este fin los matemáticos han introducido el concepto de dimensión. El concepto de dimensión proporciona una medida de la complejidad de un fractal. La noción de dimensión es una generalización y una formalización de nuestra idea intuitiva de dimensión cuando hablamos de 1D, 2D o 3D. En esta viñeta discutiremos varioas maneras de describir objetos fractales a trevés de dos ejemplos: la alfombra de Sierpinski y el copo de nieve de von Koch (ver figuras a la izquierda).
¿Cuál es el área de la alfombra de Sierpinski
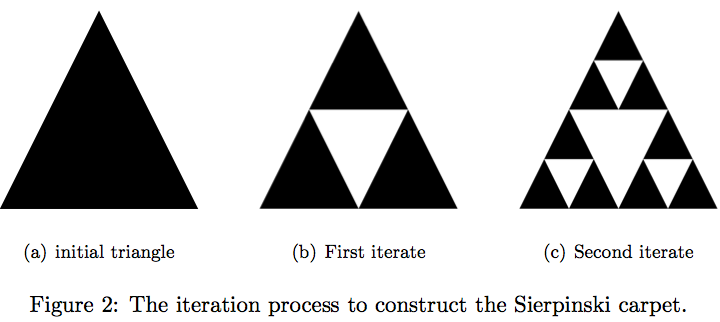
Primero necesitamos conprender la construcción de la alfombra de Sierpinski (ver Figura 2). Está hecha mediante un proceso iterativo. Comenzamos con un triángulo y eliminamos el triángulo central, quedándonos con tres triángulos. En cada uno de estos triángulos tenemos que eliminar el triángulo central y así sucesivamente.
Ahora tenemos todos los ingredientes necesarios para calcular el área de la alfombra de Sierpinski. Supongamos que el triángulo inicial (ver Figura2(a)) es ![]() .
.
- En la primera iteración eliminamos un áerea de
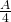 y nos quedamos con un área de
y nos quedamos con un área de 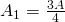 .
.
- En la segunda iteración eliminamos un cuarto del área de los triángulos restantes, luego un cuarto de
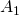 . Por tanto, el área que queda es
. Por tanto, el área que queda es 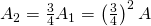 .
.
- En la tercera iteración eliminamos un cuarto del área de los nueve triángulos restantes, luego un cuarto de
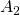 . Por tanto, el a´rea restante es
. Por tanto, el a´rea restante es 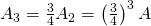 .
.
- …
- En la
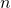 -ésima iteración, eliminamos un cuarto del área de los
-ésima iteración, eliminamos un cuarto del área de los 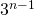 triángulos restantes, luego un cuarto de
triángulos restantes, luego un cuarto de 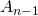 . Por tanto, el área restante es
. Por tanto, el área restante es 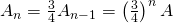 .
.
- …
Como
![]()
podemos concluir que el área de la alfombra de Sierpinski es cero.
¿Cuál es la longitud del copo de nieve de von Koch?
El copo de nieve de von Koch se obtiene también por iteración. En cada paso de la iteración reemplazamos cada segmento por un grupo de 4 segmentos, cada uno de ellos igual a ![]() de la longitud del segmento original (ver Figura 3). Si
de la longitud del segmento original (ver Figura 3). Si ![]() es la longitud del triángulo original en la Figura 3(a), entonces
es la longitud del triángulo original en la Figura 3(a), entonces ![]() es la longitud de la estrella de la Figura 3(b),
es la longitud de la estrella de la Figura 3(b), ![]() es la longitud del objeto en la Figura 3(c), etc. En particular, esto significa que, en cada paso, la longitud se multiplica por
es la longitud del objeto en la Figura 3(c), etc. En particular, esto significa que, en cada paso, la longitud se multiplica por ![]() . Como en la construcción hay un número infinito de pasos, la longitud del copo de nieve de von Koch es infinita.
. Como en la construcción hay un número infinito de pasos, la longitud del copo de nieve de von Koch es infinita.
La alfombra de Sierpinski es un objeto muy complejo. Sin embargo, su área es cero y, por tanto, nos da poca información acerca de él. El hecho de que la longitud del copo de nieve de von Koch sea infinita nos dice que el objeto es muy complejo, pero sin más precisión. Para ser capaces de dar más información acerca de objetos fractales, los matemáticos introdujeron el concepto de dimensión.
Si comenzamos con nuestra idea intuitiva de dimensión, las curvas suaves tiene dimesnión ![]() , las superficies suaves tienen dimensión
, las superficies suaves tienen dimensión ![]() y los volúmenes rellenos tienen dimensión
y los volúmenes rellenos tienen dimensión ![]() . Por tanto, deberemos dar una definición matemática de dimensión que sea
. Por tanto, deberemos dar una definición matemática de dimensión que sea ![]() para curvas suaves,
para curvas suaves, ![]() para superficies suaves y
para superficies suaves y ![]() para volúmenes rellenos. En esta viñeta nos restringiremos solo a dimensiones
para volúmenes rellenos. En esta viñeta nos restringiremos solo a dimensiones ![]() y
y ![]() . Queremos cubrir un objeto geométrico en el plano con pequeños cuadrados. (Si quisiéramos definir dimensión
. Queremos cubrir un objeto geométrico en el plano con pequeños cuadrados. (Si quisiéramos definir dimensión ![]() , usaríamos pequeños cubos, pero podríamos haber usado cubos para curvas y superficies sin cambiar la dimensión.
, usaríamos pequeños cubos, pero podríamos haber usado cubos para curvas y superficies sin cambiar la dimensión.
El caso de una curva suave. (ver Figura 4)
- si tomamos cuadrados de lado la mitad, necesitaremos aproximadamente el doble de cuadrados para cubrir el objeto;
- Si tomamos cuadrados de lado un tercio, necesitaremos aproximadamente tres veces más cuadrados para cubrir el objeto;
- …
- Si tomamos cuadrados de lado
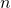 veces menor, necesitaremos aproximadamente
veces menor, necesitaremos aproximadamente 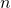 veces más cuadrados para cubrir el objeto;
veces más cuadrados para cubrir el objeto;
El caso de una superficie suave. (ver Figura 5)
- si tomamos cuadrados de lado la mitad, necesitaremos aproximadamente cuatro veces más cuadrados para cubrir el objeto;
- Si tomamos cuadrados de lado un tercio, necesitaremos aproximadamente nueve veces más cuadrados para cubrir el objeto;
- …
- si tomamos cuadrados de lado
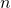 veces menor, necesitaremos aproximadamente
veces menor, necesitaremos aproximadamente 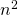 veces más cuadrados para cubrir el objeto;
veces más cuadrados para cubrir el objeto;
Ahora podemos dar la definición (intuitiva) de dimensión:
Definición. Un objeto en el plano tiene dimensión ![]() si cuando tomamos cuadrados de lado
si cuando tomamos cuadrados de lado ![]() veces menor para cubrirlo, necesitamos aproximadamente
veces menor para cubrirlo, necesitamos aproximadamente ![]() cuadrados más para cubrirlo.
cuadrados más para cubrirlo.
Algunas observaciones a la definición.
- Los cuadrados que hemos utilizado para cubrir el objeto pueden estar girados o pueden superponerse.
- En lugar de ucadrados podríamos haber itulizado rectángulos del mismo tamaño con un ratio
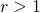 entre la longitud y la anchura. Habríamos obtenido los mismos resultados para dimensiones
entre la longitud y la anchura. Habríamos obtenido los mismos resultados para dimensiones  y
y 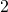 . Este es, de hecho, el caso general en dimensión
. Este es, de hecho, el caso general en dimensión 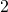 . Para calcular la dimensión del copo de nieve de Koch es más fácil usar resctángulos que cuadrados.
. Para calcular la dimensión del copo de nieve de Koch es más fácil usar resctángulos que cuadrados.
Esta definición puede ser generalizada a objetos geométricos que sean subconjuntos de ![]() y el resultado no depende del
y el resultado no depende del ![]() que consideremos.
que consideremos.
Definición. Un subconjunto de ![]() tiene dimensión
tiene dimensión ![]() if, si cuando tomamos hipercubos
if, si cuando tomamos hipercubos ![]() -dimensional de lado
-dimensional de lado ![]() veces menor para cubrirlo, entonces se necesitan aproximadamente
veces menor para cubrirlo, entonces se necesitan aproximadamente ![]() más hipercubos para cubrirlo.
más hipercubos para cubrirlo.
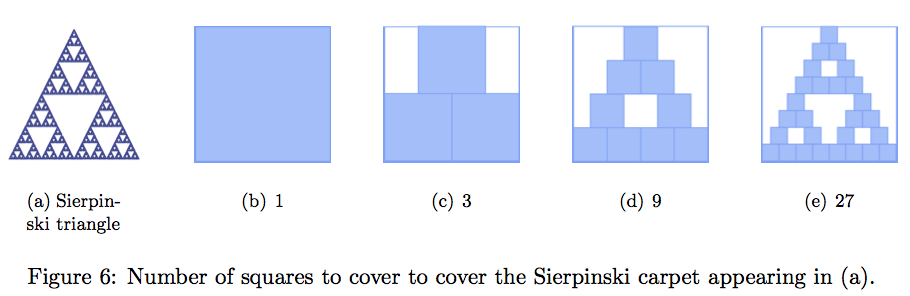
No todos los objetos tienen dimensión. Los objetos autosimilares tienen una dimensión que, en la mayor parte de los casos, no es un número entero. Calculemos la dimensión de la alfombra de Sierpinski (ver Figura 6).
- Si tomamos un cuadrado de lado igual a la longitud de la base, este cuadrado cubre la alfombra de Sierpinski de la Figura 6(a).
- Si tomamos cuadrados de lado la mitad, necesitaremos 3 cuadrados para cubrir la alfombra. Notar que
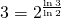 (Figura 6(c)).
(Figura 6(c)).
- Si tomamos cuadrados de lado un cuarto, necesitaremos 9 cuadrados para cubrir la alfombra. Notar que
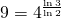 (Figura 6(d)).
(Figura 6(d)).
- Si tomamos cuadrados de lado un octavo, necesitaremos
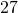 cuadrados para cubrir la alfombra. Notar que
cuadrados para cubrir la alfombra. Notar que 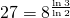 (Figure 6(e)).
(Figure 6(e)).
Por tanto, es fácil concluir que el triángulo de Sierpinski de la Figura 6(a) es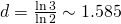 .
.
Aseguramos que la dimensión del copo de nieve de Koch de la Figura 3(b) es
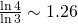 . ¿Por qué? Si tratamos de cubrirlo con cuadrados que tengan como lado la longitud del lado de la siguiente iteración, como en la Figura 4, la primera dificultad que aparece es el hecho de que algunos cuadrados cubren un únicamente parte de un lado y otros pueden cubrir parte de dos, cuando estos se encuentran formando un pico. Por tanto, usemos el truco del que hemos hablado en nuestra segunda observación y usemos rectángulos de longitud
. ¿Por qué? Si tratamos de cubrirlo con cuadrados que tengan como lado la longitud del lado de la siguiente iteración, como en la Figura 4, la primera dificultad que aparece es el hecho de que algunos cuadrados cubren un únicamente parte de un lado y otros pueden cubrir parte de dos, cuando estos se encuentran formando un pico. Por tanto, usemos el truco del que hemos hablado en nuestra segunda observación y usemos rectángulos de longitud 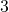 veces la anchura. Explicaremos únicamente los pasos principales del razonamiento, dejando los detalles al lector. En cada iteración usamos tantos rectángulos como lados tiene la figura y cuya longitud es la longitud del lado de dicha figura. Si colocamos los rectángulos en la parte exterior del copo de von Koch entonces cubrirán los nuevos picos que se añadan en las siguientes iteraciones. Es fácil comprobar que se necesitan tantos rectángulos como número de lados. En el triángulo inicial se tienen tres lados y, al pasar de una iteración a la siguiente el número de lados se multiplica por
veces la anchura. Explicaremos únicamente los pasos principales del razonamiento, dejando los detalles al lector. En cada iteración usamos tantos rectángulos como lados tiene la figura y cuya longitud es la longitud del lado de dicha figura. Si colocamos los rectángulos en la parte exterior del copo de von Koch entonces cubrirán los nuevos picos que se añadan en las siguientes iteraciones. Es fácil comprobar que se necesitan tantos rectángulos como número de lados. En el triángulo inicial se tienen tres lados y, al pasar de una iteración a la siguiente el número de lados se multiplica por 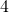 , luego el número de rectángulos también se multiplica por
, luego el número de rectángulos también se multiplica por 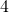 y estos rectángulos tienen sus lados
y estos rectángulos tienen sus lados 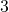 veces menores que los de la iteración anterior. Como
veces menores que los de la iteración anterior. Como 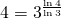 , concluimos que la dimensión del copo de nieve de von Koch es
, concluimos que la dimensión del copo de nieve de von Koch es 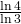 .
. La dimensión da una “medida” de la complejidad o densidad de un fractal. De hecho, se intuye que la alfombra de Sierpinski es más densa que el copo de nieve de von Koch, que parece más una curva engrosada. Esto se ve reflejado en el hecho de que
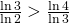 .
. Aplicaciones
La red capilar alrededor de un tumor. no es igual que en el resto del cuerpo. Este hecho se está investigando (en particular, su dimensión fractal), para mejorar en el diagnóstico utilizando imágenesmédicas.
El diseño del árbol bronquial. Los atletas de alto nivel tienen mayor probabilidad de sufrir asma que el resto de la población. ¿Por qué? En el artículo [Ma] se estudia el pulmón “óptimo”. Hay 17 niveles de tubos bronquiales antes de llegar a los bronquiolos y acinos involucrados en el intercambio de aire. Si los tubos bronquiales son demasiado estrechos entonces la presión aumenta cuando el aire penetra en el siguiente nivel de tubos bronquiales. Pero si son demasaido anchos, entonces el volumen permanece constante en cada nivel y se hace demasiado grande (sería infinito si tuviera infirnitos niveles). Por tanto, el pulmón “óptimo” debería tener el mínimo volumen que sea posible sin aumentar la presión. Sin embargo, cerca del pulmón óptimo, una pequeña disminución en el diámetro de los tubos bronquiales conlleva un mayor incremento de la presión que la misma disminución en tubos bronquiales más anchos (esto proviene de la forma no lineal especial de la función que da la presión). Los pulmones humanos tienen los tubos bronquiales más anchos y un mayor volumen que el teórico pulmón óptimo. Esta diferencia proporciona protección en caso de broncoconstricción, una patología que disminuye el diámetro de los tubos bronquiales y que puede ser causada por el asma. Los atletas tienen los pulmones generalmente más parecidos al pulmón óptimo y, por tanto, son más vulnerables.
El intestino delgado. La superficie exterior del intestino delgado tiene un área aproximada de
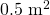 , mientras que la interior tiene es de aproximadamente
, mientras que la interior tiene es de aproximadamente 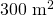 . Hemos visto en el ejemplo del copo de nieve de von Koch que una curva fractal puede tener longitud infinita, incluso aunque se en inserte una superficie finita. De manera análoga, podemos imaginar fácilmente que una superficie fractal que se inserte en un volumen finito puede tener área infinita. Este es un truco usado frecuentemente por la naturaleza: el área de la superficie interna del intestino delgado tiene que ser muy grande para poder maximizar la absorción intestinal y la naturaleza fractal de esta superficie lo permite. De la misma manera, la superficie de los alveolos al final de los braquiolos en los pulmones. COmo el árbol bronquial tiene estructura fractal, la superficie de los alveolos es extremandamente grande, maximizando el intercambio de gas.
. Hemos visto en el ejemplo del copo de nieve de von Koch que una curva fractal puede tener longitud infinita, incluso aunque se en inserte una superficie finita. De manera análoga, podemos imaginar fácilmente que una superficie fractal que se inserte en un volumen finito puede tener área infinita. Este es un truco usado frecuentemente por la naturaleza: el área de la superficie interna del intestino delgado tiene que ser muy grande para poder maximizar la absorción intestinal y la naturaleza fractal de esta superficie lo permite. De la misma manera, la superficie de los alveolos al final de los braquiolos en los pulmones. COmo el árbol bronquial tiene estructura fractal, la superficie de los alveolos es extremandamente grande, maximizando el intercambio de gas. Bibliografía
[Ma] B. Mauroy, M. Filoche, E.R. Weibel, B. ~Sapoval, An optimal bronchial tree may be dangerous, Nature, 427 (2004), 633–636.
Autor original: Christiane Rousseau.
Este mensaje está disponible en: Inglés, Francés, Alemán, Italiano, Árabe, Khmer




 Español
Español 简体中文
简体中文  English
English  Français
Français  Deutsch
Deutsch  Italiano
Italiano  العربية
العربية  Khmer
Khmer  Português
Português