Autoren: Michèle Artigue und Ferdinando Arzarello.
Übersetzt von Eva Klein und Hans-Georg Weigand (Universität Würzburg)
Hat man ein quadratisches Gitterraster gegeben, so ist es leicht dort Quadrate einzuzeichnen, deren Ecken jeweils auf Schnittpunkten der Rasterlinien liegen. Aber ist dies auch für andere regelmäßige Polygone, z.B. ein Oktagon, möglich? Die Antwort lautet „Nein“ und kann für das Achteck wie folgt bewiesen werden (Payan, 1994):
Lassen wir das Gitterraster zunächst einmal außer Acht. Jedem regelmäßigen Achteck (also einem Achteck mit gleich langen Seiten und gleich großen Winkeln) ordnen wir wie in Abbildung 2 dargestellt ein anderes Achteck zu. Den Punkt ![]() erhält man als Bildpunkt des Punktes
erhält man als Bildpunkt des Punktes ![]() durch eine 90°- Drehung gegen den Uhrzeigersinn mit Zentrum
durch eine 90°- Drehung gegen den Uhrzeigersinn mit Zentrum ![]() ,
, ![]() als Bildpunkt von durch eine 90°- Drehung gegen den Uhrzeigersinn mit Zentrum
als Bildpunkt von durch eine 90°- Drehung gegen den Uhrzeigersinn mit Zentrum ![]() , usw. Auf diese Weise erhalten wir ein weiteres regelmäßiges Achteck, welches ähnlich zum Ausgangsachteck ist und dessen Zentrum ebenfalls
, usw. Auf diese Weise erhalten wir ein weiteres regelmäßiges Achteck, welches ähnlich zum Ausgangsachteck ist und dessen Zentrum ebenfalls ![]() ist. Seine Fläche ist jedoch echt kleiner als die des ersten Achtecks.
ist. Seine Fläche ist jedoch echt kleiner als die des ersten Achtecks.
Kommen wir nun zu den regelmäßigen Polygonen zurück, deren Eckpunkte Rasterschnittpunkte sind. Jedem solchen Polygon weisen wir die Anzahl ![]() der Schnittpunkte der Gitternetzlinien zu, die komplett innerhalb des Polygons liegen (d.h. solche, die innerhalb des Polygons liegen und nicht auf einer Seitenlinie). Ist z.B.
der Schnittpunkte der Gitternetzlinien zu, die komplett innerhalb des Polygons liegen (d.h. solche, die innerhalb des Polygons liegen und nicht auf einer Seitenlinie). Ist z.B. ![]() das Pentagon aus Abbildung 3, dann gilt
das Pentagon aus Abbildung 3, dann gilt ![]() ( Zur Erinnerung: Diese Zahl steht durch den Satz von Pick in engem Zusammenhang mit der Fläche des Pentagons).
( Zur Erinnerung: Diese Zahl steht durch den Satz von Pick in engem Zusammenhang mit der Fläche des Pentagons).
Angenommen, man könnte ein regelmäßiges Achteck konstruieren, dessen Eckpunkte Schnittpunkte von Gitternetzlinien sind. Durch den zuvor beschriebenen Prozess könnten wir aus diesem wiederum ein weiteres regelmäßiges Achteck konstruieren, dessen Eckpunkte ebenfalls Schnittpunkte der Gitterlinien sind, da diese Eigenschaft bei 90°- Drehungen erhalten bleibt, wenn das Drehzentrum ein Gitternetzpunkt ist. Außerdem wäre die natürliche Zahl ![]() stets echt kleiner als
stets echt kleiner als ![]() . Wiederholt man diesen Prozess, so endet er notwendigerweise in einem Widerspruch.
. Wiederholt man diesen Prozess, so endet er notwendigerweise in einem Widerspruch.
Wir haben also die Unmöglichkeit der Existenz eines solchen Achtecks unter Verwendung einer seit Fermats Zeitalter bekannten arithmetischen Methode bewiesen: Einen Beweis durch unendlichen Abstieg. Diese Methode beruht auf der Unmöglichkeit eine streng fallende unendliche Folge natürlicher Zahlen zu bilden und bezieht sich dabei auf eine besondere Eigenschaft der Ordnung innerhalb der Menge der natürlicher Zahlen: die Eigenschaft der Wohlordnung. Diese besagt, dass jede nichtleere Teilmenge ein kleinstes Element besitzt. Nehmen wir einmal an, man könne tatsächlich eine unendliche fallende Folge ![]() positiver natürlicher Zahlen bilden. Sei
positiver natürlicher Zahlen bilden. Sei ![]() dann die Menge aller Terme der gegebenen Folge:
dann die Menge aller Terme der gegebenen Folge: ![]() .
.
Dann hat ![]() ein kleinstes Element
ein kleinstes Element ![]() . Dies ist ein Element der Folge, also existiert ein
. Dies ist ein Element der Folge, also existiert ein ![]() , so dass
, so dass ![]() gilt. Aber dann ist
gilt. Aber dann ist ![]() und
und ![]() liegt in
liegt in ![]() , ein Widerspruch zur Definition von
, ein Widerspruch zur Definition von ![]() .
.
Mathematische Induktion und die Wohlordnung von natürlichen Zahlen
Mathematische Induktion, wie sie normalerweise in der Oberstufe eingeführt wird, ist in der Tat eine Konsequenz der Wohlordnung der natürlichen Zahlen. Sie ist das dritte von Peanos Axiomen der Arithmetik (1908) und wird wie folgt formuliert:
„Wenn ![]() eine Menge ist die
eine Menge ist die ![]() enthält und wenn für jedes Element
enthält und wenn für jedes Element ![]() in
in ![]() der Nachfolger von
der Nachfolger von ![]() ebenfalls in
ebenfalls in ![]() enthalten ist, dann enthält
enthalten ist, dann enthält ![]() jede natürliche Zahl .“
jede natürliche Zahl .“
Wir umschreiben dies normalerweise wie folgt: Wenn eine Eigenschaft ![]() von natürlichen Zahlen sowohl von
von natürlichen Zahlen sowohl von ![]() als auch jedem Nachfolger
als auch jedem Nachfolger ![]() einer jeden natürlichen Zahl angenommen wird, die diese Eigenschaft besitzt, so wird
einer jeden natürlichen Zahl angenommen wird, die diese Eigenschaft besitzt, so wird ![]() von allen natürlichen Zahlen angenommen.
von allen natürlichen Zahlen angenommen.
Nimmt man an, dass die Ordnung natürlicher Zahlen eine wohlgeordnete Relation ist, dann ist die mathematische Induktion eine direkte Konsequenz daraus. Denn angenommen, die Eigenschaft ![]() würde nicht von allen natürlichen Zahlen angenommen, und
würde nicht von allen natürlichen Zahlen angenommen, und ![]() sei die Menge der natürlichen Zahlen, die diese Eigenschaft nicht annehmen. Dann ist
sei die Menge der natürlichen Zahlen, die diese Eigenschaft nicht annehmen. Dann ist ![]() nicht leer, da sie ein kleinstes Element
nicht leer, da sie ein kleinstes Element ![]() enthält und
enthält und ![]() ist ungleich
ist ungleich ![]() , da
, da ![]() die Eigenschaft
die Eigenschaft ![]() besitzt. Damit hat
besitzt. Damit hat ![]() einen Vorgänger
einen Vorgänger ![]() , der nicht in
, der nicht in ![]() enthalten ist. Aber dann nimmt
enthalten ist. Aber dann nimmt ![]() und damit auch
und damit auch ![]()
![]() an, im Widerspruch zur Definition von
an, im Widerspruch zur Definition von ![]() .
.
Mathematische Induktion kann auch zur Definition von Funktionen genutzt werden. Man nutzt dies zum Beispiel, wenn man eine Folge durch Induktion definiert, indem man eine Relation ![]() aufstellt, wobei
aufstellt, wobei ![]() eine auf
eine auf ![]() definierte Funktion ist und als ersten Term
definierte Funktion ist und als ersten Term ![]() hat. Man nennt dies auch eine Definition durch Induktion.
hat. Man nennt dies auch eine Definition durch Induktion.
Rekursion und Induktion: Erste Verallgemeinerung
Allgemeiner gesehen kann man bei jeder wohlgeordneten Menge eine induktive Denkweise verwenden. Betrachtet man zum Beispiel die Menge ![]() mit lexikographischer Ordnung
mit lexikographischer Ordnung ![]() , falls
, falls ![]() oder
oder ![]() und
und ![]() gilt. Diese Ordnung ist eine wohlgeordnete Relation. Sei
gilt. Diese Ordnung ist eine wohlgeordnete Relation. Sei ![]() eine nichtleere Teilmenge von
eine nichtleere Teilmenge von ![]() , so erhalten wir zwei Fälle:
, so erhalten wir zwei Fälle:
- Fall 1: Alle Elemente von
 haben die Form
haben die Form 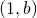 . Dann ist
. Dann ist 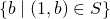 eine nichtleere Teilmenge von
eine nichtleere Teilmenge von 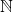 und besitzt ein kleinstes Element
und besitzt ein kleinstes Element 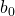 .
. 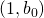 ist damit das kleinste Element von
ist damit das kleinste Element von  .
. - Fall 2: Es gibt ein Element von
 von der Form
von der Form 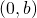 . Um zu zeigen, dass
. Um zu zeigen, dass  ein kleinstes Element besitzt, muss man beweisen dass
ein kleinstes Element besitzt, muss man beweisen dass 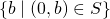 ein kleinstes Element besitzt, was jedoch offensichtlich der Fall ist.
ein kleinstes Element besitzt, was jedoch offensichtlich der Fall ist.
In ähnlicher Weise lässt sich zeigen, dass die lexikographische Ordnung von ![]() eine Wohlordnung ist. Die Anwendung des vorherigen Beweises wird in diesem Fall der Leserin oder dem Leser überlassen. Demzufolge kann es keine unendliche strengmonotonfallende Folge in diesen Mengen geben, selbst wenn für jedes Element der Form
eine Wohlordnung ist. Die Anwendung des vorherigen Beweises wird in diesem Fall der Leserin oder dem Leser überlassen. Demzufolge kann es keine unendliche strengmonotonfallende Folge in diesen Mengen geben, selbst wenn für jedes Element der Form ![]() mit
mit ![]() unendlich viele kleinere Elemente der Form
unendlich viele kleinere Elemente der Form ![]() mit
mit ![]() existieren.
existieren.
Das Prinzip des unendlichen Abstiegs aus dem ersten Beispiel kann auch in ![]() angewendet werden. Außerdem kann man in
angewendet werden. Außerdem kann man in ![]() ebenfalls Funktionen durch Induktion definieren. Dies ist zum Beispiel der Fall für die von Ackermann 1932 definierte Funktion von
ebenfalls Funktionen durch Induktion definieren. Dies ist zum Beispiel der Fall für die von Ackermann 1932 definierte Funktion von ![]() nach
nach ![]() , die später noch näher erläutert wird.
, die später noch näher erläutert wird.
Induktion und Ordinalzahlen
In der Mengentheorie drückt sich das für mathematische Beweise essentielle Konzept der Wohlordnung im Konzept der Ordinalzahlen aus und beschreibt nicht nur die bereits oben dargestellten Wohlordnungsrelationen. Ordinalzahlen, und damit auch natürliche Zahlen als endliche Ordinalzahlen, sind als wohlgeordnete Mengen durch Zugehörigkeit und Transitivität definiert (eine Menge ![]() ist transitiv, wenn alle Elemente
ist transitiv, wenn alle Elemente ![]() eines Elements
eines Elements ![]() von
von ![]() auch ein Element der Menge
auch ein Element der Menge ![]() sind). In diesem Artikel wird jedoch nur ein intuitiver Zugang zu transfiniten Ordinalzahlen betrachtet, die Ende des 19. Jahrhunderts von Cantor eingeführt wurden. Die kleinste unendliche Ordinalzahl wird als
sind). In diesem Artikel wird jedoch nur ein intuitiver Zugang zu transfiniten Ordinalzahlen betrachtet, die Ende des 19. Jahrhunderts von Cantor eingeführt wurden. Die kleinste unendliche Ordinalzahl wird als ![]() bezeichnet und ist die Vereinigung aller endlichen Ordinalzahlen. Sie repräsentiert die Ordnung auf den natürlichen Zahlen. Sie besitzt einen Nachfolger
bezeichnet und ist die Vereinigung aller endlichen Ordinalzahlen. Sie repräsentiert die Ordnung auf den natürlichen Zahlen. Sie besitzt einen Nachfolger ![]() , der wiederum einen Nachfolger
, der wiederum einen Nachfolger ![]() besitzt, usw. Die kleinste Ordinalzahl, die größer als jedes
besitzt, usw. Die kleinste Ordinalzahl, die größer als jedes ![]() ist, ist
ist, ist ![]() oder
oder ![]() . Die kleinste Ordinalzahl, die größer ist als jedes
. Die kleinste Ordinalzahl, die größer ist als jedes ![]() , ist
, ist ![]() usw.
usw.
![]()
Es gibt in der Tat zwei verschiedene Arten von Ordinalzahlen: Diejenigen, die Nachfolger einer gegebenen Ordinalzahl sind, wie z.B. ![]() ,
, ![]() , für
, für ![]() , und diejenigen, die keinen Vorgänger besitzen, sondern Vereinigungen aller kleineren Ordinalzahlen sind, wie z.B.
, und diejenigen, die keinen Vorgänger besitzen, sondern Vereinigungen aller kleineren Ordinalzahlen sind, wie z.B. ![]() ,
, ![]() ,
, ![]() in der vorherigen Liste. Man stellt fest, dass die lexikographische Ordnung von
in der vorherigen Liste. Man stellt fest, dass die lexikographische Ordnung von ![]() dieser Menge eine Ordnung zuweist, die der Ordnung der Ordinalzahl
dieser Menge eine Ordnung zuweist, die der Ordnung der Ordinalzahl ![]() entspricht. Die Verallgemeinerung der lexikographischen Ordnung von
entspricht. Die Verallgemeinerung der lexikographischen Ordnung von ![]() entspricht der von
entspricht der von ![]() , … Aber es gibt viele andere Ordinalzahlen außer den hier benannten, und jede davon ist abzählbar. Durch die Mengentheorie kann unter Verwendung des Auswahlaxioms bewiesen werden, dass jede Menge wohlgeordnet sein kann.
, … Aber es gibt viele andere Ordinalzahlen außer den hier benannten, und jede davon ist abzählbar. Durch die Mengentheorie kann unter Verwendung des Auswahlaxioms bewiesen werden, dass jede Menge wohlgeordnet sein kann.
Durch die Induktion nach Ordinalzahlen kann man Funktionen definieren. Um eine Funktion durch Induktion nach einer Ordinalzahl ![]() zu definieren, muss man ihren Wert an der Stelle
zu definieren, muss man ihren Wert an der Stelle ![]() angeben und weiterhin wie man den Wert von
angeben und weiterhin wie man den Wert von ![]() aus den Funktionswerten vorheriger Ordinalzahlen erhält. Man beachte, dass es hilfreich ist, zwei Fälle für die Definition von
aus den Funktionswerten vorheriger Ordinalzahlen erhält. Man beachte, dass es hilfreich ist, zwei Fälle für die Definition von ![]() zu betrachten:
zu betrachten: ![]() als Grenzwert oder als Nachfolger. Über den Ordinalzahlen kann man das Prinzip des unendlichen Abstiegs anwenden – die Goodstein Vignette liefert ein gutes Beispiel für einen solchen Beweis.
als Grenzwert oder als Nachfolger. Über den Ordinalzahlen kann man das Prinzip des unendlichen Abstiegs anwenden – die Goodstein Vignette liefert ein gutes Beispiel für einen solchen Beweis.
Über die Ackermannfunktion und das Diagonalargument
Ein Beispiel für eine Funktion, die durch Induktion definiert wird, ist die schon zuvor erwähnte Ackermannfunktion. Diese wird mit ![]() bezeichnet und ist wie folgt definiert:
bezeichnet und ist wie folgt definiert:
- Für jede positive natürliche Zahl
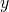 ,
, 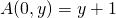
- Für jede positive natürliche Zahl
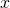 ,
, 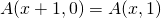
- Für jedes Paar positiver natürlicher Zahlen
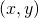 ,
, 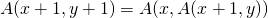 .
.
Ihr Wert an der Stelle ![]() ist dann genau gegeben, wenn
ist dann genau gegeben, wenn ![]() gleich
gleich ![]() ist. Wenn
ist. Wenn ![]() gilt, so verwendet man für die Berechnung von
gilt, so verwendet man für die Berechnung von ![]() die Werte der Funktion an gewissen Punkten
die Werte der Funktion an gewissen Punkten ![]() , sodass
, sodass ![]() für die lexikographische Ordnung gilt. Diese Berechnung benötigt eine strengmonotonfallende Folge solcher Punkte, die zwangsläufig endlich ist, da die lexikologische Ordnung eine wohlgeordnete Relation ist. Diese Folge kann jedoch sehr lang sein. Wie viele Terme sind notwendig um
für die lexikographische Ordnung gilt. Diese Berechnung benötigt eine strengmonotonfallende Folge solcher Punkte, die zwangsläufig endlich ist, da die lexikologische Ordnung eine wohlgeordnete Relation ist. Diese Folge kann jedoch sehr lang sein. Wie viele Terme sind notwendig um ![]() zu bestimmen?
zu bestimmen?
Wir beginnen mit dem einfacheren Beispiel:  A(1,0) = A(0,1) = 2
A(1,0) = A(0,1) = 2![]() A(1,1) = A(0,A(1,0)) = A(0, 2) = 3
A(1,1) = A(0,A(1,0)) = A(0, 2) = 3![]() A(1,2) = A(0,A(1,1))= A(0,3) = 4
A(1,2) = A(0,A(1,1))= A(0,3) = 4
![Rendered by QuickLaTeX.com und allgemein erhält man: <span class="ql-right-eqno"> </span><span class="ql-left-eqno"> </span><img src="https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-13c820bdd14a5098eca9ee79bd5b6595_l3.png" height="18" width="385" class="ql-img-displayed-equation " alt="\[A(1,n+1)=A(0, A(1,n))=A(0,n+1)=n+2.\]" title="Rendered by QuickLaTeX.com"/> Wir ergänzen anschließend:](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-2e80bb1c0decc234ed922abf5e695f65_l3.png)
A(2,0) = A(1,1) = 3![]() A(2,1) = A(1,A(2,0)) = A(1,3) = 5
A(2,1) = A(1,A(2,0)) = A(1,3) = 5![]() A(2,2) = A(1, A(2,1)) = A(1,5) = 7
A(2,2) = A(1, A(2,1)) = A(1,5) = 7![]() A(2,2)
A(2,2)![]() (0,6)
(0,6)![]() (1,5)
(1,5)![]() (2,2)
(2,2)![]() A(3,2)
A(3,2)![]() A(3,2)
A(3,2) A_n
A_n![]() n
n![]() A_0(y)=A(0,y)=y+1
A_0(y)=A(0,y)=y+1![]() A_0
A_0![]() A_1(y) = y + 2
A_1(y) = y + 2![]() A_2(y) = 2y+3
A_2(y) = 2y+3![]() A_3(y)=2^{y+3}-3
A_3(y)=2^{y+3}-3![]() A(x,y)
A(x,y)![]() A(5,0)=65533
A(5,0)=65533![]() A(4,2)
A(4,2)![]() g
g![]() g(x)=A(x,x)
g(x)=A(x,x)![]() \mathbb{N}^p
\mathbb{N}^p![]() \mathbb{N}
\mathbb{N}![]() N
N![]() g(x) > f(x)
g(x) > f(x)![]() x
x![]() N
N x, x+0 = x
x, x+0 = x![]() x.0=0
x.0=0![]() y, x+(y+1) = (x+y)+1
y, x+(y+1) = (x+y)+1![]() x(y+1) = xy+x
x(y+1) = xy+x![]() (x,y)
(x,y)![]() x^y
x^y k
k![]() 1
1![]() n
n \mathbb{R}
\mathbb{R}![]() \mathbb{N}
\mathbb{N}![]() X
X![]() X
X![]() X
X![]() [0,1)
[0,1)![]() [0,1)
[0,1)![]() \mathbb{N}
\mathbb{N}![]() (\alpha_n)
(\alpha_n)![]() \alpha_n
\alpha_n![]() 0
0![]() a_1^n a_2^n …
a_1^n a_2^n …![]() \alpha
\alpha![]() 0,b_1^n b_2^n …
0,b_1^n b_2^n …![]() b_k=a_k ^k -1
b_k=a_k ^k -1![]() a_k ^k \neq 0
a_k ^k \neq 0![]() b_k=a_k ^k +1
b_k=a_k ^k +1![]() a_k ^k = 0
a_k ^k = 0![]() 0,b_1 ^n b_2 ^n …
0,b_1 ^n b_2 ^n …![]() \beta
\beta![]() [0,1)
[0,1)![]() \beta
\beta![]() (a_n)
(a_n)![]() [0,1)$ nicht abzählbar und die Menge der reellen Zahlen auch nicht.
[0,1)$ nicht abzählbar und die Menge der reellen Zahlen auch nicht.
Fazit
Das Prinzip der mathematischen Induktion ist nun schon seit dem Altertum in Gebrauch. Beispielsweise wird es in Euklids Elementen verwendet, um zu zeigen, dass es unendlich viele Primzahlen gibt. Auch das Prinzip des unendlichen Abstiegs wird seit Hunderten von Jahren genutzt und wird oft mit Fermat in Verbindung gebracht, der es wiederholt in seinem Werk zur Zahlentheorie verwendete. Auf die Äquivalenz dieser beiden Prinzipien wird jedoch erst seit Kurzem hingewiesen, eine Tatsache, die auf der Entwicklung der mathematischen Logik beruht. Das Hauptwerkzeug hierfür ist das Konzept der Wohlordnung, in welchem Georg Cantor ein fundamentales „Werkzeug des Denkens“ sah. Es erlaubt uns die Äquivalenz zwischen mathematischer Induktion und unendlichem Abstieg zu erkennen, aber auch mit anderen Mengen außer den natürliche Zahlen zu arbeiten und insbesondere zu verstehen, wie Induktion mit mehr als einer Induktionsvariable funktioniert (wie Z.B. in der Ackermannfunktion).
Das Beispiel vom Beginn dieses „Klein-Artikels“ zeigt, dass mathematische Induktion ein allgemeines Werkzeug der Mathematik ist und kein alleiniges Werkzeug der Zahlentheorie. Besonders in der diskreten Mathematik spielt sie eine große Rolle.
Dieser „Klein-Artikel“ bot außerdem Anlass, viele wichtige Fragen zusätzlich zu – aber nicht unabhängig von – der Induktion zu nennen, wie z.B. die der Berechenbarkeit. Die Mathematisierung des intuitiven Konzepts der Berechenbarkeit, welche die Encodierung von verschiedenen Typen von diskreten Objekten und die Verwendung von Diagonalargumenten erfordert, hat dabei geholfen, viele wichtige Resultate in verschiedensten Feldern zu erzielen. Sie ist außerdem entscheidend für Verbindungen zwischen Mathematik und Informatik.



