Übersetzt aus dem Englischen von Eva Klein (Universität Würzburg)
Wie misst man die Größe eines geometrischen Objekts? Für Teilmengen einer Ebene verwenden wir dazu oft Umfang, Länge, Flächeninhalt, Durchmesser, etc. Diese Maßbegriffe reichen jedoch nicht aus, um Fraktale zu beschreiben. Fraktale Objekte sind sehr komplexe geometrische Objekte, für deren Komplexität wir eine Quantifizierungsmöglichkeit suchen müssen. Zu diesem Zweck bietet sich der Begriff der Dimension an. Dimension liefert uns ein Maß für die Komplexität eines Fraktals. Der Dimensionsbegriff selbst geht dabei durch Generalisierung und Formalisierung aus unserem intuitiven Dimensionsbegriff hervor, den wir verwenden, wenn wir von 1D, 2D oder 3D sprechen. Im Folgenden werden wir einige Möglichkeiten für die Beschreibung fraktaler Objekte anhand zweier Beispiele betrachten, dem Sierpinski-Teppich und der Kochschen Kurve (siehe Abbildungen oben links).
Wie groß ist der Flächeninhalt eines Sierpinski-Teppichs?
Zunächst ist es nötig, die Konstruktion des Sierpinski-Teppichs nachzuvollziehen (siehe Abbildung 2). Er entsteht durch einen Iterationsprozess: Man beginnt mit einem Dreieck und entfernt bei jedem Schritt ein Dreieck aus der Mitte. Man hat nun drei Dreiecke. In jedem dieser Dreiecke entfernt man nun das mittlere Dreieck, usw.
Jetzt haben wir alles, was zur Berechnung des Flächeninhalts des Sierpinski-Teppichs benötigt wird. Sei nun ![]() der Flächeninhalt des Anfangsdreiecks (siehe Abbildung 2(a)).
der Flächeninhalt des Anfangsdreiecks (siehe Abbildung 2(a)).
- Beim ersten Iterationsschritt entfernt man einen Flächeninhalt von
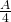 und erhält so eine Restfläche vom Inhalt
und erhält so eine Restfläche vom Inhalt 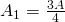 .
. - Beim zweiten Iterationsschritt entfernt man ein Viertel des Flächeninhalts der drei verbleibenden Dreiecke, also ein Viertel von
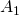 . Somit beträgt der Inhalt der restlichen Fläche
. Somit beträgt der Inhalt der restlichen Fläche 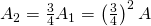 .
. - Beim dritten Iterationsschritt entfernt man ein Viertel der Fläche der neun verbleibenden Dreiecke, also ein Viertel von
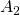 . Damit ist der verbleibende Flächeninhalt
. Damit ist der verbleibende Flächeninhalt 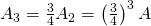 .
. - …
- Beim
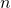 -ten Iterationsschritt entfernt man ein Viertel des Flächeninhalts der
-ten Iterationsschritt entfernt man ein Viertel des Flächeninhalts der 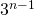 verbleibenden Dreiecke, also ein Viertel von
verbleibenden Dreiecke, also ein Viertel von 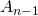 . Damit ist der Flächeninhalt der restlichen Fläche
. Damit ist der Flächeninhalt der restlichen Fläche 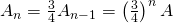 .
. - …
Wegen
![]()
sehen wir, dass der Flächeninhalt des Sierpinski-Teppichs Null ist!
Was ist die Länge der Kochschen Kurve?
Die Kochsche Kurve wird ebenfalls durch Iteration erzeugt. Bei jedem Iterationsschritt wird ein Segment durch eine Gruppe von 4 Segmenten ersetzt, wobei die Länge jedes neuen Segments einem Drittel der Länge des Ausgangssegments entspricht (siehe Abbildung 3). Sei ![]() die Länge des Ursprungsdreiecks in Abbildung 3(a). Dann ist
die Länge des Ursprungsdreiecks in Abbildung 3(a). Dann ist ![]() die Länge des Sterns in Abbildung 3(b) und
die Länge des Sterns in Abbildung 3(b) und ![]() die Länge des Objekts in Abbildung 3 (c), usw. Dies bedeutet insbesondere, dass bei jedem Iterationsschritt die Länge mit
die Länge des Objekts in Abbildung 3 (c), usw. Dies bedeutet insbesondere, dass bei jedem Iterationsschritt die Länge mit ![]() multipliziert wird. Da die Konstruktion aus unendlich vielen Schritten besteht, ist die Länge der Kochschen Kurve unendlich!
multipliziert wird. Da die Konstruktion aus unendlich vielen Schritten besteht, ist die Länge der Kochschen Kurve unendlich!
- Die Dimension eines fraktalen Objekts
Beim Sierpinski-Teppich handelt es sich um ein sehr kompliziertes Objekt. Trotzdem ist sein Flächeninhalt Null. Die Tatsache, dass die Länge der Kochschen Kurve unendlich ist, zeigt uns zwar, dass wir es mit einem komplizierten Objekt zu tun haben, doch Genaueres sagt das noch nicht aus. Um fraktale Objekte mit größerer Präzision zu beschreiben, führten Mathematiker den Dimensionsbegriff ein.
Wie definiert eine Mathematikerin oder ein Mathematiker „Dimension“?
Man beginnt mit einer intuitiven Vorstellung von Dimension. Intuitiv betrachtet haben glatte Kurven, d.h. unendlich oft stetig differenzierbare Kurven, die Dimension 1, glatte Flächen haben Dimension 2 und ausgefüllte Volumina haben Dimension 3. Daher sollten wir Dimension mathematisch so definieren, dass sie 1 für glatte Kurven, 2 für glatte Flächen und 3 für ausgefüllte Rauminhalte ergibt. Im Rahmen dieser Vignette beschränken wir uns auf Dimension 1 und 2. Wir wollen ein geometrisches Objekt in der Ebene mit kleinen Quadraten abdecken. (Für eine Definition von Dimension 3 würde man kleine Würfel verwenden, aber man hätte kleine Würfel auch für Kurven und Flächen verwenden können, ohne die Dimension zu verändern!)
Fall 1: Eine glatte Kurve. (siehe Abbildung 4)
- Verwendet man zur Abdeckung Quadrate mit einer Seitenlänge von halber Größe, so benötigt man dazu ungefähr doppelt so viele Quadrate.
- Verwendet man Quadrate mit einer Seitenlänge von einem Drittel der Ursprungsgröße, so benötigt man ungefähr dreimal so viele Quadrate, um das Objekt abzudecken.
- …
- Verwendet man Quadrate mit einer Seitenlänge, die n-mal kleiner als die Ursprungsgröße ist, so benötigt man ungefähr n-mal so viele Quadrate, um das Objekt abzudecken.
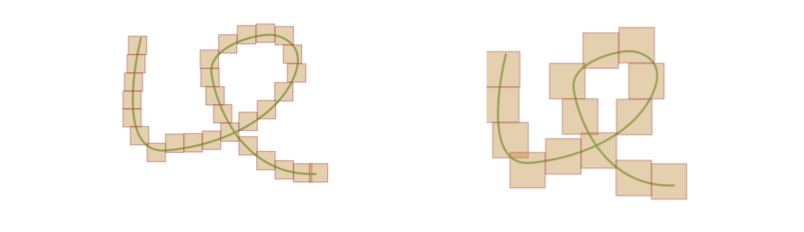
Abbildung 4: Die Berechnung der Dimension einer Kurve mit Hilfe von Quadraten unterschiedlicher Größe.
Fall 2: Eine Fläche. (siehe Abbildung 5)
- Halbiert man die Seitenlänge der verwendeten Quadrate, so benötigt man ungefähr die vierfache Anzahl an Quadraten, um das Objekt abzudecken.
- Drittelt man die Seitenlänge der verwendeten Quadrate, so benötigt man ungefähr die neunfache Anzahl an Quadraten, um das Objekt abzudecken.
- …
- Verwendet man Quadrate mit n-mal kleinerer Seitenlänge, so benötigt man ungefähr die n2-fache Anzahl an Quadraten, um das Objekt abzudecken.
Abbildung 5: Die Berechnung der Dimension einer Fläche mit Hilfe von Quadraten unterschiedlicher Größe.
Nun kann man Dimension wie folgt (intuitiv) definieren:
Definition: Ein Objekt in der Ebene hat Dimension d, wenn man, ausgehend von Quadraten mit n-fach kleinerer Seitenlänge, ungefähr die nd-fache Anzahl an Quadraten benötigt, um es vollständig abzudecken.
Einige Bemerkungen zu unserer Definition:
- Natürlich hätten die Abdeckungsquadrate auch „schräg“ gestellt sein können. Ebenso könnten sie überlappend angeordnet sein.
- Statt Quadraten hätte man auch Rechtecke gleicher Größe verwenden können, bei denen das Verhältnis r von Länge zu Breite größer als 1 ist. Damit wäre man bezüglich Dimension 1 und 2 zu denselben Ergebnissen gekommen, und ebenso im allgemeinen Fall der Dimension 2. Zur Berechnung der Dimension der Kochschen Kurve sind Rechtecke besser geeignet als Quadrate.
Die Definition kann für geometrische Objekte verallgemeinert werden, die Teilmengen von ![]() sind, wobei das Ergebnis unabhängig vom betrachteten m ist!
sind, wobei das Ergebnis unabhängig vom betrachteten m ist!
Definition: Eine Teilmenge von ![]() hat die Dimension d, wenn man, ausgehend von m-dimensionalen Hyperwürfeln n-fach kleinerer Seitenlänge, ungefähr die nd-fache Anzahl an Hyperwürfeln benötigt, um es vollständig abzudecken.
hat die Dimension d, wenn man, ausgehend von m-dimensionalen Hyperwürfeln n-fach kleinerer Seitenlänge, ungefähr die nd-fache Anzahl an Hyperwürfeln benötigt, um es vollständig abzudecken.

Abbildung 6: Anzahl von Quadraten, die benötigt werden, um den Sierpinski-Teppich aus (a) abzudecken.
Nicht alle Objekte haben eine Dimension. Die selbstähnlichen Objekte haben jedoch eine Dimension, die in den meisten Fällen keine ganze Zahl ist. Im Folgenden wollen wir die Dimension des Sierpinski-Teppichs berechnen (siehe Abbildung 6).
- Wir gehen von einem Quadrat aus, dessen Seitenlänge der Länge der Basis entspricht. Es bedeckt den Sierpinski-Teppich aus Abbildung 6(a).
- Verwendet man nun Quadrate mit halber Seitenlänge, so benötigt man drei Quadrate, um ihn abzudecken. Man beachte, dass
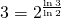 gilt (Abbildung 6(c)).
gilt (Abbildung 6(c)). - Verwendet man Quadrate mit einem Viertel der ursprünglichen Seitenlänge, so benötigt man neun Quadrate, um den Sierpinski-Teppich abzudecken. Hier gilt
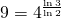 (Abbildung 6(d)).
(Abbildung 6(d)). - Verwendet man Quadrate mit einem Achtel der ursprünglichen Seitenlänge, so benötigt man 27 Quadrate, um den Sierpinski-Teppich abzudecken. Dabei ist
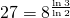 (Abbildung 6(e)).
(Abbildung 6(e)).
Dementsprechend fällt der Schluss leicht, dass die Dimension des Sierpinski-Dreiecks aus Abbildung 6(a) ![]() ist.
ist.
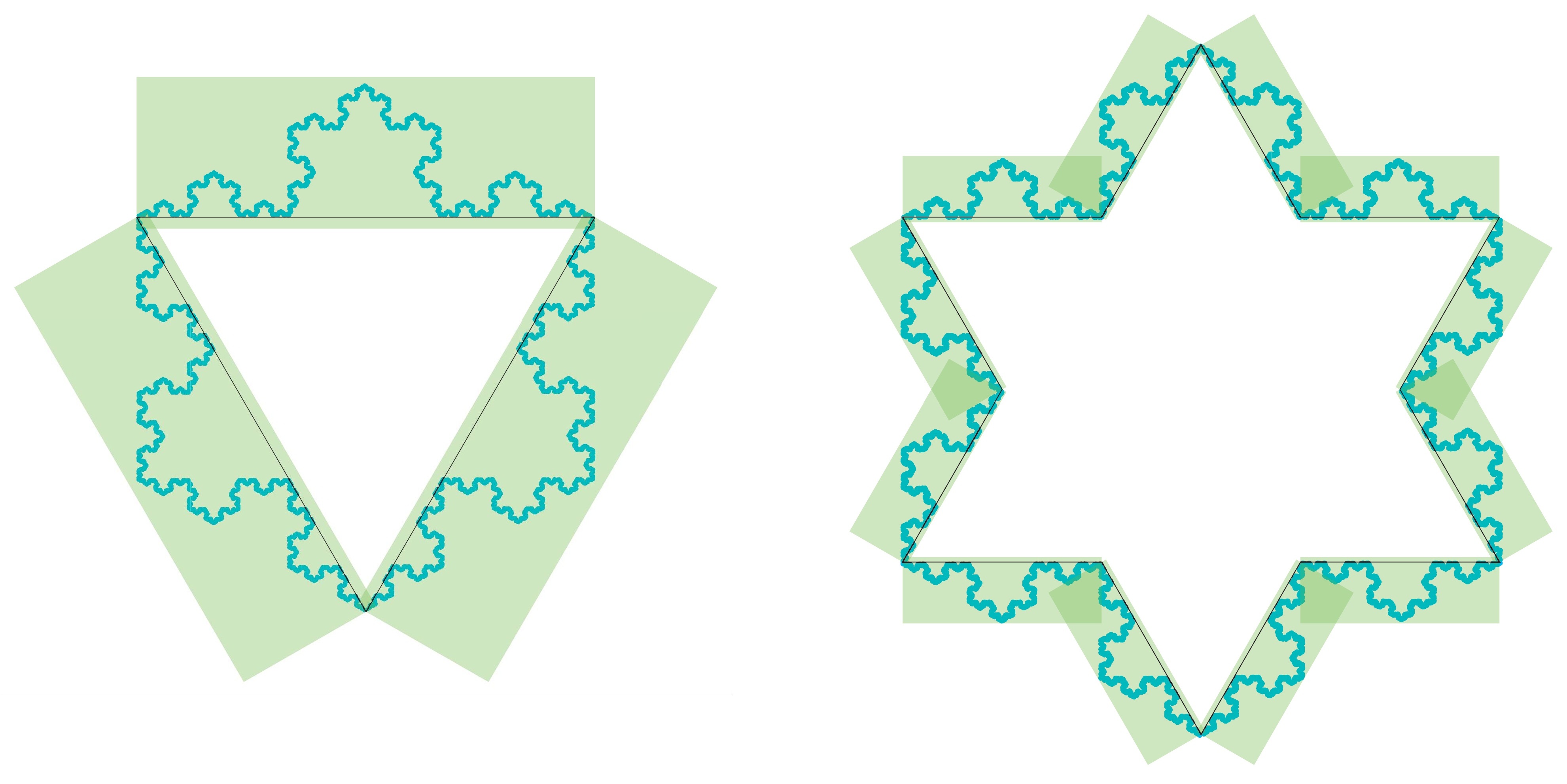
Wir stellen nun fest, dass die Kochsche Kurve aus Abbildung 1(b) die Dimension ![]() hat. Warum ist dies richtig? Versucht man, sie mit Quadraten einer Seitenlänge abzudecken, die der eines Segments aus den Iterationsschritten in Abbildung 3 entspricht, erkennt man folgende Schwierigkeit: Einige Quadrate bedecken eine Seite, andere wiederum bedecken zwei Seiten, wenn diese eine Spitze formen. Deshalb folgen wir hier dem Hinweis aus der zweiten obigen Bemerkung und verwenden Rechtecke, deren Länge das Dreifache der Breite ist.
hat. Warum ist dies richtig? Versucht man, sie mit Quadraten einer Seitenlänge abzudecken, die der eines Segments aus den Iterationsschritten in Abbildung 3 entspricht, erkennt man folgende Schwierigkeit: Einige Quadrate bedecken eine Seite, andere wiederum bedecken zwei Seiten, wenn diese eine Spitze formen. Deshalb folgen wir hier dem Hinweis aus der zweiten obigen Bemerkung und verwenden Rechtecke, deren Länge das Dreifache der Breite ist.
Wir geben hier nun die wesentlichen Schritte der Argumentation an und überlassen die Details der Leserin oder dem Leser. Bei jedem Iterationsschritt verwenden wir so viele Rechtecke wie es Seiten gibt, wobei die Länge der Rechtecke der Seitenlänge entspricht. Platziert man die Rechtecke an den Außenseiten der Kochschen Kurve, so bedecken sie die neu entstehenden Spitzen der folgenden Iterationsschritte. Man kann leicht überprüfen, dass man so viele Rechtecke wie Seiten benötigt. Im Ausgangsdreieck hatten wir drei Seiten, und da sich mit jedem Iterationsschritt die Anzahl der Seiten vervierfacht, müssen wir die Anzahl der Rechtecke entsprechend mit 4 multiplizieren. Gleichzeitig verwenden wir dann Rechtecke mit einem Drittel der vorherigen Länge. Da ![]() , erhalten wir für die Dimension der Kochschen Kurve
, erhalten wir für die Dimension der Kochschen Kurve ![]() .
.
Die Dimension liefert ein „Maß“ der Komplexität oder der Dichte eines Fraktals. Wir haben in der Tat das Gefühl, dass der Sierpinski-Teppich dichter ist als die Kochsche Kurve, die mehr einer gewöhnlichen Kurve ähnelt. Dieses Gefühl wird von der Tatsache bestätigt, dass ![]() gilt.
gilt.
Anwendungen
Das Kapillarnetz in der Nähe eines Tumors. Dieses entspricht nicht dem Kapillarnetz, das im Rest des Körpers zu finden ist. Mit dieser Tatsache beschäftigt sich die Forschung und dabei insbesondere mit der fraktalen Dimension des Kapillarnetz, mit dem Ziel, die auf medizinischer Bildgebung beruhenden Diagnosen zu verbessern.
Der Aufbau des Bronchialbaums. Professionelle Athleten haben ein höheres Asthmarisiko als der Rest der Bevölkerung. Warum ist das so? Der Artikel [Ma] befasst sich mit der „optimalen“ Lunge. 17 Abschnitte von Bronchien sind zu durchqueren bis man schließlich bei den Bronchiolen ankommt, die von den Azinuszellen, in denen der Gasaustausch stattfindet, gefolgt werden. Sind die Bronchien zu dünn, steigt der Druck wenn Luft in den nächsten Bronchialabschnitt vordringt. Sind sie zu weit, so dass das Volumen in jedem Abschnitt gleich bleibt, dann wird das Volumen am Ende zu groß (oder gar unendlich, wenn man von unendlich vielen Abschnitten ausgeht). Deshalb hätte die „optimale“ Lunge ein minimales Volumen, bei dem der Druck nicht ansteigt. In einer fast optimalen Lunge führt jedoch eine minimale Verkleinerung des Durchmessers der Bronchien schon zu einem viel höheren Druckanstieg als bei der gleichen Verkleinerung des Durchmessers in weiteren Bronchien. (Dies ist ein Resultat der speziellen nichtlinearen Form der Druck-Funktion.) Menschliche Lungen besitzen weitere Bronchien und ein größeres Volumen als die theoretisch optimale Lunge. Dieser Puffer dient als Schutz, falls es zu einer Bronchokonstriktion kommt, einer Pathologie, die den Durchmesser der Bronchien verkleinert und von Asthma verursacht werden kann. Die Lungen von Athleten sind der theoretisch optimalen Lunge generell ähnlicher und sind deshalb anfälliger.
Der Dünndarm. Die äußere Oberfläche des Dünndarms hat einen Flächeninhalt von ungefähr 0,5 m2, während der Flächeninhalt der inneren Oberfläche ungefähr 300 m2 beträgt. Anhand der Kochschen Kurve haben wir gesehen, dass eine fraktale Kurve unendliche Länge haben kann, selbst wenn sie innerhalb einer endlichen Fläche liegt. In gleicher Weise können wir uns leicht vorstellen, dass eine fraktale Fläche, die in einem endlichen Volumen liegt, einen unendlichen Flächeninhalt haben kann. Dieser Trick wird auch in der Natur angewandt: Der Flächeninhalt der inneren Oberfläche des Dünndarms muss sehr groß sein, um die intestinale Absorption zu maximieren. Die fraktale Beschaffenheit der Oberfläche führt genau zu diesem Ergebnis. Das Gleiche gilt auch für die Oberfläche der Alveolen am Ende der Bronchiolen in der Lunge. Da der Bronchialbaum ebenfalls eine fraktale Beschaffenheit hat, ist die Oberfläche der Alveolen extrem groß und maximiert so den Gasaustausch.
Bibliographie
[Ma] B. Mauroy, M. Filoche, E.R. Weibel, B. Sapoval, An optimal bronchial tree may be dangerous, Nature, 427 (2004), 633–636.
Andere Sprachen: Englisch, Französisch, Italienisch, Spanisch, Arabisch, Khmer





 Deutsch
Deutsch 简体中文
简体中文  English
English  Français
Français  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português