 Autor do original: César R. de Oliveira, Universidade Federal de São Carlos.
Autor do original: César R. de Oliveira, Universidade Federal de São Carlos.
Que trajetória seguirá uma folha flutuando em águas turbulentas? Seria mesmo possível montar um modelo matemático para prever tal movimento? Este é o mesmo tipo de problema que se enfrenta para prever o caminho dos planetas em torno do Sol? Mesmo quando conhecemos as regras que governam o movimento de um objeto, e podemos determinar as circunstâncias iniciais, verifica-se que alguns movimentos podem ser previstos e outros não. E naõ se trata apenas de uma questão de simplicidade: podemos modelar sistemas imprevisíveis com equac ̧ões muito simples. Veremos como a imprevisibilidade pode ser gerada de maneira simples. Um dos principais objetivos dos modelos téoricos é fazer (boas) previsões. Contudo, há sistemas dinâmicos determinísticos que na prática são imprevisíveis; eles são os chamados sistemas cáoticos. O objetivo deste texto é discutir como tal imprevisibilidade é gerada, e a principal ferramenta matemática aqui será a representação decimal dos números reais.
Um dos principais motivos para que modelos teóricos sejam construídos é para se fazer previsões. Contudo, existem modelos com sistemas dinâmicos determinísticos que são imprevisíveis na prática; são os chamados sistemas caóticos. O objetivo deste texto é discutir como tal imprevisibilidade pode ser gerada, e a principal ferramenta aqui será a representação decimal dos números reais.
Por sistema dinâmico determinístico deve-se entender um modelo matemático com uma lei de evolução temporal bem especificada, de forma que, se é conhecido como o sistema está disposto no presente, pode-se (teoricamente, pelo menos) saber como ele estará no futuro. Como exemplo de sistema determinístico considere um único planeta ao redor de uma estrela; tomando-se como modelo matemático a segunda lei de Newton da Mecânica Clássica, e como disposição inicial do planeta sua posição e sua velocidade em certo instante, é possível prever exatamente suas disposições futuras.
Quanto ao termo movimentos caóticos, há várias definições espalhadas pela literatura especializada. Em pelo menos um ponto há concordância: movimentos caóticos existem. No mundo dos modelos o termo caos tem sido usado como sinônimo de errático, turbulento, imprevisível, aleatório, irregular, etc., e este tem sido observado frequentemente através de simulações numéricas e em experimentos de laboratório. Tal termo em sistemas determinísticos foi cunhado por T. Li e J. A. Yorke em 1975 e “pegou”, mas seu significado neste contexto não é o apresentado num dicionário. Um exemplo cotidiano de movimento cáotico é o apresentado pelo movimento de uma pequena folha em águas turbulentas.
Destaca-se que comportamentos complicados em sistemas determinísticos não exigem equações com- plicadas! Isto possibilitou os exemplos abaixo, cujos entendimentos utilizam a representação decimal e um pouco de concentração. Passa-se então a analisar mais detalhadamente a representação decimal dos números reais e, em seguida, os exemplos. Fica aqui um convite para que os leitores peguem papel e lápis e confiram alguns dos passos apresentados abaixo.
Representação decimal
Classificam-se os números reais no intervalo ![]() em racionais e irracionais. Os racionais são aqueles que podem ser representados na forma
em racionais e irracionais. Os racionais são aqueles que podem ser representados na forma ![]() , sendo
, sendo ![]() e
e ![]() números naturais com
números naturais com ![]() e
e ![]() . Os racionais, quando representados na forma decimal, são exatamente aqueles que ou possuem apenas um número finito de dígitos não-nulos ou blocos que se repetem indefinidamente, as chamadas dízimas periódicas. Como exemplos considere
. Os racionais, quando representados na forma decimal, são exatamente aqueles que ou possuem apenas um número finito de dígitos não-nulos ou blocos que se repetem indefinidamente, as chamadas dízimas periódicas. Como exemplos considere ![]() e
e ![]() ; também podem ocorrer situações como
; também podem ocorrer situações como ![]() , que também são consideradas dízimas periódicas. Note que está sendo usado o ponto ao invés da tradicional vírgula para representar o ponto decimal.
, que também são consideradas dízimas periódicas. Note que está sendo usado o ponto ao invés da tradicional vírgula para representar o ponto decimal.
Os números irracionais são aqueles que representados na forma decimal apresentam infinitos algarismos não-nulos, mas sem que ocorram blocos que se repetem como nas dízimas periódicas; talvez o exemplo mais famoso de número irracional seja ![]() , de forma que o número
, de forma que o número ![]() também é irracional e pertence a
também é irracional e pertence a ![]() .
.
Analisando melhor os números, o que significa escrever ![]() ? O primeiro dígito
? O primeiro dígito ![]() significa, obviamente,
significa, obviamente,
que o número (ponto) considerado está entre ![]() e
e ![]() . Como a base é decimal, ou seja, são utilizados os algarismos
. Como a base é decimal, ou seja, são utilizados os algarismos ![]() para representar os números, divide-se o intervalo
para representar os números, divide-se o intervalo ![]() em dez subintervalos
em dez subintervalos
![]()
o dígito 2 em 0.25 significa que nesta primeira divisão do intervalo ![]() o número considerado está no
o número considerado está no
terceiro subintervalo. Bem, agora divide-se o terceiro subintervalo em novos dez, a saber
![]()
e o dígito 5 diz que 0.25 está, entre tais intervalos, no sexto. Como os dígitos restantes são todos nulos, tem-se que para qualquer subdivisão subsequente, tal ponto estará sempre no primeiro subintervalo que se inicia em ![]() , ficando então unicamente determinado, pois os comprimentos dos subintervalos nessa sequência tendem a zero.
, ficando então unicamente determinado, pois os comprimentos dos subintervalos nessa sequência tendem a zero.
Alguns números possuem mais de uma representação decimal. Por exemplo: ![]() é possível convencer-se disto analisando os subintervalos fechados a que
é possível convencer-se disto analisando os subintervalos fechados a que ![]() pertence (ou seja, sempre nos últimos subintervalos terminando em
pertence (ou seja, sempre nos últimos subintervalos terminando em ![]() ), ou raciocinando do seguinte modo: se
), ou raciocinando do seguinte modo: se ![]() , então
, então ![]() , logo
, logo ![]() , concluindo-se que
, concluindo-se que ![]() . Essas possíveis duplicidades de representações só ocorrem com repetições de noves a partir de certa posição (isto não é óbvio e requer uma demonstração que não será discutida aqui); no que segue, descartam-se tais representaçães particulares, garantindo unicidade da representação decimal para todos os números.
. Essas possíveis duplicidades de representações só ocorrem com repetições de noves a partir de certa posição (isto não é óbvio e requer uma demonstração que não será discutida aqui); no que segue, descartam-se tais representaçães particulares, garantindo unicidade da representação decimal para todos os números.
Usando essas ideias sobre a representação decimal, é possível, muitas vezes, construir números adequados a certos propósitos, bastando ir escolhendo subintervalos sucessivos de forma conveniente. Isto será fundamental a seguir, particularmente na descrição do sistema com propriedades caóticas.
Sistemas determinísticos e caos
Como já mencionado, num contexto dinâmico, o termo caos designa comportamentos que na prática são imprevisíveis, embora gerados por sistemas determinísticos. Mas como isso pode ocorrer? É exatamente a esta questão que se pretende apresentar uma resposta, e através da análise de um exemplo específico.
Passemos á discussão de dois sistemas dinâmicos, que numa primeira olhada podem, ingenuamente, mostrar-se assemelhados. Os dois modelos abaixo são determinísticos, o primeiro não apresenta movimento caótico e serve também para “esquentar os motores”, enquanto o segundo possui uma dinâmica bem mais rica. Muito embora esses modelos não estejam necessariamente ligados a situações físicas específicas, eles são importantes pela simplicidade de suas leis de evolução temporal, permitindo assim que as características das dinâmicas sejam mais facilmente percebidas.
Exemplo de sistema regular
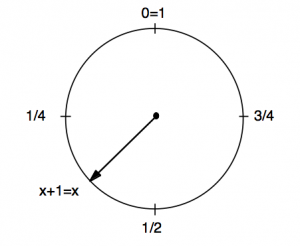
Este primeiro exemplo não apresenta caos, o que serádesignado por regular. Como disposições possíveis do sistema, considere os pontos no intervalo ![]() com uma pequena modificação: identifique seus extremos formando uma circunferência (basta imaginar um pedaço de corda com suas extremidades coladas uma á outra). A regra geral para manusear esta identificação ésimples: sempre que um número não estiver em
com uma pequena modificação: identifique seus extremos formando uma circunferência (basta imaginar um pedaço de corda com suas extremidades coladas uma á outra). A regra geral para manusear esta identificação ésimples: sempre que um número não estiver em ![]() subtrai-se sua parte inteira, o que corresponde a um número de voltas completas e, assim, retornando-se ao mesmo ponto (veja a Figura 1); como ilustração, no caso de
subtrai-se sua parte inteira, o que corresponde a um número de voltas completas e, assim, retornando-se ao mesmo ponto (veja a Figura 1); como ilustração, no caso de ![]() , a parte inteira 3 significa que três voltas completas foram dadas, não alterando a disposição do sistema, no caso
, a parte inteira 3 significa que três voltas completas foram dadas, não alterando a disposição do sistema, no caso ![]() . Vê-se também que os números 0, 1, 32 e 67 representam a mesma disposição “
. Vê-se também que os números 0, 1, 32 e 67 representam a mesma disposição “![]() “;
“; ![]() diz que partindo de zero deu-se uma volta completa e retornou-se a zero; 32 que foram dadas 32 voltas completas, e assim por diante..
diz que partindo de zero deu-se uma volta completa e retornou-se a zero; 32 que foram dadas 32 voltas completas, e assim por diante..
A evolução temporal édada por uma lei na qual só serápossível conhecer as disposições do sistema nos instantes ![]() . A lei é a seguinte: estando o sistema no instante inicial (suposto igual a zero) em
. A lei é a seguinte: estando o sistema no instante inicial (suposto igual a zero) em ![]() , então no instante um o sistema estaráem
, então no instante um o sistema estaráem ![]() , no instante dois em
, no instante dois em ![]() , e no instante genérico
, e no instante genérico ![]() em
em ![]() . Estes pontos formam a órbita de
. Estes pontos formam a órbita de ![]() e este sistema é determinístico.
e este sistema é determinístico.
É esperado que um sistema determinístico atinja algum tipo de equilíbrio para instantes muito grandes, o que em linguagem matemática significa fazer o tempo ![]() “tender ao infinito”; em símbolos:
“tender ao infinito”; em símbolos: ![]() . Neste exemplo, para
. Neste exemplo, para ![]() grande, suas disposições sucessivas se aproximam de zero, para toda condição inicial
grande, suas disposições sucessivas se aproximam de zero, para toda condição inicial ![]() ; por exemplo, se
; por exemplo, se ![]() , então
, então ![]() ,
, ![]() , etc. O equilíbrio ésempre descrito pela posição zero. É de fato um sistema regular.
, etc. O equilíbrio ésempre descrito pela posição zero. É de fato um sistema regular.
Exemplo caótico
Nesta seção seráapresentado um modelo matemático com comportamento caótico. Ele éuma simples adaptação de um sistema muito conhecido entre especialistas.
As disposições possíveis do sistema serão as mesmas ![]() do exemplo anterior, um intervalo com as extremidades identificadas. A evolução temporal édada pela seguinte lei: se a disposição inicial é
do exemplo anterior, um intervalo com as extremidades identificadas. A evolução temporal édada pela seguinte lei: se a disposição inicial é ![]() , então no instante
, então no instante ![]() o sistema estaráem
o sistema estaráem ![]() , no instante
, no instante ![]() em
em ![]() e, num instante genérico
e, num instante genérico ![]() em
em ![]() . A identificação dos pontos
. A identificação dos pontos ![]() e
e ![]() é suposta em cada instante de tempo; assim, se
é suposta em cada instante de tempo; assim, se ![]() , então
, então ![]() e
e ![]() . Aqui também tem-se um sistema determinístico.
. Aqui também tem-se um sistema determinístico.
Mas exemplifiquemos, mais uma vez, como ficam os pontos da órbita a partir da condição inicial ![]() :
: ![]() ,
, ![]() ,
, ![]() , e assim por diante.
, e assim por diante.
Seguem algumas possibilidades de equilíbrio deste sistema para ![]() :
:
Se ![]() , ou
, ou ![]() , tem-se que
, tem-se que ![]() , e o equilíbrio édescrito pela posição zero. Se
, e o equilíbrio édescrito pela posição zero. Se ![]() tem-se que
tem-se que ![]() . Ainda, se
. Ainda, se ![]() , segue que
, segue que ![]() para todo
para todo ![]() . A partir destes casos vê-se que se
. A partir destes casos vê-se que se ![]() for qualquer número racional entre zero e um, cuja representação decimal possui apenas um número finito de algarismos não-nulos, tem-se sempre como disposição de equilíbrio a posição zero.
for qualquer número racional entre zero e um, cuja representação decimal possui apenas um número finito de algarismos não-nulos, tem-se sempre como disposição de equilíbrio a posição zero.
No caso de números racionais representados por dízimas periódicas, em geral tem-se o equilíbrio dado por uma órbita periódica. O que vem a ser uma órbita periódica neste contexto pode ser compreendido
através de exemplos. No caso de ![]() tem-se
tem-se ![]() ,
, ![]() ; logo,
; logo, ![]() enquanto
enquanto ![]() , e o equilíbrio é descrito por uma órbita de período 2 dada por
, e o equilíbrio é descrito por uma órbita de período 2 dada por ![]() . Se
. Se ![]() , tem-se como equilíbrio uma órbita periódica de período
, tem-se como equilíbrio uma órbita periódica de período ![]() , ou seja,
, ou seja, ![]() , pois
, pois ![]() (e
(e ![]() se
se ![]() são distintos e pertencem a
são distintos e pertencem a ![]() . Usa-se a mesma ideia para apresentar exemplos de órbitas periódicas de qualquer período.
. Usa-se a mesma ideia para apresentar exemplos de órbitas periódicas de qualquer período.
Se a condição inicial for um número irracional, o equilíbrio pode ser mais complicado, há várias possibilidades e pode ser difícil de descrever em alguns casos; contudo, certamente nunca será uma órbita periódica (pois não se trata de uma dízima periódica) e algo relacionado serádiscutido adiante.
Uma forma prática de estimar superiormente a distância entre dois pontos em ![]() , representados na forma decimal, é contar, a partir do ponto decimal, quantos algarismos sucessivos coincidem. Por exemplo: se
, representados na forma decimal, é contar, a partir do ponto decimal, quantos algarismos sucessivos coincidem. Por exemplo: se ![]() e
e ![]() , a distância entre eles émenor ou igual a
, a distância entre eles émenor ou igual a ![]() .
.
Agora, se ![]() representa um algarismo em
representa um algarismo em ![]() e dada uma condição inicial qualquer
e dada uma condição inicial qualquer ![]() , existem condições iniciais que geram órbitas periódicas arbitrariamente próximas de
, existem condições iniciais que geram órbitas periódicas arbitrariamente próximas de ![]() (é a chamada densidade das órbitas periódicas). A nova condição inicial
(é a chamada densidade das órbitas periódicas). A nova condição inicial ![]() corresponde a uma órbita periódica de período
corresponde a uma órbita periódica de período ![]() cuja distância a
cuja distância a ![]() é menor ou igual a
é menor ou igual a ![]() (caso necessário, use blocos
(caso necessário, use blocos ![]() , com
, com ![]() ). Prosseguindo desta forma, conseguem-se órbitas periódicas de períodos altos cujas condições iniciais estão arbitrariamente próximas de
). Prosseguindo desta forma, conseguem-se órbitas periódicas de períodos altos cujas condições iniciais estão arbitrariamente próximas de ![]() . Já
. Já ![]() possui como equilíbrio o ponto zero, e sua distância a
possui como equilíbrio o ponto zero, e sua distância a ![]() émenor do que
émenor do que ![]() . A condição inicial
. A condição inicial ![]() éum número irracional cuja distância a
éum número irracional cuja distância a ![]() émenor do que
émenor do que ![]() . Como observado acima, hácondições iniciais referentes a órbitas periódicas com período arbitrariamente longo e tão perto de
. Como observado acima, hácondições iniciais referentes a órbitas periódicas com período arbitrariamente longo e tão perto de ![]() quanto se desejar.
quanto se desejar.
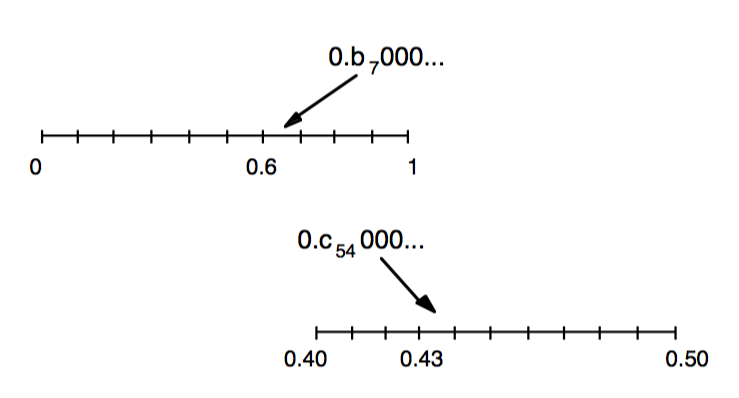
Agora considera-se um tipo de equilíbrio gerado por certos números irracionais particulares. Seja
![]()
em que ![]() são blocos constituídos por finitos algarismos entre
são blocos constituídos por finitos algarismos entre ![]() e
e ![]() , e são escolhidos como segue:
, e são escolhidos como segue:
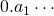 pertence a
pertence a 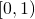 ; note que
; note que 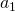 pode ser usado para localizar
pode ser usado para localizar 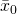 próximo de onde se desejar.
próximo de onde se desejar.- dividindo
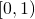 em dez subintervalos, como anteriormente,
em dez subintervalos, como anteriormente, 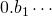 pertence ao primeiro desses subintervalos,
pertence ao primeiro desses subintervalos, 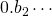 ao segundo,
ao segundo,  , e
, e 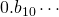 ao último. Por exemplo:
ao último. Por exemplo: 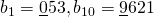 .
. - dividindo-se agora cada um dos dez subintervalos acima em dez, tem-se cem subintervalos. Escolha os
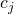 de forma que:
de forma que: 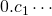 pertença ao primeiro desses subintervalos,
pertença ao primeiro desses subintervalos, 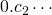 ao segundo,
ao segundo,  ,
, 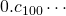 ao último. Por exemplo:
ao último. Por exemplo: 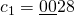 ,
, 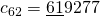 e
e 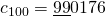 .
.
Continuando as divisões como acima, épossível conseguir condições iniciais que, pela evolução temporal, visitam “toda parte” de ![]() . Por toda parte entende-se qualquer subintervalo de
. Por toda parte entende-se qualquer subintervalo de ![]() ; o termo técnico preciso éque a órbita é densa em
; o termo técnico preciso éque a órbita é densa em ![]() . Conclui-se isto observando a órbita de
. Conclui-se isto observando a órbita de ![]() ; por exemplo, visitará
; por exemplo, visitará ![]() quanto atingir
quanto atingir ![]() , e assim por diante. Este comportamento (ou seja, visitar toda parte de
, e assim por diante. Este comportamento (ou seja, visitar toda parte de ![]() ) seria o equilíbrio dessas órbitas para
) seria o equilíbrio dessas órbitas para ![]() .
.
É interessante notar que cada um dos ![]() pode ser escolhido entre muitas possibilidades distintas, mostrando que as órbitas de infinitas condições iniciais visitam toda parte do intervalo
pode ser escolhido entre muitas possibilidades distintas, mostrando que as órbitas de infinitas condições iniciais visitam toda parte do intervalo ![]() pela evolução temporal. Háainda outras possibilidades e os leitores podem exercitar a criatividade! Pense, por exemplo, em condições iniciais cujas órbitas visitariam toda parte apenas do intervalo
pela evolução temporal. Háainda outras possibilidades e os leitores podem exercitar a criatividade! Pense, por exemplo, em condições iniciais cujas órbitas visitariam toda parte apenas do intervalo ![]() .
.
Ainda em relação à condição ![]() acima, como já indicado,
acima, como já indicado, ![]() pode ser selecionado de maneira que
pode ser selecionado de maneira que ![]() esteja arbitrariamente próximo de qualquer outro ponto de
esteja arbitrariamente próximo de qualquer outro ponto de ![]() . Assim, existem condições iniciais que pela evolução temporal se espalham por toda parte de
. Assim, existem condições iniciais que pela evolução temporal se espalham por toda parte de ![]() e que se encontram arbitrariamente próximas de qualquer órbita periódica, e também das condições iniciais cujo equilíbrio é descrito pelo zero. Tem-se, então, pelo menos três tipos de equilíbrios entrelaçados. Pode-se também considerar órbitas periódicas de diferentes períodos como tipos distintos de equilíbrio; isto é do gosto de cada autor(a) e/ou leitor(a).
e que se encontram arbitrariamente próximas de qualquer órbita periódica, e também das condições iniciais cujo equilíbrio é descrito pelo zero. Tem-se, então, pelo menos três tipos de equilíbrios entrelaçados. Pode-se também considerar órbitas periódicas de diferentes períodos como tipos distintos de equilíbrio; isto é do gosto de cada autor(a) e/ou leitor(a).
Vê-se que neste exemplo, em contraste com o anterior, para diferentes condições iniciais pode haver diferentes possibilidades de equilíbrio. O que ainda faltaria para se caracterizar o movimento caótico? É claro que esses comportamentos tão distintos entrelaçados já dão um sabor de imprevisibilidade à dinâmica, ou seja, arbitrariamente próximo a uma condição inicial existem infinitas outras que geram outros tipos de equilíbrios. Aqui entra outro ingrediente essencial: na prática as configurações iniciais de qualquer sistema são conhecidas com precisão limitada, pois sempre há um erro experimental ou de truncamento. Em sistemas físicos, aliada à precisão limitada dos dados iniciais, há também pequenas perturbações externas que podem ocorrer, como variações de temperatura e várias outras que se pode imaginar.
O quadro agora estácompleto: hácomportamentos muito distintos pela evolução temporal, cujas condições iniciais se encontram arbitrariamente próximas umas das outras e, com a precisão limitada dos dados iniciais, não se sabe qual o tipo de equilíbrio, qual comportamento para ![]() , seráseguido.
, seráseguido.
Um dos ingredientes para o comportamento caótico éa expansividade, ou seja, pontos próximos são afastados rapidamente pela evolução temporal (o que não ocorre no primeiro exemplo acima) e, neste exemplo, a cada instante de tempo a distância entre dois pontos muito próximos émultiplicada por 10; isto échamado de sensibilidade ás condições iniciais. Como ilustração, suponha que a condição inicial seja ![]() com precisão de um milionésimo, ou seja, suponha que ela possa ser qualquer ponto entre
com precisão de um milionésimo, ou seja, suponha que ela possa ser qualquer ponto entre ![]() e
e ![]() . Pela evolução temporal, no instante 1 este intervalo de precisão será multiplicado por dez e passaráa ter comprimento
. Pela evolução temporal, no instante 1 este intervalo de precisão será multiplicado por dez e passaráa ter comprimento ![]() , no instante
, no instante ![]() comprimento
comprimento ![]() , e no instante 6 comprimento 1, mas esse último é o comprimento do intervalo
, e no instante 6 comprimento 1, mas esse último é o comprimento do intervalo ![]() , ou seja, decorridos apenas 6 instantes de tempo, qualquer ponto de
, ou seja, decorridos apenas 6 instantes de tempo, qualquer ponto de ![]() pode estar descrevendo o sistema. É o caos!
pode estar descrevendo o sistema. É o caos!
Com um ferramental matemático mais sofisticado, vê-se que a evolução temporal da maioria (no sentido de exceto num conjunto de “comprimento nulo”) das condições iniciais se comporta como ![]() acima, cuja órbita édensa no intervalo
acima, cuja órbita édensa no intervalo ![]() ; assim, a condição inicial
; assim, a condição inicial ![]() ad hoc está, de fato, longe de ser uma exceção.
ad hoc está, de fato, longe de ser uma exceção.
Os exemplos acima foram definidos em termos de uma sequência de símbolos (no caso ![]() ) associados á representação decimal, dinâmicas foram postuladas e o caos dinâmico pôde se manifestar de forma clara. É interessante comentar que, muitas vezes, a partir de certos sistemas dinâmicos determinísticos mais sofisticados, alguns modelando fenômenos físicos, com ferramentas da pesquisa matemática atual pode-se visualizar (isto geralmente não é uma tarefa simples) comportamentos caóticos muito semelhantes ao descrito acima. O princípio básico éo mesmo: existência de uma região com (1) órbitas periódicas arbitrariamente próximas de qualquer condição inicial, (2) presença de órbita densa na região, e (3) sensibilidade às condições iniciais. É claro que a noção de visualização empregada acima deve ser dada de modo preciso, mas o objetivo é obter propriedades dinâmicas baseadas em símbolos como ilustrado pela representação decimal acima.
) associados á representação decimal, dinâmicas foram postuladas e o caos dinâmico pôde se manifestar de forma clara. É interessante comentar que, muitas vezes, a partir de certos sistemas dinâmicos determinísticos mais sofisticados, alguns modelando fenômenos físicos, com ferramentas da pesquisa matemática atual pode-se visualizar (isto geralmente não é uma tarefa simples) comportamentos caóticos muito semelhantes ao descrito acima. O princípio básico éo mesmo: existência de uma região com (1) órbitas periódicas arbitrariamente próximas de qualquer condição inicial, (2) presença de órbita densa na região, e (3) sensibilidade às condições iniciais. É claro que a noção de visualização empregada acima deve ser dada de modo preciso, mas o objetivo é obter propriedades dinâmicas baseadas em símbolos como ilustrado pela representação decimal acima.
Hávários aspectos do caos que não estão tratados neste texto, como suas ligações com os fractais, dimensões não-inteiras e teoria ergódica [2,6], mas o objetivo aqui não éo de uma revisão detalhada do assunto e leva, obviamente, muito do gosto do autor.
Em várias situações a presença de caos dinâmico éprejudicial: ele pode dificultar uma boa previsão meteorológica, pode ser o responsável por instabilidades planetárias, causar instabilidades aerodinâmicas, entre outros. Por outro lado, hátrabalhos apontando o caos como o mecanismo responsável pelo bom funcionamento de vários órgãos animais, como o coração e o cérebro. Assim, naturalmente pergunta-se: como características caóticas podem criar algum tipo de instabilidade responsável pelo bom funcionamento de algo? E, particularmente no caso do cérebro, como o caos é responsável por frequentemente produzir padrões originais? Certamente a situação é mais rica do que prever o comportamento de uma folha flutuante e há muitas aplicações a serem detalhadas e compreendidas.
Agradecimentos: Agradeço ao Prof. Mário J. D. Carneiro por disponibilizar seu texto sobre o assunto, bem como ao CNPq.
Referências
[1] F. L. da Silveira, Deteminismo, previsibilidade e caos, Cad. Catar. Ens. Física 10 (2) (1993), 137–147. (http://www.if.ufrgs.br/∼lang/Textos/Determinismo−previsibilidade−caos.pdf)
[2] J.-P. Eckmann, D. Ruelle, Ergodic theory of chaos and strange attractors, Rev. Modern Phys. 57 (1985), 617–656.
[3] J. Ford, How random is a coin toss?, Physics Today 36 (4) (1983), 40–47.
[4] J. Gleick, Chaos: Making a New Science, Penguin Books, Revised edition, 2008.
[5] W. M. Hirsch, S. Smale, R. Devaney, Differential Equations, Dynamical Systems, and an Introduction to Chaos, Second edition, Academic Press, New York, 2003.
[6] D. Ruelle, Chaotic Evolution and Strange Attractors, Cambridge Univ. Press, Cambridge, 1989.
[7] S. Spezamiglio, W. F. Pereira, Ordem no caos de Devaney, Matemática Universitária 35 (2003), 31–40.

 Português
Português 简体中文
简体中文  English
English  Français
Français  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer