Los autores originales son Michèle Artigue, Ferdinando Arzarello y Susanna Epp.
Los autores originales son Michèle Artigue, Ferdinando Arzarello y Susanna Epp.
El traductor del artículo al español es Pablo González Mazón (alumno de matemáticas, Universidad de Cantabria, Santander, España)
Estudiar la evolución de un fenómeno natural a menudo conduce al estudio de sucesiones numéricas, especialmente de su comportamiento para términos elevados y a decidir si, finalmente, convergen. Las sucesiones polinómicas, exponenciales y logarítmicas aparecen frecuentemente en la educación secundaria, pero otras sucesiones, con definiciones muy simples, exhiben un comportamiento mucho más complejo. Ejemplos de ello son las caóticas sucesiones que surgen en el estudio de los sistemas dinámicos (ver [1]) y la sucesión de Siracusa (o sucesión ![]() ), propuesta por Luther Collatz en 1937. La sucesión de Siracusa ha desafiado a los matemáticos durante décadas. A pesar del enorme número de valores que han sido calculados, a día de hoy se sigue sin conocer si esta sucesión es infinita o si, por el contrario, es finita y termina siempre en
), propuesta por Luther Collatz en 1937. La sucesión de Siracusa ha desafiado a los matemáticos durante décadas. A pesar del enorme número de valores que han sido calculados, a día de hoy se sigue sin conocer si esta sucesión es infinita o si, por el contrario, es finita y termina siempre en ![]() (ver [2]).
(ver [2]).
Las sucesiones consideradas en esta viñeta fueron introducidas por el lógico británico R.L. Goodstein en 1944 (ver [3]) y muestran un tipo diferente de comportamiento inusual. Sus valores iniciales aumentan tan rápidamente que es fácil creer que tienden a infinito, pero, increíblemente, siempre acaban decreciendo hasta finalmente alcanzar el cero. Demostrar este resultado requiere una generalización a los números transfinitos del principio de buena ordenación de los números naturales (ver [4]), pero la idea básica no es difícil de entender. Para explicarlo, siguiendo a Hodgson (ver [5]), primero se introduce una sucesión similar, denominada sucesión de Goodstein débil, que es más sencilla pero que está íntimamente relacionada con las sucesiones de Goodstein.
1. Sucesiones de Goodstein débiles
Siguiendo a Hodgson, se ilustra la definición de sucesión de Goodstein débil empezando por el número ![]() . Como todos los enteros positivos, este número tiene una única descomposición en suma de potencias de base
. Como todos los enteros positivos, este número tiene una única descomposición en suma de potencias de base ![]() (ver [6]):
(ver [6]): ![]() . La sucesión de Goodstein débil, de término inicial
. La sucesión de Goodstein débil, de término inicial ![]() , está definida como sigue: para obtener
, está definida como sigue: para obtener ![]() , se toma la representación de
, se toma la representación de ![]() en base
en base ![]() , y se cambia a cada una de las potencias sumadas por una potencia de base
, y se cambia a cada una de las potencias sumadas por una potencia de base ![]() con el mismo exponente; a continuación, se resta
con el mismo exponente; a continuación, se resta ![]() y se escribe el número resultante en base
y se escribe el número resultante en base ![]() . De este modo,
. De este modo, ![]() . Para determinar
. Para determinar ![]() , se empieza con la representación en base
, se empieza con la representación en base ![]() de
de ![]() , se cambia luego la base de
, se cambia luego la base de ![]() a base
a base ![]() , se resta
, se resta ![]() y se reescribe el número resultante en base
y se reescribe el número resultante en base ![]() . Así,
. Así, ![]() . Salvo en el caso de obtener cero, se continúa de esta guisa generando términos de la sucesión, reemplazando el número de la base que aparece en la expresión de un término por el siguiente número entero, restando
. Salvo en el caso de obtener cero, se continúa de esta guisa generando términos de la sucesión, reemplazando el número de la base que aparece en la expresión de un término por el siguiente número entero, restando ![]() y reescribiendo el resultado en la nueva base.
y reescribiendo el resultado en la nueva base.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Tabla 1: Términos iniciales de una sucesión de Goodstein débil.
Se observa que los términos de la sucesión toman rápidamente valores muy grandes, así que resulta fácil preguntarse si todas estas sucesiones crecen a ese ritmo. Pero no lo hacen. Por ejemplo, si el término iniciales ![]() , entonces
, entonces ![]() . Si el término inicial es
. Si el término inicial es ![]() , entonces
, entonces ![]() ,
, ![]() y
y ![]() (porque la base para
(porque la base para ![]() es
es ![]() y la base para
y la base para ![]() es
es ![]() ). No es difícil comprobar que si el término inicial es
). No es difícil comprobar que si el término inicial es ![]() , entonces los términos de la sucesión nunca toman valores mayores que
, entonces los términos de la sucesión nunca toman valores mayores que ![]() y alcanzan el
y alcanzan el ![]() en cinco pasos (ver [7]). Sin embargo, tan pronto como la descomposición para el valor inicial incluya una potencia de
en cinco pasos (ver [7]). Sin embargo, tan pronto como la descomposición para el valor inicial incluya una potencia de ![]() mayor que
mayor que ![]() , el incremento inicial de los términos es muy rápido (como se ha ilustrado para
, el incremento inicial de los términos es muy rápido (como se ha ilustrado para ![]() ), lo que parece indicar que la sucesión tiende a infinito. ¿Cómo puede el hecho de restar meramente
), lo que parece indicar que la sucesión tiende a infinito. ¿Cómo puede el hecho de restar meramente ![]() en cada paso contrarrestar al enorme incremento en los términos que se obtiene de sumar continuamente
en cada paso contrarrestar al enorme incremento en los términos que se obtiene de sumar continuamente ![]() a la base?
a la base?
Y aún más …si se observan más detenidamente las expresiones de la tabla de arriba se advertirá que, aunque los sucesivos términos de la sucesión de término inicial ![]() crecen rápidamente, los exponentes para las representaciones en las sucesivas bases tienden a disminuir. Por ejemplo, el exponente
crecen rápidamente, los exponentes para las representaciones en las sucesivas bases tienden a disminuir. Por ejemplo, el exponente ![]() en
en ![]() no vuelve a estar presente en
no vuelve a estar presente en ![]() . Paralelamente, el exponente
. Paralelamente, el exponente ![]() en
en ![]() es reemplazado por un
es reemplazado por un ![]() en
en ![]() . Y desde
. Y desde ![]() , se reduce a
, se reduce a ![]() , punto a partir del cual el coeficiente que multiplica a la base comienza a disminuir. Finalmente, el exponente
, punto a partir del cual el coeficiente que multiplica a la base comienza a disminuir. Finalmente, el exponente ![]() en
en ![]() es reducido a
es reducido a ![]() , y el
, y el ![]() sigue siendo reducido en pasos más lejanos. Esta es la característica, común a todas las sucesiones de Goodstein, que permitirá mostrar que convergen a cero. Para que pueda entenderse, es necesario recurrir, como se prometió, a los números transfinitos ordinales.
sigue siendo reducido en pasos más lejanos. Esta es la característica, común a todas las sucesiones de Goodstein, que permitirá mostrar que convergen a cero. Para que pueda entenderse, es necesario recurrir, como se prometió, a los números transfinitos ordinales.
2. Números transfinitos ordinales y la buena ordenación
Números ordinales:
En el lenguaje corriente, los números ordinales se usan para indicar la posición dentro de una lista: primero, segundo, tercero, etc. Ciertamente, los números enteros positivos pueden usarse para ordenar los elementos de cualquier conjunto finito. La idea de los números transfinitos ordinales amplía el concepto de número ordinal. Esto es debido al matemático Georg Cantor, quien los desarrolló en una serie de artículos a finales del siglo XIX. Debido a que el conjunto de los números enteros es infinito, si se imagina empezar desde el ![]() e ir contando los sucesivos enteros nunca se terminaría. Es posible, sin embargo, imaginar que hay un «número»
e ir contando los sucesivos enteros nunca se terminaría. Es posible, sin embargo, imaginar que hay un «número» ![]() , que es el primer número mayor que cualquier otro número entero. Debido a que un número infinito de números enteros son menores que él, recibe el nombre de número «transfinito». Tiene un sucesor
, que es el primer número mayor que cualquier otro número entero. Debido a que un número infinito de números enteros son menores que él, recibe el nombre de número «transfinito». Tiene un sucesor ![]() , al que sigue
, al que sigue ![]() , y de ahí en adelante. El número ordinal más pequeño mayor que todos los números ordinales de la forma
, y de ahí en adelante. El número ordinal más pequeño mayor que todos los números ordinales de la forma ![]() , se denota como
, se denota como ![]() o
o ![]() (ver [8]) y el menor número ordinal mayor que todos los números ordinales de la forma
(ver [8]) y el menor número ordinal mayor que todos los números ordinales de la forma ![]() (donde
(donde ![]() es un número ordinal menor que
es un número ordinal menor que ![]() ) se denota
) se denota ![]() . El número ordinal más pequeño mayor que todos los números ordinales de la forma
. El número ordinal más pequeño mayor que todos los números ordinales de la forma ![]() (donde ahora
(donde ahora ![]() es un número ordinal menor que
es un número ordinal menor que ![]() ) se denota por
) se denota por ![]() .
.
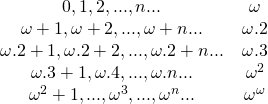
De esta manera, ![]() es seguido por
es seguido por ![]() ,
, ![]() , … ,
, … , ![]() ,
, ![]() , …,
, …, ![]() , … ,
, … , ![]() , … ,
, … , ![]() , etc., y se define
, etc., y se define ![]() como el número ordinal más pequeño mayor que todas las sumas de las potencias iteradas de
como el número ordinal más pequeño mayor que todas las sumas de las potencias iteradas de ![]() y que permite continuar el proceso indefinidamente. De hecho, todos los números ordinales considerados hasta ahora constituyen tan solo el comienzo de una cadena de números ordinales porque constituyen un conjunto numerable, esto es, que pueden ser relacionados de uno a uno con los enteros positivos.
y que permite continuar el proceso indefinidamente. De hecho, todos los números ordinales considerados hasta ahora constituyen tan solo el comienzo de una cadena de números ordinales porque constituyen un conjunto numerable, esto es, que pueden ser relacionados de uno a uno con los enteros positivos.
Números ordinales y la buena ordenación:
Una diferencia significativa entre los números transfinitos ordinales y los números enteros no negativos es que cada número entero mayor que ![]() tiene un predecesor inmediato mientras que números ordinales como
tiene un predecesor inmediato mientras que números ordinales como ![]() ,
, ![]() y
y ![]() no lo tienen. Sin embargo, como el conjunto de los números enteros, el conjunto extendido de los números ordinales está «bien ordenado» en el sentido de que todo conjunto no vacío de números ordinales tiene un mínimo. Esta propiedad es la razón por la que se puede deducir el hecho de que no puede haber una sucesión estrictamente decreciente e infinitamente larga de números ordinales. Se supone que esa sucesión infinita existe y se denotan sus términos por
no lo tienen. Sin embargo, como el conjunto de los números enteros, el conjunto extendido de los números ordinales está «bien ordenado» en el sentido de que todo conjunto no vacío de números ordinales tiene un mínimo. Esta propiedad es la razón por la que se puede deducir el hecho de que no puede haber una sucesión estrictamente decreciente e infinitamente larga de números ordinales. Se supone que esa sucesión infinita existe y se denotan sus términos por ![]() sea
sea ![]() el conjunto de todos sus términos. Dado que
el conjunto de todos sus términos. Dado que ![]() es no vacío, tiene un elemento mínimo
es no vacío, tiene un elemento mínimo ![]() , así que
, así que ![]() para algún número entero
para algún número entero ![]() . Pero como la sucesión es estrictamente decreciente,
. Pero como la sucesión es estrictamente decreciente, ![]() y
y ![]() no es el elemento mínimo de
no es el elemento mínimo de ![]() , lo que contradice la suposición.
, lo que contradice la suposición.
Se muestra ahora cómo usar los números ordinales para demostrar el resultado sobre las sucesiones de Goodstein débiles.
3. Demostración de que una sucesión de Goodstein débil converge a cero
Para cada sucesión de Goodstein débil un, se asocia una sucesión estrictamente decreciente de números ordinales αn reemplazando la base en cada término de un por ![]() . Como la base inicial de toda sucesión de Goodstein débil es
. Como la base inicial de toda sucesión de Goodstein débil es ![]() y se va incrementando en
y se va incrementando en ![]() a cada paso, la descomposición de un tiene por base de la descomposición
a cada paso, la descomposición de un tiene por base de la descomposición ![]() . De este modo, para la sucesión asociada a la sucesión de Goodstein débil de término inicial
. De este modo, para la sucesión asociada a la sucesión de Goodstein débil de término inicial ![]() , los primeros términos de
, los primeros términos de ![]() son los que se muestran en la Tabla 2:
son los que se muestran en la Tabla 2:
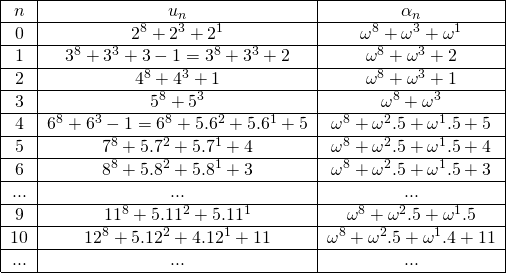
Tabla 2: Las sucesiones de números ordinales correspondientes a una sucesión de Goodstein débil (izquierda) y a su sucesión asociada (derecha).
Tal y como ha sido construida, cada término de ![]() es mayor que el correspondiente término de
es mayor que el correspondiente término de ![]() , pero mientras que
, pero mientras que ![]() está creciendo,
está creciendo, ![]() está decreciendo. La razón reside en la descomposición de un con base
está decreciendo. La razón reside en la descomposición de un con base ![]() , ya sea el término unitario de
, ya sea el término unitario de ![]() diferente de cero o no. El paso de cada término al siguiente sigue necesariamente dos posibles caminos:
diferente de cero o no. El paso de cada término al siguiente sigue necesariamente dos posibles caminos:
- Si el término de las unidades de un es distinto de cero, entonces por el hecho de que en cada paso se resta
 , el término unitario de
, el término unitario de 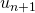 es una unidad menor que el de
es una unidad menor que el de 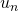 . (En la Tabla 2, esto ocurre en el paso de
. (En la Tabla 2, esto ocurre en el paso de 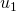 a
a 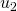 , de
, de 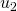 a
a 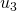 , de
, de 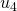 a
a 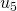 y de
y de 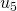 a
a 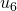 .)
.) - Si el término de las unidades de un es igual a cero, entonces cuando se reescribe la descomposición en una nueva base se tiene que reducir el término de la descomposición que tenga el menor exponente. (En la Tabla 2, esto ocurre en los pasos de
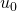 a
a 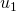 , de
, de 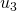 a
a 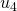 y de
y de 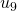 a
a 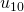 . Ver la Tabla 1 para las operaciones detalladas.) (ver [9])
. Ver la Tabla 1 para las operaciones detalladas.) (ver [9])
Se observa que en ambos casos el nuevo término de ![]() es estrictamente menor que el anterior.
es estrictamente menor que el anterior.
Ahora, debido a que los números ordinales están bien ordenados, no existe una sucesión infinita estrictamente decreciente de números ordinales, y entonces debería existir un número entero ![]() tal que
tal que ![]() . Por otra parte, como
. Por otra parte, como ![]() para todo
para todo ![]() ,
, ![]() debe igualar también a
debe igualar también a ![]() . En otras palabras, los términos de un alcanzan el
. En otras palabras, los términos de un alcanzan el ![]() en un número finito de pasos, aunque este número pueda ser extremadamente grande.
en un número finito de pasos, aunque este número pueda ser extremadamente grande.
Se invita al lector a escribir los términos de ![]() y
y ![]() empezando por
empezando por ![]() . ¿Para qué valor de
. ¿Para qué valor de ![]() se cumple que
se cumple que ![]() ¿Cuál es el valor de un entonces, y cuáles son los términos siguientes para cada una de las dos sucesiones? (ver [10]).
¿Cuál es el valor de un entonces, y cuáles son los términos siguientes para cada una de las dos sucesiones? (ver [10]).
El lector está ahora preparado para ahora abordar las sucesiones de Goodstein adecuadamente. Su definición es ligeramente diferente a la de las sucesiones de Goodstein débiles y la naturaleza de su incremento es mucho más espectacular. No obstante, sorprendentemente, la estrategia para demostrar que efectivamente disminuyen hasta cero es similar a la que se acaba de mostrar.
4. Sucesiones de Goodstein
Se considera de nuevo la representación de ![]() como suma de potencias de base
como suma de potencias de base ![]() . A continuación, se escriben los exponentes usando solo base
. A continuación, se escriben los exponentes usando solo base ![]() :
: ![]() y
y ![]() . Como resultado, la expresión completa de
. Como resultado, la expresión completa de ![]() puede realizarse sin emplear ningún número mayor que
puede realizarse sin emplear ningún número mayor que ![]() . Sea
. Sea ![]() la sucesión de Goodstein que empieza con
la sucesión de Goodstein que empieza con ![]() . Para obtener
. Para obtener ![]() , se reemplazan todos los
, se reemplazan todos los ![]() presentes en la descomposición por
presentes en la descomposición por ![]() , se resta
, se resta ![]() , y se reescribe el resultado sin utilizar un número mayor que
, y se reescribe el resultado sin utilizar un número mayor que ![]() . Se continúa repitiendo el proceso iterativamente para construir los sucesivos términos de
. Se continúa repitiendo el proceso iterativamente para construir los sucesivos términos de ![]() , como se muestra en la Tabla 3 (ver [11]).
, como se muestra en la Tabla 3 (ver [11]).
![]()
![]()
![]()
![]()
![]()
![]()
Tabla 3.
Se observa que el crecimiento en el tamaño de los términos es espectacular, y aun así, como todas las sucesiones de Goodstein, la sucesión termina por decrecer hasta finalmente converger a ![]() . La demostración es muy similar a la de la convergencia a cero de una sucesión de Goodstein débil. Como en el caso anterior, se considera una sucesión
. La demostración es muy similar a la de la convergencia a cero de una sucesión de Goodstein débil. Como en el caso anterior, se considera una sucesión ![]() asociada a la sucesión
asociada a la sucesión ![]() reemplazando la base correspondiente a cada término por
reemplazando la base correspondiente a cada término por ![]() . Los primeros términos de
. Los primeros términos de ![]() son los que siguen:
son los que siguen:
![]()
![]()
![]()
![]()
![]()
![]()
La sucesión ![]() de números ordinales es estrictamente decreciente, lo que implica que tiene un elemento mínimo, y dado que los términos siguen siendo calculados mientras no sean
de números ordinales es estrictamente decreciente, lo que implica que tiene un elemento mínimo, y dado que los términos siguen siendo calculados mientras no sean ![]() , el elemento mínimo de la sucesión es el
, el elemento mínimo de la sucesión es el ![]() . Un razonamiento similar puede emplearse para cualquier sucesión de Goodstein.
. Un razonamiento similar puede emplearse para cualquier sucesión de Goodstein.
La aritmética elemental de los números enteros a menudo recibe el nombre de aritmética de Peano, porque el matemático italiano del siglo XIX Giuseppe Peano fue quien primero postuló sus axiomas. Lo más notable de la elegante prueba dada arriba es que sale fuera de la aritmética de Peano para demostrar un teorema que puede explicarse por completo con la aritmética de Peano. En otras palabras, utiliza una teoría general de conjuntos que incluye a los números ordinales transfinitos para demostrar un teorema sobre los números enteros no negativos, que es que todas las sucesiones de Goodstein convergen a 0. Resulta natural preguntarse si la convergencia de las sucesiones de Goodstein puede ser demostrada sin utilizar los ordinales transfinitos. ¡La respuesta es que no! Esto fue demostrado en 1982, aproximadamente 40 años después de que las sucesiones fueran presentadas, por Laurie Kirby y Jeff Paris (ver [12]). Ellos mostraron que si la convergencia puede ser probada usando solamente el principio de buen orden de los números enteros (i.e., dentro de la aritmética de Peano), entonces el teorema sobre las sucesiones de Goodstein podría reducirse al teorema de Gentzen (1936), de donde la consistencia de la aritmética de Peano podría ser deducida. Pero se sabe del teorema de incompletitud de Gödel (1931) que la consistencia de la aritmética de Peano no puede ser probada usando solamente la aritmética de Peano. ¡Es por ello inútil para los matemáticos gastar sus energías en encontrar tal prueba!
Por otra parte, parece sorprendente que la convergencia a cero de una sucesión de Goodstein débil sí pueda ser demostrada dentro de la aritmética de Peano. La razón es esencialmente que los términos de la sucesión asociada de números ordinales son menores que ![]() . Una demostración fue dada por E. A. Cichon, quien introdujo las sucesionesde Goodstein débiles en 1983 (ver [13]). Para cada término de
. Una demostración fue dada por E. A. Cichon, quien introdujo las sucesionesde Goodstein débiles en 1983 (ver [13]). Para cada término de ![]() de una sucesiónde Goodstein débil, puede asociarse una
de una sucesiónde Goodstein débil, puede asociarse una ![]() -tupla de los coeficientes de la descomposición en base
-tupla de los coeficientes de la descomposición en base ![]() y mostrar que las
y mostrar que las ![]() -tuplas satisfacen un buen orden lexicográfico estrictamente decreciente.
-tuplas satisfacen un buen orden lexicográfico estrictamente decreciente.
5. Sucesionesde Goodstein y el juego de la hidra
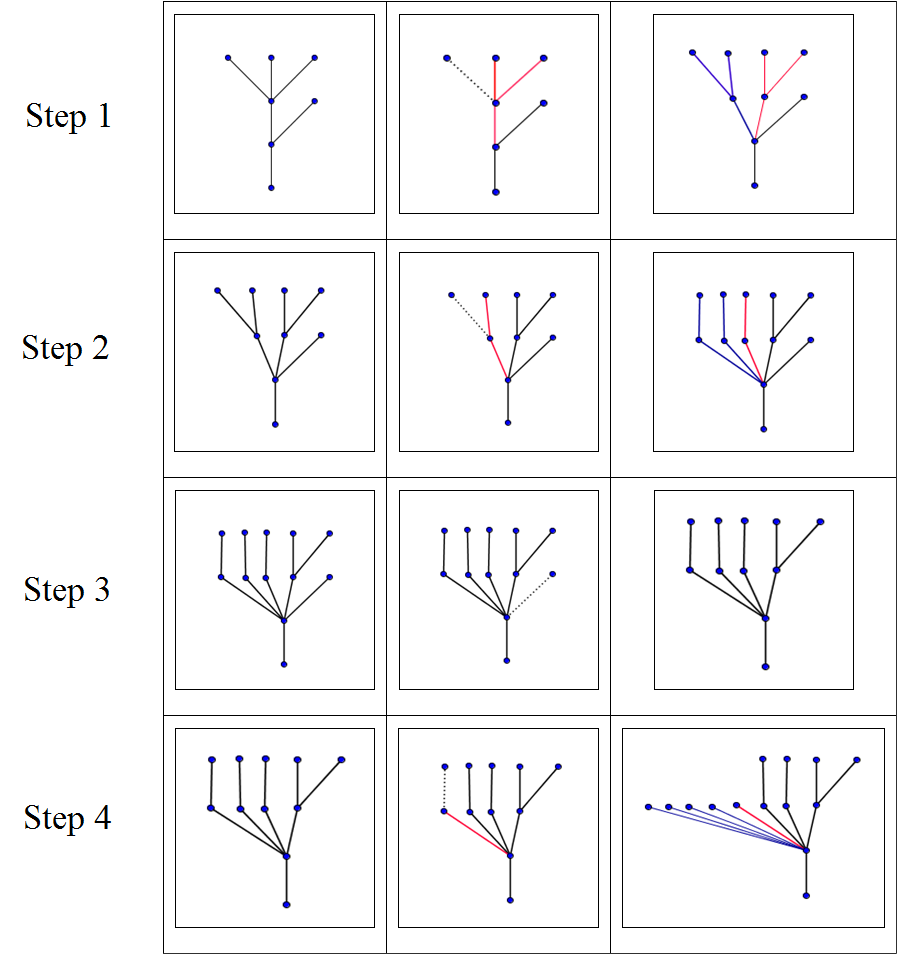
En su artículo, Kirby y Paris mencionan otro proceso, el juego de la hidra, con bastantes similitudes a las sucesiones de Goodstein. El juego (ver [14]) debe su nombre a una descripción de la mitología griega sobre el combate entre Hércules y una bestia de muchas cabezas: la hidra de Lerna. Cada vez que una de las cabezas de le hidra le era cortada, dos nuevas crecían en su lugar. En el juego, la hidra es modelizada por un árbol, y las cabezas de la hidra corresponden a los vértices finales, o las hojas del árbol. Si Hércules corta una cabeza que no está directamente conectada a la raíz del árbol, la parte por encima de la cabeza es eliminada, pero a la hidra le crecen nuevas cabezas desde el nodo de la rama localizado dos niveles por debajo de la cabeza que ha sido cortada. Esto puede llevarse a cabo de varias maneras. En el ejemplo dado por Kirby y Paris, y que Hodgson volvió a utilizar (ver [4]), si una cabeza es cortada en el paso ![]() -ésimo del juego, la hidra genera
-ésimo del juego, la hidra genera ![]() nuevas copias de la parte del árbol sobre el nodo de la rama de la que la cabeza que perdió. En el diagrama de abajo, la parte que se corta se muestra por una línea de puntos, la parte que es copiada se muestra en rojo, y la parte que es regenerada se muestra en azul.
nuevas copias de la parte del árbol sobre el nodo de la rama de la que la cabeza que perdió. En el diagrama de abajo, la parte que se corta se muestra por una línea de puntos, la parte que es copiada se muestra en rojo, y la parte que es regenerada se muestra en azul.
Es posible demostrar que sea cual sea la configuración inicial de las cabezas de la hidra, y sea cual sea la estrategia empleada por Hércules, éste siempre terminará teniendo éxito en cortar todas las cabezas, aunque podría llevarle un tiempo extraordinariamente largo hacerlo. Como para la convergencia de las sucesiones de Goodstein, la demostración está basada en la relación entre árboles sucesivos y una sucesión estrictamente decreciente de números ordinales. Es fácil intuir de los diagramas mostrados arriba que el árbol se va ensanchando a cada paso mientras que su altura va disminuyendo. Finalmente Hércules es capaz de eliminar todas las cabezas que yacen a más de un nivel sobre la raíz, y a partir de ese punto (como se ilustra en el paso 3) puede cortar las cabezas restantes de una en una sin generar ninguna nueva.
6. Lecciones de estos ejemplos
Los ejemplos en esta viñeta son interesantes por varias razones. En primer lugar, muestran que la lógica matemática es relevante para algo más que la metamatemática. Teoremas tales como el de incompletitud de Gödel u objetos como los números ordinales transfinitos son necesarios para el estudio de objetos matemáticos elementales, como las sucesiones de números enteros y los árboles matemáticos. Los ejemplos también llaman nuestra atención sobre el marco teórico y el contexto en que se producen las demostraciones, mostrando que una propiedad de los números enteros puede ser demostrada dentro de la teoría general de conjuntos pero no dentro de la aritmética de Peano. En este caso, indican que la aritmética de Peano es más débil que la teoría general de conjuntos.
Otra lección de estos ejemplos es poner en valor el enfocar un problema más difícil (la convergencia de las sucesiones de Goodstein generales) modificándolo a uno más sencillo (la convergencia de las sucesiones de Goodstein débiles). Además, muestran como un ejemplo específico – una sucesión de valor inicial ![]() – puede ilustrar todos los aspectos importantes del caso general. Los ejemplos también son interesantes porque nos hace darnos cuenta de los límites de nuestra intuición. Sucesiones que aparentemente tienden a infinito no lo hacen; en un número finito de pasos empiezan a disminuir hasta finalmente converger a
– puede ilustrar todos los aspectos importantes del caso general. Los ejemplos también son interesantes porque nos hace darnos cuenta de los límites de nuestra intuición. Sucesiones que aparentemente tienden a infinito no lo hacen; en un número finito de pasos empiezan a disminuir hasta finalmente converger a ![]() . Por último, los ejemplos nos permiten comprender tanto el poder como los límites de la aplicación de los ordenadores en matemáticas, pues si bien estos ayudan a obtener una perspectiva del aparente crecimiento rápido de los términos de la sucesión, su eficacia está limitada al enfrentarse a la explosión numérica generada por la definición de la sucesión.
. Por último, los ejemplos nos permiten comprender tanto el poder como los límites de la aplicación de los ordenadores en matemáticas, pues si bien estos ayudan a obtener una perspectiva del aparente crecimiento rápido de los términos de la sucesión, su eficacia está limitada al enfrentarse a la explosión numérica generada por la definición de la sucesión.
Referencias
[1] Elert, Glenn (1995-2007). The Chaos HypertextbookTM, Bodnar, M. & Ramsden P. Discrete Logistic Equation, Wolfram Demonstrations Project. Perrin, D. (2008). La suite logistique et le chaos.
[2] Lagarias, J. C. (2001) The Syracuse Problem. In Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer.
[3] Goodstein, R. L. (1944). On the Restricted Ordinal Theorem, Journal of Symbolic Logic, 9, 33-41.
[4] El principio de buen orden para los enteros dice que si todo elemento en un conjunto S de enteros es mayor que algún entero m, entonces S tiene elemento mínimo.
[5] Hodgson B. (2004). Herculean of Sisyphean tasks? EMS Newsletter, March 2004, pp. 11-16.
[6] Dado un entero ![]() con
con ![]() , todo entero positivo n tiene una única descomposición en base b:
, todo entero positivo n tiene una única descomposición en base b: ![]() , donde todos los di son enteros entre
, donde todos los di son enteros entre ![]() y
y ![]() y
y ![]() . Notar que
. Notar que ![]() . Esto es una generalización de la descomposición de números en base 10.
. Esto es una generalización de la descomposición de números en base 10.
[7] Si ![]() , entonces
, entonces ![]() ,
, ![]() ,
, ![]() ,
, ![]() , y
, y ![]() . Empezando por
. Empezando por ![]() , cada término sucesivo es una unidad menor que el anterior porque en cada caso la base es mayor que el término previo.
, cada término sucesivo es una unidad menor que el anterior porque en cada caso la base es mayor que el término previo.
[8] Extendemos las operaciones de suma y producto de los enteros a los ordinales transfinitos, notando, sin embargo, que la conmutatividad de la suma y multiplicación no se conserva.
[9] En general, cuando el término unitario de ![]() es cero, entonces el término más pequeño de
es cero, entonces el término más pequeño de ![]() tiene la forma
tiene la forma ![]() , donde
, donde ![]() es un entero positivo y
es un entero positivo y ![]() . Así, dado que la base es aumentada en
. Así, dado que la base es aumentada en ![]() y como se resta
y como se resta ![]() al resultado, la descomposición para
al resultado, la descomposición para ![]() termina en
termina en ![]()
De esta manera el coeficiente de la potencia menor de la base se reduce en 1 y el término unitario se convierte en uno menos que la nueva base.
[10] Las respuestas son las que siguen: ![]() cuando
cuando ![]() , y así
, y así ![]() . Para obtener
. Para obtener ![]() , reemplaza la base
, reemplaza la base ![]() por la base
por la base ![]() y resta
y resta ![]() . Por lo tanto
. Por lo tanto ![]() , entonces
, entonces ![]() . Dado que la base de
. Dado que la base de ![]() es
es ![]() y que
y que ![]() , empezando por el subíndice
, empezando por el subíndice ![]() las sucesiones
las sucesiones ![]() y
y ![]() tienen exactamente los mismos términos. Constituyen una sucesión aritmética decreciente con una diferencia constante de
tienen exactamente los mismos términos. Constituyen una sucesión aritmética decreciente con una diferencia constante de ![]() , de lo que se extrae que
, de lo que se extrae que ![]() .
.
[11] Los términos de {mn} mostrados en la Tabla 3 han sido calculados usando http://www.wolframalpha.com.
[12] Kirby, L. and Paris, J. (1982). Accessible Independence Results for Peano Arithmetic, Bulletin of the London Mathematical Society, 14, 285-293.
[13] Cichon, E. A. (1983). A Short Proof of Two Recently Discovered Independence Results Using Recursion Theoretic Methods, Proc. Amer. Math. Soc., 87, 704-706.
[14] Bauer, A. Java applet for the Hydra Game. (Si la aplicación no funciona en un programa, pruebe otro.)
https://elpais.com/elpais/2018/01/24/el_aleph/1516812203_870138.html
Miguel Angel Morales