 Vignette écrite par Christiane Rousseau.
Vignette écrite par Christiane Rousseau.
Depuis ses débuts, Google a été « le » moteur de recherche. Ceci est dû à la domination de son algorithme PageRank. En effet, avec l’énorme quantité de pages sur internet, beaucoup de recherches aboutissent à des milliers ou des millions de résultats. Si ceux-ci ne sont pas bien ordonnés, alors la recherche peut n’être d’aucune aide, puisque personne ne peut explorer des millions d’entrées.
Comment l’algorithme PageRank fonctionne-t-il?
http://www.mathunion.org/icmi/other-activities/klein-project/introduction/
plutôt que
http://www.kleinproject.org/
apparaîtra en premier dans une recherche pour Klein project.
Pour expliquer l’algorithme, on modélise le réseau internet par un graphe orienté. Les sommets sont les pages, et les arêtes orientées sont les liens entre les pages. Comme on vient de l’expliquer, chaque page correspond à une URL différente. Par conséquent, un site peut contenir de nombreuses pages. Le modèle ne fait pas de différence entre les pages individuelles d’un site et sa page d’accueil. Mais, logiquement, l’algorithme donnera un meilleur rang à la page d’accueil d’un site important.
Un exemple simple
 Regardons le réseau simple sur la gauche avec cinq pages nommées
Regardons le réseau simple sur la gauche avec cinq pages nommées ![]() ,
, ![]() ,
, ![]() ,
, ![]() , et
, et ![]() . Ce réseau a quelques liens. Si nous sommes sur la page
. Ce réseau a quelques liens. Si nous sommes sur la page ![]() , alors il n’y a qu’un lien vers la page
, alors il n’y a qu’un lien vers la page ![]() , alors que si nous sommes sur la page
, alors que si nous sommes sur la page ![]() , nous trouvons trois liens, et nous pouvons décider de nous diriger au choix vers la page
, nous trouvons trois liens, et nous pouvons décider de nous diriger au choix vers la page ![]() , ou
, ou ![]() , ou
, ou ![]() . Remarquez qu’il y a au moins un lien à partir de chaque page.
. Remarquez qu’il y a au moins un lien à partir de chaque page.
Jouons à un jeu, qui est simplement une marche aléatoire sur le graphe orienté. En partant d’une page, à chaque pas on choisit au hasard un lien partant de la page où on se trouve, et on le suit. Par exemple, dans notre graphe, si on part de la page ![]() , alors on peut aller vers
, alors on peut aller vers ![]() ou
ou ![]() avec la probabilité
avec la probabilité ![]() dans chaque cas, alors que si on part de
dans chaque cas, alors que si on part de ![]() , alors on doit nécessairement aller vers
, alors on doit nécessairement aller vers ![]() avec la probabilité
avec la probabilité ![]() . Et on répète le jeu.
. Et on répète le jeu.
![Rendered by QuickLaTeX.com \[P=\begin{matrix} \begin{matrix} A & B & C & D & E \end{matrix} & \\ \left(\ \ \begin{matrix} 0 & \frac12 & \frac13 & 1 & 0 \\ 1 & 0 & \frac13 & 0 & \frac13 \\ 0 & \frac12 & 0 & 0 & \frac13 \\ 0 & 0 & 0 & 0 & \frac13 \\ 0 & 0 & \frac13 & 0 & 0 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix} \end{matrix}\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-042ffb6838118a58c7d9602fe9856d0b_l3.png)
Remarquons que la somme des éléments de chaque colonne de ![]() est égale à
est égale à ![]() et que chaque élément de la matrice est positif ou nul. Les matrices ayant ces deux propriétés sont très spéciales: Chacune de ces matrices est la matrice d’une chaîne de Markov, aussi appelée matrice de transition de la chaîne de Markov. Elles ont toujours
et que chaque élément de la matrice est positif ou nul. Les matrices ayant ces deux propriétés sont très spéciales: Chacune de ces matrices est la matrice d’une chaîne de Markov, aussi appelée matrice de transition de la chaîne de Markov. Elles ont toujours ![]() comme valeur propre et il existe un vecteur propre de valeur propre
comme valeur propre et il existe un vecteur propre de valeur propre ![]() , dont chaque coordonnée est inférieure ou égale à
, dont chaque coordonnée est inférieure ou égale à ![]() et positive ou nulle, et tel que la somme des coordonnées est égale à
et positive ou nulle, et tel que la somme des coordonnées est égale à ![]() . Mais avant de rappeler les définitions de valeur propre et vecteur propre, explorons l’avantage de la représentation matricielle d’un graphe.
. Mais avant de rappeler les définitions de valeur propre et vecteur propre, explorons l’avantage de la représentation matricielle d’un graphe.
Considérons une variable aléatoire ![]() à valeurs dans l’ensemble des pages
à valeurs dans l’ensemble des pages ![]() contenant
contenant ![]() pages (ici
pages (ici ![]() ).
). ![]() représente la page où nous nous trouvons après
représente la page où nous nous trouvons après ![]() pas de la marche aléatoire. Par conséquent, si on appelle
pas de la marche aléatoire. Par conséquent, si on appelle ![]() l’élément de la matrice situé à l’intersection de la
l’élément de la matrice situé à l’intersection de la ![]() -ème ligne et de la
-ème ligne et de la ![]() -ème colonne, alors
-ème colonne, alors ![]() est la probabilité de se trouver sur la page
est la probabilité de se trouver sur la page ![]() à l’étape
à l’étape ![]() sachant que l’on se trouve sur la page
sachant que l’on se trouve sur la page ![]() à l’étape
à l’étape ![]() :
:
![]()
Remarquons que cette probabilité est indépendante de ![]() ! On dit qu’une chaîne de Markov n’a pas de mémoire. Il n’est pas difficile de se rendre compte que les probabilités après deux étapes sont résumées dans la matrice
! On dit qu’une chaîne de Markov n’a pas de mémoire. Il n’est pas difficile de se rendre compte que les probabilités après deux étapes sont résumées dans la matrice ![]() .
.
Prouvons-le (vous pouvez sauter la preuve si vous préférez). La formule des probabilités totales implique
![Rendered by QuickLaTeX.com \[\text{Prob}(X_{n+2}=i \mid X_n=j)=\sum_{k=1}^N\text{Prob}(X_{n+2}= i \;\text{et}\; X_{n+1}=k \mid X_n=j).\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-35a5fc26ed780ee6f5d2ae0eca982629_l3.png)
Par définition d’une probabilité conditionnelle
![Rendered by QuickLaTeX.com \[\text{Prob}(X_{n+2}=i \mid X_n=j)=\sum_{k=1}^N\frac{\text{Prob}(X_{n+2}= i \;\text{et}\; X_{n+1}=k \;\text{et}\; X_n=j)} {\text{Prob}(X_n=j)}.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-6424f56432c97ebc94e4e9c311b57b43_l3.png)
On utilise une astuce classique: On multiplie et on divise par la même quantité:
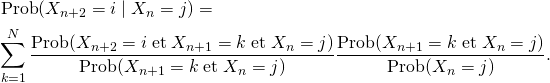
Le premier quotient est égal à
![]()
car une chaîne de Markov n’a pas de mémoire au-delà de l’étape précédente. Ainsi,
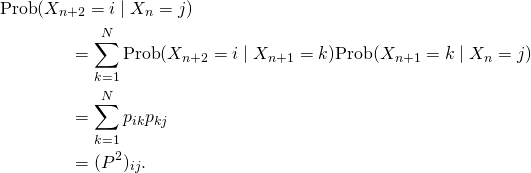
Dans notre exemple
![Rendered by QuickLaTeX.com \[P^2=\begin{matrix} \begin{matrix} A & B & C & D & E \end{matrix} & \\ \left(\ \ \begin{matrix}\frac12 & \frac16 & \frac16 & 0 & \frac{11}{18} \\ 0 & \frac23 & \frac49 & 1 & \frac19 \\ \frac12 & 0 & \frac5{18} & 0 & \frac16 \\ 0 & 0 & \frac19 & 0 & 0 \\ 0 & \frac16 & 0 & 0 & \frac19 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix} \end{matrix}\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-c815aee0d8d73d9494ae3dcdbf160507_l3.png)
Il est clair, par récurrence, que l’élément ![]() de la matrice
de la matrice ![]() est la probabilité
est la probabilité ![]() . Il se trouve que
. Il se trouve que
![Rendered by QuickLaTeX.com \[P^{32} =\begin{matrix} \begin{matrix} \:\:A \quad& \:\:B\quad & \:\:C \quad& \:\:D\quad &\:\: E \quad\end{matrix} & \\ \left(\ \ \begin{matrix} 0.293 & 0.293 & 0.293 & 0.293 & 0.293 \\ 0.390 & 0.390 & 0.390 & 0.390 & 0.390 \\ 0.220 & 0.220 & 0.220 & 0.220 & 0.220 \\ 0.024 & 0.024 & 0.024 & 0.024 & 0.024 \\ 0.073 & 0.073 & 0.073 & 0.073 & 0.073 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix}\end{matrix}\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-de62ad1480800013e6d29802e633ec19_l3.png)
Toutes les colonnes de ![]() sont identiques si on choisit d’arrondir les résultats au millème près, de même que les colonnes de
sont identiques si on choisit d’arrondir les résultats au millème près, de même que les colonnes de ![]() pour
pour ![]() . Si on choisit de garder une plus grande précision on trouvera aussi une stabilisation des résultats, mais pour
. Si on choisit de garder une plus grande précision on trouvera aussi une stabilisation des résultats, mais pour ![]() supérieur à
supérieur à ![]() . Par conséquent, après
. Par conséquent, après ![]() pas, où
pas, où ![]() est suffisamment grand, la probabilité d’être sur une page est indépendante du point de départ!
est suffisamment grand, la probabilité d’être sur une page est indépendante du point de départ!
De plus, considérons le vecteur
![]()
(![]() est un vecteur-colonne, et son transposé
est un vecteur-colonne, et son transposé ![]() est un vecteur-ligne). Il est aisé de vérifier que
est un vecteur-ligne). Il est aisé de vérifier que ![]() . Si on considère la
. Si on considère la ![]() -ème coordonnée du vecteur
-ème coordonnée du vecteur ![]() comme la probabilité d’être sur la page
comme la probabilité d’être sur la page ![]() à un moment donné
à un moment donné ![]() , et donc
, et donc ![]() comme la loi de probabilité des pages à l’instant
comme la loi de probabilité des pages à l’instant ![]() , alors il s’agit aussi de la loi de probabilité à l’instant
, alors il s’agit aussi de la loi de probabilité à l’instant ![]() . Pour cette raison, le vecteur
. Pour cette raison, le vecteur ![]() est appelé la loi stationnaire. Cette loi stationnaire permet d’ordonner les pages. Dans notre exemple, on ordonne les pages de la façon suivante:
est appelé la loi stationnaire. Cette loi stationnaire permet d’ordonner les pages. Dans notre exemple, on ordonne les pages de la façon suivante: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , et on dit que
, et on dit que ![]() est la page la plus importante.
est la page la plus importante.
Le cas général
Le cas général peut être traité exactement comme notre exemple. On représente la Toile comme un graphe orienté dans lequel les ![]() sommets représentent les
sommets représentent les ![]() pages d’internet, et les arêtes orientées représentent les liens entre les pages. On résume le graphe en une matrice
pages d’internet, et les arêtes orientées représentent les liens entre les pages. On résume le graphe en une matrice ![]() de taille
de taille ![]() , où la
, où la ![]() -ème colonne représente la
-ème colonne représente la ![]() -ème page de départ et la
-ème page de départ et la ![]() -ème ligne représente la
-ème ligne représente la ![]() -ème page d’arrivée. Dans notre exemple on a trouvé un vecteur
-ème page d’arrivée. Dans notre exemple on a trouvé un vecteur ![]() tel que
tel que ![]() . Ce vecteur est un vecteur propre de valeur propre
. Ce vecteur est un vecteur propre de valeur propre ![]() . Rappelons les définitions de valeur propre et vecteur propre.
. Rappelons les définitions de valeur propre et vecteur propre.
Définition Soit ![]() une matrice
une matrice ![]() . Un nombre
. Un nombre ![]() est une valeur propre de
est une valeur propre de ![]() s’il existe un vecteur non nul
s’il existe un vecteur non nul ![]() tel que
tel que ![]() . Un tel vecteur
. Un tel vecteur ![]() est appelé un vecteur propre de
est appelé un vecteur propre de ![]() de la valeur propre
de la valeur propre ![]() .
.
On rappelle également la méthode pour trouver les valeurs propres et vecteurs propres.
Proposition Soit ![]() une matrice
une matrice ![]() . Les valeurs propres de
. Les valeurs propres de ![]() sont les racines du polynôme caractéristique,
sont les racines du polynôme caractéristique, ![]() , où
, où ![]() la matrice identité de taille
la matrice identité de taille ![]() . Les vecteurs propres d’une valeur propre
. Les vecteurs propres d’une valeur propre ![]() sont les solutions non nulles du système linéaire homogène
sont les solutions non nulles du système linéaire homogène ![]() .
.
Le théorème suivant, dû à Perron et Frobenius, est très profond et garantit qu’une matrice associée à un graphe admet toujours une solution stationnaire.
Théorème (Théorème de Perron-Frobenius) On considère une matrice de transition d’une chaîne de Markov ![]() de taille
de taille ![]() (i.e.
(i.e. ![]() pour tout
pour tout ![]() , et la somme des éléments de chaque colonne est égale à
, et la somme des éléments de chaque colonne est égale à ![]() , c’est-à-dire
, c’est-à-dire ![]() ). Alors
). Alors
 est une valeur propre de
est une valeur propre de  .
.- Toute valeur propre
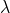 de
de 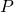 vérifie
vérifie  .
. - Il existe un vecteur propre
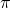 pour la valeur propre
pour la valeur propre  , dont les coordonnées sont toutes positives ou nulles. Sans perdre de généralité, on peut supposer que la somme de ses coordonnées vaut
, dont les coordonnées sont toutes positives ou nulles. Sans perdre de généralité, on peut supposer que la somme de ses coordonnées vaut  .
.
Il est maintenant temps d’admirer la puissance de ce théorème. Pour ce faire, on va supposer plus simplement que la matrice ![]() admet une base de vecteurs propres
admet une base de vecteurs propres ![]() et on va supposer que
et on va supposer que ![]() est le vecteur
est le vecteur ![]() du théorème de Perron-Frobenius. Pour chaque
du théorème de Perron-Frobenius. Pour chaque ![]() , il existe un
, il existe un ![]() tel que
tel que ![]() . Choisissons un vecteur non nul
. Choisissons un vecteur non nul ![]() tel que
tel que ![]() , où
, où ![]() et
et ![]() . On décompose
. On décompose ![]() dans la base
dans la base ![]() :
:
![Rendered by QuickLaTeX.com \[X=\sum_{i=1}^N a_iv_i.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-75c52ea84c4a0aa148f3aa2977bdb8be_l3.png)
Une preuve technique que l’on omet permet de démontrer que ![]() . Calculons maintenant
. Calculons maintenant ![]() :
:
![Rendered by QuickLaTeX.com \[PX= \sum_{i=1}^Na_i Pv_i= \sum_{i=1}^n a_i\lambda_iv_i,\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-3f5f58d838bdce8623400f20b0c3eb55_l3.png)
puisque ![]() est un vecteur propre de la valeur propre
est un vecteur propre de la valeur propre ![]() . Et si on itère ce procédé on obtient
. Et si on itère ce procédé on obtient
![Rendered by QuickLaTeX.com \[P^nX= \sum_{i=1}^n a_i\lambda_i^nv_i.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-42c385cba649519613da2a81cae3b1bb_l3.png)
Si tous les ![]() pour
pour ![]() vérifient
vérifient ![]() alors
alors
![]()
C’est exactement ce qui se passe dans notre exemple!
Remarquons cependant que le théhorème ne garantit pas qu’une matrice ![]() satisfaisant les hypothèses du théorème aura cette propriété. Décrivons les pathologies possibles et le remède.
satisfaisant les hypothèses du théorème aura cette propriété. Décrivons les pathologies possibles et le remède.
Les pathologies possibles.
- La valeur propre
 peut être une racine multiple du polynôme caractéristique
peut être une racine multiple du polynôme caractéristique  .
.
- La matrice
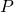 peut avoir des valeurs propres
peut avoir des valeurs propres 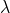 autres que
autres que  , de modules égaux à
, de modules égaux à  .
.
Que faire dans ce cas?
Une matrice de transition d’une chaîne de Markov sans pathologies est dite régulière, c’est-à-dire
Définition. Une matrice de transition d’une chaîne de Markov est régulière si
- La valeur propre
 est une racine simple du polynôme caractéristique
est une racine simple du polynôme caractéristique 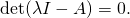
- Toute valeur propre
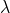 de
de 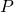 autre que
autre que  est de module strictement inférieur
est de module strictement inférieur  .
.
Remarquons que la plupart des matrices ![]() sont régulières. Si la matrice de transition d’une chaîne de Markov n’est pas régulière, la stratégie est donc de la déformer légèrement en une matrice régulière.
sont régulières. Si la matrice de transition d’une chaîne de Markov n’est pas régulière, la stratégie est donc de la déformer légèrement en une matrice régulière.
Remède. On considère la matrice ![]() de taille
de taille ![]() , avec
, avec ![]() pour tout
pour tout ![]() . On remplace la matrice
. On remplace la matrice ![]() du réseau par la matrice
du réseau par la matrice
(1) ![]()
pour un petit ![]() . (La valeur
. (La valeur ![]() a été utilisée par Google). On remarque que la matrice
a été utilisée par Google). On remarque que la matrice ![]() a encore des éléments positifs ou nuls et que la somme des éléments de chaque colonne est encore égale à
a encore des éléments positifs ou nuls et que la somme des éléments de chaque colonne est encore égale à ![]() , donc il s’agit encore d’une matrice de transition d’une chaîne de Markov. Le théorème suivant garantit qu’il existe un petit
, donc il s’agit encore d’une matrice de transition d’une chaîne de Markov. Le théorème suivant garantit qu’il existe un petit ![]() pour lequel les pathologies disparaissent.
pour lequel les pathologies disparaissent.
Théorème Étant donnée une matrice de transition d’une chaîne de Markov ![]() , il existe toujours
, il existe toujours ![]() , aussi petit que désiré, tel que la matrice
, aussi petit que désiré, tel que la matrice ![]() soit régulière. Soit
soit régulière. Soit ![]() le vecteur propre
le vecteur propre ![]() correspondant à la valeur propre
correspondant à la valeur propre ![]() , normalisé de sorte que la somme de ses coordonnées soit
, normalisé de sorte que la somme de ses coordonnées soit ![]() . Pour la matrice
. Pour la matrice ![]() , étant donné un vecteur
, étant donné un vecteur ![]() non nul quelconque, où
non nul quelconque, où ![]() avec
avec ![]() et
et ![]() , alors
, alors
(2) ![]()
Lien avec le théorème du point fixe de Banach
Une autre vignette (à venir) traite du théorème du point fixe de Banach dont le théorème ci-dessus peut être vu comme un cas particulier. Vous pouvez sauter cette partie si vous n’avez pas lu l’autre vignette. En effet,
Théorème Soit ![]() une matrice de transition d’une chaîne de Markov. On considère
une matrice de transition d’une chaîne de Markov. On considère ![]() , avec une distance
, avec une distance ![]() adéquate entre les points (cette distance dépend de
adéquate entre les points (cette distance dépend de ![]() ). On considère l’opérateur linéaire
). On considère l’opérateur linéaire ![]() défini par
défini par ![]() . L’opérateur
. L’opérateur ![]() est une contraction sur
est une contraction sur ![]() , c’est-à-dire qu’il existe
, c’est-à-dire qu’il existe ![]() tel que pour tout
tel que pour tout ![]() ,
,
![]()
Alors il existe un unique vecteur ![]() tel que
tel que ![]() .
.
De plus, étant donné ![]() quelconque, on peut définir la suite
quelconque, on peut définir la suite ![]() par récurrence, par
par récurrence, par ![]() . Alors,
. Alors, ![]() .
.
Définition de la distance ![]() . La définition de la distance
. La définition de la distance ![]() est un peu subtile et peut être sautée. On l’inclut par souci de complétude pour le lecteur désireux de connaître plus de détails. On se limite au cas où la matrice
est un peu subtile et peut être sautée. On l’inclut par souci de complétude pour le lecteur désireux de connaître plus de détails. On se limite au cas où la matrice ![]() est diagonalisable. Soit
est diagonalisable. Soit ![]() une base de vecteur propres. Les vecteurs
une base de vecteur propres. Les vecteurs ![]() peuvent être écrits dans la base
peuvent être écrits dans la base ![]() :
:
![Rendered by QuickLaTeX.com \[X=\sum_{i=1}^N a_iv_i, \quad Y=\sum_{i=1}^N b_iv_i,\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-e4878c51bc88f673f3e86656255bb8ef_l3.png)
où ![]() . On définit alors
. On définit alors
![Rendered by QuickLaTeX.com \[d(X,Y)=\sum_{i=1}^n |a_i-b_i|.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-ca97409e4ea4eb245c8b0400d97b8332_l3.png)
Muni cette distance, ![]() est un espace métrique complet, i.e. toute suite de Cauchy y est convergente.
est un espace métrique complet, i.e. toute suite de Cauchy y est convergente.
Ce théorème ne garantit pas seulement l’existence de ![]() , mais donne également une méthode pour le construire, comme limite de la suite
, mais donne également une méthode pour le construire, comme limite de la suite ![]() . Nous avons vu un exemple de cette convergence dans notre exemple. En effet, la
. Nous avons vu un exemple de cette convergence dans notre exemple. En effet, la ![]() -ème colonne de
-ème colonne de ![]() est le vecteur
est le vecteur ![]() , où
, où ![]() est le
est le ![]() -ème vecteur de la base canonique. Bien entendu, dans notre exemple nous aurions pu trouver directement le vecteur
-ème vecteur de la base canonique. Bien entendu, dans notre exemple nous aurions pu trouver directement le vecteur ![]() en résolvant le système
en résolvant le système ![]() avec la matrice
avec la matrice
![Rendered by QuickLaTeX.com \[I-P= \left(\begin{matrix} 1 &- \frac12 & -\frac13 & -1 & 0 \\ -1 & 1 & -\frac13 & 0 & -\frac13 \\ 0 & -\frac12 & 1 & 0 & -\frac13 \\ 0 & 0 & 0 & 1 & -\frac13 \\ 0 & 0 & -\frac13 & 0 & 1 \end{matrix}\right).\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-05e0ba5931bfe376391bdb5e783a74b2_l3.png)
Nous aurions découvert que toutes les solutions sont de la forme ![]() avec
avec ![]() . La solution dont la somme des coordonnées est
. La solution dont la somme des coordonnées est ![]() est donc
est donc ![]() , où
, où
![]()
Calcul pratique de la loi stationnaire
Nous avons identifié l’idée simple à la base de l’algorithme. Cependant, trouver la loi stationnaire ![]() , i.e. un vecteur propre pour la valeur propre
, i.e. un vecteur propre pour la valeur propre ![]() pour la matrice
pour la matrice ![]() dans (1) n’est pas du tout une tâche triviale lorsque la matrice a des millions de lignes et de colonnes: à la fois le temps de calcul et la capacité de mémoire nécessaires à cette réalisation sont de réels défis. La méthode classique du pivot de Gauss n’est d’aucune aide dans ce cas, à cause de la taille du calcul, et parce que la méthode nécessite des divisions par de petits coefficients. Une méthode plus efficace utilise la propriété (2) (voir [LM]). Ceci fait le lien avec la vignette à venir sur le théorème du point fixe de Banach qui montrera que la preuve du théorème fournit un algorithme pour construire le point fixe.
dans (1) n’est pas du tout une tâche triviale lorsque la matrice a des millions de lignes et de colonnes: à la fois le temps de calcul et la capacité de mémoire nécessaires à cette réalisation sont de réels défis. La méthode classique du pivot de Gauss n’est d’aucune aide dans ce cas, à cause de la taille du calcul, et parce que la méthode nécessite des divisions par de petits coefficients. Une méthode plus efficace utilise la propriété (2) (voir [LM]). Ceci fait le lien avec la vignette à venir sur le théorème du point fixe de Banach qui montrera que la preuve du théorème fournit un algorithme pour construire le point fixe.
En effet, on commence avec ![]() tel que
tel que
![]()
et on doit calculer ![]() . En général,
. En général, ![]() pour un nombre
pour un nombre ![]() entre
entre ![]() et
et ![]() donne une approximation suffisamment bonne de
donne une approximation suffisamment bonne de ![]() . Par récurrence, on calcule
. Par récurrence, on calcule ![]() . Même de tels calculs sont assez longs. En effet, de par sa construction, la matrice
. Même de tels calculs sont assez longs. En effet, de par sa construction, la matrice ![]() in (1) n’a aucun élément nul. D’un autre coté, la plupart des éléments de la matrice
in (1) n’a aucun élément nul. D’un autre coté, la plupart des éléments de la matrice ![]() sont nuls. Donc on doit décomposer le calcul pour profiter de cette propriété, c’est-à-dire
sont nuls. Donc on doit décomposer le calcul pour profiter de cette propriété, c’est-à-dire
![]()
À cause de la forme spéciale de ![]() , il est facile de vérifier que si
, il est facile de vérifier que si ![]() est un vecteur dont la somme des coordonnées vaut
est un vecteur dont la somme des coordonnées vaut ![]() , alors
, alors ![]() . Par conséquent il suffit de calculer la suite
. Par conséquent il suffit de calculer la suite
![]()
Conclusion
Nous avons présenté la partie publique de l’algorithme PageRank de Google. Vous pouvez déjà expérimenter avec des réseaux simples, et trouver les astuces permettant d’améliorer le rang de votre page personnelle en ajoutant des liens internes et externes de façon optimale. Des parties privées, et plus élaborées, continuent d’être développées. Certaines consistent à remplacer la matrice « neutre » ![]() de (1) par des matrices reflétant les goûts du promeneur sur la Toile. D’autres assurent que le classement n’est pas trop sensible aux manipulations de ceux essayant d’améliorer le classement de leurs pages.
de (1) par des matrices reflétant les goûts du promeneur sur la Toile. D’autres assurent que le classement n’est pas trop sensible aux manipulations de ceux essayant d’améliorer le classement de leurs pages.
En conclusion, qu’avons-nous observé? Une idée simple, astucieuse, a mené à une grande percée dans l’efficacité des moteurs de recherche, et à la naissance d’un empire commercial. Même si la mise en œuvre est en elle-même un exploit calculatoire, l’idée originale ne requiert que des mathématiques « élémentaires », essentiellement de l’algèbre linéaire et des probabilités. Ces outils mathématiques relativement standards, en particulier la diagonalisation de matrices, ont donné leur pleine puissance quand ils ont été utilisés en dehors de leur contexte « normal ». De plus, nous avons mis en lumière les idées unificatrices à l’intérieur de la science, avec le théorème du point fixe de Banach ayant des applications éloignées de son origine.
Bibliographie
[E] M. Eisermann, Comment Google classe les pages webb, http://images.math.cnrs.fr/Comment-Google-classe-les-pages.html, 2009.
[LM] A. N. Langville et C. D. Meyer, A Survey of Eigenvector Methods
for Web Information Retrieval, SIAM Review, Volume 47, Issue 1,
(2005), pp. 135–161.
[RS] C. Rousseau et Y. Saint-Aubin, Mathématiques et
Technologie, SUMAT Series, Springer-Verlag, 2008.

La recherche d’information sur Internet est un problème résolu par des moteurs de recherches tel que celui de Google qui se caractérise sur son choix intelligent des résultats d’une requête grâce à un algorithme, simple et efficace de «PageRank» et qui est la base de son succès !
Cette approche, faisant intervenir après une modélisation, les notions de mathématiques qui ont engendrées l’étude des chaînes de Markov, les systèmes d’équations linéaires, les vecteurs propres, les valeurs propres et même l’utilisation de quelques théorèmes d’analyse.