 Vignette écrite par Christiane Rousseau.
Vignette écrite par Christiane Rousseau.
Quel est l’empilement de sphères le plus dense? Kepler a conjecturé que c’est celui des oranges empilées que l’on peut observer sur les étales des magasins de fruits et légumes, et qui est appelé empilement cubique à faces centrées (Figure 1). Au Congrès International des Mathématiciens de 1900, David Hilbert a prononcé une conférence célèbre dans laquelle il a énoncé une liste de 23 problèmes qui marqueraient les mathématiques du 20-ième siècle. Le problème d’identifier l’empilement de sphères le plus dense, aussi appelé conjecture de Kepler, fait partie du 18-ième problème de Hilbert. La conjecture de Kepler n’a été démontrée qu’en 1998 par Thomas Hales, et les détails de la preuves ont été publiés en 2006.
1. Comment s’attaquer à de tels problèmes?
On considère différentes configurations possibles de sphères (boules pleines) de même taille, dans l’espace et, dans chaque cas, on calcule la densité de l’empilement, i.e. la proportion du volume total qui est occupé par les sphères. On appelera ![]() la densité maximale d’un empilement en dimension
la densité maximale d’un empilement en dimension ![]() . Bien sûr, cette densité dépend de la forme de la région considérée. Pour éviter cela, on considère des régions très vastes, afin que l’effet de la frontière soit négligeable. Kepler a conjecturé en 1611 que la configuration la plus dense est celle que l’on peut observer sur les étales d’oranges sur les marchés. Pourquoi a-t-il fallu tant de temps pour démontrer cette conjecture? Le problème est qu’il y a un nombre infini de configurations possibles pour les sphères. Chaque fois que l’on choisit une configuration, on peut montrer que sa densité est inférieure ou égale à celle observée sur les étales de fruits. Mais le problème est qu’on ne peut décrire qu’un nombre fini de configurations. Et même avec une unique configuration, le calcul de sa densité peut être difficile ou impossible si la configuration n’est pas périodique.
. Bien sûr, cette densité dépend de la forme de la région considérée. Pour éviter cela, on considère des régions très vastes, afin que l’effet de la frontière soit négligeable. Kepler a conjecturé en 1611 que la configuration la plus dense est celle que l’on peut observer sur les étales d’oranges sur les marchés. Pourquoi a-t-il fallu tant de temps pour démontrer cette conjecture? Le problème est qu’il y a un nombre infini de configurations possibles pour les sphères. Chaque fois que l’on choisit une configuration, on peut montrer que sa densité est inférieure ou égale à celle observée sur les étales de fruits. Mais le problème est qu’on ne peut décrire qu’un nombre fini de configurations. Et même avec une unique configuration, le calcul de sa densité peut être difficile ou impossible si la configuration n’est pas périodique.
Le problème de l’empilement de sphères le plus dense existe dans n’importe quelle dimension. Il a été résolu en 1890 pour les sphères de dimension ![]() . L’empilement de sphères dans des dimensions supérieures a des applications, par exemple pour des techniques de codes correcteurs.
. L’empilement de sphères dans des dimensions supérieures a des applications, par exemple pour des techniques de codes correcteurs.
On rencontre les mêmes difficultés dès la dimension ![]() : on ne peut pas énumérer toutes les configurations et, de plus, certaines configurations peuvent ne pas être périodiques. Nous allons montrer comment gérer ces difficultés, et montrer que l’empilement de la Figure 2(b) est la plus dense de toutes les configurations. Nous allons ensuite expliquer les difficultés de la généralisation de la peuve au cas de la dimension
: on ne peut pas énumérer toutes les configurations et, de plus, certaines configurations peuvent ne pas être périodiques. Nous allons montrer comment gérer ces difficultés, et montrer que l’empilement de la Figure 2(b) est la plus dense de toutes les configurations. Nous allons ensuite expliquer les difficultés de la généralisation de la peuve au cas de la dimension ![]() , et enfin nous discuterons brièvement des dimensions supérieures.
, et enfin nous discuterons brièvement des dimensions supérieures.
2. En dimension ![]() .
.
Considérons les deux empilements de disques de la Figure 2. Calculer la proportion de chaque carré de la figure (a) recouvert par des portions de disques, et calculer la proportion de chaque triangle de la figure (b) recouvert par des portions de disques, est un exercice facile. En faisant cela, on se rend compte que le second empilement est plus dense. En effet, l’empilement (a) a une densité de ![]() et l’empilement (b) a une densité de
et l’empilement (b) a une densité de
![]()
Chaque fois que l’on a un empilement périodique, on peut montrer qu’il a une densité inférieure à celle de l’empilement de la Figure 2 (b).
Mais comment peut-on montrer que c’est aussi le cas pour tout empilement?
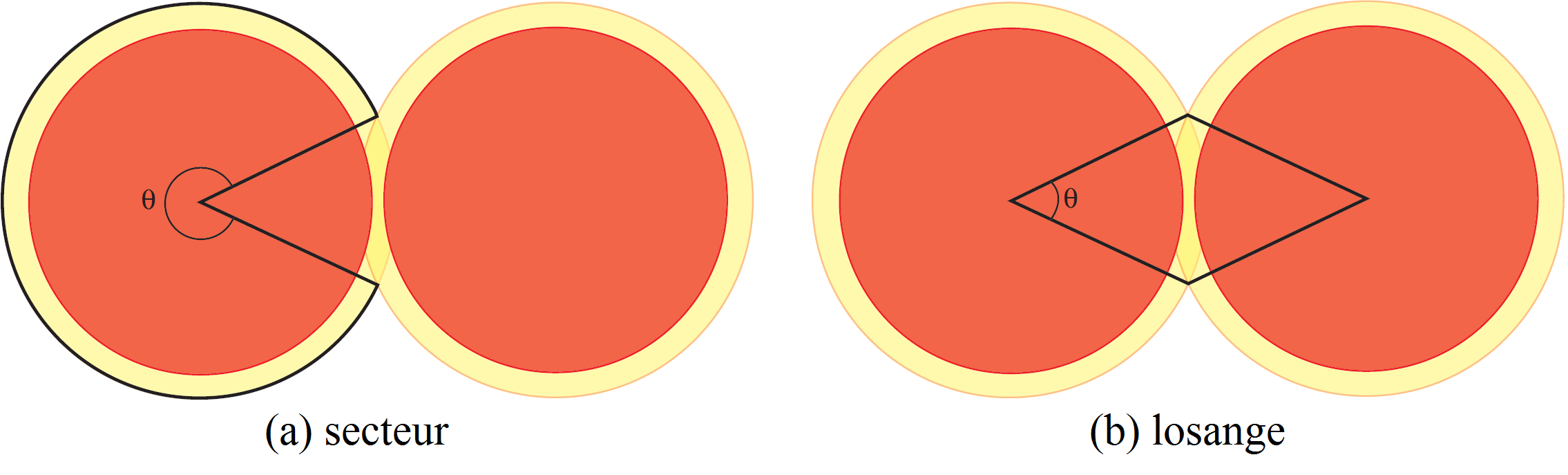
Voici une idée brillante, qui remonte au mathématicien Norvégien Axel Thue, en 1890. On découpe le plan en régions et on montre que, dans chaque région, la densité est inférieure ou égale à ![]() . Regardons la Figure 3. Nous avons là trois disques qui ne pourraient pas être plus proches les uns des autres. Regardons maintenant le triangle dont les sommets sont les centres des disques. À l’intérieur de ce triangle il y a une petite zone non recouverte par les disques. Si on agrandit les disques par un facteur
. Regardons la Figure 3. Nous avons là trois disques qui ne pourraient pas être plus proches les uns des autres. Regardons maintenant le triangle dont les sommets sont les centres des disques. À l’intérieur de ce triangle il y a une petite zone non recouverte par les disques. Si on agrandit les disques par un facteur ![]() , alors les disques agrandis remplissent totalement le triangle et ce coefficient
, alors les disques agrandis remplissent totalement le triangle et ce coefficient ![]() est le plus petit à remplir cette condition.
est le plus petit à remplir cette condition.
Nous allons utiliser cette astuce pour diviser le plan en régions adéquates. On considère un pavage du plan avec des disques de rayon ![]() . On recouvre chaque disque par un disque de même centre mais de rayon
. On recouvre chaque disque par un disque de même centre mais de rayon ![]() , que l’on appelle un grand disque. On peut maintenant définir nos trois régions. La première région est le complément de l’union des grands disques. Clairement cette région est de densité
, que l’on appelle un grand disque. On peut maintenant définir nos trois régions. La première région est le complément de l’union des grands disques. Clairement cette région est de densité ![]() . Selon la distance entre les centres des disques, les grands disques peuvent ou non se chevaucher partiellement les uns les autres. Lorsque des grands disques se chevauchent, les cercles qui les délimitent s’intersectent. On relie ces points d’intersection aux centres des disques. Ce procédé découpe les grands disques en secteurs. Il existe deux sortes de secteurs :
. Selon la distance entre les centres des disques, les grands disques peuvent ou non se chevaucher partiellement les uns les autres. Lorsque des grands disques se chevauchent, les cercles qui les délimitent s’intersectent. On relie ces points d’intersection aux centres des disques. Ce procédé découpe les grands disques en secteurs. Il existe deux sortes de secteurs :
- Les secteurs dans lesquels les grands disques ne se chevauchent pas entre eux (voir Figure 4 (a)). Dans de tels secteurs la densité est égale à
![Rendered by QuickLaTeX.com \[\frac{1}{c^2}=\frac{3}{4};\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-7a5b412bf3acabb8882fdc0cf1c6347e_l3.png)
- Les secteurs dans lesquels les grands disques se chevauchent, comme dans la Figure 4 (b). On prend ces secteurs par paires, comme sur la figure. L’union des deux secteurs est un losange et on a seulement besoin de considérer la densité à l’intérieur de ce losange. Comme la distance entre les centres des disques est d’au moins
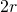 puisque les disques ne se recouvrent pas, un calcul montre que l’angle maximum pour les secteurs est
puisque les disques ne se recouvrent pas, un calcul montre que l’angle maximum pour les secteurs est 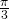 . Soit
. Soit 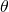 l’angle du secteur. La densité à l’intérieur du losange dépend de
l’angle du secteur. La densité à l’intérieur du losange dépend de 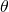 : elle est donnée par le quotient des aires des deux secteurs des disques par l’aire du losange. Chaque secteur de disque a pour aire
: elle est donnée par le quotient des aires des deux secteurs des disques par l’aire du losange. Chaque secteur de disque a pour aire 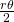 . Ainsi, l’aire du losange couverte par les disques est
. Ainsi, l’aire du losange couverte par les disques est 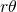 . L’aire d’un losange de coté
. L’aire d’un losange de coté 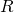 et d’angle
et d’angle 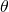 est donnée par la décomposition du losange en triangles. Elle vaut:
est donnée par la décomposition du losange en triangles. Elle vaut: 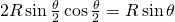 . Par conséquent la densité est
. Par conséquent la densité est
![Rendered by QuickLaTeX.com \[\mu(\theta)=\frac{r^2\theta}{R^2\sin\theta}=\frac{3\theta}{4\sin\theta}.\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-90f24f10ca630f0e9d01b943b639c102_l3.png)
Il suffit d’étudier la fonction
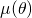 sur
sur ![Rendered by QuickLaTeX.com [0,\frac{\pi}3]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-97108dd255a2234a8ad4dd9ed1cb498f_l3.png) et de voir qu’elle atteint son maximum pour
et de voir qu’elle atteint son maximum pour 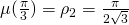 . En effet,
. En effet, 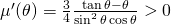 puisque
puisque 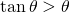 .
.
Cette preuve est extrêmement élégante. Examinons en détail certaines de ces caractéristiques. La meilleure densité est ![]() . C’est aussi la meilleure densité localement dans chaque région du plan que nous avons considéré.
. C’est aussi la meilleure densité localement dans chaque région du plan que nous avons considéré.
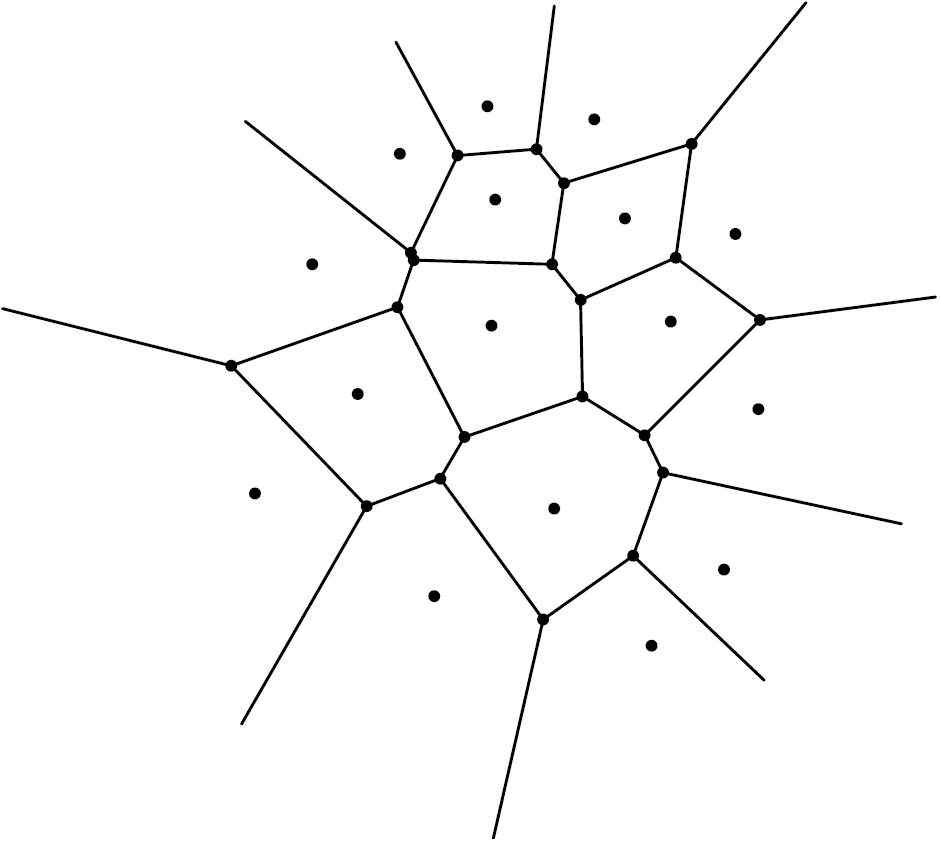
Il existe une autre façon de découper le plan en régions. C’est le diagramme de Voronoï de l’ensemble des centres des disques. Considérons un ensemble ![]() de points du plan. Le diagramme de Voronoï de
de points du plan. Le diagramme de Voronoï de ![]() est la partition du plan en régions, chaque point
est la partition du plan en régions, chaque point ![]() de
de ![]() correspondant à une région, de sorte que la région attachée à un point
correspondant à une région, de sorte que la région attachée à un point ![]() donné est l’ensemble des points du plan qui sont plus proches de
donné est l’ensemble des points du plan qui sont plus proches de ![]() que de n’importe quel autre point
que de n’importe quel autre point ![]() de
de ![]() . Ces régions sont appelées cellules de Voronoï. Étant donné que la médiatrice d’un segment
. Ces régions sont appelées cellules de Voronoï. Étant donné que la médiatrice d’un segment ![]() est le lieu géométrique des points équidistants de
est le lieu géométrique des points équidistants de ![]() et de
et de ![]() , il n’est pas surprenant que le diagramme de Voronoï d’un ensemble de points ressemble à la Figure 5, où le coté commun entre deux cellules de Voronoï est un segment de la médiatrice des deux points de
, il n’est pas surprenant que le diagramme de Voronoï d’un ensemble de points ressemble à la Figure 5, où le coté commun entre deux cellules de Voronoï est un segment de la médiatrice des deux points de ![]() associés aux deux cellules.
associés aux deux cellules.
Lorsque l’on a un empilement de disques dans le plan, il est naturel de regarder le diagramme de Voronoï de l’ensemble des centres des disques. Regardons à nouveau les deux exemples de la Figure 2. A gauche, les cellules de Voronoï sont des carrés. A droite ce sont des hexagones, et la densité de chaque disque dans sa cellule de Voronoï est exactement ![]() . Remarquons que si on entoure un disque donné par des disques de même rayon, sans chevauchement, la cellule de Voronoï d’aire minimale est l’hexagone circonscrit.
. Remarquons que si on entoure un disque donné par des disques de même rayon, sans chevauchement, la cellule de Voronoï d’aire minimale est l’hexagone circonscrit.
3. En dimension ![]() .
.
3.1. La difficulté du problème.
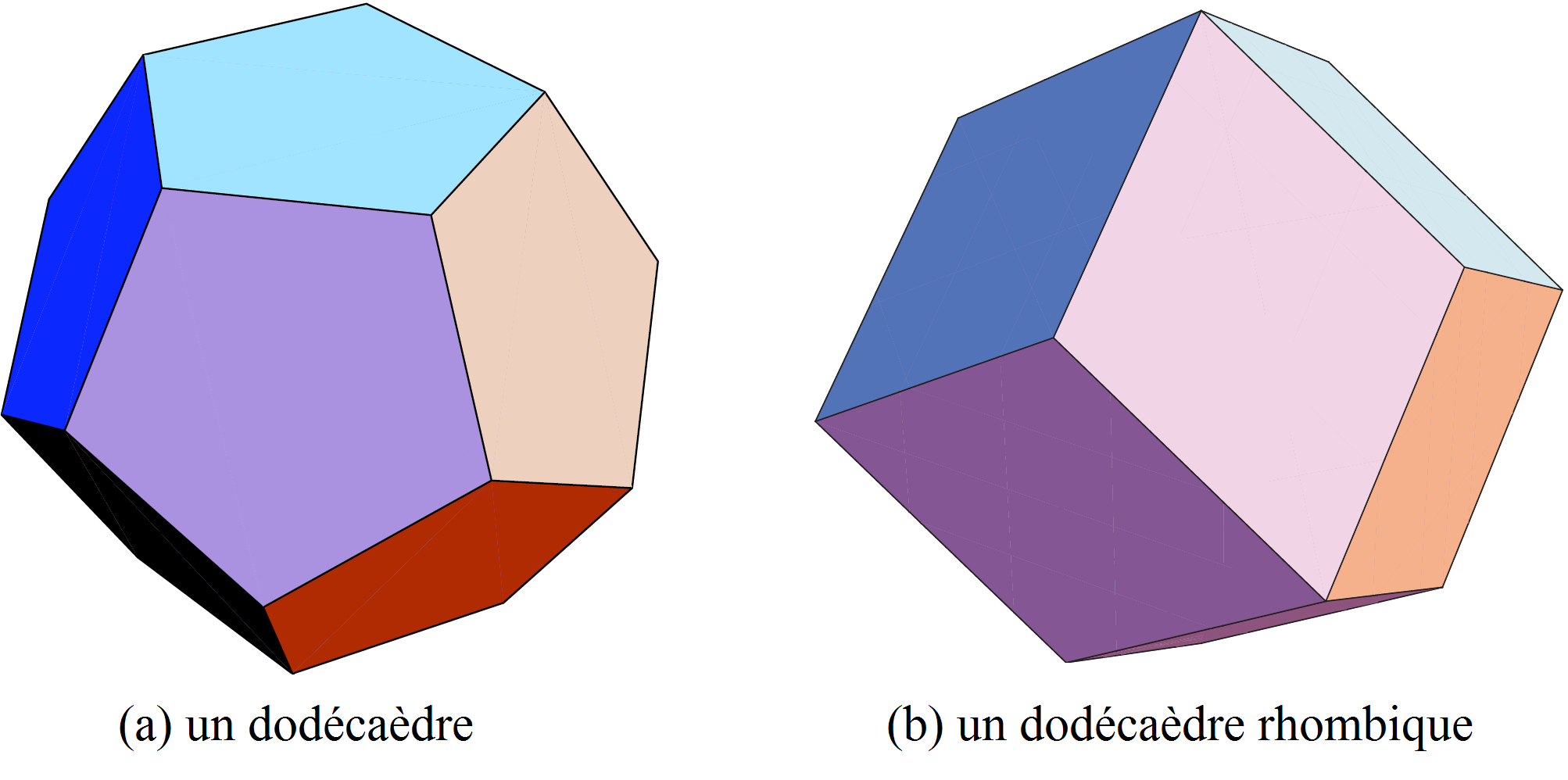
Il est naturel d’essayer de généraliser cette idée au cas tridimensionnel. Le diagramme de Voronoï peut être défini comme précédemment. Ses cellules fermées sont des polyèdres convexes. Entourons une sphère par des sphères tangentes. On peut en positionner ![]() . Mais contrairement au cas en dimension
. Mais contrairement au cas en dimension ![]() , il reste de l’espace autour de la sphère originale. On peut essayer de déplacer les
, il reste de l’espace autour de la sphère originale. On peut essayer de déplacer les ![]() sphères tangentes, et voir si on pourrait en placer une 13-ième. Il a été prouvé par Thomas Hales que ce n’est pas possible. Mais il existe de nombreuse façons non équivalentes de placer
sphères tangentes, et voir si on pourrait en placer une 13-ième. Il a été prouvé par Thomas Hales que ce n’est pas possible. Mais il existe de nombreuse façons non équivalentes de placer ![]() sphères tangentes à une sphère donnée, et elles ne produisent pas des cellules de Voronoï de même volume! La configuration optimale pour minimiser le volume de la cellule de Voronoï consiste à faire en sorte que les
sphères tangentes à une sphère donnée, et elles ne produisent pas des cellules de Voronoï de même volume! La configuration optimale pour minimiser le volume de la cellule de Voronoï consiste à faire en sorte que les ![]() sphères tangentes à la sphère originale soient tangentes à celle-ci aux sommets de son dodécaèdre inscrit (Figure 6 (a)). Ceci a été conjecturé par Fejer Tóth dans les années 1940 et finalement démontré par un étudiant de licence, Sean McLaughlin, en 1999!
sphères tangentes à la sphère originale soient tangentes à celle-ci aux sommets de son dodécaèdre inscrit (Figure 6 (a)). Ceci a été conjecturé par Fejer Tóth dans les années 1940 et finalement démontré par un étudiant de licence, Sean McLaughlin, en 1999!
La cellule de Voronoï de la sphère est alors un dodécaèdre circonscrit à la sphère. Il est possible de calculer la densité de la sphère dans sa cellule de Voronoï.
Elle est inférieure à la densité de l’empilement d’orange des étales de fruits ! Peut-on trouver mieux ?
Non!
Pourquoi? Parce qu’il est impossible de remplir l’espace avec des dodécaèdres qui ne se recouvrent pas au moins partiellement : on aura nécessairement des espaces vides entre eux. Par conséquent, le cas tridimensionnel est bien plus difficile que le cas bidimensionnel, puisque la solution optimale locale ne coïncide pas avec la solution optimale globale.
Pour la solution optimale dont nous étudierons la géométrie dans la prochaine section, il faut placer les centres des sphères aux points d’un système cristallin cubique. Les cellules de Voronoï correspondantes sont des dodécaèdres rhombiques (voir Figure 6 (b)).
Les dodécaèdres rhombiques peuvent paver l’espace de façon régulière, et de tels pavages ont été observés en cristallographie.
La preuve de l’optimalité de cet empilement a été terminée par Thomas Hales avec l’aide de son étudiant Samuel Ferguson en 1998 (la preuve complète a seulement été publiée en 2006). La preuve, assistée par ordinateur, est réellement un tour de force. Bien qu’on ne puisse pas imiter la preuve du cas bidimensionnel, l’esprit demeure le même : la preuve consiste à découper l’espace en régions, tout en ayant seulement un nombre fini de types de régions, et de calculer la densité dans chaque type de région. Le programme (colossal) est disponible sur internet pour ceux qui voudraient l’étudier ou le vérifier.
3.2. La géométrie de l’empilement optimal.
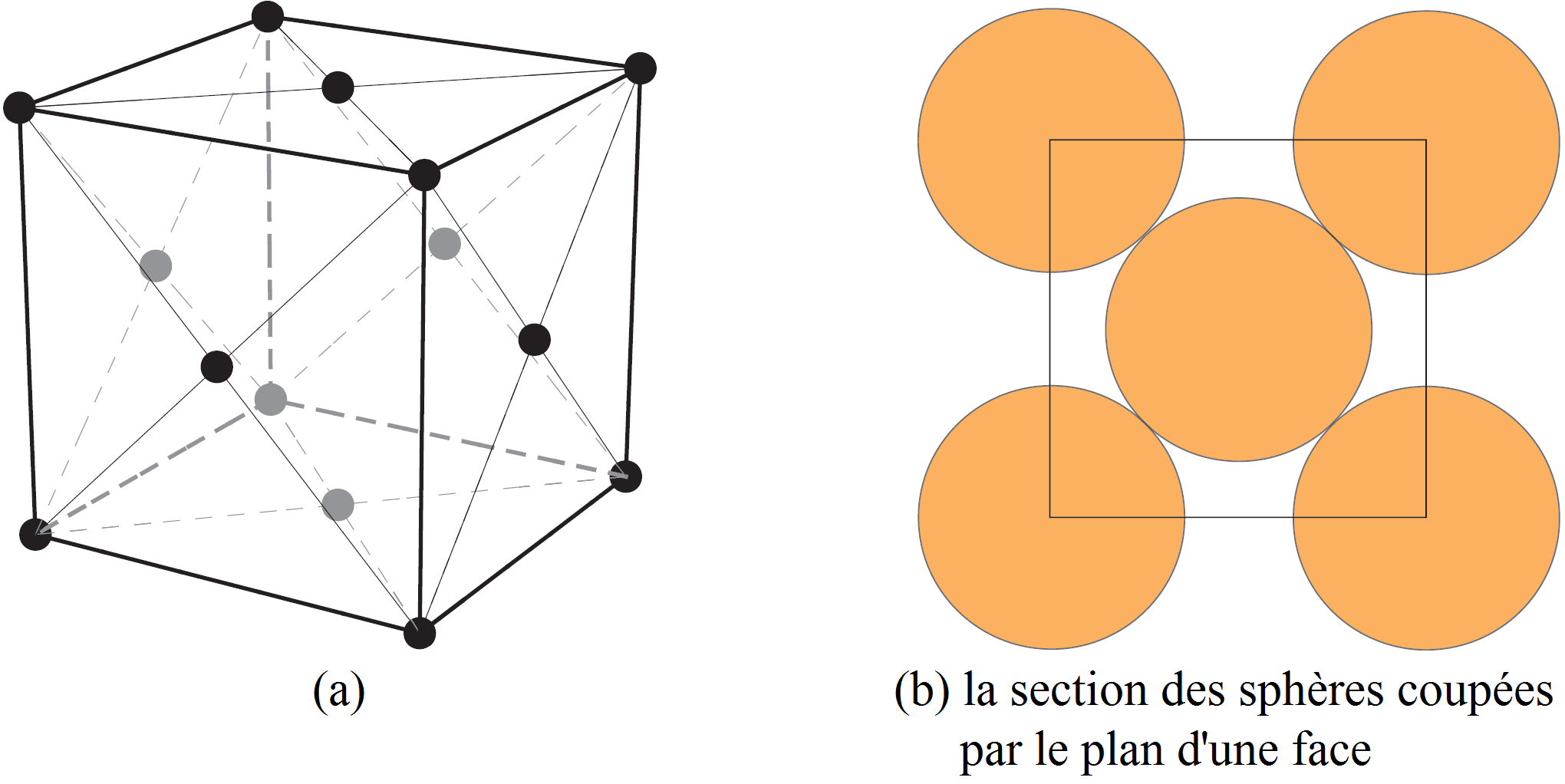
Imaginez un pavage de l’espace tridimensionnel avec des cubes. On place des sphères dont les centres sont chacun des sommets de chaque cube, et sur chaque face de chaque cube on place une sphère dont le centre est le centre de la face, comme suit :
Nous choisissons le rayon des sphères aussi large que possible de sorte que les sphères ne s’intersectent pas. Si ![]() est la longueur d’une arête du cube, alors il est clair d’après la Figure 7 (b) que le rayon des sphères doit être
est la longueur d’une arête du cube, alors il est clair d’après la Figure 7 (b) que le rayon des sphères doit être ![]() . Nous pouvons donc calculer la densité de l’empilement. En effet, pour chaque sphère centrée sur un sommet, un huitième de la sphère est contenue dans le cube. Puisqu’il y a huit sommets, on obtient par addition le volume d’une sphère. Pour chaque sphère dont le centre est le centre d’une face du cube, la moitié de son volume est contenu à l’intérieur du cube. Puisqu’il y a six faces, on obtient par addition le volume de trois sphères. Par conséquent la densité est le volume de quatre sphères divisé par le volume du cube. Le volume de chaque sphère est
. Nous pouvons donc calculer la densité de l’empilement. En effet, pour chaque sphère centrée sur un sommet, un huitième de la sphère est contenue dans le cube. Puisqu’il y a huit sommets, on obtient par addition le volume d’une sphère. Pour chaque sphère dont le centre est le centre d’une face du cube, la moitié de son volume est contenu à l’intérieur du cube. Puisqu’il y a six faces, on obtient par addition le volume de trois sphères. Par conséquent la densité est le volume de quatre sphères divisé par le volume du cube. Le volume de chaque sphère est ![]() et le volume du cube est
et le volume du cube est ![]() . Ainsi la densité est
. Ainsi la densité est
![]()
Comment réaliser cet empilement ? Comme lorsque l’on empile des oranges : on place d’abord une couche plane de sphères comme dans la Figure 2 (b). Par-dessus, on place une seconde couche avec un décalage, dans notre cas vers le haut à droite. La troisième couche repose par-dessus la seconde avec encore un décalage identique, etc. Ceci nous amène à une question : Peut-on changer la direction des décalages entre différentes couches sans changer la densité ? Oui, on peut, mais le réseau des centres des sphères ne sera alors pas le système cristallin cubique. Ceci signifie que l’empilement donnant la densité la plus élevée n’est pas unique.
Il n’est pas évident que l’empilement classique d’oranges corresponde au système cristallin cubique. En effet, si on regarde la Figure 7 (b), on voit que l’on devrait avoir des droites orthogonales sur lesquelles se situent les centres des sphères alignées. Se rendre compte que ces droites existent dans l’empilement classique d’oranges, mais qu’aucune n’est horizontale, est un bon exercice de visualisation. En effet, le plan de la Figure 2 (b) est un plan incliné passant par les centres de trois faces adjacentes à un sommet du cube de la Figure 7 (a). Dans la Figure 8, on représente l’empilement de quatre couches comme celle de la Figure 2 (b), les unes au-dessus des autres. Les deux droites passant par les centres des sphères sont orthogonales.
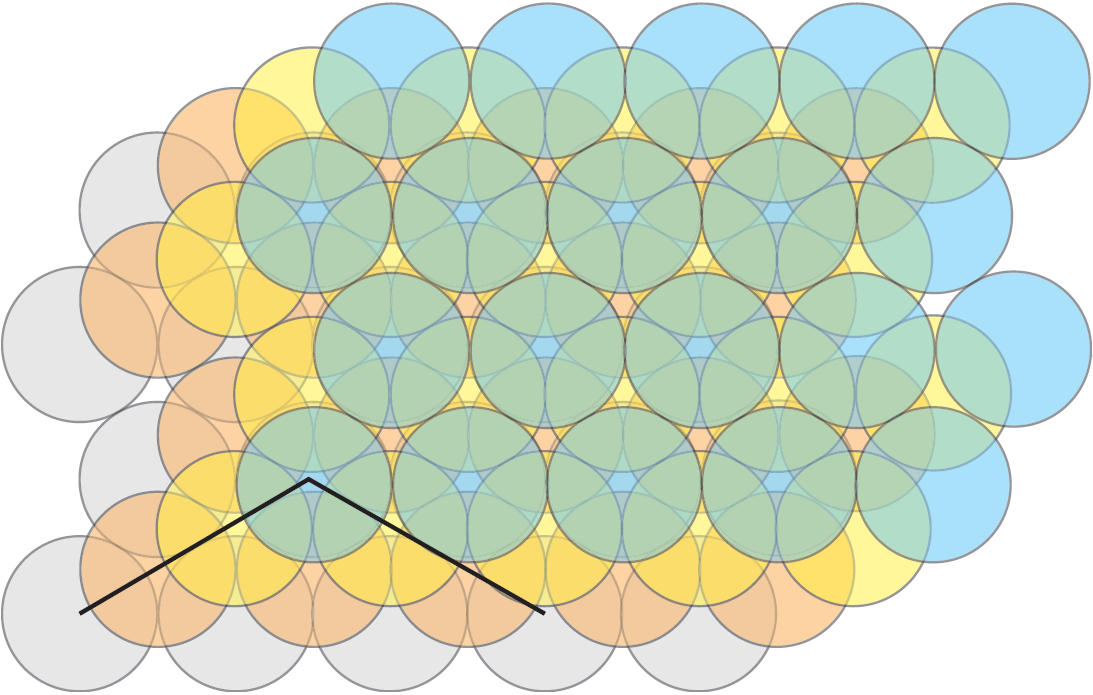
Figure 8: Quatre couches de sphères du type de la Figure 2 (b), les unes au-dessus des autres, et deux droites orthogonales passant par les centres de sphères alignées.
4. Vers d’autres horizons.
4.1. Applications en cristallographie.
La question de l’empilement de sphères le plus dense a été posée à Johannes Kepler par Thomas Harriot à la fin du 16-ième siècle. A l’époque, Harriot croyait déjà à l’existence des atomes et était intéressé à leur disposition les uns par rapport aux autres. Lorsque l’arrangement des atomes d’un matériau est régulier, les chimistes disent que ce matériau est un cristal. Des matériaux lourds, comme les métaux, ont souvent des atomes arrangés selon l’empilement cubique à faces centrées. D’autres arrangements moins denses existent aussi. L’un des empilements réguliers les moins denses est le simple empilement cubique où les atomes sont situés aux sommets de cubes. Il n’y a qu’un seul élément chimique avec cette configuration d’atomes, à savoir le polonium radioactif. (voir [4] pour plus de détails.)
4.2. Empilement aléatoire.
Si vous empilez avec soin vos oranges dans de grandes caisses en utilisant l’empilement cubique à faces centrées décrit ci-dessus, alors vous obtiendrez une densité ![]() Mais si vous êtes pressé et jetez rapidement les oranges dans la caisse, quelle densité obtiendrez-vous ? C’est ce que l’on appelle l’empilement aléatoire. Bien sûr, la densité ne sera jamais la même. En effet, si vous secouez votre caisse, vous allez certainement augmenter la densité. Mais jusqu’à quel point ? Les expériences montrent que la densité varie d’environ
Mais si vous êtes pressé et jetez rapidement les oranges dans la caisse, quelle densité obtiendrez-vous ? C’est ce que l’on appelle l’empilement aléatoire. Bien sûr, la densité ne sera jamais la même. En effet, si vous secouez votre caisse, vous allez certainement augmenter la densité. Mais jusqu’à quel point ? Les expériences montrent que la densité varie d’environ ![]() (empilement aléatoire lâche) à un maximum de
(empilement aléatoire lâche) à un maximum de ![]() (empilement aléatoire compact). La dérivation de cette limite maximum était le sujet d’un article de Nature en 2008 par Song, Wang et Maske [3].
(empilement aléatoire compact). La dérivation de cette limite maximum était le sujet d’un article de Nature en 2008 par Song, Wang et Maske [3].
4.3. Empiler d’autres objets que des sphères.
Est-ce possible d’obtenir une densité supérieure à ![]() si au lieu d’utiliser des sphères on utilisait, par exemple, des ellipses ? L’article [1] montre que la densité de l’empilement aléatoire compact de sphéroïdes, comme les bonbons M & M, peut s’approcher de
si au lieu d’utiliser des sphères on utilisait, par exemple, des ellipses ? L’article [1] montre que la densité de l’empilement aléatoire compact de sphéroïdes, comme les bonbons M & M, peut s’approcher de ![]() à
à ![]() et que la densité pour certains ellipsoïdes, avec d’autres rapports entre les longueurs des axes de l’ellipse, peut même approcher
et que la densité pour certains ellipsoïdes, avec d’autres rapports entre les longueurs des axes de l’ellipse, peut même approcher ![]() . Les densités des empilements aléatoires sont importantes pour l’industrie lorsque l’emballage de produits identiques (des bonbons ou des pilules par exemple) est automatique. En particulier, la densité peut changer pendant le transport.
. Les densités des empilements aléatoires sont importantes pour l’industrie lorsque l’emballage de produits identiques (des bonbons ou des pilules par exemple) est automatique. En particulier, la densité peut changer pendant le transport.
4.4. Un mot sur les dimensions supérieures…
En dimension supérieure, les empilements réguliers les plus denses d’hypersphères sont connus jusqu’à la dimension ![]() , et nous ne savons que très peu de chose sur les empilements non réguliers.
, et nous ne savons que très peu de chose sur les empilements non réguliers.
Une application de l’empilement de sphères en dimension supérieure est la création de codes correcteurs. Le principe d’un code correcteur est d’encoder des lettres par des suites de symboles, appelées mots de code , qui diffèrent les uns des autres par au moins ![]() symboles. Ensuite, si moins de
symboles. Ensuite, si moins de ![]() erreurs apparaissent lors de la transmission d’un mot de code, il existe au plus un mot de code se trouvant à une distance inférieure à
erreurs apparaissent lors de la transmission d’un mot de code, il existe au plus un mot de code se trouvant à une distance inférieure à ![]() du mot reçu, et la correction est possible. Les codes correcteurs utilisant des empilements de sphères transforment les lettres du mot en des coordonnées de centres de sphères ne se chevauchant pas. Si les sphères ont un rayon
du mot reçu, et la correction est possible. Les codes correcteurs utilisant des empilements de sphères transforment les lettres du mot en des coordonnées de centres de sphères ne se chevauchant pas. Si les sphères ont un rayon ![]() , alors il est possible de corriger moins de
, alors il est possible de corriger moins de ![]() erreurs.
erreurs.
4.5. Les questions suivantes…
C’est à votre tour de les poser. Comme vous l’avez vu, il existe de nombreuses questions simples possédant des applications importantes, et dont les réponses sophistiquées sont publiées dans certains des journaux scientifiques les plus importants, comme Nature, Science, et Annals of Mathematics.
5. La validité des preuves assistées par ordinateur.
La preuve que la densité de l’empilement de disques le plus dense dans le cas bidimensionnel est ![]() montre qu’il est possible de donner des preuves rigoureuses de résultats où il y a un nombre infini de cas à analyser. C’est une preuve que chacun d’entre vous peut vérifier. Mais qui peut vérifier la preuve de
montre qu’il est possible de donner des preuves rigoureuses de résultats où il y a un nombre infini de cas à analyser. C’est une preuve que chacun d’entre vous peut vérifier. Mais qui peut vérifier la preuve de ![]() ? Il s’agit d’une preuve énorme avec
? Il s’agit d’une preuve énorme avec ![]() cas à analyser, et chaque cas est si complexe qu’il doit être fait par un ordinateur, pour un total de 3 Gigabytes de codes informatiques. Bien sûr, le code est public. Mais ses auteurs ont eu besoin de plusieurs années pour le construire. Qui donc a suffisamment de temps et de talent pour vérifier tous les détails ? Bien sûr, il existe des stratégies pour minimiser les erreurs, et Hales et Solomon en ont utilisé plusieurs. Par exemple, les auteurs ont écrit le programme indépendamment en parallèle. Le programme pourrait être exécuté sur des ordinateurs différents avec des processeurs et des compilateurs différents. Les sous-routines pourraient utiliser des modules plus anciens ayant été testés durant des années, etc.
cas à analyser, et chaque cas est si complexe qu’il doit être fait par un ordinateur, pour un total de 3 Gigabytes de codes informatiques. Bien sûr, le code est public. Mais ses auteurs ont eu besoin de plusieurs années pour le construire. Qui donc a suffisamment de temps et de talent pour vérifier tous les détails ? Bien sûr, il existe des stratégies pour minimiser les erreurs, et Hales et Solomon en ont utilisé plusieurs. Par exemple, les auteurs ont écrit le programme indépendamment en parallèle. Le programme pourrait être exécuté sur des ordinateurs différents avec des processeurs et des compilateurs différents. Les sous-routines pourraient utiliser des modules plus anciens ayant été testés durant des années, etc.
Pourtant ces preuves restent controversées, et la communauté scientifique n’a accepté une telle preuve qu’après un processus de décision très long. Dans le cas de la preuve de la conjecture de Kepler, la preuve (abrégée) n’est finalement apparue qu’en 2005 dans les Annals of Mathematics, l’un des meilleurs journaux mathématiques. Mais la communauté mathématiques est toujours à la recherche d’une preuve plus “mathématique”. En parallèle, des mathématiciens et des chercheurs en informatique théorique recherchent des preuves formelles, i.e. des preuves dans lesquelles chaque étape logique peut être vérifiée par un ordinateur. Par exemple, l’objectif du projet Flyspeck est de construire une preuve formelle de la conjecture de Kepler :
http://code.google.com/p/flyspeck/wiki/FlyspeckFactSheet
Le premier grand théorème dont la preuve a été assistée par ordinateur est le théorème des quatre couleurs qui affirme que quatre couleurs suffisent pour colorier n’importe quelle carte sans que deux régions voisines ne soient de la même couleur. Il a été démontré en 1976 par Kenneth Appel et Wolfgang Haken. A l’époque, les Annals of Mathematics n’auraient pas accepté la preuve assistée par ordinateur. Les temps ont changé, et l’ordinateur a révolutionné la pratique des mathématiques.
Références.
[1] A. Donev, I. Cisse, D. Sachs, E. Variano, F. H. Stillinger, R. Connelly, S. Tarquato et P.M. Chikin, Improving the density of jammed disordered packings using ellipsoids, Science, 303 (2004), 990–993.
[2] T. Hales, Cannonballs and honeycombs, Notices of the American Mathematical Society, 47 (2000), 440–449.
[3] C. Song, P. Wang et H.A. Maske, A phase diagram for jammed matter, Nature, 453 (2008), 629–-632.
[4] G.C. Szpiro, Kepler’s conjecture, John Wiley & Sons, Inc., 2003.
Ce post est disponible en: Anglais, Allemand, Italien, Espagnol, Arabe, Khmère

 Français
Français 简体中文
简体中文  English
English  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português
super article mais j’ai pas compris pourquoi dans la partie 1 sur les cercle le secteur (a) fait (3/4)=(1/c²)de densité vous fixer “c” de cette manière ? mais ducoup sa nuit pas a la démonstration ?