
Figure 1: Illustration d'une variété de Calabi-Yau (Importante pour la description des modèles de dimension supérieures en théorie des supercordes).
1. A la recherche de la prochaine dimension
Notre monde a-t-il réellement plus de trois dimensions? Dans ce cas, les objets de dimensions supérieures ont-ils un lien avec le monde qui nous entoure? Est-il possible de percevoir ces objets ou échappent-ils à toute représentation? La théorie de la relativité utilise quatre dimensions pour expliquer le concept d’espace-temps, six dimensions sont nécessaires pour décrire la courbure de l’espace-temps et les différentes théories des cordes utilisent même des espaces à
Ces exemples montrent l’une des caractéristiques principales de la pensée mathématiques: S’il est plus facile ou plus pratique de décrire un phénomène dans un espace de dimension supérieure , l’espace à trois dimensions peut être étendu. Ceci peut aisément être expliqué sous des aspects formels. Ainsi des équations linéaires avec trois variables peuvent être vues comme des plans dans l’espace, des équations linéaires à quatre dimensions peuvent être interprétées comme des hyperplans d’un espace à quatre dimensions. Ainsi, des équations linéaires à ![]() variables peuvent être interprétées comme un hyperplan d’un espace à
variables peuvent être interprétées comme un hyperplan d’un espace à ![]() dimensions. En utilisant plus de trois variables, l’avantage d’une telle extension du concept de dimension provient d’une description plus simple et régulière des relations mathématiques. Il n’est pas nécessaire pour les calculs formels sur un niveau algébrique ou numérique d’avoir des illustrations dans un contexte de dimensions supérieures. Néanmoins, ceci nous conduit à poser la question de l’interprétation de tels résultats dans le monde réel. D’un autre coté, on a besoin de décrire au moins les objets basiques des dimensions supérieures dans notre espace à trois dimensions.
dimensions. En utilisant plus de trois variables, l’avantage d’une telle extension du concept de dimension provient d’une description plus simple et régulière des relations mathématiques. Il n’est pas nécessaire pour les calculs formels sur un niveau algébrique ou numérique d’avoir des illustrations dans un contexte de dimensions supérieures. Néanmoins, ceci nous conduit à poser la question de l’interprétation de tels résultats dans le monde réel. D’un autre coté, on a besoin de décrire au moins les objets basiques des dimensions supérieures dans notre espace à trois dimensions.
Dans ce qui suit, le développement des représentations des objets de dimensions supérieures seront traitées en discutant de l’exemple du cube à quatre dimensions. On démontrera que l’approche du cube à quatre dimensions – ou plus – peut être faite de plusieurs façons. Dans ce qui suit, trois approches différentes seront abordées et analysées (une description détaillée de ces approches est disponible dans [9]).
(1) Projections d’objets de dimensions supérieures sur des (hyper)plans,
(2) Intersections de (hyper)cubes et de (hyper)plans,
(3) Une extension systématique du concept de coordonnées.
2. Projections
Dans ce paragraphe, l’idée basique de décrire des objets de dimensions supérieures par le biais de projections sera généralisé aux dimensions supérieures. En particulier la projection orthogonale le long d’une grande diagonale d’un hypercube à ![]() dimensions dans un espace à
dimensions dans un espace à ![]() dimensions peut être généralisée facilement.
dimensions peut être généralisée facilement.
Exemple 1: Projections du carré et du cube
Figure 2.1: Projection d’un cube. Auteur: Sebastian Hammer, Université de Würzburg.
Figure 2.2: Projection d’un cube. Auteur: Sebastian Hammer, Université de Würzburg.
Pour ![]() soit
soit ![]() un sommet du carré. La projection de la Figure 2.1 est représentée par l’intersection des droites
un sommet du carré. La projection de la Figure 2.1 est représentée par l’intersection des droites
![]() , (
, (![]() )
)
avec la droite
![]() .
.
C’est une projection orthogonale. De même, la projection orthogonale d’un hypercube à ![]() -dimensions est entièrement décrite par la projection des coordonnées des sommets. On s’intéresse aux intersections des droites:
-dimensions est entièrement décrite par la projection des coordonnées des sommets. On s’intéresse aux intersections des droites:
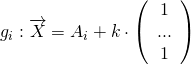 , (
, (![]() )
)
et de l’hyperplan
![]() .
.
Le vecteur ![]() est orthogonal à l’hyperplan
est orthogonal à l’hyperplan ![]() , les droites
, les droites ![]() sont orthogonales à l’hyperplan
sont orthogonales à l’hyperplan ![]() aux points
aux points ![]() . En considérant les similarités des projections ci-dessus, comme les sommets ayant les mêmes images par ces transformations, on obtient la Figure 3.2 comme représentation pour la projection orthogonale correspondante d’un hypercube de dimension
. En considérant les similarités des projections ci-dessus, comme les sommets ayant les mêmes images par ces transformations, on obtient la Figure 3.2 comme représentation pour la projection orthogonale correspondante d’un hypercube de dimension ![]() dans l’espace de dimension
dans l’espace de dimension ![]() .
.
Une autre possibilité pour décrire des projections orthogonales d’espaces de dimension ![]() dans des espaces de dimension
dans des espaces de dimension ![]() (
(![]() ) utilise la linéarité des projections orthogonales (en tant que transformations linéaires). Cette propriété peut être utilisée pour créer et comprendre des images bidimensionnelles de cubes de n’importe quelle dimension.
) utilise la linéarité des projections orthogonales (en tant que transformations linéaires). Cette propriété peut être utilisée pour créer et comprendre des images bidimensionnelles de cubes de n’importe quelle dimension.

Figure 3.1: Projection d'un hypercube de dimension 4; Huit des arêtes sont projetées sur les sommets d'un cube de dimension 3.
Figure 3.2: Projection d'un hypercube de dimension 4; modèle virtuel.
Exemple 2: Projection d’un hypercube
La Figure 2.2 montre trois vecteurs qui engendrent un cube et leurs images par projection orthogonale le long d’un grande diagonale. Tous les sommets du cube sont des combinaisons linéaires de ces vecteurs avec des coefficients ![]() et
et ![]() . La linéarité de la projection mène à la même propriété pour les images de tous les sommets.
. La linéarité de la projection mène à la même propriété pour les images de tous les sommets.
En décrivant le cube de dimension ![]() avec les combinaisons linéaires adéquates de
avec les combinaisons linéaires adéquates de ![]() vecteurs générateurs indépendants, on peut démontrer la chose suivante: Pour le cube de dimension
vecteurs générateurs indépendants, on peut démontrer la chose suivante: Pour le cube de dimension ![]() , il existe une projection orthogonale dans
, il existe une projection orthogonale dans ![]() et un plan de projection approprié, de sorte que les images des vecteurs générateurs soient les sommets d’un polygone régulier à
et un plan de projection approprié, de sorte que les images des vecteurs générateurs soient les sommets d’un polygone régulier à ![]() cotés. Par additivité, les images des autres sommets sont les combinaisons linéaires correspondantes. (Pour
cotés. Par additivité, les images des autres sommets sont les combinaisons linéaires correspondantes. (Pour ![]() voir la Figure 2.2 et l’exemple 1, avec le triangle régulier comme image des vecteurs générateurs).
voir la Figure 2.2 et l’exemple 1, avec le triangle régulier comme image des vecteurs générateurs).
Pour comprendre comment la projection d’un hypercube de dimension ![]() dans un sous espace de dimension
dans un sous espace de dimension ![]() est obtenue on explique d’abord comment un cube est projeté sur une droite de l’espace à trois dimensions:
est obtenue on explique d’abord comment un cube est projeté sur une droite de l’espace à trois dimensions:
Pour chaque sommet du cube, prendre le plan orthogonal à la droite donnée qui contient ce sommet. Le point d’intersection du plan et de la droite est la projection orthogonale du sommet sur cette droite.
De façon similaire, on projette l’hypercube de dimension ![]() dans le sous espace de dimension
dans le sous espace de dimension ![]() . Pour chaque sommet de l’hypercube, prendre l’espace de dimension
. Pour chaque sommet de l’hypercube, prendre l’espace de dimension ![]() orthogonal au sous espace de dimension
orthogonal au sous espace de dimension ![]() qui contient ce sommet. L’intersection de ces deux sous espaces est la projection orthogonale du sommet dans le sous espace de dimension
qui contient ce sommet. L’intersection de ces deux sous espaces est la projection orthogonale du sommet dans le sous espace de dimension ![]() .
.
Ainsi, une projection en dimension deux d’un cube de dimension cinq peut être construit: En se basant sur les images des vecteurs générateurs (qui donnent les sommets d’un pentagone régulier), l’image de n’importe quel sommet peut être construite en additionnant les vecteurs appropriés (voir la Figure 4.1).
En regardant la projection du cube de dimension cinq, on remarque que les images des arêtes du cube engendrent le losange de Penrose (voir Senechal 1995). Un autre phénomène remarquable est visible sur la Figure 4.2. La projection d’un hypercube de dimension six le long d’une grande diagonale – le segment d’extrémités ![]() et
et ![]() – donne à plusieurs sommets la même image. Le nombre d’antécédents est aussi donné dans la Figure 4.2.
– donne à plusieurs sommets la même image. Le nombre d’antécédents est aussi donné dans la Figure 4.2.

Figure 4.1: Une projection d'un cube de dimension cinq dans un plan.
Figure 4.2: Une projection d'un cube de dimension six dans un plan.
3. Intersections de cubes
Une représentation dynamique d’un hypercube de dimension quatre peut être obtenue en considérant les différentes formes de ses intersections avec un hyperplan. Tout d’abord, on observera l’interaction d’un cube (en dimension trois), avec un plan. On admettra que ces objets se déplacent avec une vitesse (relative) ![]() . Il est particulièrement facile de décrire la situation en considérant un cube (dont la longueur des cotés est
. Il est particulièrement facile de décrire la situation en considérant un cube (dont la longueur des cotés est ![]() ) dont les arêtes sont situées sur les axes d’un repère. Le plan
) dont les arêtes sont situées sur les axes d’un repère. Le plan ![]() se déplace à l’intérieur du cube, le long d’une diagonale, avec une vitesse
se déplace à l’intérieur du cube, le long d’une diagonale, avec une vitesse ![]() . Puisque le cube est convexe, il suffit de déterminer les points d’intersection avec les arêtes. La section est alors l’enveloppe convexe de ces points.
. Puisque le cube est convexe, il suffit de déterminer les points d’intersection avec les arêtes. La section est alors l’enveloppe convexe de ces points.
L’intersection d’un espace tridimensionnel se déplaçant à travers un hypercube de dimension quatre sera représenté de façon analogue:
Un hypercube de dimension quatre avec des arêtes de longueur ![]() sera intersecté par un espace
sera intersecté par un espace ![]() , se déplaçant à une vitesse
, se déplaçant à une vitesse ![]() le long d’une diagonale de l’hypercube. On définit donc de même:
le long d’une diagonale de l’hypercube. On définit donc de même:
![]() .
.
Cette fois encore, il suffit de connaître les points d’intersection de l’hypercube avec ![]() .
.
Une simulation interactive de ces intersections en dimension ![]() à
à ![]() est disponible dans l’applet suivant (Auteur: Rafael Losada, Instituto GeoGebra de Cantabria).
est disponible dans l’applet suivant (Auteur: Rafael Losada, Instituto GeoGebra de Cantabria).
4. La géométrie des coordonnées
Le segment de longueur ![]() ou le carré de coté
ou le carré de coté ![]() , peuvent être considérés comme des analogues uni- et bidimensionnels du cube unité. En étudiant les coordonnées de leurs sommets, on obtient les sommets du
, peuvent être considérés comme des analogues uni- et bidimensionnels du cube unité. En étudiant les coordonnées de leurs sommets, on obtient les sommets du
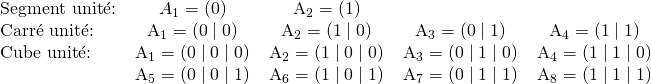
En ajoutant successivement des coordonnées supplémentaires avec les coefficients ![]() et
et ![]() , les coordonnées des sommets, et donc le nombre de sommets, d’un hypercube dans un système à quatre – ou cinq – dimensions, peuvent être obtenus. La transition vers les hypercubes de dimensions supérieures peut exclusivement être obtenues au niveau symbolique et peut être considérée comme une extension du concept de coordonnées. Des notions combinatoires nous mènent à la relation suivante entre le nombre
, les coordonnées des sommets, et donc le nombre de sommets, d’un hypercube dans un système à quatre – ou cinq – dimensions, peuvent être obtenus. La transition vers les hypercubes de dimensions supérieures peut exclusivement être obtenues au niveau symbolique et peut être considérée comme une extension du concept de coordonnées. Des notions combinatoires nous mènent à la relation suivante entre le nombre ![]() de “cubes frontière” (i.e. cubes délimitant) de dimension
de “cubes frontière” (i.e. cubes délimitant) de dimension ![]() d’un cube de dimension
d’un cube de dimension ![]() (voir e. g. Graumann, 2009):
(voir e. g. Graumann, 2009):
![]()
Cette formule se déduit des observations suivantes:
- Chaque “cube frontière” de dimension
 est parallèle à un sous espace de dimension
est parallèle à un sous espace de dimension  qui est engendré par
qui est engendré par 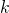 vecteurs du cube de dimension
vecteurs du cube de dimension 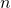 (voir sec. 3). Par conséquent, les coordonnées des sommets d’un “cube frontière” diffèrent par au plus
(voir sec. 3). Par conséquent, les coordonnées des sommets d’un “cube frontière” diffèrent par au plus 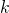 coefficients.
coefficients. - Il y a
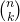 possibilités pour choisir
possibilités pour choisir 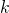 coefficients parmi
coefficients parmi 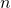 .
. - Il y a
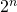 possibilités pour choisir un “sommet de départ”.
possibilités pour choisir un “sommet de départ”. - Il y a
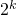 sommets de départ menant au même cube frontière.
sommets de départ menant au même cube frontière.
Exemple 3: Le cube tridimensionnel (![]() ):
):
Nombre de sommets (![]() ):
): ![]()
Nombre d’arêtes (![]() ):
): ![]()
Nombres de faces (![]() ):
): ![]()
Nombre de cubes (![]() ):
): ![]()
Ceci est visible dans le tableau interactif suivant: (Auteur: Markus Ruppert, Universität Würzburg).
Tout d’abord, en suivant les flèches jaunes, le tableau permet d’interpréter des points comme des cubes de dimension ![]() , de sorte que la formule ci-dessus reste exacte même pour
, de sorte que la formule ci-dessus reste exacte même pour ![]() . Les suites de nombres colorés d’une même couleur mènent vers de nouvelles conjectures, qui peuvent être démontrées en utilisant la formule définissant
. Les suites de nombres colorés d’une même couleur mènent vers de nouvelles conjectures, qui peuvent être démontrées en utilisant la formule définissant ![]() . Par exemple:
. Par exemple:
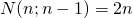 (couleur rouge)
(couleur rouge)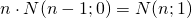 (couleur verte)
(couleur verte)- For all
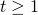 ,
, 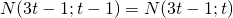 (couleur bleue)
(couleur bleue)
De plus, on obtient une formule de récurrence permettant d’obtenir des informations pour le cube de dimension ![]() à partir des informations des cubes de dimension
à partir des informations des cubes de dimension ![]()
Exemple 4: Preuve de la formule de récurrence
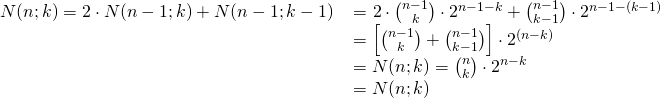
Bien sûr, ces arguments algébriques peuvent facilement être interprétés d’un point de vue géométrique.
5. Quasi-cristaux — Projections depuis les dimensions supérieures
En partant des éléments de cristallographie classique, à savoir la propriété des cristaux à être invariants selon trois translations indépendantes, les représentations mathématiques de ces structures nous mènent à la fameuse “restriction cristallographique”, qui n’autorise que des symétries par rotations non triviales d’ordres ![]() ,
, ![]() ,
, ![]() et
et ![]() . Ceci correspondait aux observations physiques, jusqu’à ce que Shechtman et al. (1984) découvrent une structure cristalline non périodique (non invariante par translation) dans un alliage Al-Mn, ayant des symétries par rotation d’ordre cinq. Les cristallographes appellent ces structures des quasi-cristaux. Pour être exact:
. Ceci correspondait aux observations physiques, jusqu’à ce que Shechtman et al. (1984) découvrent une structure cristalline non périodique (non invariante par translation) dans un alliage Al-Mn, ayant des symétries par rotation d’ordre cinq. Les cristallographes appellent ces structures des quasi-cristaux. Pour être exact:
Les quasi-cristaux sont des structures ordonnées mais non périodiques. Ils forment des motifs qui remplissent tout l’espace sans pour autant être invariants par translations.
Mais ces quasi-cristaux peuvent être très compliqués: La non-invariance par translation engendre un manque de règles pour expliquer comment le motif se développe dans une région lointaine de celle observée. Il y a ici un challenge pour le mathématicien. Une avancée majeure a été faite par l’observation de nombreux quasi-cristaux semblant apériodiques qui n’étaient que des projections de réseaux réguliers de dimensions supérieures. En effet, regardons un simple exemple…
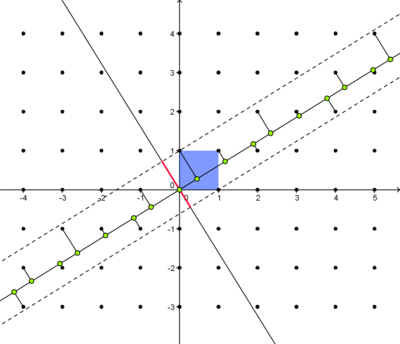
Exemple 5: Les quasi-cristaux unidimensionnels
Pour la droite ![]() dans
dans ![]() et son orthogonale
et son orthogonale ![]() à l’origine, avec
à l’origine, avec ![]() on considère la projection orthogonale du carré unité sur
on considère la projection orthogonale du carré unité sur ![]() (segment rouge). De plus on s’intéresse à chaque point de
(segment rouge). De plus on s’intéresse à chaque point de ![]() dont les images par cette projection sur cette droite sont dans ce segment rouge. Ces points sont maintenant projetés orthogonalement sur
dont les images par cette projection sur cette droite sont dans ce segment rouge. Ces points sont maintenant projetés orthogonalement sur ![]() (points verts).
(points verts).
La longueur des segments sur la droite de projection peuvent seulement prendre deux valeurs (correspondant aux projections des arêtes du carré unité). Ainsi on peut parler d’une “structure ordonnée”. En se déplaçant le long des droites, la suite de ces valeurs semble plus ou moins chaotique – il n’y a pas d’invariance par translation, mais si on observe ceci dans un univers à deux dimensions, alors tout devient clair: notre quasi-cristal est simplement une partie de la projection d’une grille régulière de carrés. Augmenter la dimension nous a permit de comprendre la structure cachée du quasi-cristal.
Ce procédé est assez général. Senechal (1995), par exemple, illustre les régularités et les hypothèses des méthodes de projection et de réseaux multiples qui mènent à des ensembles-points quasi-cristallins. En projetant, par exemple, des morceaux d’un réseau cubique de dimension cinq (![]() ) sur un certain plan, un ensemble de points, dans le sens décrit ci-dessus, est obtenu et peut être observé comme un quasi-cristal bidimensionnel. L’ensemble de points lui même montre tous les sommets du pavage du plan de Penrose (par les deux losanges caractéristiques, comparer au paragraphe 2 et à l’image 4.1).
) sur un certain plan, un ensemble de points, dans le sens décrit ci-dessus, est obtenu et peut être observé comme un quasi-cristal bidimensionnel. L’ensemble de points lui même montre tous les sommets du pavage du plan de Penrose (par les deux losanges caractéristiques, comparer au paragraphe 2 et à l’image 4.1).
Conclusion
Nous avons découvert une des façons de travailler des mathématiciens, qui est parfois résumée par la phrase suivante
Lorsque vous ne comprenez pas quelque chose, essayez de changer votre point de vue. Il se peut que cela vous donne une idée de la structure cachée. C’est ce que vous faites déjà lorsque essayez de comprendre une conique: vous choisissez un système de coordonnées approprié dans lequel l’équation est simple et révèle la structure de la conique.
Les bénéfices que les étudiants et élèves tireront du travail effectué en dimensions supérieures seront variés. En particulier, ils vont
- avoir un premier aperçu de la signification des dimensions supérieures en sciences;
- apprendre plusieurs façons d’approcher des objets en dimensions supérieures;
- utiliser les analogies pour étendre leur connaissance des trois dimensions classiques;
- utiliser les propriétés des objets de ce monde comme un concept abstrait d’un monde mental fictif;
- rafraîchir et répéter leur connaissances des projections des objets tridimensionnels dans le plan.
Références.
[1] BOTELHO, L.; BOTELHO, R.: Quantum Geometry of bosonic strings – Revisited. Notas de Física, Centro Brasileira de Pesquisas Físicas (1999).
[2] CAYLEY, A.: On Jacobi’s elliptic functions, in reply to the Rev..; and on quaternions. Philosophical Magazine. (1845) Nr. 26, S. 208–211.
[3] DELONE B.N., Geometry of positive quadratic forms, Usp. Mat. Nauk 3 (1937), S. 16‐62, und Usp. Mat. Nauk 4 (1938), S. 102‐164. (Russisch)
[4] GRAUMANN, G.: Spate in drei und mehr Dimensionen. MU 55/1 (2009), S. 16‐25
[5] HAMILTON, W. R.: On quaternions, or an new system of imagineries in algebra. Philosophical Magazine.(1844) Bd. 25(3), S. 489‐495.
[6] LAGARIAS, J.: Meyer’s concept of quasicrystal and quasiregular sets. Community of Mathematical Physics 179 (1996), S. 365‐376.
[7] MEYER, Y.: Algebraic numbers and harmonic analysis. North Holland (1972)
[8] RIEMANN, B.: Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe (Habil.). Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, Bd. 13 (1868)
[9] RUPPERT, M.: Würfelbetrachtungen. Drei Wege zu höheren Dimensionen. MU 56/1 (2010), S. 34‐53.
[10] SCHLÄFLI, L.: Theorie der vielfachen Kontinuität (1852). Denkschrift der Schweizerischen Naturforschenden Gesellschaft, Bd. 38, 1., Hrsg. Graf, J. H. (1901), S. 1‐237.
[11] SENECHAL, M.: Quasicrystals and geometry. Cambridge University Press (1995)
Le développement du concept de géométrie en dimension supérieure a commencé avec les travaux scientifiques de Hamilton (1844), Cayley (1845), Schläfli et Riemann.
Ce post est disponible en: Anglais, Allemand, Italien, Arabe, Khmère

 Français
Français 简体中文
简体中文  English
English  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português