CHRISTIAN MERCAT ET MICHÈLE ARTIGUE
Les frises et pavages accompagnent fréquemment l’enseignement des isométries. Les objets que nous allons considérer dans cette vignette, comme celui ci-dessous, n’en semblent pas éloignés. Cependant, leur compréhension fait intervenir d’autres mathématiques, la topologie et la théorie des graphes, des branches des mathématiques d’apparition plus récente que la géométrie. Ils constituent un sujet fabuleux pour faire sentir et éprouver la puissance des mathématiques, sa délicatesse et sa rigueur.

Les entrelacs ont été utilisés dans de nombreuses civilisations comme outils et ornements, des entrelacs épiques celtiques aux enluminures perses du Coran (Figure 2).

Ils apparaissent dans la vie des pêcheurs et des vanniers, et de tout un chacun quand on lace ses chaussures ou tresse des cheveux. Ils sont d’une extrême diversité et les mathématiques peuvent aider à ordonner cette diversité, en s’interrogeant sur ce qui rapproche ou différencie ces formes. Cette étude fait partie de la topologie et notamment sa branche qu’est la théorie des nœuds.
1. LA THÉORIE DES NŒUDS
Un nœud est défini mathématiquement comme un plongement du cercle dans l’espace. Pratiquement, imaginons un bout de ficelle que l’on entortille plus ou moins sans le couper, puis dont on renoue les deux extrémités. Un entrelacs, lui, est un assemblage de plusieurs nœuds, de plusieurs bouts de ficelle fermés. L’illustration du début de cette vignette, au contraire, entrelace des rubans ouverts, qui se déploient dans une direction, c’est une tresse. La théorie des nœuds a commencé à se développer dans la deuxième moitié du 19e siècle et sa source n’est pas à proprement parler mathématique. Les physiciens William THOMSON, plus connu comme Lord KELVIN, et Peter Guthrie TAIT qui ont été parmi les premiers à y contribuer, pensaient qu’elle les aiderait à comprendre les phénomènes d’absorption et d’émission de lumière par les atomes. Et c’est ainsi que TAIT a entrepris une classification des nœuds (Figure 3).
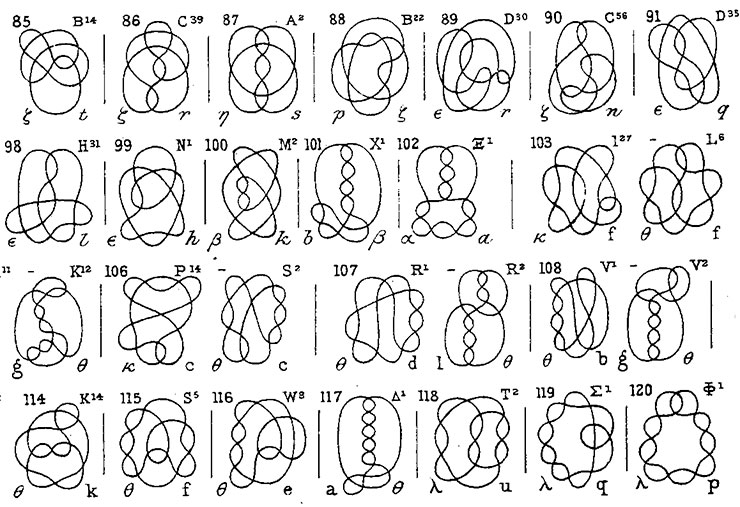
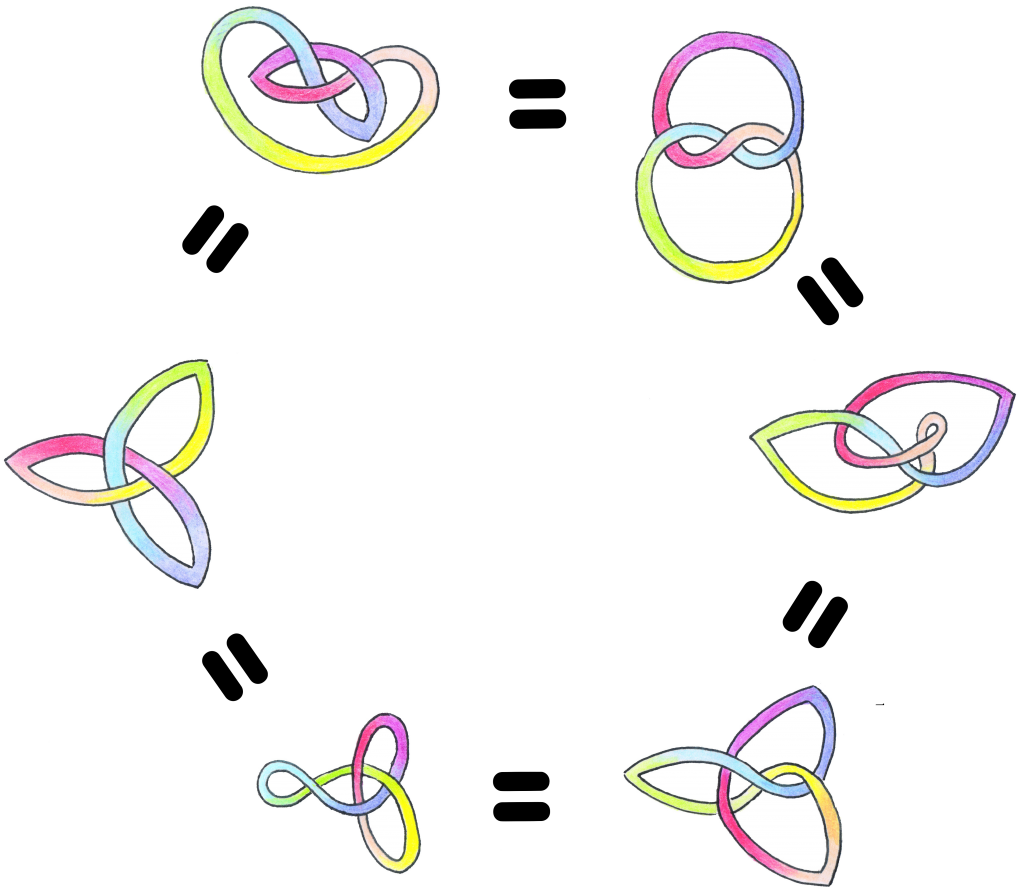
Reconnaître que deux nœuds sont dans la même classe, c’est-à-dire que l’on peut passer de l’un à l’autre par une déformation continue (que l’on appelle en mathématiques une isotopie, représentant une classe d’homologie), comme lorsque l’on essaie de démêler une ficelle nouée à ses extrémités sans la dénouer, ni la couper, n’est pas si évident, comme le montrent ces différentes images d’un même nœud de trèfle (Figure 4), qui est le nœud le plus simple qui ne soit pas trivial (c’est à dire qui ne puisse pas se réduire à un cercle).
C’est pourquoi la théorie des nœuds cherche à associer aux nœuds des quantités que ces déformations continues ne modifient pas : des invariants. Par exemple, le polynôme d’ALEXANDER est un invariant qui associe un polynôme à coefficients entiers à chaque type de nœud. Il a été découvert par James Wadell ALEXANDER en 1923 et est le premier invariant de ce type. Le polynôme d’ALEXANDER du nœud de trèfle, par exemple, est : ![]() . Nous reviendrons ensuite à cette question des invariants mais apprenons tout d’abord à tracer des entrelacs. Pour cela, nous allons les modéliser par des graphes.
. Nous reviendrons ensuite à cette question des invariants mais apprenons tout d’abord à tracer des entrelacs. Pour cela, nous allons les modéliser par des graphes.
2. ENTRELACS ET GRAPHES
Un entrelacs (ou une tresse si elle est ouverte) est un nœud à plusieurs composantes. On le représente en général par sa projection régulière dans un plan, c’est-à-dire que les brins sont dessinés se croisant transversalement et au plus deux à deux : il n’y a pas trois points du nœud qui sont projetés sur le même point du plan, les brins aux croisements ont des directions projetées différentes et les croisements sont en nombre fini. Décrire l’objet qui résulte de ces différents croisements et sa structure n’a rien d’évident.
On va pour cela en construire un modèle abstrait, en négligeant un certain nombre de paramètres comme la couleur des brins et leur épaisseur. Ce sera un graphe planaire : avec des sommets reliés par des arêtes, pas forcément rectilignes, qui ne se croisent pas et on les étiquettera d’une chiralité gauche / droite. Une projection régulière d’un entrelacs sur le plan partitionne celui-ci en zones, délimitées par la projection de l’entrelacs lui-même. Là où il y a des croisements, localement quatre zones se rencontrent. On peut, d’après le théorème de JORDAN,1 colorier toutes les zones de deux couleurs, disons noir et blanc, de telle manière que ces croisements ressemblent à un échiquier (deux zones opposées ont même couleur et deux zones contiguës ont une couleur différente).
Il suffit pour cela de décider que la zone extérieure infinie est blanche, de choisir un point dedans et de relier chaque zone par un chemin qui croise transversalement la projection de l’entrelacs et évite les croisements (Figure 5).
À chaque passage par un brin, on change de couleur. On démontre que le résultat ne dépend pas du point de départ choisi, ni du détail du trajet suivi et que l’on aboutit toujours à un coloriage cohérent. Le coloriage en effet ne dépend que de la parité du nombre de brins traversés. On associe alors un sommet à chaque zone noire et on les relie par des arêtes, tirées au-dessus de chaque croisement, d’une zone noire à son opposée. Nous attachons alors l’étiquette correspondante pour coder si c’est le brin droit ou le brin gauche qui, vu d’un sommet, passe au-dessus. Le codage est cohérent, la zone opposée donnant la même chiralité (Figure 6).
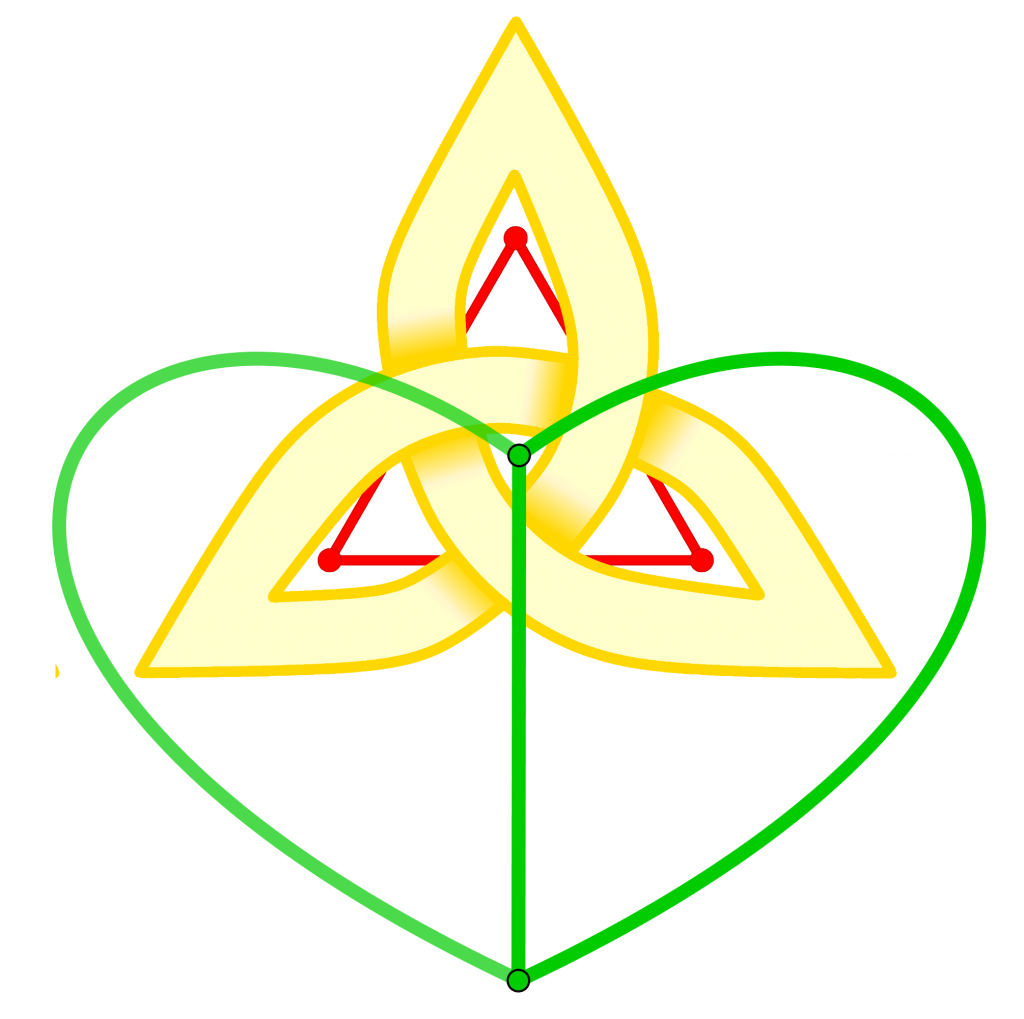
Le nœud de trèfle est ainsi associé à un triangle où toutes les arêtes ont même chiralité, disons gauche : c’est un entrelacs alterné, quand on suit un brin, il croise alternativement au-dessus, en-dessous, au-dessus. . . Mais ce n’est pas le seul graphe qui code ce nœud, il y a également le graphe à deux sommets et trois arêtes non pas droites mais courbes et étiquetées droite ! (Figure 7), qui est obtenu en positionnant les sommets dans les zones blanches.
Ces deux graphes sont ce que l’on appelle des graphes duaux. Ce codage par un graphe planaire permet de coder complètement l’entrelacs et il est beaucoup plus simple à décrire. La tresse compliquée est en fait codée par un graphe qu’on peut expliquer en une phrase, par exemple, «une échelle triangulaire à laquelle on enlève un barreau sur trois» (Figure 8).
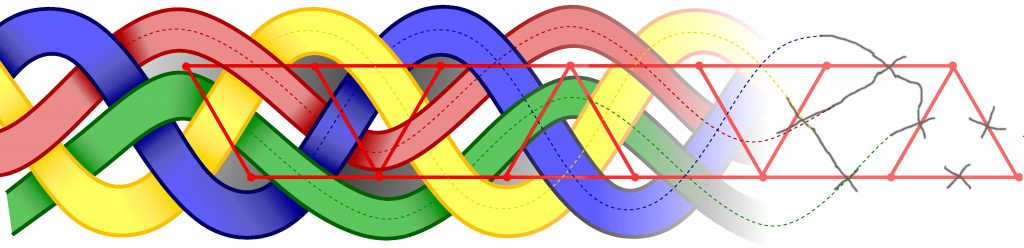
Ces graphes sont évocateurs et le mathématicien Alexandre GROTHENDIECK a nommé dessins d’enfants une grande classe de graphes (localement) planaires. Après cette phase d’analyse, procédons maintenant à la synthèse : dessiner l’entrelacs codé par un graphe. Ceci s’effectue en trois étapes présentées de la droite vers la gauche sur la Figure 8 :
- Dessiner une croix au milieu de chaque arête. Tout croisement est au milieu d’une arête.
- Relier les brins les uns aux autres en un trajet continu.
- Faire figurer les dessus-dessous.
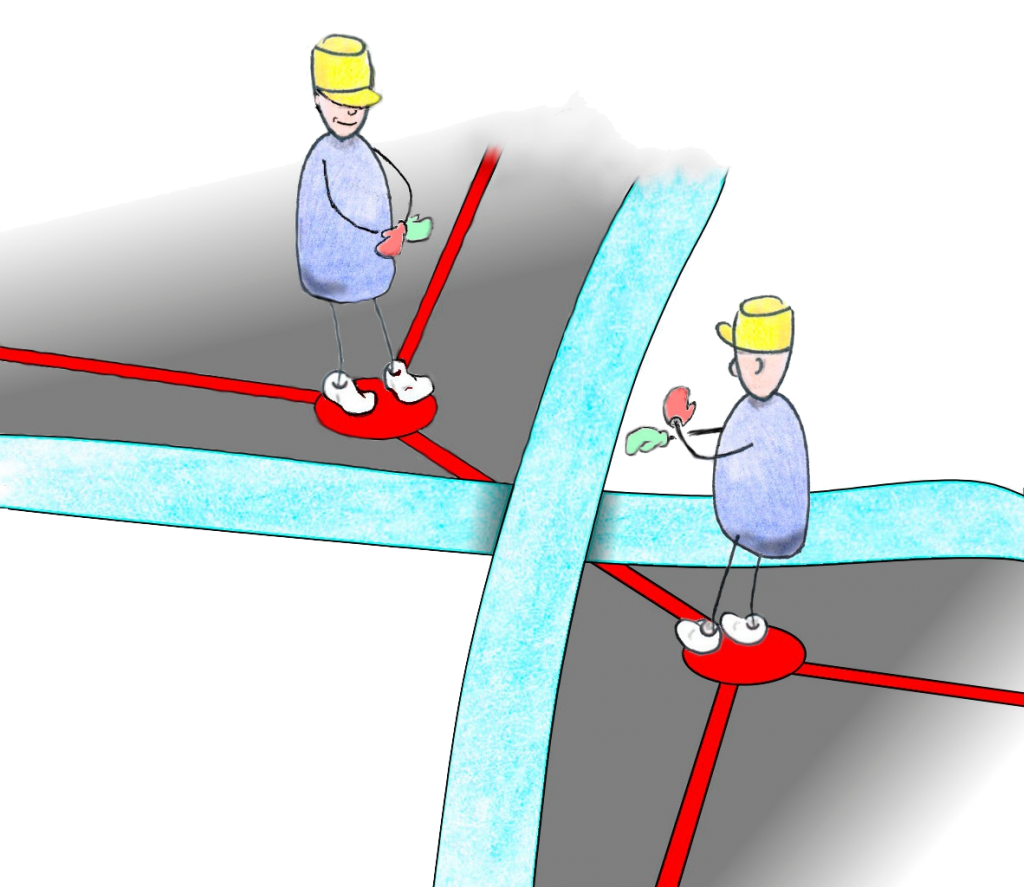
Dans le détail, une croix se dessine au crayon, inclinée entre 30 et 60° avec l’arête. Cette orientation est importante pour l’étape suivante car on continue chaque petit brin en longeant l’arête dans la direction où il pointe, on arrive ainsi au croisement suivant et on se raccorde au brin qui pointe dans cette direction. À cette étape, on n’introduit pas de nouveau croisement et les brins ne traversent les arêtes qu’aux croisements. Une métaphore est utile : imaginer les arêtes comme les murs d’un labyrinthe, qu’on suit et qu’on ne peut pas franchir, sauf aux croisements, figurant une porte (Figure 9).
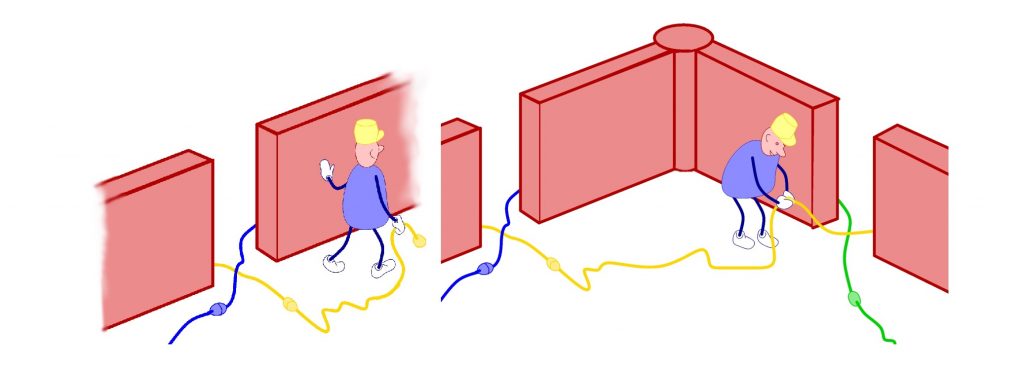
Enfin, en choisissant un croisement, en alignant l’arête qui le porte avec son regard, on identifie lequel des deux brins provient de la droite et lequel provient de la gauche, ce qui permet de remplacer le croisement par un «pont» avec un brin (disons le gauche) passant au-dessus et l’autre (le droit) en-dessous. Nous vous invitons maintenant, avant de lire la suite, à élaborer un petit graphe, de 5 ou 6 arêtes, toutes de longueurs comparables, des angles ni trop aigus ni trop obtus, et élaborer le nœud qu’il code, il suffit pour cela de jouer avec les graphes planaires. La vidéo http://video.math.cnrs.fr/entrelacs/, les exemples dans [4, 5] peuvent vous donner des idées.
3. INVARIANTS
Le premier à s’être intéressé sérieusement aux invariants est le jeune Carl Friedrich GAUSS au début du XIXe siècle, décrivant l’enlacement de deux courbes, γ1,γ2, dans l’espace, calculé comme une intégrale impressionnante mais dont la valeur est toujours un entier relatif :
![]()
Ce nombre ne se calcule pas ici à partir de la projection de l’entrelacs mais reste le même quand on déforme les courbes sans qu’elles se croisent. Cela paraît compréhensible si on est persuadé que le résultat est un entier : la formule dépend continument de chaque courbe et ne peut sauter d’une unité que quand il y a un grave problème : quand le dénominateur s’annule, c’est-à-dire quand les deux courbes se croisent. Mais on peut beaucoup plus facilement le calculer à partir de la projection, en orientant les brins et en sommant simplement des signes pour chaque croisement entre les deux courbes : +1 pour ![]() et -1 pour
et -1 pour ![]() . Quand il n’y a qu’une seule courbe, cette somme combinatoire définit un nombre, qu’on appelle l’entortillement (writhe en anglais)
. Quand il n’y a qu’une seule courbe, cette somme combinatoire définit un nombre, qu’on appelle l’entortillement (writhe en anglais) ![]() de la projection du nœud
de la projection du nœud ![]() . Le nœud de trèfle droit a ainsi un entortillement de +3. Mais que devient
. Le nœud de trèfle droit a ainsi un entortillement de +3. Mais que devient ![]() quand de menus incidents altèrent la projection ? Il y a trois types de complications qui peuvent arriver à une projection d’entrelacs, localement dans un petit disque, le reste de l’entrelacs restant le même (Figure 10):
quand de menus incidents altèrent la projection ? Il y a trois types de complications qui peuvent arriver à une projection d’entrelacs, localement dans un petit disque, le reste de l’entrelacs restant le même (Figure 10):

Dans les années vingt, BRIGGS et REIDEMEISTER ont démontré que les seules simplifications dont on avait besoin pour passer d’une projection particulière à n’importe quelle autre étaient décrites par trois mouvements. Avoir un invariant de nœud c’est donc avoir une fonction dont la valeur n’est pas modifiée par les accidents ci-dessus. Or on voit vite que, quelles que soient les orientations des brins, si les transformations II et III ne modifient pas l’entortillement, la première le modifie ! L’entortillement n’est donc pas un invariant de nœud !
Cependant, on peut réparer ces problèmes et obtenir de vrais invariants. Ce ne sont plus de simples nombres comme ![]() , mais une collection de nombres, coefficients de polynômes en une ou deux variables ou de polynômes de LAURENT avec des exposants qui peuvent être négatifs.
, mais une collection de nombres, coefficients de polynômes en une ou deux variables ou de polynômes de LAURENT avec des exposants qui peuvent être négatifs.
Les héros de cette partie de l’histoire sont James Waddell ALEXANDER en 1923, John Horton CONWAY en 1969, Vaughan JONES en 1984 et Louis KAUFFMAN en 1987. Ils ont découvert, et d’autres à leur suite, par des moyens touchant à l’algèbre ou à la physique mathématique, des manières de construire des fonctions d’entrelacs complexes comme combinaisons de la même fonction mais sur des entrelacs plus simples : ce sont les relations d’écheveau. Parmi ces fonctions, certaines sont des invariants.
Le crochet de KAUFFMAN- sa valeur
 sur le nœud trivial,
sur le nœud trivial, -
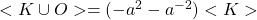 et
et -
la relation d’écheveau
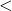

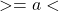
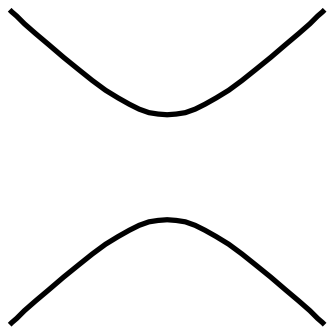
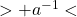
 .
.
Et à chaque fois qu’on tortille, on multiplie par ce facteur. De même, le nœud trivial d’entortillement ![]() a pour crochet
a pour crochet ![]() . Mais finalement, quand on divise le crochet par
. Mais finalement, quand on divise le crochet par ![]() , on obtient un vrai invariant!
, on obtient un vrai invariant!
Dans l’encadré ci-dessous, nous calculons le crochet de KAUFFMAN du nœud de trèfle standard, d’entortillement ![]() , les croisements supprimés successivement étant indiqués par une boule jaune.
, les croisements supprimés successivement étant indiqués par une boule jaune.
qu’on remplace ci-dessus pour donner
On aurait pu aussi appliquer trois fois les relations d’écheveau sans réfléchir pour obtenir
Les mouvements de REIDEMEISTER et les mouvements d’écheveau s’expriment également sur les graphes qui les codent (Figure 11, où les arêtes gauches sont pleines, les arêtes droites en tireté).
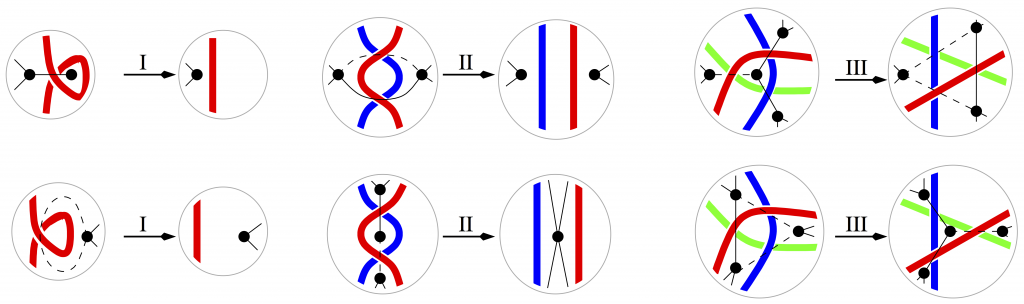
Sur le graphe, les relations d’écheveau reviennent à effacer l’arête ou confondre les sommets, ce qu’on peut noter en barrant l’arête par un tiret, en travers pour le premier cas, ou en long dans le second. À la relation d’écheveau
![]()
![]()
![]()
![]()
![]()
![]()
![]()
correspond ainsi pour le graphe la relation
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
chaque type d’arête barrée amenant un facteur ![]() ou
ou ![]() . En l’appliquant à toutes les arêtes, on se ramène à une réunion de nœuds triviaux disjoints dont le graphe se réduit à des sommets isolés affectés d’une puissance de
. En l’appliquant à toutes les arêtes, on se ramène à une réunion de nœuds triviaux disjoints dont le graphe se réduit à des sommets isolés affectés d’une puissance de ![]() comptabilisant les différents types d’arêtes barrées. L’encadré ci-après reprend le calcul du crochet de KAUFFMANN pour le graphe du nœud de trèfle:
comptabilisant les différents types d’arêtes barrées. L’encadré ci-après reprend le calcul du crochet de KAUFFMANN pour le graphe du nœud de trèfle:
![]()
![]()
![]()
![]()
![]()
![]()
![]() et en itérant, on arrive à
et en itérant, on arrive à
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
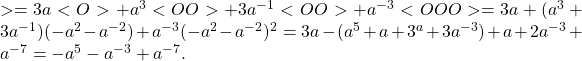
C’est en fait le crochet de KAUFFMAN du trèfle miroir du précédent, où les notions de gauche et droite sont inversées. Cette somme sur toutes les possibilités affectées d’un poids comptabilisant la contribution de chaque configuration locale s’appelle une fonction de partition en mécanique statistique.
Le polynôme de HOMFLY-PT2 d’un nœud ![]() est un peu plus élaboré, il demande qu’on oriente le nœud et a besoin de deux variables,
est un peu plus élaboré, il demande qu’on oriente le nœud et a besoin de deux variables, ![]() est ainsi défini par:
est ainsi défini par: ![]() et la relation d’écheveau
et la relation d’écheveau
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Il a la grande qualité d’être compatible avec la composition des nœuds : la somme
. Il a la grande qualité d’être compatible avec la composition des nœuds : la somme ![]() de deux nœuds s’obtient simplement en les ouvrant et en les recollant. Le polynôme de
de deux nœuds s’obtient simplement en les ouvrant et en les recollant. Le polynôme de ![]() vérifie alors
vérifie alors ![]() . Tout comme un entier peut se dé- composer en un produit de facteurs premiers (
. Tout comme un entier peut se dé- composer en un produit de facteurs premiers (![]() ), les nœuds peuvent ainsi se décomposer de manière unique en nœuds premiers. C’était l’intution chimique de KELVIN et TAIT. La figure 12 reproduit la table des nœuds premiers jusqu’à sept croisements.
), les nœuds peuvent ainsi se décomposer de manière unique en nœuds premiers. C’était l’intution chimique de KELVIN et TAIT. La figure 12 reproduit la table des nœuds premiers jusqu’à sept croisements.

4. CONCLUSION
Les entrelacs sont d’abord apparus dans l’humanité comme des outils techniques, puis des manifestations de sa créativité artistique et ce n’est que bien des siècles après qu’ils sont devenus des objets d’attention pour les scientifiques, physiciens et mathématiciens. Le développement de la topologie et de ses outils propres a permis de progresser dans la compréhension de ces objets, d’identifier des invariants. Cependant, de nombreux problèmes restent ouverts et la recherche y est très active. Très récemment, en 2020, par exemple, une conjecture concernant sur un nœud fascinant (Figure 13) découvert par John CONWAY il y a 50 ans a été démontrée par la mathématicienne Lisa PICCIRILLO.3

Certes les espoirs initiaux de THOMPSON et TAITS ont été déçus car les hypothèses sur lesquels ils se fondaient se sont révélées erronées, mais les travaux sur les tresses ont aujourd’hui des applications variées, en biologie comme on peut s’y attendre mais aussi en robotique par exemple. La topologie n’est pas un objet d’enseignement dans le secondaire et ce n’est pas non plus le cas pour ce qui est des graphes pour beaucoup d’élèves mais les diverses expériences qui ont été menées sur les entrelacs dès l’enseignement primaire, en s’appuyant sur des ressources vidéos et autres, se sont révélées très motivantes et enrichissantes pour les élèves, leur permettant de mettre de façon inattendue des mathématiques à leur portée au service de leur regard sur le monde et de la création artistique. Le site entrelacs.net en témoigne. Pour les enseignants, avoir un aperçu des mathématiques sous-jacentes est important et c’est l’objet de cette vignette.
- Le théorème de Jordan exprime que toute courbe simple et fermée du plan y délimite deux composantes connexes du plan, l’une bornée, l’autre non, dont elle est la frontière.
- Pour HOSTE, OCNEANU, MILLET, FREYD, LICKORISH, YETTER et PRZYTYCKI, TRACZYK.
- Lisa PICCIRILLO a démontré que ce nœud, qui possède la propriété d’avoir le même polynôme d’ALEXANDER-CONWAY que le nœud trivial (1), n’est pas bordant. Voir la vidéo de Mickaël LAUNAY[3] qui explique cette découverte de façon très accessible.
RÉFÉRENCES
- A. Aubin. Nœuds sauvages imaginary.org.
- L. H. Kauffman. Knots and Physics. 4th Ed, volume 53. Singapore: World Scientific, 4th ed. edition, 2013.
- M. Launay. Une énigme de 50 ans résolue : Le nœud de Conway n’est pas bordant – micmaths.
- C. Mercat. Celtic knotwork (english, french, german, spanish, italian, portuguese). http://www.entrelacs.net/.
- C.Mercat.De beaux entrelacs, video AuDiMath, Images des Mathématiques. In A. Alvarez, editor, Destination Géométrie et Topologie Avec Thurston, Voyages En Mathématiques, pages 15–26. Le Pommier, 2013.
- J.-P. Petit. Le Topologicon. Les Aventures d’Anselme Lanturlu. Belin, Savoir sans frontières edition, 1981.
- L. Piccirillo. How you too can solve 50+ year old problems – talks at google.
- D. Rolfsen. Knots and Links. 2nd Print. with Corr, volume7. Houston, TX: Publish or Perish, 2nd print. with corr. edition, 1990.
- A. Sossinsky. Knots. Origins of a mathematical theory. Paris: Éditions du Seuil, 1999.
Télécharger un pdf de cet article.
Ce post est disponible en: Anglais

 Français
Français 简体中文
简体中文  English
English  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português