Von Graeme Cohen.
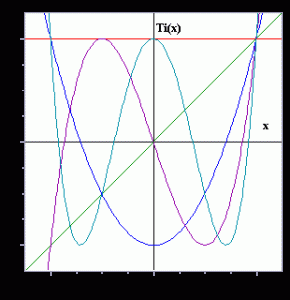
Von allen bekannten Funktionen, wie zum Beispiel den Winkel-, Exponential- oder Logarithmusfunktionen, sind sicherlich die Funktionswerte von Polynomfunktionen am leichtesten zu berechnen. Dieser Artikel soll erstens den Begriff der Potenzreihe einführen, die auch als Polynomfunktion unendlichen Grades verstanden werden kann, und zweitens zeigen, wie mit ihrer Hilfe Funktionswerte von Funktionen mit einem Taschenrechner berechnet werden können. Wenn ein Taschenrechner Werte von trigonometrischen, exponentiellen oder logarithmischen Funktionen berechnen soll, so erreicht man dieses, indem die Funktionswerte von Polynomfunktionen berechnet werden, die man für solche Potenzreihen erhält, die für jene Funktionen repräsentativ sind und ausreichend gute Näherungen darstellen. Dies ist zwar der direkte Weg, aber es gibt oft bessere Möglichkeiten. Wir werden hier insbesondere eine Potenzreihe für die Funktion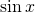 
herleiten und darlegen, wie man den direkten Ansatz verändern kann, um ihre Werte besser zu approximieren. Dabei werden wir auf Tschebyschow-Polynome zurückgreifen, die in vielerlei Hinsicht für einen ähnlichen Zweck und in vielen weiteren Anwendungen verwendet werden. (Für trigonometrische Funktionen ist der CORDIC-Algorithmus oft die bevorzugte Auswertungsmethode – ein Thema, das sich vielleicht für einen weiteren Klein-Artikel anbieten würde.)
Im Sinne von Felix Klein greifen wir hier auf einen grafischen Ansatz zurück. Ansonsten verwenden wir nur grundlegende Kenntnisse und Techniken aus Trigonometrie und Analysis.
Continue reading →
Vignette écrite par Graeme L. Cohen (University of Technology, Sydney), Steven Galbraith (University of Auckland) et Edoardo Persichetti (University of Auckland).
