Coloration de Cartes et Bases de Gröbner

Cette image est la propriété de mathscareers.org.uk, qui a aimablement autorisé son utilisation pour cet article.

Vignette écrite par Escudeiro Hernandes.
D’après le célèbre “théorème des quatre couleurs”, seulement quatre couleurs sont nécessaires pour colorier une carte sans que deux régions adjacentes aient la même couleur. En utilisant des équations polynomiales et les bases de Gröbner, nous pouvons déterminer si trois couleurs sont suffisantes pour colorier une carte donnée.

1. Coloration de carte
Le théorème des quatre couleurs (1) établit que n’importe quelle carte, qu’elle soit plane ou sphérique, peut être coloriée avec quatre couleurs sans que deux régions adjacentes soient de la même couleur. Il est facile de produire des exemples de cartes ne pouvant être coloriées avec seulement trois couleurs, et d’autre pouvant être coloriées avec trois couleurs. Une façon de déterminer si trois couleurs sont suffisantes pour colorier une carte consiste à analyser un système d’équations polynomiales associé à la carte. Chaque couleur est associée à une racine cubique (complexe) de l’unité et chaque région est symbolisée par une variable $x_i$ de sorte qu’elle ne peut qu’admettre l’une des trois valeurs, c’est-à-dire une des trois couleurs. Ainsi nous avons ${x_i}^3 - 1 = 0$ pour chaque région.

Pour des régions $x_j$ et $x_k$ , nous avons $0= x_j ^3 -x_k ^3 =(x_j -x_k)(x_j ^2 +x_j x_k + x_k ^2)$ . Si $x_j$ et $x_k$ sont des régions adjacentes, et puisque de telles régions ne peuvent pas être de la même couleur, alors $x_j \neq x_k$ , c’est-à-dire, $x_j ^2+ x_j x_k + x_k ^2=0$ . De cette façon, une carte avec $n$ régions peut être coloriée avec trois couleurs si et seulement si le système d’équations polynomiales

(1) $\begin{eqnarray*} \left\{ \begin{array}{l} x_i ^3-1=0 ~,\\ x_j ^2+ x_j x_k + x_k ^2=0 ~, \end{array}\right. \end{eqnarray*}$

où $i= 1 , ... , n$ et $x_j$ et $x_k$ représentent des régions adjacentes, admet au moins une solution.

Exemple 1.

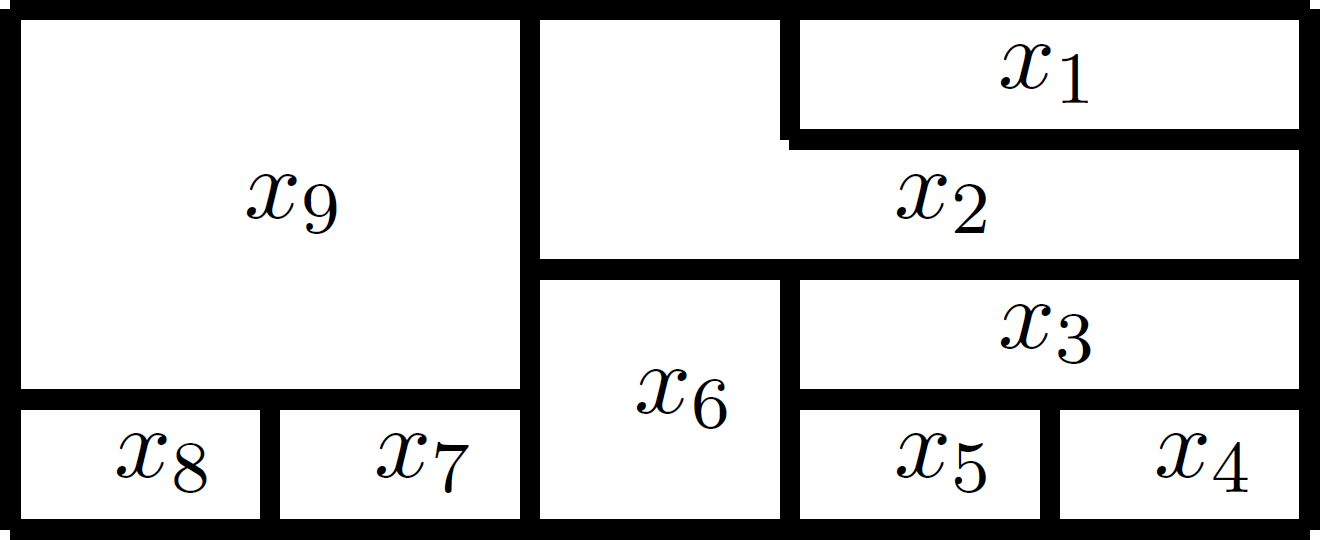
On considère la carte:

Figure 1.

Peut-elle être coloriée avec trois couleurs?

Pour répondre à cette question on doit vérifier que le système polynomial 1 avec $i = 1, ..., 9$ et

peut être résolu.

2. Systèmes d’équations polynomiales

La réponse à de nombreux problèmes de mathématiques réside dans la résolution de systèmes d’équations polynomiales, ce qui n’est pas toujours aisé. Si le système est donné par des équations linéaires, on peut, par la méthode du pivot de Gauss par exemple, substituer un système par un système équivalent dont la solution est plus facile à trouver. Dans le cas des systèmes polynomiaux, il existe une méthode analogue que nous présentons ci-dessous.

On notera $P(n)$ l’ensemble des polynômes à coefficients complexes et à variables $x_1 , ... , x_n$ . Etant donné un ensemble de polynômes $f_1, ... , f_r$ dans $P(n)$ , on définit l’idéal qu’ils engendrent par

$I = \langle f_1, ... , f_r \rangle = \{ h_1 f_1 + ... + h_r f_r \mid h_1 , ... , h_r \in P(n) \}.$

Un théorème du mathématicien David Hilbert: (2), appelé théorème des zéros de Hilbert, établit que le système $f_1 = ... = f_r = 0$ admet une solution (complexe) si et seulement si $1 \notin \langle f_1 , ... , f_r \rangle$ . Comment peut-on vérifier la dernière condition?

Il est facile de vérifier que deux systèmes d’équations $f_1 = ... = f_r = 0$ et $g_1 = ... = g_s = 0$ , où $f_i, g_j \in P (n)$ , vérifiant la condition

(2) $\begin{eqnarray*} \langle f_1 , ... , f_r \rangle = \langle g_1 , ... , g_r \rangle , \end{eqnarray*}$

ont la même solution.

Par conséquent, la stratégie pour résoudre un système $f_1 = ... = f_r = 0$ consiste à trouver des polynômes $g_1, ... , g_s$ satisfaisant la condition 2 et avec lesquels il est possible de vérifier si un élément $f \in P (n)$ appartient ou non à l’idéal $\langle f_1, ... , f_r \rangle$ et dont la solution commune est plus facile à calculer qu’avec le système d’origine.

L’existence théorique d’un tel ensemble $G = \{ g_1 , ... , g_s \}$ a été découverte durant la première moitié du siècle dernier par le mathématicien Wolfgang Gröbner. Des années plus tard, son étudiant Bruno Buchberger créa un algorithme pour le calculer. Ces ensembles sont appelés bases de Gröbner et l’algorithme de Buchberger pour les calculer est un des outils de calcul algébrique les plus importants.

Si l’idéal est de la forme $I = \langle f_1 \rangle$ , on a $f \in I$ si et seulement si $f = h_1 f_1$ , c’est-à-dire $f$ est divisible par $f_1$ . De même, $f \in \langle f_1 , ... , f_r \rangle$ si et seulement si $f = h_1 f_1 + ... + h_r f_r$ , ce qui suggère quelque chose de similaire pour la division de $f$ par $f_1 , ... , f_r$ . En fait, on peut diviser un polynôme à plusieurs variables par un ensemble fini de polynômes, à condition que les monômes soient ordonnés d’une certaine façon.

3. Les Bases de Gröbner

Un monôme $m$ de $P (n)$ est un élément de la forme $x_1 ^{a_1} ... x_n ^{a_n}$ , où $a_1 , ... , a_n$ sont des entiers positifs ou nuls. Le monôme $x_1 ^0 ... x_n ^0$ sera noté $1$ . Parmi les ordres $\preceq$ sur les monômes de $P (n)$ , ceux qui satisfont $1 \preceq m$ and $m_1 .m \preceq m_2 .m$ lorsque $m_1 \preceq m_2$ sont ceux qui rendent possible la mise en pratique de l’algorithme de division.

Un exemple est l’ordre lexicographique $\preceq_{Lex}$ , où $x_1 ^{a_1} ... x_n ^{a_n} \preceq_{Lex} x_1 ^{b_1} ... x_n ^{b_n}$ , s’il existe $1 \leqslant i \leqslant n$ de sorte que $a_i < b_i$ et $a_j = b_j$ pour tous $j < i$ .

Etant donné un ordre sur les monômes, le plus grand monôme d’un polynôme $f$ est appelé terme dominant de $f$ et noté $lt (f)$ (pour « leading term »).

Une base de Gröbner d’un idéal $I = \langle f_1 , ... , f_r\rangle$ relativement à un ordre sur les monômes, est, par définition, un ensemble $G = \{ g_1 , ... , g_s \}$ d’éléments de $I$ de sorte que le terme dominant de chaque élément de $I$ soit divisible par le terme dominant d’un élément de $G$ . On peut montrer que chaque base de Gröbner $G$ de $I$ est un ensemble qui vérifie la condition 2.

Par conséquent, $1 \in I$ si et seulement si il existe une base de Gröbner de $I$ contenant une constante non nulle, puisque $1 \preceq m$ , pour chaque monôme $m$ de $P (n)$ .

Par exemple, $G = \{ f_1 \}$ est une base de Gröbner de $\langle f_1 \rangle$ , pour tout ordre sur les monômes, alors que $G = \{ x+y+z-6, x-y+1, x+y-z \}$ n’est pas une base de Gröbner de $I = \langle x+y+z-6, x-y+1, x+y-z \rangle$ pour l’ordre lexicographique, puisque $lt(x+y+z-6-(x-y+1)) = lt(2y+z-7) = 2y$ n’est pas divisible par $x = lt(x + y + z - 6) = lt(x - y + 1) = lt(x + y - z)$ .

Pour obtenir une base de Gröbner d’un idéal, pour un ordre sur les monômes donné, on peut utiliser l’algorithme de Buchberger (3). On trouve des algorithmes permettant de calculer des bases de Gröbner dans la majorité des systèmes de calcul algébrique.

En l’occurence, une base de Gröbner de l’idéal $I = \langle x+y+z-6, x-y+1, x+y-z \rangle$ , pour l’ordre lexicographique, est $G = \{ x+y +z -6, 2y +z -7, 2z -6 \}$ .

4. Solution du problème et autres applications

Le système de l’exemple 1, a au plus un nombre fini de solutions (neuf variables, chacune pouvant prendre une valeur parmi trois). Le problème est de déterminer si le système admet une solution, et dans ce cas de la déterminer.

En appliquant l’algorithme de Buchberger au système de l’exemple 1, on obtient la base de Gröbner $G$ suivante, pour l’ordre lexicographique:

Ainsi, $1 \notin I$ et par conséquent le système admet des solutions. Les équations

$\left\{ \begin{array}{l} x_1 ^3 - 1 = 0 ~,\\ x_2 ^2 + x_2 x_1 + x_1 ^2 = 0 ~,\\ x_5 - x_2 = 0 ~,\\ x_7 - x_2 = 0 ~,\\ x_9 -x_3 = 0 ~, \end{array}\right.$

traduisent le fait suivant: on peut utiliser n’importe quelle couleur pour $x_1$ , $x_2 \neq x_1$ , $x_2 = x_5 = x_7$ et $x_3 = x_9$ .

Puisque les couleurs sont représentées par des racines cubiques complexes de l’unité, la seule solution pour $x_4 + x_3 + x_2 = 0$ , $x_6 + x_3 + x_2 = 0$ et $x_8 + x_3 + x_2 = 0$ est d’attribuer des valeurs (couleurs) distinctes pour $x_2$ , $x_3$ et $x_4$ , et donc $x_4 = x_6 = x_8$ . Enfin, $0 = x_3 ^2 + x_3 x_2 -x_2 x_1 -x_1 ^2 = (x_3 + x_2 + x_1 )(x_3 - x_1 )$ qui nous donne deux possibilités: $x_3 +x_2 +x_1 = 0$ ou $x_3 -x_1 = 0$ , c’est-à-dire $x_1$ , $x_2$ et $x_3$ ont des couleurs distinctes ou $x_1 = x_3$ . Ainsi, on trouve, à une permutation des couleurs près, toutes les solutions possibles:

Figure 2.

Les bases de Gröbner peuvent aussi être utilisées pour déterminer des idéaux, en convertisssant des équations paramétriques en équations cartésiennes (pour des surfaces et des courbes par exemples), pour calculer des polynômes minimaux de nombres algébriques, pour vérifier des théorèmes de géométrie Euclidienne, pour valider des constructions en origami et résoudre des grilles de sudoku (voir (4), (5) et (6)).

Références

(1) http://www.ipv.pt/millenium/Millenium24/12.pdf

(2) http://www.mat.uniroma1.it/people/manetti/dispense/nullstellen.pdf

(3) https://www.risc.jku.at/people/buchberg/papers/1970-00-00-A.english.pdf

(4) Adams, W. and Loustaunau, P., An Introduction to Gröbner Basis, AMS, Providence RI (1994).

(5) Cox, D; Little, J. and O’Shea, D., Ideals, Varieties and Algorithms, 2nd edition, Springer-Verlag, New York, (1996).

(6) Hernandes, M. E., Um Primeiro Contato com Bases de Gröbner, 28°. Colóquio Brasileiro de Matemática, IMPA, Rio de Janeiro, (2011).

Coloration de Cartes et Bases de Gröbner

Related

Laisser un commentaire Annuler la réponse.

Receive notice of every new vignette.

Search

Coloration de Cartes et Bases de Gröbner

Partager :

Related

Laisser un commentaire Annuler la réponse.

Receive notice of every new vignette.

Search