Colorazioni di mappe e basi di Gröbner

Questa immagine è di proprietà di mathscanners.org.uk che ha gentilmente permesso di usarla in questo lavoro.

Autore originario é Marcelo Escudeiro Hernandes.

Per il famoso “Teorema dei quattro colori”, abbiamo bisogno solo di quattro colori per colorare una mappa in modo che nessuna delle regioni confinanti abbia lo stesso colore. Usando equazioni polinomiali e basi di Gröbner possiamo determinare se tre colori sono sufficienti per una mappa specifica.

1. Colorazione di mappe
Il famoso Teorema dei Quattro Colori [1] afferma che tutte le mappe, siano esse in un piano o su una sfera, possono essere colorate con quattro colori senza che regioni confinanti siano dello stesso colore. È molto facile produrre esempi di mappe che non possono essere colorate con tre colori e di altre per le quali ciò è possibile. Un modo per decidere se tre colori sono sufficienti per colorare una particolare mappa, è quello di analizzare un sistema polinomiale associato alla mappa. Ogni colore è rappresentato da una radice cubica complessa dell’unità e ogni regione da una variabile $x_i$ che può assumere solo uno di tre valori, cioè, uno dei tre colori. Abbiamo quindi $x^3_i - 1 = 0$ per ciascuna regione.

Per regioni $x_j$ e $x_k$ abbiamo $0= x_j ^3 -x_k ^3 =(x_j -x_k)(x_j ^2 +x_j x_k + x_k ^2)$ . Se $x_j$ e $x_k$ sono regioni confinanti e, come regioni confinanti, non possono avere lo stesso colore, allora $x_j \neq x_k$ , cioè, $x_j ^2+ x_j x_k + x_k ^2=0$ . In questo modo, una mappa con n regioni può essere colorata con tre colori se e soltanto se il seguente sistema di equazioni polinomiali ammette almeno una soluzione

(1) $\begin{eqnarray*} \left\{ \begin{array}{l} x_i ^3-1=0 ~,\\ x_j ^2+ x_j x_k + x_k ^2=0 ~, \end{array}\right. \end{eqnarray*}$

dove $i = 1, ..., n$ e $x_j$ e $x_k$ rappresentano regioni adiacenti.

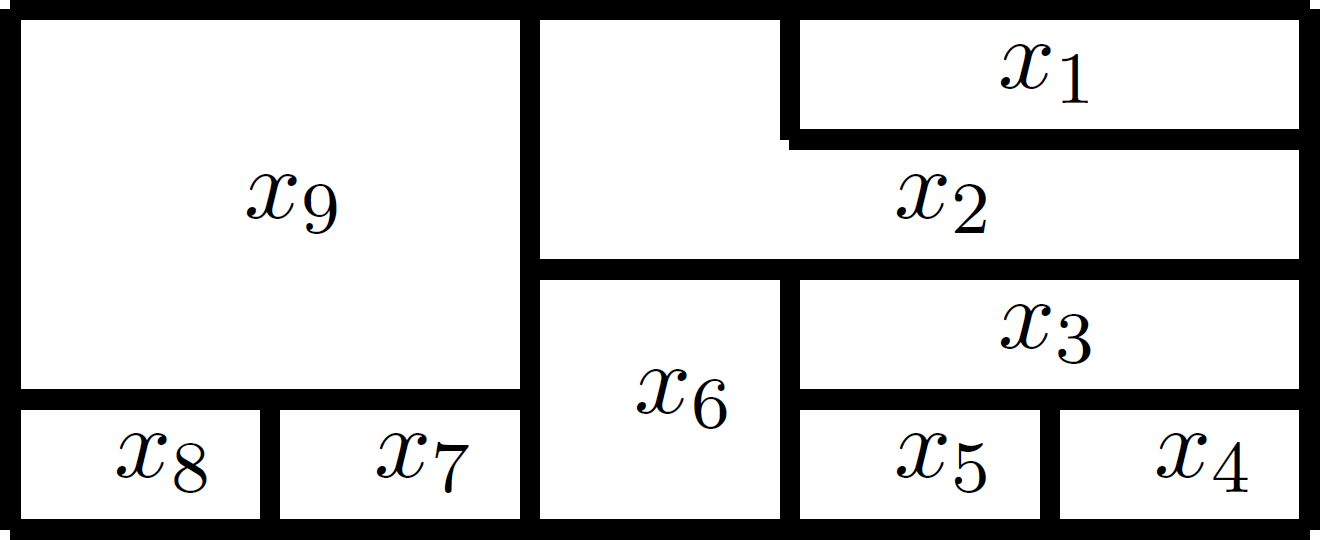
Esempio 1.

Consideriamo la mappa:

Figura 1.

Può essere colorata con tre colori?

Per rispondere a questa domanda dobbiamo verificare se si può risolvere il sistema polinomiale (1), con $i = 1, ..., 9$ e

2. Sistemi di equazioni polinomiali

La risposta a molti problemi in matematica è dovuta alla soluzione di sistemi di equazioni polinomiali, che non è sempre semplice. Se il sistema è composto da equazioni lineari, mediante eliminazione gaussiana, possiamo sostituire il sistema con un altro ad esso equivalente la cui soluzione è più semplice. Nel caso di sistemi polinomiali, si ha a disposizione un metodo analogo che descriviamo sotto.

Denoteremo con $P(n)$ l’insieme dei polinomi a coefficienti complessi con variabili $x_1 , ... , x_n$ . Dato un insieme di polinomi $f_1, ..., f_r$ in $P(n)$ , determiniamo l’ideale generato da essi:

$I = \langle f_1, ... , f_r \rangle = \{ h_1 f_1 + ... + h_r f_r \mid h_1 , ... , h_r \in P(n) \}.$

Un teorema dovuto al matematico David [2], chiamato Nullstellensatz di Hilbert, afferma che il sistema $f_1 = ... = f_r = 0$ ammette una soluzione (complessa) se e soltanto se $1 \notin \langle f_1 , ... , f_r \rangle$ . Ma come si può verificare quest’ultima condizione?

È molto semplice verificare che due sistemi di equazioni $f_1 = ... = f_r = 0$ e $g_1 = ... = g_s = 0$ , dove $f_i, g_j \in P (n)$ soddisfano alla condizione

(2) $\begin{eqnarray*} \langle f_1 , ... , f_r \rangle = \langle g_1 , ... , g_r \rangle , \end{eqnarray*}$

hanno la stessa soluzione.

Quindi, la strategia per risolvere un sistema $f_1 = ... = f_r = 0$ consiste nel trovare polinomi $g_1,...,g_s$ che soddisfano alla condizione (2) e con cui è possibile verificare se un dato $f \in P (n)$ appartiene o meno all’ideale $\langle f_1, ... , f_r \rangle$ e la cui soluzione comune è più semplice da calcolare rispetto a quella del sistema originario.

L’esistenza di tale $G = \{ g_1 , ... , g_s \}$ era stata scoperta dal punto di vista teorico nella prima metà del secolo scorso dal matematico Wolfgang Gröbner. Alcuni anni dopo, il suo studente Bruno Buchberger ha creato un algoritmo per calcolarlo. Questi insiemi sono chiamati Basi di Gröbner e l’algoritmo di Buchberger per calcolarle è uno degli strumenti più importanti del calcolo algebrico.

Se l’ideale è della forma $I = \langle f_1 \rangle$ , abbiamo $f \in I$ se e solo se $f = h_1 f_1$ , vale a dire, $f$ è divisibile per $f_1$ . Analogamente, $f \in \langle f_1 , ... , f_r \rangle$ se e solo se $f = h_1 f_1 + ... + h_r f_r$ , il che suggerisce qualcosa di simile per la divisione di $f$ per $f_1, ..., f_r$ . In effetti, possiamo dividere un polinomio in diverse variabili mediante un insieme finito di polinomi, a condizione che i monomi siano ordinati in un qualche modo.

3. Basi di Gröbner

Un monomio $m$ di $P(n)$ è un elemento della forma $x_1 ^{a_1} ... x_n ^{a_n}$ , dove $a_1 , ... , a_n$
sono interi non negativi. Il monomio $x_1 ^0 ... x_n ^0$ sarà denotato con $1$ . Tra gli ordini $\preceq$ tra i monomi di $P(n)$ , quelli che soddisfano $1 \preceq m$ e $m_1 \cdot m \preceq m_2 \cdot m$ ogni volta che $m_1 \preceq m_2$ sono quelli che permettono di applicare l’algoritmo della divisione.

Un esempio è l’ ordine lessicografico $\preceq_{Lex}$ , dove $x_1 ^{a_1} ... x_n ^{a_n} \preceq_{Lex} x_1 ^{b_1} ... x_n ^{b_n}$ , se esiste $1 \leqslant i \leqslant n$ tale che $a_i < b_i$ e $a_j = b_j$ per tutti $j < i$ .

Fissato un ordine tra i monomi, il massimo monomio di un polinomio f è chiamato il termine portante di $f$ ed è denotato con $lt(f)$ .

Una base di Gröbner di un ideale $I = \langle f_1 , ... , f_r\rangle$ rispetto ad un dato ordine tra monomi, è, per definizione, un qualunque insieme $G = \{ g_1 , ... , g_s \}$ di elementi di $I$ tale che il termine portante di un qualunque elemento di $I$ sia divisibile per il termine portante di qualche elemento di $G$ . Possiamo mostrare che una qualunque base di Gröbner $G$ di $I$ è un insieme che soddisfa la condizione (2).

Quindi, $1 \in I$ se e soltanto se esiste una base di Gröbner di $I$ che contiene una costante non nulla, poichè $1 \preceq m$ , per ogni monomio $m$ di $P (n)$ .

Per esempio, $G = \{ f_1 \}$ è una base di Gröbner di $\langle f_1 \rangle$ rispetto ad un qualsiasi ordine tra monomi, mentre $G = \{ x+y+z-6, x-y+1, x+y-z \}$ non è una base di Gröbner di $I = \langle x+y+z-6, x-y+1, x+y-z \rangle$ rispetto all’ordine lessicografico, perchè $lt(x+y+z-6-(x-y+1)) = lt(2y+z-7) = 2y$ non è divisibile per $x = lt(x + y + z - 6) = lt(x - y + 1) = lt(x + y - z)$ .

Per ottenere una base di Gröbner di un ideale, rispetto all’ordine tra monomi scelto, si può applicare l’algoritmo di BuchBerger [3]. Troviamo algoritmi per calcolare le basi di Gröbner nella maggior parte dei CAS (computer algebra systems).

Per esempio, una base di Gröbner per l’ideale $I = \langle x+y+z-6, x-y+1, x+y-z \rangle$ , rispetto all’ordine lessicografico è $G = \{ x+y +z -6, 2y +z -7, 2z -6 \}$ .

4. Soluzione del problema ed altre applicazioni

Il sistema dato nell’Esempio 1. ha al più un numero finito di soluzioni (nove variabili, di cui ognuna può assumere uno dei tre valori). Il problema è determinare se il sistema ammette una qualche soluzione, e in tal caso, trovarla.

Applicando l’algoritmo di BuchBerger al sistema dell’Esempio 1., otteniamo la seguente base di Gröbner $G$ , rispetto all’ordine lessicografico:

Quindi, $1 \notin I$ e di conseguenza il sistema ammette soluzioni. Le equazioni

$\left\{ \begin{array}{l} x_1 ^3 - 1 = 0 ~,\\ x_2 ^2 + x_2 x_1 + x_1 ^2 = 0 ~,\\ x_5 - x_2 = 0 ~,\\ x_7 - x_2 = 0 ~,\\ x_9 -x_3 = 0 ~, \end{array}\right.$

descrivono quanto segue: possiamo usare un qualunque colore per $x_1$ , $x_2 \neq x_1$ , $x_2 = x_5 = x_7$ e $x_3 = x_9$ .

Poiché i colori sono rappresentati dalle radici cubiche complesse dell’unità , l’unica soluzione per $x_4 + x_3 + x_2 = 0$ , $x_6 + x_3 + x_2 = 0$ e $x_8 + x_3 + x_2 = 0$ è attribuire valori (colori) distinti per $x_2$ , $x_3$ e $x_4$ e così $x_4 = x_6 = x_8$ . Infine,

$0 = x_3 ^2 + x_3 x_2 -x_2 x_1 -x_1 ^2 = (x_3 + x_2 + x_1 )(x_3 - x_1 )$

ci dà due possibilità : $x_3 +x_2 +x_1 = 0$ o $x_3 -x_1 = 0$ , vale a dire, $x_1$ , $x_2$ e $x_3$ assumono colori distinti oppure $x_1 = x_3$ . In tal modo, troviamo, a meno di permutazioni di colori, tutte le possibili soluzioni:

Figura 2.

Le basi di Gröbner possono anche essere usate per operare con gli ideali, convertendo equazioni parametriche in forma implicita (ad esempio, alcune superfici e curve) in equazioni non parametriche, per calcolare il polinomio minimo di numeri algebrici, per verificare teoremi di geometria euclidea, per validare costruzioni con gli Origami e per risolvere puzzle Sudoku (si veda [4], [5] e [6]).

Riferimenti bibliografici

[1] http://www.ipv.pt/millenium/Millenium24/12.pdf

[2] http://www.mat.uniroma1.it/people/manetti/dispense/nullstellen.pdf

[3] https://www.risc.jku.at/people/buchberg/papers/1970-00-00-A.english.pdf

[4] Adams, W. and Loustaunau, P., An Introduction to Gröbner Basis, AMS, Providence RI (1994).

[5] Cox, D; Little, J. and O’Shea, D., Ideals, Varieties and Algorithms, 2nd edition, Springer-Verlag, New York, (1996).

[6] Hernandes, M. E., Um Primeiro Contato com Bases de Gröbner, 28°. Colóquio Brasileiro de Matemática, IMPA, Rio de Janeiro, (2011).

Colorazioni di mappe e basi di Gröbner

Related

Laisser un commentaire Annuler la réponse

Receive notice of every new vignette.

Search

Meta

Colorazioni di mappe e basi di Gröbner

Partager :

Related

Laisser un commentaire Annuler la réponse

Receive notice of every new vignette.

Search

Meta