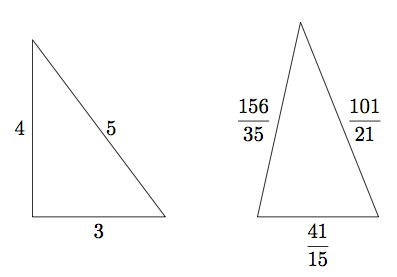 Versión original escrita por William Mc Callum.
Versión original escrita por William Mc Callum.
Si dos triángulos tienen áreas y perímetros iguales, ¿han de ser congruentes? La respuesta resulta ser que no. Por ejemplo, un triángulo de lados 3, 4 y 5 tiene el mismo área y perímetro que un triángulo con lados ![]() ,
, ![]() y
y ![]() .
.
Ambos tienen perímetro 12:
![]()
Sorprendentemente, los dos triángulos también tienen el mismo área. El primer triángulo es rectángulo y su área es ![]() . Para averiguar el área del otro triángulo usamos la fórmula de Herón, que afirma que el área
. Para averiguar el área del otro triángulo usamos la fórmula de Herón, que afirma que el área ![]() de un triángulo de lados
de un triángulo de lados ![]() ,
, ![]() y
y ![]() viene dada por
viene dada por
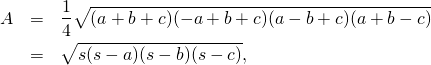
donde ![]() es el semiperímetro del triángulo. Un rápido cálculo con esta fórmula muestra que el área del segundo triángulo también es 6.
es el semiperímetro del triángulo. Un rápido cálculo con esta fórmula muestra que el área del segundo triángulo también es 6.
El espacio de triángulos
¿Cómo encontramos ejemplos como este? El secreto es encontrar la manera adecuada de representar el espacio de todos los triángulos. Hay muchas maneras posibles de hacerlo. Una es representar un triángulo con la terna ![]() de las longitudes de sus lados en algún orden. De esta manera representamos un triángulo con un punto en el espacio tridimensional. No todos los puntos corresponden con triángulos; por ejemplo, las tres coordenadas deben ser positivas. ¿Puedes pensar en otras restricciones?
de las longitudes de sus lados en algún orden. De esta manera representamos un triángulo con un punto en el espacio tridimensional. No todos los puntos corresponden con triángulos; por ejemplo, las tres coordenadas deben ser positivas. ¿Puedes pensar en otras restricciones?
Hay otra manera de poner coordenadas al espacio de triángulos usando ángulos en lugar de longitudes. Cada triángulo tiene un círculo inscrito, y el radio ![]() del círculo cumple una relación sencilla con el área
del círculo cumple una relación sencilla con el área ![]() y el semiperímetro
y el semiperímetro ![]() , en concreto
, en concreto
![]()
Para ver por qué es así, dibuja perpendiculares desde el centro del círculo a los lados del triángulo como en la parte izquierda de la Figura 2. Estas perpendiculares son las alturas de tres triángulos menores cuyas bases son los lados del triángulo grande y con vértices en el centro del círculo inscrito. Sumando las áreas de esos triángulos obtenemos ![]() .
.
-

- Figura 2: Parametrizando el espacio de triángulos
Esta ecuación nos dice que si dos triángulos tienen el mismo área y semiperímetro, el radio de sus círculos inscritos es el mismo. Así que si buscamos dos triángulos así los encontraremos entre todos los triángulos circunscritos a un círculo fijo. En lugar de usar longitudes para describir esos triángulos, usaremos los ángulos formados por los tres radios en el centro del círculo, como en la parte derecha de la Figura 2.
Parametrizando triángulos con área y perímetro constante
Dentro del espacio de triángulos podemos encontrar curvas que corresponden a familias enteras de triángulos con los mismos valores de ![]() y
y ![]() .
.
Primero, expresamos ![]() en términos de los ángulos
en términos de los ángulos ![]() ,
, ![]() y
y ![]() y el radio
y el radio ![]() del círculo inscrito, como sigue. Los radios y los segmentos que unen los vértices con el incentro dividen el triángulo en seis triángulos rectángulos. Como las líneas de los vértices al centro bisecan los ángulos del triángulo grande, esos triángulos rectángulos forman pares congruentes. Tomando una base por cada par de triángulos y sumando, tenemos
del círculo inscrito, como sigue. Los radios y los segmentos que unen los vértices con el incentro dividen el triángulo en seis triángulos rectángulos. Como las líneas de los vértices al centro bisecan los ángulos del triángulo grande, esos triángulos rectángulos forman pares congruentes. Tomando una base por cada par de triángulos y sumando, tenemos
![]()
Esta ecuación junto con ![]() nos dicen que si el área
nos dicen que si el área ![]() y el semiperímetro
y el semiperímetro ![]() son constantes, también lo son las sumas de las tangentes:
son constantes, también lo son las sumas de las tangentes:
(1) ![]()
Ahora traducimos esta condición a una ecuación que define una curva plana. Sean ![]() ,
, ![]() y
y ![]() . Como
. Como ![]() , tenemos
, tenemos
![]()
así que
![]()
Entonces, si ![]() es la constante
es la constante ![]() , la ecuación (1) se convierte, al fijar
, la ecuación (1) se convierte, al fijar ![]() , en la ecuación
, en la ecuación
(2) ![]()
(3) ![]()
Cada triángulo con área ![]() y semiperímetro
y semiperímetro ![]() determina un punto en esta curva, y cada punto en la curva dentro de una cierta región del plano corresponde a un triángulo. La región corresponde a ángulos que valgan en la Figura 2, es decir ángulos que cumplan
determina un punto en esta curva, y cada punto en la curva dentro de una cierta región del plano corresponde a un triángulo. La región corresponde a ángulos que valgan en la Figura 2, es decir ángulos que cumplan ![]() y
y ![]() , lo que corresponde a la región
, lo que corresponde a la región ![]() ,
, ![]() y
y ![]() (ya que
(ya que ![]() ).
).
La Figura 3 muestra la curva para ![]() , y el valor correspondiente al triángulo de lados 3, 4, and 5. Cada punto en la componente de esta curva que está en el cuadrante positivo corresponde a un triángulo; las longitudes de sus lados son
, y el valor correspondiente al triángulo de lados 3, 4, and 5. Cada punto en la componente de esta curva que está en el cuadrante positivo corresponde a un triángulo; las longitudes de sus lados son ![]() ,
, ![]() , y
, y ![]() . En concreto, los puntos
. En concreto, los puntos ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() y
y ![]() corresponden al triángulo de lados 3, 4 y 5 tomados en órdenes distintos.
corresponden al triángulo de lados 3, 4 y 5 tomados en órdenes distintos.
Encontrar puntos en la curva
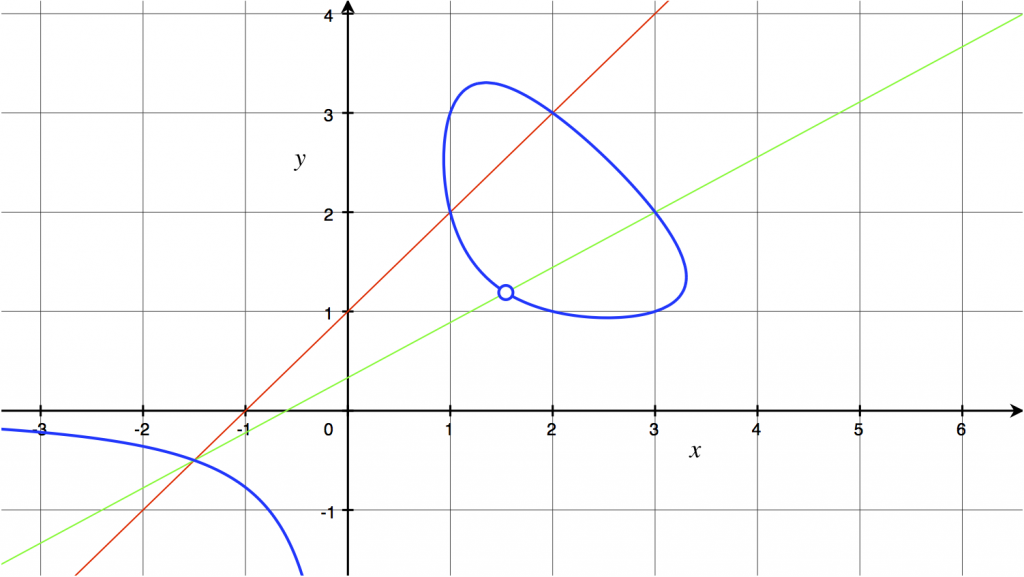
Figure 3: Curve parameterizing triangles of perimeter 12 and area 6.
Dado que la curva de la Figura 3 está definida por una ecuación de grado 3, podemos encontrar puntos en ella usando el método de las tangentes y secantes. Dos puntos en la curva determinan una recta secante que corta a la curva en un tercer punto; encontrar ese punto equivale a resolver una ecuación cúbica en ![]() , conociendo dos de sus soluciones. Como ya conocemos 6 puntos sobre la curva, tenemos muchas posibilidades para las secantes, y generando nuevos puntos tendremos todavía más. De hecho, la curva tiene infinitos puntos con coordenadas racionales. El proceso de dos secantes mostrado en la Figura 3 produce el punto
, conociendo dos de sus soluciones. Como ya conocemos 6 puntos sobre la curva, tenemos muchas posibilidades para las secantes, y generando nuevos puntos tendremos todavía más. De hecho, la curva tiene infinitos puntos con coordenadas racionales. El proceso de dos secantes mostrado en la Figura 3 produce el punto ![]() (marcado con un círculo), que corresponde al triángulo de lados
(marcado con un círculo), que corresponde al triángulo de lados ![]() ,
, ![]() y
y ![]() .
.
El método de las secantes funciona en cualquier curva cúbica en el plano; tales curvas se llaman curvas elípticas (no porque las curvas sean elipses, sino porque surgen del estudio de ciertas clases de funciones complejas llamadas funciones elípticas). El método de las secantes nos permite definir una estructura de grupo en el conjunto de puntos con coordenadas racionales de una curva elíptica.
El estudio de las curvas elípticas es un área central de investigación en teoría de números, con aplicaciones a los sistemas criptográficos que hay detrás de las transacciones financieras por internet. Las curvas elípticas jugaron un papel fundamental en la demostración del último teorema de Fermat.
La historia descrita en este artículo muestra la extraordinaria unidad de las matemáticas, empezando por las matemáticas de bachillerato y llegando hasta las de investigación. Por el camino hemos encontrado una idea fundamental en la matemática moderna: la de resolver un problema sobre un tipo particular de objeto (triángulos con área 6 y perímetro 12, por ejemplo) situando el objeto en un espacio más general (el espacio de todos los triángulos) y encontrando la manera correcta de parametrizar ese espacio.

Felicitaciones por tan esmerado, didáctico y esclarecedor artículo; gracias por la gran labor que hacen.
Encontré un detalle que, supongo, debería ser más explícito.
Dada la ecuación (2) x + y + z = s*s/A, dónde: s = (a + b + c)/2.
Y las condiciones:
a = x + y, b = x + z, c = y + z
Despejando:
z = (b + c – a) / 2,
Y reemplazando:
a = x + y
Se obtiene:
A = (a + b + c)/2
Por lo tanto, el espacio de triángulos obtenido está restringido a aquellos cuya área es igual al semiperímetro. Aunque se anuncia (primer párrafo, tercera sección), no se especifica en términos matemáticos: A = s.
Esto da lugar a confusión, pues en el apartado inmediatamente anterior A = rs.