 Die Autoren des englischen Artikels sind Michèle Artigue und Ferdinando Arzarello.
Die Autoren des englischen Artikels sind Michèle Artigue und Ferdinando Arzarello.
Die Analyse der Entwicklung eines Naturphänomens führt oft zur Untersuchung numerischer Folgen, insbesondere deren Langzeit-Verhalten und zu der Frage, ob sie eventuell konvergieren. Polynomiale, exponentielle und logarithmische Folgen werden häufig in weiterführenden Schulen behandelt, andere Folgen mit sehr einfachen Bildungsgesetzen zeigen dagegen ein viel komplexeres Verhalten. Beispiele sind die chaotischen Folgen, die bei der Untersuchung dynamischer Systeme auftreten (siehe [1]) und die Syrakus-Folge (oder ![]() -Folge), die 1937 von Lother Collatz eingeführt wurde. Die Syrakus-Folge forderte Mathematiker über Jahrzehnte heraus. Trotz der riesigen Anzahl von Werten, die berechnet wurden, ist es zurzeit unbekannt, ob die Folge divergiert oder letztlich immer bei
-Folge), die 1937 von Lother Collatz eingeführt wurde. Die Syrakus-Folge forderte Mathematiker über Jahrzehnte heraus. Trotz der riesigen Anzahl von Werten, die berechnet wurden, ist es zurzeit unbekannt, ob die Folge divergiert oder letztlich immer bei ![]() endet (siehe [2]).
endet (siehe [2]).
Die Folgen, die in diesem Klein-Artikel betrachtet werden, wurden 1944 von dem britischen Logiker R.L. Goodstein eingeführt (siehe [3]) und zeigen verschiedene Arten eines ungewöhnlichen Verhaltens. Ihre Anfangswerte steigen so schnell, dass man glauben könnte, dass sie gegen Unendlich streben, aber, erstaunlicherweise, fallen die Folgenglieder irgendwann und erreichen letztendlich die Null. Der Beweis dieses Ergebnisses erfordert eine Verallgemeinerung des Wohlordnungs- Prinzips der ganzen Zahlen (siehe [4]) zu den transfiniten Zahlen. Dabei ist die Grundidee nicht schwer zu verstehen. Um dies – wie Hodgson – zu erklären (siehe [5]), führen wir zunächst eine verwandte Folge ein, die wir schwache Goodstein-Folge nennen, die einfacher, aber eng mit der Goodstein-Folge verwandt ist.
1. Schwache Goodstein-Folgen
Bei Hodgson wird die Definition einer schwachen Goodstein-Folge beginnend mit der Zahl ![]() dargestellt. Wie alle positiven natürlichen Zahlen besitzt sie eine eindeutige Zerlegung in eine Summe von Potenzen mit der Basis
dargestellt. Wie alle positiven natürlichen Zahlen besitzt sie eine eindeutige Zerlegung in eine Summe von Potenzen mit der Basis ![]() (siehe [6]):
(siehe [6]): ![]() . Die schwache Goodstein-Folge mit dem Anfangsglied
. Die schwache Goodstein-Folge mit dem Anfangsglied ![]() ist wie folgt definiert: um den Wert von
ist wie folgt definiert: um den Wert von ![]() zu erhalten, verändert man die Basis
zu erhalten, verändert man die Basis ![]() von
von ![]() zur Basis
zur Basis ![]() , subtrahiert
, subtrahiert ![]() und schreibt die sich daraus resultierenden Zahlen zur Basis
und schreibt die sich daraus resultierenden Zahlen zur Basis ![]() um. Folglich erhält man:
um. Folglich erhält man: ![]() . Zur Bestimmung von
. Zur Bestimmung von ![]() ändert man die Basisdarstellung von
ändert man die Basisdarstellung von ![]() zur Basis
zur Basis ![]() , subtrahiert
, subtrahiert ![]() und schreibt die daraus resultierenden Zahlen zur Basis
und schreibt die daraus resultierenden Zahlen zur Basis ![]() um. Folglich erhält man:
um. Folglich erhält man: ![]() . Dies wird so lange fortgesetzt, solange alle Glieder ungleich Null sind, indem man die natürliche Zahl in der Basis des vorherigen Glieds durch die nächst größere natürliche Zahl ersetzt,
. Dies wird so lange fortgesetzt, solange alle Glieder ungleich Null sind, indem man die natürliche Zahl in der Basis des vorherigen Glieds durch die nächst größere natürliche Zahl ersetzt, ![]() subtrahiert, und das Ergebnis unter Verwendung der neuen Basis umschreibt.
subtrahiert, und das Ergebnis unter Verwendung der neuen Basis umschreibt.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Tabelle 1: Anfangsglieder einer schwachen Goodstein-Folge
Da die Glieder der Folge schnell sehr groß werden, wird man sich fragen, ob alle derartigen Folgen so schnell wachsen. Das ist aber nicht der Fall. Wenn z.B. ![]() , ist, dann folgt
, ist, dann folgt ![]() . Wenn
. Wenn ![]() ist, dann gilt
ist, dann gilt ![]() ,
, ![]() und
und ![]() (da die Basis von
(da die Basis von ![]() gleich
gleich ![]() und die Basis für
und die Basis für ![]() gleich
gleich ![]() ist). Ähnlich kann man überprüfen, dass für
ist). Ähnlich kann man überprüfen, dass für ![]() die Glieder der Folge nie größer als
die Glieder der Folge nie größer als ![]() werden und in
werden und in ![]() Schritten die Null erreichen (siehe [7]). Sobald die Zerlegung für den Anfangswert eine höhere Potenz als
Schritten die Null erreichen (siehe [7]). Sobald die Zerlegung für den Anfangswert eine höhere Potenz als ![]() beinhaltet, führt das schnelle Ansteigen der Glieder (wie für
beinhaltet, führt das schnelle Ansteigen der Glieder (wie für ![]() gezeigt) zu der Vermutung, dass die Folgen divergieren. Wie kann das Subtrahieren von
gezeigt) zu der Vermutung, dass die Folgen divergieren. Wie kann das Subtrahieren von ![]() in jedem Schritt dem enormen Anstieg der Folge durch das kontinuierliche Erhöhen der Basis um
in jedem Schritt dem enormen Anstieg der Folge durch das kontinuierliche Erhöhen der Basis um ![]() entgegenwirken?
entgegenwirken?
Wirft man einen genaueren Blick auf die Glieder der obigen Tabelle, stellt man fest, dass – obwohl die Glieder der Folge mit dem Anfangswert 266 schnell ansteigen – die Exponenten der aufeinanderfolgenden Basen zu fallen scheinen. Der Exponent ![]() in
in ![]() z.B. ist in
z.B. ist in ![]() nicht mehr vorhanden, ähnlich ist Exponent
nicht mehr vorhanden, ähnlich ist Exponent ![]() in
in ![]() ersetzt durch eine
ersetzt durch eine ![]() in
in ![]() . Und bei
. Und bei ![]() ist er zu
ist er zu ![]() reduziert. Schließlich wird der Exponent
reduziert. Schließlich wird der Exponent ![]() bei
bei ![]() zu einer
zu einer ![]() reduziert, und diese
reduziert, und diese ![]() wird in weiteren Schritten weiter reduziert. Genau diese, für alle Goodstein-Folgen auftretende Charakteristik ermöglicht es zu zeigen, dass sie gegen Null konvergieren. Für den Beweis benötigen wir die transfiniten Ordinalzahlen.
wird in weiteren Schritten weiter reduziert. Genau diese, für alle Goodstein-Folgen auftretende Charakteristik ermöglicht es zu zeigen, dass sie gegen Null konvergieren. Für den Beweis benötigen wir die transfiniten Ordinalzahlen.
2. Transfinite Ordinalzahlen und Wohlordnungen
Ordinalzahlen:
In der Alltagssprache werden Ordinalzahlen dazu verwendet, um Positionen in einer Reihenfolge anzugeben: erster, zweiter, dritter, usw. Tatsächlich können die positiven natürlichen Zahlen dazu verwendet werden, um Elemente jeder endlichen Menge in dieser Art und Weise zu ordnen. Die Idee der transfiniten Ordinalzahlen erweitert den Begriff Ordinalzahl. Diese ist auf den Mathematiker Georg Cantor zurückzuführen, der sie in einer Reihe von Artikeln Ende des 19. Jahrhunderts entwickelte. Wenn wir uns vorstellen mit der Null zu beginnen und sukzessive mit natürlichen Zahlen weiter zu zählen, würden wir nie damit fertig werden, da die Menge der natürlichen Zahlen unendlich ist. Wir können uns jedoch vorstellen, dass es eine „Zahl“ ![]() gibt, welche die erste Zahl größer als jede natürliche Zahl ist. Da unendlich viele natürliche Zahlen kleiner sind als
gibt, welche die erste Zahl größer als jede natürliche Zahl ist. Da unendlich viele natürliche Zahlen kleiner sind als ![]() , nennen wir dies eine „transfinite“ Ordinalzahl. Diese hat einen Nachfolger
, nennen wir dies eine „transfinite“ Ordinalzahl. Diese hat einen Nachfolger ![]() , auf den
, auf den ![]() folgt usw. Die kleinste Ordinalzahl größer als alle Ordinalzahlen der Form
folgt usw. Die kleinste Ordinalzahl größer als alle Ordinalzahlen der Form ![]() wird mit
wird mit![]() oder
oder ![]() bezeichnet (siehe [8]). Die kleinste Ordinalzahl, die größer ist als alle Ordinalzahlen der Form
bezeichnet (siehe [8]). Die kleinste Ordinalzahl, die größer ist als alle Ordinalzahlen der Form ![]() (wobei
(wobei ![]() eine Ordinalzahl kleiner als
eine Ordinalzahl kleiner als ![]() ist) wird mit
ist) wird mit ![]() bezeichnet. Die kleinste Ordinalzahl, die größer ist als alle Ordinalzahlen der Form
bezeichnet. Die kleinste Ordinalzahl, die größer ist als alle Ordinalzahlen der Form ![]() (wobei
(wobei ![]() eine Ordinalzahl kleiner als
eine Ordinalzahl kleiner als ![]() ist) wird mit
ist) wird mit ![]() bezeichnet.
bezeichnet.
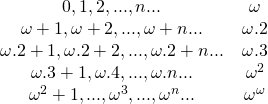
Dann wird ![]() gefolgt von
gefolgt von ![]() ,
, ![]() , … ,
, … , ![]() ,
, ![]() , …,
, …, ![]() , … ,
, … , ![]() , …,
, …, ![]() , usw. Wir definieren
, usw. Wir definieren ![]() als die kleinste Ordinalzahl, die größer als alle Summen von iterierten Potenzen von
als die kleinste Ordinalzahl, die größer als alle Summen von iterierten Potenzen von ![]() ist, und erlauben, dass es immer so weitergeht. In der Tat bilden alle bis hier genannten Ordinalzahlen nur den Beginn einer Kette von Ordinalzahlen, da sie eine abzählbare Menge bilden. D.h. sie können eins zu eins mit den positiven natürlichen Zahlen in Beziehung gesetzt werden.
ist, und erlauben, dass es immer so weitergeht. In der Tat bilden alle bis hier genannten Ordinalzahlen nur den Beginn einer Kette von Ordinalzahlen, da sie eine abzählbare Menge bilden. D.h. sie können eins zu eins mit den positiven natürlichen Zahlen in Beziehung gesetzt werden.
Ordinalzahlen und Wohlordnungen:
Ein wesentlicher Unterschied zwischen transfiniten Ordinalzahlen und nicht-negativen natürlichen Zahlen ist, dass jede natürliche Zahl größer als ![]() einen unmittelbaren Vorgänger hat, während Ordinalzahlen wie
einen unmittelbaren Vorgänger hat, während Ordinalzahlen wie ![]() ,
, ![]() und
und ![]() dies nicht haben. Allerdings, so wie die Menge der natürlichen Zahlen, ist auch die erweiterte Menge der Ordinalzahlen in dem Sinne „wohlgeordnet“, dass jede nichtleere Menge von Ordinalzahlen ein kleinstes Element hat. Diese Eigenschaft ist der Grund dafür, dass es keine unendliche streng fallende Folge von Ordinalzahlen gibt. Angenommen, so eine unendliche Folge
dies nicht haben. Allerdings, so wie die Menge der natürlichen Zahlen, ist auch die erweiterte Menge der Ordinalzahlen in dem Sinne „wohlgeordnet“, dass jede nichtleere Menge von Ordinalzahlen ein kleinstes Element hat. Diese Eigenschaft ist der Grund dafür, dass es keine unendliche streng fallende Folge von Ordinalzahlen gibt. Angenommen, so eine unendliche Folge ![]() ,
, ![]() ,
, ![]() , …, existiere. Sei
, …, existiere. Sei ![]() die Menge aller Glieder und nicht leer. Dann hat die Menge mindestens ein Element
die Menge aller Glieder und nicht leer. Dann hat die Menge mindestens ein Element ![]() , also gilt
, also gilt ![]() für eine natürliche Zahl
für eine natürliche Zahl ![]() . Aber solange die Folge streng fällt, gilt
. Aber solange die Folge streng fällt, gilt ![]() . Somit ist
. Somit ist ![]() nicht das kleinste Element von
nicht das kleinste Element von ![]() , was ein Widerspruch zur Annahme ist. Wir werden nun zeigen, wie man die Ordinalzahlen verwenden kann, um das Ergebnis über die schwachen Goodstein-Folgen zu zeigen.
, was ein Widerspruch zur Annahme ist. Wir werden nun zeigen, wie man die Ordinalzahlen verwenden kann, um das Ergebnis über die schwachen Goodstein-Folgen zu zeigen.
3. Der Beweis, dass eine schwache Goodstein-Folge gegen Null konvergiert
Jeder schwachen Goodstein-Folge ![]() wird eine streng fallende Folge von Ordinalzahlen
wird eine streng fallende Folge von Ordinalzahlen ![]() zugeordnet, indem man die Basis jeden Glieds
zugeordnet, indem man die Basis jeden Glieds ![]() durch
durch ![]() ersetzt. Da die Anfangsbasis einer schwachen Goodstein-Folge 2 ist und die Basis bei jedem Schritt um 1 ansteigt, führt dies bei
ersetzt. Da die Anfangsbasis einer schwachen Goodstein-Folge 2 ist und die Basis bei jedem Schritt um 1 ansteigt, führt dies bei ![]() zur Basis
zur Basis ![]() . Somit hat die Folge, die der mit dem Anfangswert
. Somit hat die Folge, die der mit dem Anfangswert ![]() entspricht, folgende Anfangswerte:
entspricht, folgende Anfangswerte:
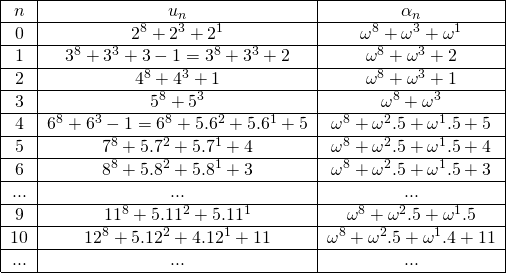
Tabelle 2: Die Folge von Ordinalzahlen, die einer schwachen
Goodstein-Folge zugeordnet ist
Jeder Term ![]() ist größer als der dazugehörige Term
ist größer als der dazugehörige Term ![]() . Während
. Während ![]() jedoch ansteigt, fällt
jedoch ansteigt, fällt ![]() . Der Grund dafür ist, dass in der Entwicklung von
. Der Grund dafür ist, dass in der Entwicklung von ![]() mit der Basis
mit der Basis ![]() der Term von
der Term von ![]() entweder Null oder ungleich Null ist. Es gibt zwei verschiedene Wege, um von dem einem zum anderen Glied zu gelangen:
entweder Null oder ungleich Null ist. Es gibt zwei verschiedene Wege, um von dem einem zum anderen Glied zu gelangen:
- Wenn
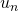 ungleich Null ist, dann ist
ungleich Null ist, dann ist 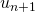 um eins kleiner als
um eins kleiner als 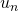 , da man bei jedem Schritt
, da man bei jedem Schritt  subtrahiert. (In Tabelle 2 kann man dies anhand den Schritte von
subtrahiert. (In Tabelle 2 kann man dies anhand den Schritte von 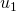 zu
zu 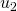 , von
, von 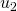 zu
zu 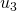 , von
, von 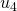 zu
zu 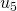 , und von
, und von 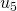 zu
zu 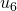 beobachten.)
beobachten.) - Wenn
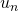 gleich Null ist, muss man den Term mit dem kleinsten Exponent zerlegen. (In Tabelle 2 kann man dies anhand der Schritten von
gleich Null ist, muss man den Term mit dem kleinsten Exponent zerlegen. (In Tabelle 2 kann man dies anhand der Schritten von 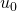 zu
zu 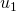 , von
, von 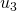 zu
zu 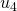 , und von
, und von 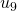 zu
zu 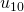 beobachten. Siehe Tabelle 1 für die Details der Berechnungen.) (siehe [9])
beobachten. Siehe Tabelle 1 für die Details der Berechnungen.) (siehe [9])
Beachten Sie, dass in beiden Fällen ![]() echt kleiner ist als der vorhergehende. Da die Ordinalzahlen geordnet sind, gibt es keine unendliche streng fallende Folge von Ordinalzahlen und somit muss eine natürliche Zahl
echt kleiner ist als der vorhergehende. Da die Ordinalzahlen geordnet sind, gibt es keine unendliche streng fallende Folge von Ordinalzahlen und somit muss eine natürliche Zahl ![]() existieren für die gilt
existieren für die gilt ![]() . Weiterhin, da
. Weiterhin, da ![]() für alle
für alle ![]() , also muss
, also muss ![]() gleich Null sein.
gleich Null sein. ![]() erreicht nach einer endlichen Anzahl an Schritten die Null, auch wenn die Anzahl der Schritte sehr groß sein kann.
erreicht nach einer endlichen Anzahl an Schritten die Null, auch wenn die Anzahl der Schritte sehr groß sein kann.
Man kann nun fragen, für welchen Wert von ![]() die Gleichung
die Gleichung ![]() gilt, wenn man die Glieder von
gilt, wenn man die Glieder von ![]() und
und ![]() angefangen mit
angefangen mit ![]() betrachtet. Was ist der Wert von
betrachtet. Was ist der Wert von ![]() und was sind die nachfolgenden Glieder für jede der zwei Folgen? (siehe [10]).
und was sind die nachfolgenden Glieder für jede der zwei Folgen? (siehe [10]).
Untersucht man nun die Goodstein-Folgen genauer, stellt man fest, dass sie ein wenig anders definiert sind als die schwachen Goodstein-Folgen, und sie wachsen noch viel spektakulärer. Dennoch ist die Beweisstrategie dafür, dass sie letztendlich gegen Null konvergieren – erstaunlicherweise – ähnlich zu der eben betrachteten Strategie.
4. Goodstein-Folgen
Betrachtet man die Darstellung von ![]() zur Basis
zur Basis ![]() .
. ![]() und schreibt man die Exponenten nur unter der Verwendung der Basis
und schreibt man die Exponenten nur unter der Verwendung der Basis ![]() , so erhält man:
, so erhält man: ![]() und
und ![]() . Infolgedessen kann der ganze Ausdruck von
. Infolgedessen kann der ganze Ausdruck von ![]() mit Basen kleiner gleich
mit Basen kleiner gleich ![]() geschrieben werden. Sei
geschrieben werden. Sei ![]() die Goodstein-Folge, die mit
die Goodstein-Folge, die mit ![]() startet. Um
startet. Um ![]() zu erhalten, ersetzt man den Wert
zu erhalten, ersetzt man den Wert ![]() in allen vorkommenden Basen und Exponenten durch den Wert
in allen vorkommenden Basen und Exponenten durch den Wert ![]() , subtrahiert 1 und schreibt das Ergebnis, ohne die Verwendung größerer Zahlen als die mit der Basis
, subtrahiert 1 und schreibt das Ergebnis, ohne die Verwendung größerer Zahlen als die mit der Basis ![]() . Um sukzessive Terme von
. Um sukzessive Terme von ![]() zu erhalten, setzt man wie in Tabelle 3 gezeigt diesen Prozess iterativ fort. (siehe [11]).
zu erhalten, setzt man wie in Tabelle 3 gezeigt diesen Prozess iterativ fort. (siehe [11]).
![]()
![]()
![]()
![]()
![]()
![]()
Tabelle 3
Aus Tabelle 3 wird das spektakuläre Wachstum der Terme ersichtlich und dennoch fängt diese Folge, wie alle Goodstein-Folgen, letztendlich an zu fallen und konvergiert schließlich gegen Null. Der Beweis ist dem Beweis für eine schwache Goodstein-Folge sehr ähnlich. Man setzt eine Folge ![]() mit der Folge
mit der Folge ![]() in Beziehung, indem man jede vorkommende Basis durch
in Beziehung, indem man jede vorkommende Basis durch ![]() ersetzt. So erhält man folgende Terme für
ersetzt. So erhält man folgende Terme für ![]() :
:
![]()
![]()
![]()
![]()
![]()
![]()
Das strenge Fallen der Folge ![]() von Ordinalzahlen impliziert, dass sie ein letztes Element hat. Die Terme können so lange berechnet werden, bis das letzte Element der Folge Null ist. Eine ähnliche Argumentation kann für alle Goodstein-Folgen verwendet werden. Gewöhnliche Arithmetik mit natürlichen Zahlen wird oft als Peano-Arithmetik bezeichnet, da der italienische Mathematiker Giuseppe Peano im 19. Jahrhundert als Erster ihre Axiome formulierte. Das Bemerkenswerteste über den obigen eleganten Beweis ist, dass er über die Peano-Arithmetik hinausgeht, um ein Theorem zu beweisen, dass komplett in der Peano-Arithmetik liegt. Mit anderen Worten: Es wird eine verallgemeinerte Mengentheorie, die transfinite Ordinalzahlen beinhaltet, verwendet, um ein Theorem über nicht-negative natürliche Zahlen, nämlich dass jede Goodstein-Folge gegen die Null konvergiert, zu beweisen. Es ist naheliegend sich zu fragen, ob die Konvergenz der Goodstein-Folge ohne Rückgriff auf transfinite Ordinalzahlen bewiesen werden kann. Die Antwort ist nein! Dies wurde 1982 von Laurie Kirby und Jeff Paris bewiesen, ca. 40 Jahre nachdem die Folgen eingeführt wurden (siehe [12]). Sie zeigten, falls die Konvergenz nur durch die Verwendung des Ordnungsprinzips der natürlichen Zahlen bewiesen werden kann (d.h. innerhalb der Peano-Arithmetik), dann kann der Satz über Goodstein-Folgen auf einen Satz von Gentzen (1936) zurückgeführt werden, aus dem die Widerspruchsfreiheit der Peano-Arithmetik abgeleitet werden kann. Wir wissen aber aus dem Unvollständigkeitstheorem von Gödel (1931), dass die Widerspruchsfreiheit der Peano-Arithmetik nicht nur mit der Peano-Arithmetik bewiesen werden kann. Es ist daher nicht anzuraten, nach einem Beweis zu suchen!
von Ordinalzahlen impliziert, dass sie ein letztes Element hat. Die Terme können so lange berechnet werden, bis das letzte Element der Folge Null ist. Eine ähnliche Argumentation kann für alle Goodstein-Folgen verwendet werden. Gewöhnliche Arithmetik mit natürlichen Zahlen wird oft als Peano-Arithmetik bezeichnet, da der italienische Mathematiker Giuseppe Peano im 19. Jahrhundert als Erster ihre Axiome formulierte. Das Bemerkenswerteste über den obigen eleganten Beweis ist, dass er über die Peano-Arithmetik hinausgeht, um ein Theorem zu beweisen, dass komplett in der Peano-Arithmetik liegt. Mit anderen Worten: Es wird eine verallgemeinerte Mengentheorie, die transfinite Ordinalzahlen beinhaltet, verwendet, um ein Theorem über nicht-negative natürliche Zahlen, nämlich dass jede Goodstein-Folge gegen die Null konvergiert, zu beweisen. Es ist naheliegend sich zu fragen, ob die Konvergenz der Goodstein-Folge ohne Rückgriff auf transfinite Ordinalzahlen bewiesen werden kann. Die Antwort ist nein! Dies wurde 1982 von Laurie Kirby und Jeff Paris bewiesen, ca. 40 Jahre nachdem die Folgen eingeführt wurden (siehe [12]). Sie zeigten, falls die Konvergenz nur durch die Verwendung des Ordnungsprinzips der natürlichen Zahlen bewiesen werden kann (d.h. innerhalb der Peano-Arithmetik), dann kann der Satz über Goodstein-Folgen auf einen Satz von Gentzen (1936) zurückgeführt werden, aus dem die Widerspruchsfreiheit der Peano-Arithmetik abgeleitet werden kann. Wir wissen aber aus dem Unvollständigkeitstheorem von Gödel (1931), dass die Widerspruchsfreiheit der Peano-Arithmetik nicht nur mit der Peano-Arithmetik bewiesen werden kann. Es ist daher nicht anzuraten, nach einem Beweis zu suchen!
Auf der anderen Seite ist es überraschend, dass die Konvergenz der schwachen Goodstein-Folgen gegen Null innerhalb der Peano-Arithmetik bewiesen werden kann. Der Grund dafür ist im Wesentlichen, dass die Terme der verknüpften Folgen von Ordinalzahlen kleiner gleich ![]() sind. Ein Beweis wurde 1987 von E.A. Cichon gegeben, der die schwachen Goodstein-Folgen einführte (siehe [13]). Zu jedem Glied
sind. Ein Beweis wurde 1987 von E.A. Cichon gegeben, der die schwachen Goodstein-Folgen einführte (siehe [13]). Zu jedem Glied ![]() einer schwachen Goodstein-Folge kann man das
einer schwachen Goodstein-Folge kann man das ![]() -Tupel von Koeffizienten der Entwicklung mit der Zerlegung in eine Basis
-Tupel von Koeffizienten der Entwicklung mit der Zerlegung in eine Basis ![]() zuordnen und zeigen, dass die
zuordnen und zeigen, dass die ![]() -Tupel eine streng fallende lexikographische Wohlordnung darstellen.
-Tupel eine streng fallende lexikographische Wohlordnung darstellen.
5. Goodstein-Folgen und das Hydra Spiel
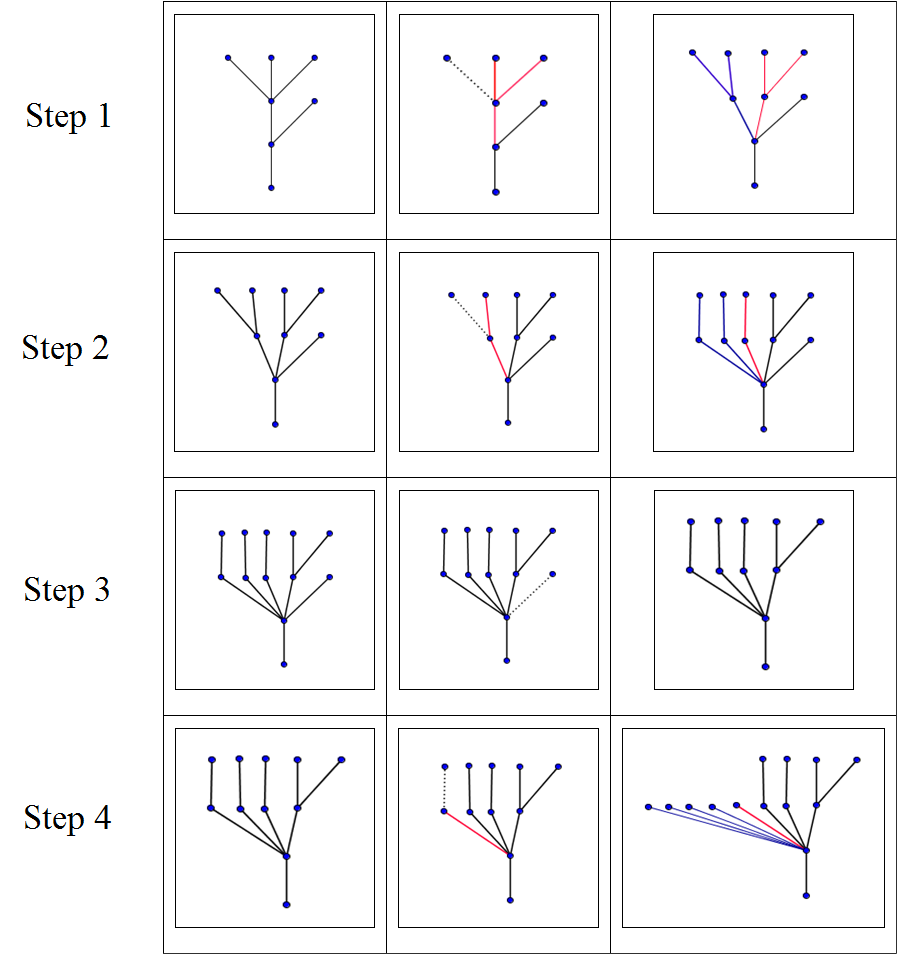
In ihrem Artikel erwähnen Kirby und Paris einen anderen Prozess, das Hydra-Spiel, der viele Ähnlichkeiten zu den Goodstein-Folgen besitzt. Das Spiel (siehe [14]) bekam seinen Namen von der Beschreibung der griechischen Mythologie des Kampfes zwischen Herakles und einer vielköpfigen Bestie: die lernäischen Hydra. Jedes Mal, wenn einer der Hydraköpfe abgeschlagen wurde, wuchsen an derselben Stelle zwei neue Köpfe nach. In diesem Spiel wird die Hydra durch einen Baum modelliert und die Köpfe der Hydra entsprechen den Endknoten oder Blättern des Baumes. Wenn Herakles einen Kopf, der nicht direkt mit der Wurzel des Baumes verbunden war, abschlägt, wird die Kante , die zum Kopf führt, entfernt. Der Hydra wachsen jedoch neue Köpfe aus den Verzweigungsknoten, die unter dem abgetrennten Kopf liegen. Dies kann auf verschiedenen Wegen realisiert werden. In dem Beispiel, das von Kirby und Paris gegeben und von Hodgson wieder verwendet wurde (siehe [4]): Wenn ein Kopf im Schritt ![]() des Spieles abgetrennt wurde, generiert die Hydra
des Spieles abgetrennt wurde, generiert die Hydra ![]() Kopien aus dem Teil des Baumes oberhalb des Verzweigungsknotens von dem der Kopf entfernt wurde. In dem unten aufgeführten Diagramm wird der Teil, der abgetrennt wird, als gepunktete Linie dargestellt, der regenerierte Teil in Rot und der Teil, der neu wachsen wird, ist in Blau dargestellt.
Kopien aus dem Teil des Baumes oberhalb des Verzweigungsknotens von dem der Kopf entfernt wurde. In dem unten aufgeführten Diagramm wird der Teil, der abgetrennt wird, als gepunktete Linie dargestellt, der regenerierte Teil in Rot und der Teil, der neu wachsen wird, ist in Blau dargestellt.
Man kann zeigen, dass bei beliebiger Anfangskonfiguration der Köpfe der Hydra und beliebiger Strategie des Herakles, er immer im Abschlagen aller Köpfe erfolgreich sein wird, obwohl er eine außergewöhnlich lange Zeit brauchen kann, um dies zu beenden. Wie bei den Goodstein-Folgen beruht der Beweis auf einer Beziehung zwischen aufeinander folgenden Bäumen und einer streng fallenden Folge von Ordinalzahlen. Wie man schon an dem obigen Diagramm erkennen kann, werden die Bäume immer breiter, aber die Höhe sich verringert schließlich. Letzlich ist Herakle sin einer Position alle Köpfe, die mehr als eine Ebene über der Wurzel liegen, zu entfernen. An diesem Punkt (wie Schritt 3 zeigt) kann er einen nach dem anderen von den übrig gebliebenen Köpfen abschlagen, ohne dass neue nachwachsen.
6. Die Lehren aus diesem Beispiel
Die Beispiele in dieser Kurzdarstellung sind aus mehreren Gründen interessant. Sie zeigen, dass mathematische Logik für mehr als nur Metamathematik relevant ist, dass Theoreme wie das Gödelsche Unvollständigkeitstheorem und Begriffe wie transfinite Ordinalzahlen für die Untersuchung gewöhnlicher mathematischer Objekte sowie für die Folgen von natürlichen Zahlen und mathematischer Graphen (hier Bäume) gebraucht werden. Durch den Beweis, dass eine Eigenschaft der natürlichen Zahlen innerhalb der allgemeinen Mengentheorie, aber nicht innerhalb der Peano-Arithmetik bewiesen werden kann, lenken diese Beispiele unsere Aufmerksamkeit auf den sprachlichen und theoretischen Rahmen der Beweise. In diesem Fall zeigen sie, dass die Peano -Arithmetik schwächer als die gewöhnliche Mengentheorie ist.
Eine andere Lehre aus diesen Beispielen ist die Strategie, ein schwieriges Problem zu lösen(hier die die Konvergenz der allgemeinen Goodstein-Folgen), indem man es in ein einfacher zugänglicheres Problem umwandelt (die Konvergenz einer schwachen Goodstein-Folge). Zusätzlich zeigen die Beispiele, dass ein typisches Beispiel – eine Folge, deren Anfangswert ![]() ist – alle wichtigen Eigenschaften des allgemeinen Falls verdeutlichen kann. Die Beispiele sind auch lehrreich, da sie uns die Grenzen unserer Intuition aufzeigen. Folgen die anscheinend divergieren, tun dies aber nicht; sie beginnen letztlich zu fallen und konvergieren in einer endlichen Anzahl an Schritten gegen die Null. Schließlich ermöglichen uns die Beispiele beides zu sehen, die Stärken und die Grenzen von Computern, da sie uns ein Gefühl für das schnelle Anwachsen der Glieder der Folge vermitteln, aber sie sind von begrenztem Nutzen, wenn man mit der Flut der numerischen Daten, die durch die Definition der Folge generiert werden, konfrontiert wird.
ist – alle wichtigen Eigenschaften des allgemeinen Falls verdeutlichen kann. Die Beispiele sind auch lehrreich, da sie uns die Grenzen unserer Intuition aufzeigen. Folgen die anscheinend divergieren, tun dies aber nicht; sie beginnen letztlich zu fallen und konvergieren in einer endlichen Anzahl an Schritten gegen die Null. Schließlich ermöglichen uns die Beispiele beides zu sehen, die Stärken und die Grenzen von Computern, da sie uns ein Gefühl für das schnelle Anwachsen der Glieder der Folge vermitteln, aber sie sind von begrenztem Nutzen, wenn man mit der Flut der numerischen Daten, die durch die Definition der Folge generiert werden, konfrontiert wird.
Literatur
[1] Elert, Glenn (1995-2007). The Chaos HypertextbookTM, Bodnar, M. & Ramsden P. Discrete Logistic Equation, Wolfram Demonstrations Project. Perrin, D. (2008). La suite logistique et le chaos.
[2] Lagarias, J. C. (2001) The Syracuse Problem. In Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer.
[3] Goodstein, R. L. (1944). On the Restricted Ordinal Theorem, Journal of Symbolic Logic, 9, 33-41.
[4] Das Wohlordnungs-Prinzip der ganzen Zahlen sagt aus: Wenn jedes Element in einer Menge ![]() ganzer Zahlen größer ist als eine bestimmte Zahl
ganzer Zahlen größer ist als eine bestimmte Zahl ![]() , dann hat
, dann hat ![]() ein kleines Element.
ein kleines Element.
[5] Hodgson B. (2004). Herculean of Sisyphean tasks? EMS Newsletter, March 2004, pp. 11-16.
[6] Gegeben sei eine ganze Zahl ![]() mit
mit ![]() , jede positive ganze Zahl
, jede positive ganze Zahl ![]() hat eine Darstellung der folgenden Form zur Basis
hat eine Darstellung der folgenden Form zur Basis ![]() :
: ![]() , wobei alle
, wobei alle ![]() wobei alle
wobei alle ![]() und
und ![]() und
und ![]() sind. Beachte, dass
sind. Beachte, dass ![]() . Dies ist eine Verallgemeinerung der Darstellung von Zahlen im Stellenwertsystem zur Basis
. Dies ist eine Verallgemeinerung der Darstellung von Zahlen im Stellenwertsystem zur Basis ![]() .
.
[7] Wenn ![]() , dann ist
, dann ist ![]() ,
, ![]() ,
, ![]() ,
, ![]() , und
, und ![]() . Beginnend mit
. Beginnend mit ![]() , ist jeder folgende Term um
, ist jeder folgende Term um ![]() geringer als der vorhergehende, weil in jedem Fall die Basis größer ist als im vorhergehenden Term.
geringer als der vorhergehende, weil in jedem Fall die Basis größer ist als im vorhergehenden Term.
[8] Wir Erweiterten die Summen- und Produktoperationen von den ganzen Zahlen zu den transfiniten Ordinalzahlen, allerdings bleibt die Kommutativität von Addition und Multiplikation nicht erhalten.
[9] Im Allgemeinen, wenn ![]() Null ist, dann hat der kleinste Term von
Null ist, dann hat der kleinste Term von ![]() die Form
die Form ![]() , wobei
, wobei ![]() eine positive ganze Zahl ist und es gilt:
eine positive ganze Zahl ist und es gilt: ![]() . Da die Basis um
. Da die Basis um ![]() größer wird und weil
größer wird und weil ![]() vom Ergebnis abgezogen wird, ist die Entwicklung von
vom Ergebnis abgezogen wird, ist die Entwicklung von ![]() :
: ![]() .
.
Der Koeffizient der kleinsten Hochzahl der Basis ist um ![]() reduziert und der Term
reduziert und der Term ![]() wird um eins kleiner als die neue Basis.
wird um eins kleiner als die neue Basis.
[10] Die Antwort lautet wie folgt: ![]() mit
mit ![]() , also
, also ![]() . Um
. Um ![]() , zu erhalten, ersetzt man die Basis
, zu erhalten, ersetzt man die Basis ![]() durch die Basis
durch die Basis ![]() und subtrahiert
und subtrahiert ![]() . Also gilt:
. Also gilt: ![]() , also
, also ![]() . Da die Basis von
. Da die Basis von ![]()
![]() ist und da
ist und da ![]() , haben – beginnend mit dem Index
, haben – beginnend mit dem Index ![]() – die Folgen
– die Folgen ![]() und
und ![]() die gleichen Werte. Sie bilden eine abnehmende arithmetische Folge mit der konstanten Differenz
die gleichen Werte. Sie bilden eine abnehmende arithmetische Folge mit der konstanten Differenz ![]() , woraus dann folgt, dass
, woraus dann folgt, dass ![]() .
.
[11] Der Term von ![]() – in Tab. 3 – wurde berechnet mit: http://www.wolframalpha.com.
– in Tab. 3 – wurde berechnet mit: http://www.wolframalpha.com.
[12] Kirby, L. and Paris, J. (1982). Accessible Independence Results for Peano Arithmetic, Bulletin of the London Mathematical Society, 14, 285-293.
[13] Cichon, E. A. (1983). A Short Proof of Two Recently Discovered Independence Results Using Recursion Theoretic Methods, Proc. Amer. Math. Soc., 87, 704-706.
[14] Bauer, A. Java applet for the Hydra Game. (Falls das Applet in einem Browser nicht läuft, versuchen Sie es mit einem anderen Browser) Dehornoy, P. (2001) L’infini est-il nécessaire? Pour la Science, Dossier, and Dehornoy, P. (2009) Cantor et les infinis.
Anmerkung: Der Artikel wurde von Herbert Glaser, Christin Landeck und Hans-Georg Weigand (Universität Würzburg – www.dmuw.de) vom Englischen ins Deutsche übersetzt.
Weitere Klein-Artikel in in anderen Sprachen verfügbar: Englisch, Französisch, …

Pingback: Von der Rekursion zur Induktion | Klein Project Blog