 A autora original é Michèle Artigue, Ferdinando Arzarello and Susanna Epp.
A autora original é Michèle Artigue, Ferdinando Arzarello and Susanna Epp.
O estudo da evolução de um fenômeno natural leva, com frequência, ao estudo de sequências numéricas, especialmente ao estudo dos seus comportamentos assintóticos (ou de longo prazo) e de suas convergências. No ensino médio encontramos com frequência sequências aritméticas, polinomiais, exponenciais e logarítmicas, mas algumas outras sequências de definição bem simples podem exibir um comportamento mais complexo. Exemplo disso são as sequências caóticas que surgem nos estudo de sistemas dinâmicos (ver [1]) e a sequência Siracusa (ou “![]() “) , introduzida por Luther Collatz, em 1937. A sequência Siracusa tem desafiado os matemáticos por décadas, e apesar de se já ter calculado uma quantidade imensa de seus valores, até o momento não se sabe se a sequência é infinita ou finita e se sempre termina em 1 (ver [2])
“) , introduzida por Luther Collatz, em 1937. A sequência Siracusa tem desafiado os matemáticos por décadas, e apesar de se já ter calculado uma quantidade imensa de seus valores, até o momento não se sabe se a sequência é infinita ou finita e se sempre termina em 1 (ver [2])
As sequências consideradas neste artigo foram introduzidas pelo lógico britânico R.L. Goodstein, em 1944 (ver [3]), e exibem um tipo diferente de comportamento estranho. Os seus valores iniciais crescem tão rapidamente que somos levados a acreditar que elas tendem a infinito, mas, para a nossa surpresa, eles sempre terminam decrescendo até finalmente alcançarem ![]() . A prova deste fato requer uma generalização do princípio da boa ordem dos números inteiros (ver [4]) para os números transfinitos, mas a ideia básica não é difícil de entender. Para explicá-la, como Hodgson [5], primeiramente introduzimos um tipo de sequência, chamada Goodstein Fraca, que é mais simples, mas relacionada à sequência de Goodstein.
. A prova deste fato requer uma generalização do princípio da boa ordem dos números inteiros (ver [4]) para os números transfinitos, mas a ideia básica não é difícil de entender. Para explicá-la, como Hodgson [5], primeiramente introduzimos um tipo de sequência, chamada Goodstein Fraca, que é mais simples, mas relacionada à sequência de Goodstein.
1. Sequências de Goodstein fracas
Seguindo Hodgson, ilustramos a definição de sequências de Goodstein fraca começando com o número 266. Como qualquer número inteiro positivo, ele possui uma única decomposição como soma de potências de ![]() (ver[2]):
(ver[2]): ![]() . A sequência de Goodstein fraca com termo inicial
. A sequência de Goodstein fraca com termo inicial ![]() é definida do seguinte modo: para obter
é definida do seguinte modo: para obter ![]() , substituímos a base
, substituímos a base ![]() na expansão acima pela base
na expansão acima pela base ![]() e, em seguida, subtraímos 1. Reescrevemos o resultado na base
e, em seguida, subtraímos 1. Reescrevemos o resultado na base ![]() :
: ![]() . Para obter
. Para obter ![]() , começamos substituindo a base
, começamos substituindo a base ![]() pela base
pela base ![]() na decomposição de
na decomposição de ![]() e subtraímos 1 do resultado. Assim
e subtraímos 1 do resultado. Assim ![]() . Enquanto não obtivermos
. Enquanto não obtivermos ![]() podemos proceder do mesmo modo: substituindo a base
podemos proceder do mesmo modo: substituindo a base ![]() da expansão pelo seu sucessor
da expansão pelo seu sucessor ![]() , subtraindo 1 e escrevendo o resultado na nova base,
, subtraindo 1 e escrevendo o resultado na nova base, ![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Tabela 1: Termos iniciais de uma sequência fraca de Goodstein
Como você pode ver, os termos da sequência rapidamente tornam-se muito grandes, portanto, é natural perguntar se todas as sequências construídas dessa maneira crescem da mesma forma. Mas, de fato, isso não acontece. Por exemplo, se ![]() , então
, então ![]() . Se tomarmos
. Se tomarmos ![]() , então,
, então, ![]() ,
, ![]() e
e ![]() (pois a base para
(pois a base para ![]() é 4 e a base para
é 4 e a base para ![]() é 5). Você pode verificar que se
é 5). Você pode verificar que se ![]() , então os termos da sequência nunca são maiores do que 3 e atingem o valor
, então os termos da sequência nunca são maiores do que 3 e atingem o valor ![]() em cinco passos (ver [7]). Entretanto, desde que a decomposição para os valores iniciais
em cinco passos (ver [7]). Entretanto, desde que a decomposição para os valores iniciais ![]() incluam potências de 2 maiores do que
incluam potências de 2 maiores do que ![]() , o crescimento inicial da sequência é muito rápido (como no caso
, o crescimento inicial da sequência é muito rápido (como no caso ![]() ). Isso leva-nos a crer que a sequência cresce arbitrariamente ( isto é, tende a infinito). Como o fato de subtrair meramente 1 em cada passo pode contrabalançar o enorme crescimento dos termos que são obtidos pela substituição do inteiro da base pelo seu sucessor?
). Isso leva-nos a crer que a sequência cresce arbitrariamente ( isto é, tende a infinito). Como o fato de subtrair meramente 1 em cada passo pode contrabalançar o enorme crescimento dos termos que são obtidos pela substituição do inteiro da base pelo seu sucessor?
Ainda assim, vamos olhar com mais cuidado para as espressões na tabela 1 acima. Apesar de os primeiros termos da sequência de valor inicial 266 crescerem rapidamente, os expoentes das representações em bases sucessivas tendem a diminuir. Por exemplo, o expoente 1 de 2 no termo ![]() já não existe na expansão de
já não existe na expansão de ![]() . Analogamente, o expoente 3 em
. Analogamente, o expoente 3 em ![]() é substituído por 2 em
é substituído por 2 em ![]() e ao chegarmos a
e ao chegarmos a ![]() torna-se igual a
torna-se igual a ![]() . O expoente
. O expoente ![]() em
em ![]() irá reduzir-se a 7 e continuará a reduzir-se mais adiante.
irá reduzir-se a 7 e continuará a reduzir-se mais adiante.
Esta é a característica comum a todas as sequências de Goodstein que permitirá provar que todas convergem a ![]() . Para ver isso, precisamos lançar mão, como prometido, dos números ordinais.
. Para ver isso, precisamos lançar mão, como prometido, dos números ordinais.
2. Números ordinais transfinitos e boa ordenação
Em linguagem comum, números ordinais são usados para indicar posição em uma lista: primeiro, segundo, terceiro, etc. De fato, os números inteiros positivos podem ser usados para posicionar dessa maneira os elementos de um conjunto finito qualquer.A ideia de número ordinal transfinito estende a noção de número ordinal. Ela foi desenvolvida por Georg Cantor em uma série de artigos publicados no final do Século XIX. Como o conjunto dos números inteiros é infinito, se imaginarmos começando com ![]() e contando sucessivamente os inteiros, nunca terminaremos. Porém, podemos imaginar que existe um “número”
e contando sucessivamente os inteiros, nunca terminaremos. Porém, podemos imaginar que existe um “número” ![]() que é o primeiro número maior do que qualquer número inteiro positivo.
que é o primeiro número maior do que qualquer número inteiro positivo. ![]() é chamado um número ordinal “transfinito”, porque existem infinitos números inteiros positivos menores do que
é chamado um número ordinal “transfinito”, porque existem infinitos números inteiros positivos menores do que ![]() . O sucessor de
. O sucessor de ![]() , denotamos por
, denotamos por ![]() , que é seguido de
, que é seguido de ![]() e assim por diante. O menor ordinal que é maior do que qualquer ordinal da forma
e assim por diante. O menor ordinal que é maior do que qualquer ordinal da forma ![]() é denotado por
é denotado por ![]() ou
ou ![]() (ver [8]) e o menor ordinal que é maior do que qualquer ordinal da forma
(ver [8]) e o menor ordinal que é maior do que qualquer ordinal da forma ![]() (com
(com ![]() um ordinal menor do que
um ordinal menor do que ![]() ) é denotado por
) é denotado por ![]() . O menor ordinal maior do que qualquer ordinal da forma
. O menor ordinal maior do que qualquer ordinal da forma ![]() (com
(com ![]() um ordinal menor do que
um ordinal menor do que ![]() ) é denotado por
) é denotado por ![]() .
.
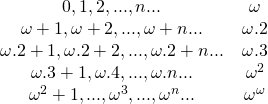
Continuando, ![]() é seguido por
é seguido por ![]() ,
, ![]() , …,
, …,![]() ,…,
,…,![]() , …,
, …, ![]() ,… e definimos
,… e definimos ![]() como o menor número ordinal maior do que todas as somas de potências iteradas de
como o menor número ordinal maior do que todas as somas de potências iteradas de ![]() e continuamos com o processo indefinidamente. De fato, todos os ordinais considerados até aqui constituem apenas o início de uma cadeia de ordinais, pois formam um conjunto enumerável, isto é, podem ser colocados em correspondência 1 a 1 com os números inteiros positivos.
e continuamos com o processo indefinidamente. De fato, todos os ordinais considerados até aqui constituem apenas o início de uma cadeia de ordinais, pois formam um conjunto enumerável, isto é, podem ser colocados em correspondência 1 a 1 com os números inteiros positivos.
Ordinais e boa ordenação:
Uma diferença significativa entre ordinais transfinitos e inteiros não negativos é que cada inteiro maior do que ![]() possui um antecessor imediato, enquanto ordinais do tipo
possui um antecessor imediato, enquanto ordinais do tipo ![]() ,
, ![]() e
e ![]() , não. Entretanto, assim como os números inteiros, o conjunto de números ordinais estendido é “bem ordenado” no sentido de que todo subconjunto não vazio de ordinais possui um menor elemento. Esta propriedade implica na não existência de uma sequência infinita estritamente decrescente de números ordinais. Suponha o contrário, e seja
, não. Entretanto, assim como os números inteiros, o conjunto de números ordinais estendido é “bem ordenado” no sentido de que todo subconjunto não vazio de ordinais possui um menor elemento. Esta propriedade implica na não existência de uma sequência infinita estritamente decrescente de números ordinais. Suponha o contrário, e seja ![]() uma tal sequência. Denote por
uma tal sequência. Denote por ![]() o conjunto dos seus elementos. Como
o conjunto dos seus elementos. Como ![]() é não vazio, existe o menor elemento, digamos
é não vazio, existe o menor elemento, digamos ![]() , para algum índice
, para algum índice ![]() . Mas como a sequência é estritamente decrescente,
. Mas como a sequência é estritamente decrescente, ![]() , ou seja,
, ou seja, ![]() não é o menor elemento de
não é o menor elemento de ![]() . Obtivemos assim uma contradição.
. Obtivemos assim uma contradição.
Mostraremos agora como usar os números ordinais para provar o resultado sobre sequências de Goodstein fracas.
3. Provando que uma sequência de Goodstein fraca converge a zero
A cada sequência de Goodstein fraca ![]() associamos uma sequência estritamente
associamos uma sequência estritamente
decrescente de ordinais ![]() substituindo a base da expansão de
substituindo a base da expansão de ![]() pelo ordinal
pelo ordinal ![]() . Observe que a decomposição de
. Observe que a decomposição de ![]() possui base
possui base ![]() , pois, como vimos, a base inicial de
, pois, como vimos, a base inicial de ![]() é 2, a de
é 2, a de ![]() é 3 e em cada passo, a base é acrescida de 1. Por exemplo, na sequência associada a 266, os termos iniciais da sequência
é 3 e em cada passo, a base é acrescida de 1. Por exemplo, na sequência associada a 266, os termos iniciais da sequência ![]() são exibidos na Tabela 2;
são exibidos na Tabela 2;
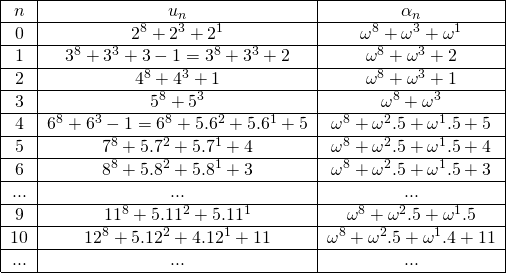
Tabela 2: A sequência de ordinais correpondentes a uma sequência Goodstein fraca
Por construção, cada termo ![]() é maior do que o termo correspondente
é maior do que o termo correspondente ![]() , mas enquanto
, mas enquanto ![]() é uma sequência crescente, a sequência
é uma sequência crescente, a sequência ![]() é decrescente. A razão disso é que na decomposição de
é decrescente. A razão disso é que na decomposição de ![]() na base
na base ![]() , o termo unitário ( ou o resto da divisão de
, o termo unitário ( ou o resto da divisão de ![]() pela base) pode ser nulo ou não e a passagem de um termo para o termo seguinte pode ocorrer de duas maneiras:
pela base) pode ser nulo ou não e a passagem de um termo para o termo seguinte pode ocorrer de duas maneiras:
- Se o termo unitário é não nulo, então como em cada passo subtraímos 1, o termo unitário diminui de 1. (Na Tabela 2, isso ocorre na passagem de
 para
para  , de
, de 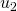 para
para 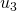 , de
, de 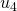 para
para 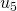 e de
e de 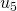 para
para 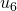 ).
). - Se o termo unitário de
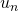 é nulo, quando escrevemos
é nulo, quando escrevemos 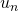 na nova base, o termo do menor expoente é particionado em duas parcelas.(Na Tabela 2, isso ocorre quando vamos de
na nova base, o termo do menor expoente é particionado em duas parcelas.(Na Tabela 2, isso ocorre quando vamos de 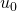 para
para 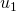 , de
, de 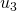 para
para 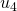 e de
e de 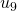 para
para  . Veja a Tabela 1 para o caminho detalhado.
. Veja a Tabela 1 para o caminho detalhado.
Observe que em ambos os casos, o novo termo ![]() correspondente é estritamente menor do que o termo que o precede.
correspondente é estritamente menor do que o termo que o precede.
Como os ordinais são bem ordenados, não existe uma sequência estritamente decrescente infinita de ordinais, portanto, deve existir o menor elemento do conjunto ![]() . Isto é, existe um índice
. Isto é, existe um índice ![]() tal que
tal que ![]() . Além disso, como
. Além disso, como ![]() , para todo
, para todo ![]() , então
, então ![]() . Em outras palavras, a sequência
. Em outras palavras, a sequência ![]() atinge
atinge ![]() em um número finito de passos, apesar de o número de passos ser em geral, extremamente grande.
em um número finito de passos, apesar de o número de passos ser em geral, extremamente grande.
Convidamos o leitor a escrever os termos das sequências ![]() e
e ![]() para a condição inicial
para a condição inicial ![]() . Para qual valor de
. Para qual valor de ![]() teremos
teremos ![]() ?
?
Qual é o valor correspondente de ![]() ? Quais são os termos seguintes das duas sequências? (ver[10]).
? Quais são os termos seguintes das duas sequências? (ver[10]).
Estamos agora preparados para examinar as sequências de Goodstein, cuja definição difere um pouco das sequências de Goodstein fracas e o modo que crescem é ainda mais espetacular. Entretanto, surpreendentemente, a estratégia para provar o seu decrescimento a zero é semelhante ao que acabamos de fazer.
4. Sequências de Goodstein
Considere novamente a representação na base 2 de 266: ![]() . Agora, escreva os expoentes na base 2:
. Agora, escreva os expoentes na base 2: ![]() ,
, ![]() . Como resultado, obtemos a expressão de 266 escrita inteiramente sem usar números maiores do que a base 2. Iniciamos a sequência de Goodstein
. Como resultado, obtemos a expressão de 266 escrita inteiramente sem usar números maiores do que a base 2. Iniciamos a sequência de Goodstein ![]() com
com ![]() . Para construir
. Para construir ![]() , substituímos todas as ocorrências de 2 na expansvo acima por 3 e subtraímos 1. Reescreva o resultado sem usar números maiores do que 3. Continue esse processo iterativamente para obter os termos sucessivos de
, substituímos todas as ocorrências de 2 na expansvo acima por 3 e subtraímos 1. Reescreva o resultado sem usar números maiores do que 3. Continue esse processo iterativamente para obter os termos sucessivos de ![]() como é mostrado na Tabela 3 (ver[11]).
como é mostrado na Tabela 3 (ver[11]).
![]()
![]()
![]()
![]()
![]()
![]()
Tabela 3.
Como você pode ver, o crescimento dos termos é espetacular e, mesmo assim, essa sequência, como todas as sequências de Goodstein, após um certo tempo começa a decrescer para finalmente convergir para ![]() (atingir
(atingir ![]() ) . A prova disso é muito similar à prova usada para as sequências de Goodstein fracas. Como naquele caso, associamos a uma sequência
) . A prova disso é muito similar à prova usada para as sequências de Goodstein fracas. Como naquele caso, associamos a uma sequência ![]() uma sequência
uma sequência ![]() substituindo cada ocorrência da base de
substituindo cada ocorrência da base de ![]() por
por ![]() .
.
Os primeiros termos da sequência ![]() correspondentes à Tabela 3 são os seguintes:
correspondentes à Tabela 3 são os seguintes:
![]()
![]()
![]()
![]()
![]()
![]()
A sequência de Goodstein ![]() de números ordinais é estritamente decrescente, o que implica que possui menor elemento. Mas, como toda vez que computamos um termo não nulo da sequência, podemos computar o termo seguinte (que é ainda menor), então, podemos concluir que o menor elemento é
de números ordinais é estritamente decrescente, o que implica que possui menor elemento. Mas, como toda vez que computamos um termo não nulo da sequência, podemos computar o termo seguinte (que é ainda menor), então, podemos concluir que o menor elemento é ![]() . Um procedimento semelhante pode ser usado para qualquer sequência de Goodstein.
. Um procedimento semelhante pode ser usado para qualquer sequência de Goodstein.
A aritmética dos números inteiros é chamada aritmética de Peano porque foi o matemático Giuseppe Peano quem primeiro formulou os seus axiomas. O que é notável na prova acima é que as ferramentas que usamos estão além da axiomática de Peano para provar um resultado totalmente formulado dentro dessa axiomática. Em outras palavras, a prova usa uma teoria geral de conjuntos que inclui os ordinais transfinitos para provar um teorema sobre números inteiros não negativos, isto é, toda sequência de Goodstein converge a ![]() . É natural perguntar se a convergência da sequência de Goodstein pode ser provada sem a utilização dos ordinais transfinitos. A resposta é não! Isso foi provado em 1982, por Lauri Kirby e Jeff Paris (ver [12]), aproximadamente 40 anos depois que as sequências foram introduzidas. Eles mostraram que se a convergência pudesse ser provada usando apenas o princípio da boa ordenação dos inteiros (isto é, dentro da aritmética de Peano) então o teorema sobre sequências Goodstein poderia ser reduzido a um teorema de Geutzen (1936), a partir do qual a consistência da aritmética de Peano poderia ser deduzida. Mas sabemos, pelo Teorema da Incompletude de Gödel (1931), que a consistência da aritmética não pode ser provada usando apenas axiomas desta aritmética. Portanto, é inútil os matemáticos gastarem energia para encontrar tal prova!
. É natural perguntar se a convergência da sequência de Goodstein pode ser provada sem a utilização dos ordinais transfinitos. A resposta é não! Isso foi provado em 1982, por Lauri Kirby e Jeff Paris (ver [12]), aproximadamente 40 anos depois que as sequências foram introduzidas. Eles mostraram que se a convergência pudesse ser provada usando apenas o princípio da boa ordenação dos inteiros (isto é, dentro da aritmética de Peano) então o teorema sobre sequências Goodstein poderia ser reduzido a um teorema de Geutzen (1936), a partir do qual a consistência da aritmética de Peano poderia ser deduzida. Mas sabemos, pelo Teorema da Incompletude de Gödel (1931), que a consistência da aritmética não pode ser provada usando apenas axiomas desta aritmética. Portanto, é inútil os matemáticos gastarem energia para encontrar tal prova!
Por outro lado, o que pode ser considerado surpreendente é que a convergência das sequências de Goodstein fracas pode ser provada dentro da aritmética de Peano. A razão essencialmente é que os termos da sequência de ordinais correspondentes são menores do que ![]() . Uma prova disso foi dada por E.Cichon, que introduziu as sequências de Goodstein fracas, em 1983,(ver [13)]. A cada termo
. Uma prova disso foi dada por E.Cichon, que introduziu as sequências de Goodstein fracas, em 1983,(ver [13)]. A cada termo ![]() de uma seqência de Goodstein fraca, podemos associar uma
de uma seqência de Goodstein fraca, podemos associar uma ![]() -upla de coeficientes da decomposição na base
-upla de coeficientes da decomposição na base ![]() e mostrar que essas m-uplas satisfazem uma boa ordem lexicográfica estritamente decrescente.
e mostrar que essas m-uplas satisfazem uma boa ordem lexicográfica estritamente decrescente.
5. Sequências de Goodstein e o jogo Hidra
Kirby e Paris mencionam em seu artigo (ver [14]) um outro processo, o jogo Hidra, que possui muitas semelhanças com as sequências de Goodstein. O nome do jogo vem da mitologia grega, de um combate entre Hércules e um animal de muitas cabeças: a Hidra (Hidra de Lerna). Cada vez que uma cabeça da Hidra é cortada, duas outras surgem em seu lugar. No jogo, a Hidra é modelada por uma árvore e as cabeças são vértices terminais ou folhas das árvores. Se Hércules corta uma cabeça que não está diretamente conectada à raiz da árvore, a aresta que chega à cabeça é eliminada, mas duas novas cabeças crescem a partir do nó localizado dois níveis abaixo da cabeça cortada. Isso pode ser feito de diversas maneiras. No exemplo de Kyrby e Paris, usado também por Hodgson ( ver [4]), se uma cabeça é cortada no passo ![]() do jogo a Hidra gera
do jogo a Hidra gera ![]() cópias da parte da árvore acima do nó do qual o ramo foi removido. No diagrama abaixo, a parte cortada é mostrada em linha tracejada, a parte que é regenerada é mostrada em vermelho e a parte nova da árvore está em azul.
cópias da parte da árvore acima do nó do qual o ramo foi removido. No diagrama abaixo, a parte cortada é mostrada em linha tracejada, a parte que é regenerada é mostrada em vermelho e a parte nova da árvore está em azul.
é possível provar que qualquer que seja a configuração das cabeças da Hidra e qualquer que seja a estratégia empregada por Hércules, ele conseguirá cortar todas as cabeças, apesar de isso acontecer após um tempo extraordinariamente longo.
Como no caso da convergência da sequência de Goodstein, a prova é baseada na relação entre árvores sucessivas e uma sequência decrescente de ordinais. Como você poderia imaginar pelos diagramas acima, as árvores tornam-se cada vez mais abertas, mas as alturas decrescem no longo prazo. Por fim, Hércules pode eliminar todas as cabeças que encontram-se em mais de um nível acima da raiz e neste momento (como ilustrado no passo 3) ele pode cortar as cabeças restantes sem gerar novas cabeças.
6. O que nos ensinam esses exemplos?
Os exemplos deste artigo são interessantes por várias razões. Eles mostram que a lógica matemática é relevante para além da metamatemática, que teoremas do tipo Teorema da Incompletude de Gödel, e objetos tais como os números transfinitos são necessários para o estudo de objetos comuns da matemática como sequências de inteiros e árvores matemáticas (grafos). Ao mostrar que uma propriedade dos números inteiros pode ser provada usando-se a teoria geral dos conjuntos mas não com a aritmética de Peano, os exemplos também chamam a nossa atenção para o cenário teórico e linguístico no qual a prova se desenvolve. Neste caso, eles mostram que a aritmética de Peano é mais fraca do que a teoria geral dos conjuntos.
Uma outra lição a partir desses exemplos é a abordagem de um problema mais difícil (convergência das sequências de Goodstein) por meio de um problema mais acessível (convergência das sequências de Goodstein fracas). Além disso, os exemplos mostram como um exemplo genérico- a sequência cujo valor inicial é 266- pode ilustrar todas as propriedades do caso geral. Os exemplos são ilustrativos também porque mostram as limitações da nossa intuição. Sequências que aparentemente tendem a infinito, convergem, pois após um número finito de etapas atingem ![]() . Finalmente, os exemplos permitem-nos ver tanto o poder quanto as limitações da tecnologia pois esta nos dá a sensação concreta de crescimento rápido dos termos da sequência, mas sua utilidade é limitada quando lidamos com a explosão numérica gerada pela definição da sequência.
. Finalmente, os exemplos permitem-nos ver tanto o poder quanto as limitações da tecnologia pois esta nos dá a sensação concreta de crescimento rápido dos termos da sequência, mas sua utilidade é limitada quando lidamos com a explosão numérica gerada pela definição da sequência.
Referências
[1] Elert, Glenn (1995-2007). The Chaos HypertextbookTM, Bodnar, M. & Ramsden P. Discrete Logistic Equation, Wolfram Demonstrations Project. Perrin, D. (2008). La suite logistique et le chaos.
[2] Lagarias, J. C. (2001) The Syracuse Problem. In Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer.
[3] Goodstein,R.L. (1944) On the Restricted Ordinal Theorem, Journal of Symbolic Logic, 9,33-41.
[4] O princípio da boa ordenação para números inteiros diz que se todo elemento em um conjunto ![]() de inteiros é maior do que um inteiro
de inteiros é maior do que um inteiro ![]() , então
, então ![]() possui o menor elemento.
possui o menor elemento.
[5] Hodgson B. (2004). Herculean of Sisyphean tasks? EMS Newsletter, March 2004, pp. 11-16.
[6] Dado um inteiro positivo ![]() , todo número inteiro positivo
, todo número inteiro positivo ![]() possui uma única decomposição na base
possui uma única decomposição na base ![]() :
: ![]() , com todos os coeficientes
, com todos os coeficientes ![]() números inteiros entre
números inteiros entre ![]() e
e ![]() e
e ![]() . Note que
. Note que ![]() . Esta é uma generalização do modo de decompor um número na base dez.
. Esta é uma generalização do modo de decompor um número na base dez.
[7] Se ![]() , então
, então ![]() ,
,![]() ,
, ![]() ,
, ![]() e
e ![]() . A partir de
. A partir de ![]() , cada termo sucessivo é igual a 1 a menos do que o anterior porque em cada caso a base é maior do que o termo precedente.
, cada termo sucessivo é igual a 1 a menos do que o anterior porque em cada caso a base é maior do que o termo precedente.
[8] Estendemos as operações de soma e o produto de inteiros para os números ordinais transfinitos, observando, entretanto que a comutatividade da soma e do produto não é preservada.
[9] Em geral, quando o termo unitário de ![]() é zero, então o menor termo de
é zero, então o menor termo de ![]() tem a forma
tem a forma ![]() , com
, com ![]() um inteiro positivo e
um inteiro positivo e ![]() . Portanto, como a base é aumentada de 1 e subtraímos 1 do resultado, a decomposição para
. Portanto, como a base é aumentada de 1 e subtraímos 1 do resultado, a decomposição para ![]() termina em
termina em ![]() . Logo, o coeficiente da menor potência da base é diminuído de 1 e o termo unitário torna-se 1 a menos que a nova base.
. Logo, o coeficiente da menor potência da base é diminuído de 1 e o termo unitário torna-se 1 a menos que a nova base.
[10] As soluções são as seguintes: ![]() quando
quando ![]() . Para obter
. Para obter ![]() , substituímos a base 31 pela base 32 e subtraímos 1. Logo
, substituímos a base 31 pela base 32 e subtraímos 1. Logo ![]() . Como a base do termo
. Como a base do termo ![]() é 32 e
é 32 e ![]() , começando com o índice 30 as sequências
, começando com o índice 30 as sequências ![]() e
e ![]() possuem exatamente os mesmos termos. Eles formam um progressão aritmética decrescente com diferença constante igual
possuem exatamente os mesmos termos. Eles formam um progressão aritmética decrescente com diferença constante igual ![]() , e segue-se que
, e segue-se que ![]() .
.
[11] The terms of {mn} shown in Table 3 were computed using http://www.wolframalpha.com.
[12] Kirby,L. e Paris, J. (1982) Accessible Independence Results for Peano Arithmetic, Bulletin of the London Mathematical Society, 14, 285-293.
[13] Cichon,E.A. (1983). A Short Proof of Two Recently Discovered Independence Results Using Recursion Theoretical Methods, Proceedings of the AMS,87,704-706.
[14] Bauer,A. Java applet for the Hydra Game ( Se o applet não funcionar em um brouser, tente em outro.)
Este post está disponível em: Inglês, Francês, Alemão, Italiano, Espanhol, Árabe, Khmer

 Português
Português 简体中文
简体中文  English
English  Français
Français  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer