 Originating authors are Michèle Artigue, Ferdinando Arzarello and Susanna Epp.
Originating authors are Michèle Artigue, Ferdinando Arzarello and Susanna Epp.
Studying the evolution of a natural phenomenon often leads to studying numerical sequences , especially their long-term behavior and whether they eventually converge. Polynomial, exponential, and logarithmic sequences are frequently encountered in secondary school, but certain other sequences with very simple definitions exhibit much more complex behavior. Examples include the chaotic sequences that arise in the study of dynamical systems (see [1]) and the Syracuse sequence (or ![]() sequence), introduced by Luther Collatz in 1937. The Syracuse sequence has challenged mathematicians for decades. Despite the huge number of values that have been computed, it is currently unknown whether the sequence is infinite or is finite and always ends in
sequence), introduced by Luther Collatz in 1937. The Syracuse sequence has challenged mathematicians for decades. Despite the huge number of values that have been computed, it is currently unknown whether the sequence is infinite or is finite and always ends in ![]() (see [2]).
(see [2]).
The sequences considered in this vignette were introduced by the British logician R. L. Goodstein in 1944 (see [3]) and exhibit a different kind of unusual behavior. Their initial values increase so rapidly that we are led to believe that they tend to infinity, but, amazingly, they always end by decreasing and ultimately reach zero. Proving this result requires a generalization of the well-ordering principle for the integers (see [4]) to transfinite numbers, but the basic idea is not hard to understand. To explain it, like Hodgson, (see [5]) we first introduce a related sequence, called a weak Goodstein sequence, which is simpler but closely related to a Goodstein sequence.
1. Weak Goodstein Sequences
As in Hodgson, we illustrate the definition of a weak Goodstein sequence by starting with the number 266. Like all positive integers, it has a unique decomposition into a sum of powers with base ![]() (see [6]):
(see [6]): ![]() . The weak Goodstein sequence with initial term
. The weak Goodstein sequence with initial term ![]() is defined as follows: To obtain
is defined as follows: To obtain ![]() copy the base
copy the base ![]() representation for
representation for ![]() but change each base
but change each base ![]() to base
to base ![]() , subtract
, subtract ![]() , and rewrite the resulting number in base
, and rewrite the resulting number in base ![]() . Thus
. Thus ![]() . To determine
. To determine ![]() start with the representation for
start with the representation for ![]() , change each base
, change each base ![]() to base
to base ![]() , subtract
, subtract ![]() , and rewrite the resulting number in base
, and rewrite the resulting number in base ![]() . Thus
. Thus ![]() . Continue generating terms of the sequence, as long as no term equals zero, by replacing the integer in the base of the previous term by the next larger integer, subtracting
. Continue generating terms of the sequence, as long as no term equals zero, by replacing the integer in the base of the previous term by the next larger integer, subtracting ![]() , and rewriting the result using the new base.
, and rewriting the result using the new base.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Table 1: Initial terms of a weak Goodstein sequence.
As you can see the terms of the sequence quickly become very large, so you might wonder if all such sequences increase as rapidly. But they do not. For instance, if ![]() , then
, then ![]() . If
. If ![]() , then
, then ![]() ,
, ![]() and
and ![]() (because the base for
(because the base for ![]() is
is ![]() and the base for
and the base for ![]() is
is ![]() ). You can check similarly that if
). You can check similarly that if ![]() , then the terms of the sequence never become larger than
, then the terms of the sequence never become larger than ![]() and reach
and reach ![]() in five steps (see [7]). However as soon as the decomposition for the initial value includes a higher power of
in five steps (see [7]). However as soon as the decomposition for the initial value includes a higher power of ![]() than
than ![]() , the initial increase in the terms is very rapid (as illustrated for
, the initial increase in the terms is very rapid (as illustrated for ![]() ), which leads to the belief that the sequence tends to infinity. How can the fact of merely subtracting
), which leads to the belief that the sequence tends to infinity. How can the fact of merely subtracting ![]() at each step counteract the enormous increase in the terms that is obtained by continually adding
at each step counteract the enormous increase in the terms that is obtained by continually adding ![]() to the base?
to the base?
And yet … let us look more carefully at the expressions in the table above. Even though successive terms of the sequence with first term ![]() increase rapidly, the exponents for the representations in successive bases tend to decrease. For instance, the exponent
increase rapidly, the exponents for the representations in successive bases tend to decrease. For instance, the exponent ![]() in
in ![]() is no longer present in
is no longer present in ![]() . Similarly, the exponent
. Similarly, the exponent ![]() in
in ![]() is replaced by a
is replaced by a ![]() in
in ![]() . And by
. And by ![]() , it is reduced to
, it is reduced to ![]() , at which point the coefficient by which it is multiplied begins to decrease. Ultimately, the exponent
, at which point the coefficient by which it is multiplied begins to decrease. Ultimately, the exponent ![]() in
in ![]() is reduced to a
is reduced to a ![]() , and the
, and the ![]() continues to be reduced in further steps. It is this characteristic, common to all the Goodstein sequences, which will allow us to show that they converge to zero. To see this, we need to bring in, as promised, the transfinite ordinal numbers.
continues to be reduced in further steps. It is this characteristic, common to all the Goodstein sequences, which will allow us to show that they converge to zero. To see this, we need to bring in, as promised, the transfinite ordinal numbers.
2. Transfinite Ordinal Numbers and Well Orderings
Ordinals:
In ordinary language, ordinal numbers are used to indicate position in a list: first, second, third, etc. Indeed, the positive integers can be used to arrange the elements of any finite set in this way. The idea of transfinite ordinal number extends the notion of ordinal number. It is due to the mathematician Georg Cantor, who developed it in a series of articles at the end of the 19th century. Because the set of integers is finite, if we imagine starting with ![]() and counting successive integers we would never finish. We can, however, imagine that there is a “number”
and counting successive integers we would never finish. We can, however, imagine that there is a “number” ![]() , that is the first number greater than every integer. Because infinitely many integers are smaller than , we call a “transfinite” ordinal number. It has a successor
, that is the first number greater than every integer. Because infinitely many integers are smaller than , we call a “transfinite” ordinal number. It has a successor ![]() , which is followed by
, which is followed by ![]() , and so forth. The smallest ordinal greater than all ordinals of the form
, and so forth. The smallest ordinal greater than all ordinals of the form ![]() , is denoted
, is denoted ![]() or
or ![]() (see [8]) and the smallest ordinal greater than all ordinals of the form
(see [8]) and the smallest ordinal greater than all ordinals of the form ![]() (where
(where ![]() is an ordinal less than
is an ordinal less than ![]() ) is denoted
) is denoted ![]() . The smallest ordinal greater than all ordinals of the form
. The smallest ordinal greater than all ordinals of the form ![]() (where
(where ![]() is an ordinal less than
is an ordinal less than ![]() ) is denoted
) is denoted ![]() .
.
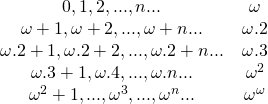
Then ![]() is followed by
is followed by ![]() ,
, ![]() , … ,
, … , ![]() ,
, ![]() , …,
, …, ![]() , … ,
, … , ![]() , …,
, …, ![]() , etc., and we define
, etc., and we define ![]() to be the smallest ordinal greater than all the sums of iterated powers of
to be the smallest ordinal greater than all the sums of iterated powers of ![]() and allow the process to continue indefinitely. In fact, all the ordinals considered thus far constitute only the beginning of the chain of ordinals because they form a countable set, that is, they can be matched up, one-for-one with the positive integers.
and allow the process to continue indefinitely. In fact, all the ordinals considered thus far constitute only the beginning of the chain of ordinals because they form a countable set, that is, they can be matched up, one-for-one with the positive integers.
Ordinals and well ordering:
A significant difference between transfinite ordinals and nonnegative integers is that each integer greater than ![]() has an immediate predecessor whereas ordinals such as
has an immediate predecessor whereas ordinals such as ![]() ,
, ![]() and
and ![]() do not. However, like the set of integers, the extended set of ordinal numbers is “well ordered” in the sense that every nonempty set of ordinals has a least element. This property is the reason we can deduce the fact that there cannot be an infinitely long strictly decreasing sequence of ordinal numbers. For suppose that such an infinite sequence exists. Let us denote it by
do not. However, like the set of integers, the extended set of ordinal numbers is “well ordered” in the sense that every nonempty set of ordinals has a least element. This property is the reason we can deduce the fact that there cannot be an infinitely long strictly decreasing sequence of ordinal numbers. For suppose that such an infinite sequence exists. Let us denote it by ![]() ,
, ![]() ,
, ![]() , …, and let
, …, and let ![]() be the set of all its terms. Given that
be the set of all its terms. Given that ![]() is nonempty, it has a least element
is nonempty, it has a least element ![]() , and so
, and so ![]() for some integer
for some integer ![]() . But since the sequence is strictly decreasing,
. But since the sequence is strictly decreasing, ![]() and so
and so ![]() is not the least element of
is not the least element of ![]() , which contradicts the supposition.
, which contradicts the supposition.
We now show how to use the ordinal numbers to prove the result about weak Goodstein sequences.
3. Proving That a Weak Goodstein Sequence Converges to Zero
To each weak Goodstein sequence ![]() , we associate a strictly decreasing sequence of ordinals
, we associate a strictly decreasing sequence of ordinals ![]() by replacing the base in every term of
by replacing the base in every term of ![]() by
by ![]() . Because the initial base of a weak Goodstein sequence is
. Because the initial base of a weak Goodstein sequence is ![]() and because the base increases by
and because the base increases by ![]() in each step, the decomposition of
in each step, the decomposition of ![]() has base
has base ![]() . Thus for the sequence associated to
. Thus for the sequence associated to ![]() , the initial terms of
, the initial terms of ![]() are shown in Table 2:
are shown in Table 2:
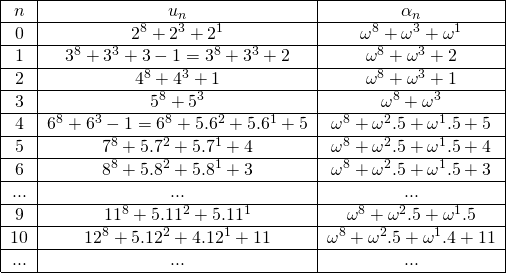
Table 2: The sequence of ordinals corresponding to a weak Goodstein sequence.
As constructed, each term of ![]() is greater than the corresponding term of
is greater than the corresponding term of ![]() , but whereas
, but whereas ![]() is increasing,
is increasing, ![]() is decreasing. The reason is that in the decomposition of
is decreasing. The reason is that in the decomposition of ![]() with base
with base ![]() , either the unit term of
, either the unit term of ![]() is nonzero or it is not. Passing from each term to the next is thus made in one of two ways:
is nonzero or it is not. Passing from each term to the next is thus made in one of two ways:
- If the unit term of
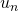 is nonzero, then because one subtracts
is nonzero, then because one subtracts  at each step, the unit term of
at each step, the unit term of 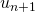 is one less than the unit term of
is one less than the unit term of 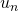 . (In Table 2, this happens in going from
. (In Table 2, this happens in going from 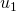 to
to 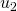 , from
, from 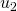 to
to 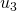 , from
, from 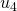 to
to 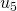 , and from
, and from 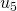 to
to 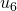 .)
.) - If the unit term of
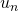 is zero, when one rewrites the decomposition in the new base, one has to break down the term of the decomposition having the smallest exponent. (In Table 2, this happens in going from
is zero, when one rewrites the decomposition in the new base, one has to break down the term of the decomposition having the smallest exponent. (In Table 2, this happens in going from 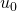 to
to 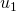 , from
, from 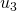 to
to 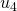 , and from
, and from 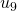 to
to 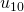 . See Table 1 for the detailed computations.) (see [9])
. See Table 1 for the detailed computations.) (see [9])
Observe that in both cases the new term of ![]() is strictly less than the preceding one.
is strictly less than the preceding one.
Now because the ordinals are well ordered, there does not exist an infinite strictly decreasing sequence of ordinals, and so there must exist an integer ![]() for which
for which ![]() . Moreover, because
. Moreover, because ![]() for all
for all ![]() ,
, ![]() must also equal
must also equal ![]() . In other words, the terms of
. In other words, the terms of ![]() reach
reach ![]() in a finite number of steps, although the number of steps may be extremely large.
in a finite number of steps, although the number of steps may be extremely large.
We invite the reader to write the terms of ![]() and
and ![]() starting with
starting with ![]() . For what value of
. For what value of ![]() is
is ![]() ? What is the value of
? What is the value of ![]() then, and what are the following terms for each of the two sequences? (see [10]).
then, and what are the following terms for each of the two sequences? (see [10]).
We are now ready to examine Goodstein sequences proper. They are defined slightly differently from weak Goodstein sequences and the nature of their increase is much more spectacular. Nonetheless, surprisingly, the strategy for proving that they eventually decrease to zero is similar to what we have just done.
4. Goodstein Sequences
Consider again the base-![]() representation for
representation for ![]() . Now write the exponents using only base
. Now write the exponents using only base ![]() :
: ![]() and
and ![]() . As a result, the entire expression for
. As a result, the entire expression for ![]() can be written entirely without using any number larger than base
can be written entirely without using any number larger than base ![]() . Let
. Let ![]() be the Goodstein sequence that starts with
be the Goodstein sequence that starts with ![]() . To construct
. To construct ![]() , replace all occurrences of
, replace all occurrences of ![]() by
by ![]() , subtract
, subtract ![]() , and rewrite the result without using any number larger than base
, and rewrite the result without using any number larger than base ![]() . Then continue process iteratively to obtain successive terms of
. Then continue process iteratively to obtain successive terms of ![]() , as shown in Table 3. (See [11]).
, as shown in Table 3. (See [11]).
![]()
![]()
![]()
![]()
![]()
![]()
Table 3.
As you see, the growth in the size of the terms is spectacular, and yet this sequence, like all Goodstein sequences, eventually starts decreasing and finally converges to ![]() . The proof is very similar to the proof for a weak Goodstein sequence. As in that case, a sequence
. The proof is very similar to the proof for a weak Goodstein sequence. As in that case, a sequence ![]() is associated to the sequence
is associated to the sequence ![]() by replacing each occurrence of each base by
by replacing each occurrence of each base by ![]() . The first few terms of
. The first few terms of ![]() are as follows:
are as follows:
![]()
![]()
![]()
![]()
![]()
![]()
The sequence ![]() of ordinal numbers is strictly decreasing, which implies that it has a least element, and, because terms continue to be computed as long as they are nonzero, the least element of the sequence is
of ordinal numbers is strictly decreasing, which implies that it has a least element, and, because terms continue to be computed as long as they are nonzero, the least element of the sequence is ![]() . Similar reasoning can be used for all the Goodstein sequences.
. Similar reasoning can be used for all the Goodstein sequences.
Ordinary integer arithmetic is often called Peano arithmetic because the 19th century Italian mathematician Giuseppe Peano first formulated its axioms. What is most notable about the elegant proof given above is that it goes outside Peano arithmetic to prove a theorem that can be stated entirely within Peano arithmetic. In other words, it uses a general theory of sets that includes transfinite ordinals to prove a theorem about nonnegative integers, namely that every Goodstein sequence converges to ![]() . It is natural to ask whether the convergence of Goodstein sequences can be proved without using transfinite ordinals. The answer is no! This was proved in 1982, approximately 40 years after the sequences were introduced, by Laurie Kirby and Jeff Paris (see [12]). They showed that if convergence could be proved using only the well-ordering principle for the integers (i.e., within Peano arithmetic), then the theorem about Goodstein sequences could be reduced to a theorem of Gentzen (1936), from which the consistency of Peano arithmetic could be deduced. But we know from the Gödel incompleteness theorem (1931) that the consistency of Peano arithmetic cannot be proved using only Peano arithmetic. It is therefore useless for mathematicians to waste their energy in trying to find such a proof!
. It is natural to ask whether the convergence of Goodstein sequences can be proved without using transfinite ordinals. The answer is no! This was proved in 1982, approximately 40 years after the sequences were introduced, by Laurie Kirby and Jeff Paris (see [12]). They showed that if convergence could be proved using only the well-ordering principle for the integers (i.e., within Peano arithmetic), then the theorem about Goodstein sequences could be reduced to a theorem of Gentzen (1936), from which the consistency of Peano arithmetic could be deduced. But we know from the Gödel incompleteness theorem (1931) that the consistency of Peano arithmetic cannot be proved using only Peano arithmetic. It is therefore useless for mathematicians to waste their energy in trying to find such a proof!
On the other hand, which may seem surprising, the fact that the weak Goodstein sequences converge to ![]() can be proved within Peano arithmetic. The reason is essentially that the terms of the associated sequence of ordinals are all less than
can be proved within Peano arithmetic. The reason is essentially that the terms of the associated sequence of ordinals are all less than ![]() . A proof was given by E. A. Cichon who introduced the weak Goodstein sequences in 1983 (see [13]). To each term
. A proof was given by E. A. Cichon who introduced the weak Goodstein sequences in 1983 (see [13]). To each term ![]() of a weak Goodstein sequence, one can correspond the
of a weak Goodstein sequence, one can correspond the ![]() -tuplet of the coefficients of the decomposition in base
-tuplet of the coefficients of the decomposition in base ![]() and show that the
and show that the ![]() -tuplets satisfy a strictly decreasing lexicographic well ordering.
-tuplets satisfy a strictly decreasing lexicographic well ordering.
5. Goodstein Sequences and the Hydra Game
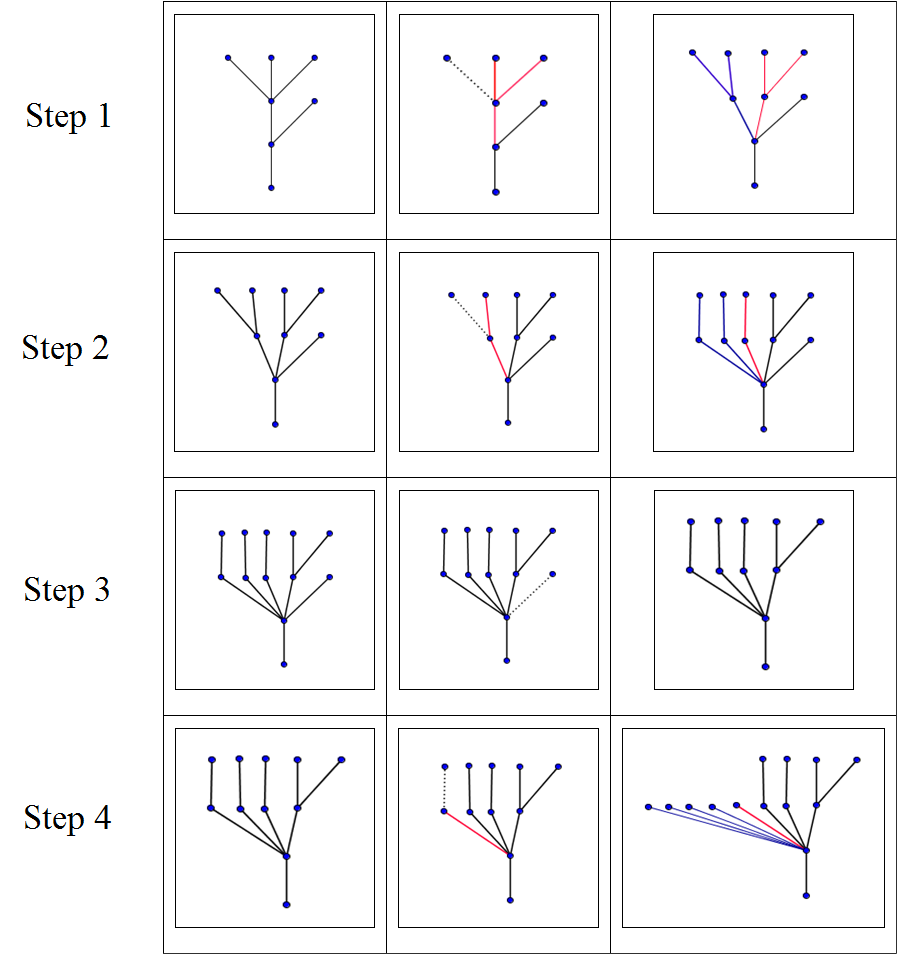
In their article, Kirby and Paris mention another process, the Hydra Game, with many similarities to the Goodstein sequences. The game (see [14]) gets its name from a description in Greek mythology of combat between Hercules and a many-headed beast: the Learnaean Hydra. Each time one of the hydra’s heads was cut off, two new ones grew in its place. In the game, the hydra is modeled by a tree, and the heads of the hydra correspond to the terminal vertices, or leaves, of the tree. If Hercules cuts a head that is not directly connected to the root of the tree, the edge leading to the head is eliminated, but the hydra grows new heads from the branch node located two levels below the head that was cut off. This can be realized in various ways. For instance, in the example given by Kirby and Paris and used again by Hodgson (see [4]), if a head is cut off in step ![]() of the game, the hydra generates
of the game, the hydra generates ![]() copies of the part of the tree above the branch node from which the head was removed. In the diagram below, the part that is cut off is shown with a dotted line, the part that is regenerated is shown in red, and the part that is newly grown is shown in blue.
copies of the part of the tree above the branch node from which the head was removed. In the diagram below, the part that is cut off is shown with a dotted line, the part that is regenerated is shown in red, and the part that is newly grown is shown in blue.
It is possible to prove that whatever the initial configuration of the hydra’s heads and whatever the strategy employed by Hercules, Hercules will always succeed in cutting all of them off, although it may take him an extraordinarily long time to finish. As for the convergence of the Goodstein sequences, the proof is based on the relationship between successive trees and a strictly decreasing sequence of ordinals. As you might guess from the diagrams shown above, the tree becomes wider and wider, but its height eventually decreases. Ultimately Hercules is able to eliminate all the heads that lie more than one level above the root, and at that point (as illustrated in step 3) he can cut off the remaining heads one by one without generating any new ones.
6. Lessons from These Examples
The examples in this vignette are interesting for several reasons. First they show that mathematical logic is relevant to more than metamathematics, that theorems such as Gödel’s incompleteness theorem and objects such as the transfinite ordinals are needed for the study of ordinary mathematical objects such as sequences of integers and mathematical trees. By showing that a property of integers can be proved within the general theory of sets but not within Peano arithmetic, the examples also draw our attention to the theoretical and linguistic framework within which proofs occur. In this case they show that Peano arithmetic is weaker than the general theory of sets.
Another lesson from these examples is the value of approaching a more difficult problem (the convergence of general Goodstein sequences) by modifying it into a more accessible one (the convergence of weak Goodstein sequences). In addition, the examples show how a generic example – a sequence whose initial value is ![]() – can illustrate all the important features of the general case. The examples are also instructive because they illustrate the limits of our intuition. Sequences that appear to tend to infinity do not in fact do so; they ultimately start decreasing and converge to
– can illustrate all the important features of the general case. The examples are also instructive because they illustrate the limits of our intuition. Sequences that appear to tend to infinity do not in fact do so; they ultimately start decreasing and converge to ![]() in a finite number of steps. Finally, the examples enable us to see both the power and the limits of technology because technology gives us a concrete sense for the rapid increase in the terms of the sequence, but it is of limited use when faced with the numerical explosion generated by the sequence definition.
in a finite number of steps. Finally, the examples enable us to see both the power and the limits of technology because technology gives us a concrete sense for the rapid increase in the terms of the sequence, but it is of limited use when faced with the numerical explosion generated by the sequence definition.
References
[1] Elert, Glenn (1995-2007). The Chaos HypertextbookTM, Bodnar, M. & Ramsden P. Discrete Logistic Equation, Wolfram Demonstrations Project. Perrin, D. (2008). La suite logistique et le chaos.
[2] Lagarias, J. C. (2001) The Syracuse Problem. In Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer.
[3] Goodstein, R. L. (1944). On the Restricted Ordinal Theorem, Journal of Symbolic Logic, 9, 33-41.
[4] The well ordering principle for the integers states that if every element in a set ![]() of integers is greater than some integer
of integers is greater than some integer ![]() , then
, then ![]() has a least element.
has a least element.
[5] Hodgson B. (2004). Herculean of Sisyphean tasks? EMS Newsletter, March 2004, pp. 11-16.
[6] Given an integer ![]() with
with ![]() , every positive integer
, every positive integer ![]() has a unique decomposition in base b:
has a unique decomposition in base b: ![]() , where all the
, where all the ![]() are integers between
are integers between ![]() and
and ![]() and
and ![]() . Note that
. Note that ![]() . This is a generalization of the way we decompose numbers using base ten.
. This is a generalization of the way we decompose numbers using base ten.
[7] If ![]() , then
, then ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Starting with
. Starting with ![]() , each successive term is one less than the previous term because in each case the base is larger than the previous term.
, each successive term is one less than the previous term because in each case the base is larger than the previous term.
[8] We extend the sum and product operations from the integers to the transfinite ordinal numbers, noting, however, that commutativity of addition and multiplication are not preserved.
[9] In general, when the unit term of ![]() is zero, then the smallest term of
is zero, then the smallest term of ![]() has the form
has the form ![]() , where
, where ![]() is a positive integer and
is a positive integer and ![]() . Thus, because the base is increased by
. Thus, because the base is increased by ![]() and because
and because ![]() is subtracted from the result, the decomposition for
is subtracted from the result, the decomposition for ![]() ends in
ends in ![]() .
.
So the coefficient of the smallest power of the base is reduced by ![]() and the unit term becomes one less than the new base.
and the unit term becomes one less than the new base.
[10] The responses are as follows: ![]() when
when ![]() , and thus
, and thus ![]() . To obtain
. To obtain ![]() , replace the base
, replace the base ![]() by the base
by the base ![]() and subtract
and subtract ![]() . Hence
. Hence ![]() , and so
, and so ![]() . Given that the base of
. Given that the base of ![]() is
is ![]() and that
and that ![]() , starting from the subscript
, starting from the subscript ![]() the sequences
the sequences ![]() and
and ![]() have exactly the same terms. They form a decreasing arithmetic sequence with constant difference
have exactly the same terms. They form a decreasing arithmetic sequence with constant difference ![]() , from which it follows that
, from which it follows that ![]() .
.
[11] The terms of {mn} shown in Table 3 were computed using http://www.wolframalpha.com.
[12] Kirby, L. and Paris, J. (1982). Accessible Independence Results for Peano Arithmetic, Bulletin of the London Mathematical Society, 14, 285-293.
[13] Cichon, E. A. (1983). A Short Proof of Two Recently Discovered Independence Results Using Recursion Theoretic Methods, Proc. Amer. Math. Soc., 87, 704-706.
[14] Bauer, A. Java applet for the Hydra Game. (If the applet fails to work in one browser, try it in another.)

Excellent maths challenge; certainly there are some extension students (secondary) who will take an interest in this.
However, may I suggest that the notation of the multiplication operator be changed to either comply with European standards or with ours. As it’s printed here, the multiplication can be and will be mistaken for a decimal point, with the consequence that the students will give up.
I have two questions here
1) I am not convinced that the least element αm of the sequence of ordinals that correspond to the (weak) Goodstein sequence should be zero. From the well ordering of the ordinals indeed there is a least element for the sequence αm , and for all k>m αk=αm. What is the argument that it should be 0, not another fixed ordinal? E.g. ω, so that in the next step the increase of the base by one, and the minus one cancel out given always the same natural number , corresponding to ω?
The second question is
2) The sequence αm seems to me that it can very well be constructed without the theory of ordinlas. E. g. we may use a variable x instead of ω, and polynomilas over x, instead of expressions of ω. Then well-order these polynomials (x^n<x^(n+1), nxn for every n , etc), in similar way as the ordinals (or in a appropriate symbolic lexicographic order, as tuples of naturals), and apply the same argument.
Why then such a proof with well ordered polynomials would not be a proof within the Peano arithmetic?
Le blog sur les suites de Goodstein explique qu’une preuve de terminaison de l’algorithme est basée sur la considération d’une suite d’ordinaux strictement décroissante qui commence à l’ordinal epsilon_0 et ne s’arrête que si elle atteint . Elle doit donc terminer un jour.
. Elle doit donc terminer un jour.
Or on dispose d’une preuve convaincante (constructive) que la relation d’ordre sur N, que l’on peut décrire explicitement, qui correspond à l’ordinal epsilon_0, est bien une relation de bon ordre au sens constructif*
* une relation d’ordre total est un bon ordre si toute suite décroissante (au sens large) possède deux termes consécutifs égaux
La preuve de terminaison donnée par Goodstein est donc acceptable constructivement, sans recours à la logique du tiers exclu, ni aux infinis actuels de Cantor, ni aux axiomes étranges de ZF.
Il n’y a pas ici de différence structurelle entre
– le fait de pratiquer la récurrence sur N sans se soucier de savoir s’il y a un infini actuel à la clé (ce dont ni les Grecs, ni Pascal, ni Poincaré ne se soucient lorsqu’ils expliquent le raisonnement par récurrence),
– et le fait de pratiquer la récurrence sur l’ordinal epsilon_0 sans se soucier de savoir s’il y a un infini actuel à la clé (c’est toujours N en fait!)
Beaucoup de théorèmes démontrés dans ZF concernant les ordinaux ne sont plus valables en maths constructives. Mais ce sont justement les théorèmes qui ne servent à rien en pratique. Les théorèmes utiles en pratique, comme « epsilon_0 est un bon ordre », eux, sont démontrables constructivement.
Je rappelle que Gentzen a montré pour l’essentiel que la cohérence de Peano est une affirmation qui équivaut à « epsilon_0 est un bon ordre ».
Une remarque sur le fait que la théorie des ensembles serait l’ultime recours pour démontrer que certains ordres totaux sur N sont des bons ordres.
C’est vraiment très étrange, car la théorie des ensembles ne peut certainement pas être démontrée non contradictoire. Donc la preuve invoquée via ZF ne prouve absolument rien.
Accepter la preuve constructive que epsilon_0 est un bon ordre n’est quand même pas grand chose par comparaison à admettre que ZF soit consistante.
Plus généralement, je recommande l’article suivant:
Per Martin-Löf: The Hilbert-Brouwer controversy resolved? dans: One
hundred years of intuitionism (1907-2007), (Cerisy), (Mark Van Atten & al.,
editors) Publications des Archives Henri Poincaré, Birkhäuser Basel, (2008),
pp. 243-256.
Henri LOMBARDI
e mail : Henri.Lombardi@univ-fcomte.fr
page web http://hlombardi.free.fr/
Pingback: Recurrence and induction | Klein Project Blog