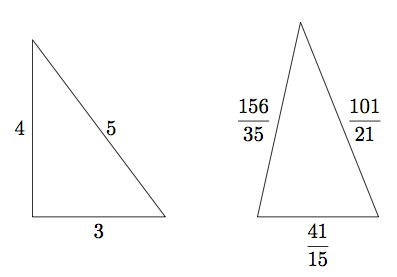 Autor do texto original : William McCallum.
Autor do texto original : William McCallum.
Se dois triângulos têm mesma área e mesmo perímetro, serão eles necessariamente congruentes? Vamos ver que a resposta é não. Por exemplo, o triângulo de lados ![]() ,
, ![]() e
e ![]() tem a mesma área e mesmo perímetro que o triângulo de lados
tem a mesma área e mesmo perímetro que o triângulo de lados ![]() ,
, ![]() e
e ![]() .
.
O perímetro de ambos os triângulos é ![]() :
:
![]()
Surpreendentemente, os dois triângulos também têm a mesma área. A área do triângulo retângulo é ![]() . Para encontrar a área do outro triângulo, usamos a fórmula de Heron, segundo a qual a área A de um triângulo de lados
. Para encontrar a área do outro triângulo, usamos a fórmula de Heron, segundo a qual a área A de um triângulo de lados ![]() ,
, ![]() e
e ![]() é dada por
é dada por
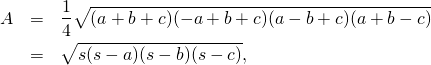
sendo ![]() o semiperímetro do triângulo. Um cálculo rápido usando essa fórmula, mostra que a área do segundo triângulo também é
o semiperímetro do triângulo. Um cálculo rápido usando essa fórmula, mostra que a área do segundo triângulo também é ![]() .
.
O espaço dos triângulos
Como encontrar exemplos assim? O segredo está em encontrar o caminho certo para representar o espaço de todos os triângulos. Há vários caminhos possíveis. Um caminho é representar um triângulo pelo terno ![]() formado pelos comprimentos dos três lados, em alguma ordem. Desse modo representamos um triângulo por um ponto no espaço tridimensional. Nem todo ponto corresponde a um triângulo; por exemplo, todas as coordenadas devem ser positivas. Você saberia dar outras restrições?
formado pelos comprimentos dos três lados, em alguma ordem. Desse modo representamos um triângulo por um ponto no espaço tridimensional. Nem todo ponto corresponde a um triângulo; por exemplo, todas as coordenadas devem ser positivas. Você saberia dar outras restrições?
Existe outro caminho para colocar coordenadas no espaço dos triângulos, usando ângulos em vez de comprimentos. Todo triângulo tem um círculo inscrito, e o raio ![]() do círculo tem uma relação simples com a área
do círculo tem uma relação simples com a área ![]() do triângulo e seu semiperímetro
do triângulo e seu semiperímetro ![]() , a saber:
, a saber:
![]()
Para ver porque isso é verdade, trace perpendiculares do centro do círculo aos lados do triângulo, como na figura 2, lado esquerdo. Essas perpendiculares formam as alturas de três triângulos menores que têm um vértice no centro do círculo inscrito e cujas bases são os lados do triângulo grande. Somando as áreas desses triângulos, obtemos ![]() .
.

Figura 2: Parametrizando o espaço dos triângulos
Essa equação nos diz que se dois triângulos tiverem a mesma área e o mesmo perímetro, os raios de seus círculos inscritos também serão iguais. Então se estivermos procurando dois triângulos nessas condições, nós os encontraremos dentre todos os triângulos circunscritos a um círculo fixo. Em vez de usar comprimentos para descrever esses triângulos, usaremos os ângulos formados pelos três raios no centro do círculo inscrito, como na figura 2, lado direito.
Parametrizando triângulos de área e perímetro constantes
Dentro do espaço dos triângulos podemos encontrar curvas correspondendo a uma família inteira de triângulos, todos eles com mesma área ![]() e mesmo semiperímetro s. Inicialmente, vamos escrever
e mesmo semiperímetro s. Inicialmente, vamos escrever ![]() em função dos ângulos
em função dos ângulos ![]() ,
, ![]() e
e ![]() e do raio
e do raio ![]() do círculo inscrito, como veremos a seguir. Os raios e as retas que unem os vértices do triângulo ao centro do círculo inscrito particionam esse triângulo em seis triângulos retângulos. Observando que as retas que unem os vértices do triângulo ao centro do círculo bissectam os ângulos do triângulo grande, esses triângulos retângulos ocorrem em pares congruentes. Escolhendo o comprimento da base de um dos triângulos de cada par e somando, obtemos:
do círculo inscrito, como veremos a seguir. Os raios e as retas que unem os vértices do triângulo ao centro do círculo inscrito particionam esse triângulo em seis triângulos retângulos. Observando que as retas que unem os vértices do triângulo ao centro do círculo bissectam os ângulos do triângulo grande, esses triângulos retângulos ocorrem em pares congruentes. Escolhendo o comprimento da base de um dos triângulos de cada par e somando, obtemos:
![]()
Essa equação, juntamente com ![]() , permite concluir que se a área
, permite concluir que se a área ![]() e o semiperímetro
e o semiperímetro ![]() são constantes, então a soma das tangentes também é constante :
são constantes, então a soma das tangentes também é constante :
(1) ![]()
A seguir, transformamos essa condição numa equação que define uma curva no plano.
Sejam ![]() ,
, ![]() , e
, e ![]() . Como
. Como ![]() , temos
, temos
![]()
e, assim
![]()
Então, se ![]() for a constante
for a constante ![]() a equação (1), para
a equação (1), para ![]() fixo, fica:
fixo, fica:
(2) ![]()
(3) ![]()
Todo triângulo de área ![]() e semiperímetro s determina um ponto desta curva e todo ponto desta curva, numa certa região do plano, corresponde a um triângulo. A região corresponde a ângulos que realmente funcionam na Figura 2, isto é, ângulos que satisfazem
e semiperímetro s determina um ponto desta curva e todo ponto desta curva, numa certa região do plano, corresponde a um triângulo. A região corresponde a ângulos que realmente funcionam na Figura 2, isto é, ângulos que satisfazem ![]() e
e ![]() , que corresponde à região
, que corresponde à região ![]() ,
, ![]() e
e ![]() (pois
(pois ![]() ).
).
A figura a seguir mostra essa curva para ![]() , valor que corresponde ao triângulo
, valor que corresponde ao triângulo ![]() ,
, ![]() e
e ![]() . Cada ponto da componente dessa curva, no primeiro quadrante, corresponde a um triângulo; os comprimentos dos lados do triângulo são
. Cada ponto da componente dessa curva, no primeiro quadrante, corresponde a um triângulo; os comprimentos dos lados do triângulo são ![]() ,
, ![]() e
e ![]() . Em particular, os pontos
. Em particular, os pontos ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() correspondem ao triângulo de lados
correspondem ao triângulo de lados ![]() ,
, ![]() e
e ![]() , com os lados tomados em ordens diferentes. Essa figura é interativa: veja o que acontece para alguns outros pontos da curva ou outros valores para a área e o perímetro!
, com os lados tomados em ordens diferentes. Essa figura é interativa: veja o que acontece para alguns outros pontos da curva ou outros valores para a área e o perímetro!
Encontrando pontos da curva
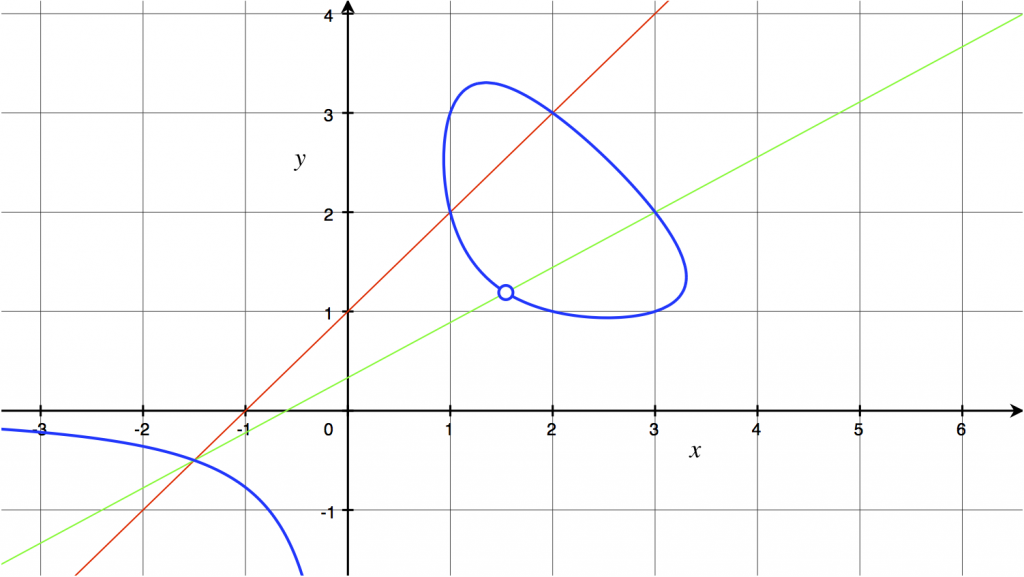
Figura 3: Curva parametrizando triângulos de perímetro 12 e área 6.
Como a curva da Figura 3 é definida por uma equação de grau 3, podemos encontrar pontos dessa curva usando o método de tangentes e secantes (método das duas secantes). Dois pontos da curva determinam uma secante que corta a curva em mais um ponto; encontrar esse ponto consiste em resolver uma equação do terceiro grau em ![]() , da qual já conhecemos duas raízes. Como já conhecemos
, da qual já conhecemos duas raízes. Como já conhecemos ![]() pontos da curva, existem muitas possibilidades para secantes e gerando mais pontos geram-se mais possibilidades. De fato, a curva tem uma infinidade de pontos com coordenadas racionais. O procedimento com duas secantes, ilustrado na Figura 3, nos leva ao ponto
pontos da curva, existem muitas possibilidades para secantes e gerando mais pontos geram-se mais possibilidades. De fato, a curva tem uma infinidade de pontos com coordenadas racionais. O procedimento com duas secantes, ilustrado na Figura 3, nos leva ao ponto ![]() (assinalado com um círculo) que corresponde ao triângulo de lados
(assinalado com um círculo) que corresponde ao triângulo de lados ![]() ,
, ![]() e
e ![]() .
.
O procedimento usando secantes funciona para qualquer curva cúbica no plano; tais curvas são chamadas curvas elípticas (não porque as curvas são elipses, mas porque elas surgem no estudo de certa classe de funções complexas chamadas funções elípticas). O procedimento usando secantes permite definir uma estrutura de grupo no conjunto dos pontos racionais de uma curva elíptica (isto é, pontos cujas coordenadas são números racionais).
O estudo de curvas elípticas é uma área central de pesquisa em teoria dos números, com aplicações em esquemas criptográficos que estão por trás de transações financeiras seguras na web. Curvas elípticas têm papel central na demonstração do Último Teorema de Fermat.
A história descrita neste artigo, começando com a matemática do ensino básico e terminando em áreas de pesquisa, mostra a extraordinária unidade da matemática. Ao longo do caminho encontramos uma ideia fundamental da matemática moderna: a ideia de resolver um problema a respeito de um tipo particular de objeto (triângulos com área 6 e perímetro 12, por exemplo), colocando o objeto num espaço mais geral (o espaço de todos os triângulos) e encontrando o caminho certo de parametrizar esse espaço.
Este post está disponível em: Chinês, Inglês, Francês, Alemão, Italiano, Espanhol, Árabe, Khmer

 Português
Português 简体中文
简体中文  English
English  Français
Français  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer