 Autor do original: Christiane Rousseau.
Autor do original: Christiane Rousseau.
Neste artigo, começando com um pequeno jogo, vamos descobrir um dos mais potentes teoremas da matemática, a saber, o teorema do ponto fixo de Banach. Esse teorema tem aplicações maravilhosas tanto na matemática quanto em outras áreas. Na terceira parte deste artigo, veremos uma aplicação fascinante em compressão de imagens.
Vamos começar nosso jogo olhando mais de perto a famosa tampa de uma caixa de A Vaca Que Ri. (NT. A Vaca Que Ri é a marca de um queijo fundido comercializado em vários países, Brasil inclusive.)
O brinco na orelha direita da Vaca é novamente uma tampa da caixa de A Vaca Que Ri. A cada ponto da tampa pode-se associar o ponto correspondente no brinco da orelha direita. Obtém-se assim, com certeza, uma função da tampa nela mesma que chamaremos de ![]() . Por exemplo, associa-se a ponta do queixo da Vaca à ponta do queixo da pequena vaca do brinco. Associa-se o centro do olho direito da Vaca ao centro do olho direito da pequena vaca do brinco, etc. Eis agora a questão: Existe um ponto que é enviado nele mesmo por esse procedimento? Tal ponto, se existir, será chamado ponto fixo. Se um ponto fixo existir, ele não será nenhum dos pontos mencionados anteriormente. Além do mais, se um ponto fixo existir, ele deverá estar no brinco direito. Mas esse brinco direito é enviado para o brinco direito da vaca pequena, etc. Visualmente, percebe-se que esses brincos direitos encaixados parecem convergir para um ponto, que chamaremos de
. Por exemplo, associa-se a ponta do queixo da Vaca à ponta do queixo da pequena vaca do brinco. Associa-se o centro do olho direito da Vaca ao centro do olho direito da pequena vaca do brinco, etc. Eis agora a questão: Existe um ponto que é enviado nele mesmo por esse procedimento? Tal ponto, se existir, será chamado ponto fixo. Se um ponto fixo existir, ele não será nenhum dos pontos mencionados anteriormente. Além do mais, se um ponto fixo existir, ele deverá estar no brinco direito. Mas esse brinco direito é enviado para o brinco direito da vaca pequena, etc. Visualmente, percebe-se que esses brincos direitos encaixados parecem convergir para um ponto, que chamaremos de ![]() , e
, e ![]() é um candidato para nossa solução.
é um candidato para nossa solução.
Comecemos agora com um ponto qualquer, por exemplo, a extremidade do queixo da vaca, que chamaremos de ![]() . O ponto
. O ponto ![]() é enviado para
é enviado para ![]() , que é a extremidade do queixo da pequena vaca no brinco direito. O ponto
, que é a extremidade do queixo da pequena vaca no brinco direito. O ponto ![]() é enviado para
é enviado para ![]() , que é a extremidade do queixo da pequena vaca no brinco direito, etc. Observamos três fatos:
, que é a extremidade do queixo da pequena vaca no brinco direito, etc. Observamos três fatos:
- Podemos continuar esse procedimento indefinidamente e construir assim uma sequência
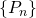 , com
, com 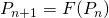 .
.
- Visualmente, é apenas um número finito de pontos que parecem ser distintos, os outros são indistinguíveis. Certamente pode-se dar um zoom e ver mais pontos. Mas, independentemente da potência do zoom, distinguiremos apenas um número finito de pontos, os outros parecerão sobrepostos
- Essa sequência parece convergir para o ponto
 , definido anteriormente.
, definido anteriormente.
Se tivéssemos considerado outro ponto, ![]() e construído a sequência
e construído a sequência ![]() , com
, com ![]() , veríamos que a sequência
, veríamos que a sequência ![]() também parece convergir para o ponto
também parece convergir para o ponto ![]() . De fato, pode-se observar que isso ocorre porque o conjunto unitário
. De fato, pode-se observar que isso ocorre porque o conjunto unitário ![]() é o conjunto intersecção de todos os brincos encaixados e seu diâmetro tende a
é o conjunto intersecção de todos os brincos encaixados e seu diâmetro tende a ![]() .
.
O que o teorema do ponto fixo de Banach vai nos dizer? Vai nos dizer que, de fato, a função ![]() tem um único ponto fixo, isto é, existe um único ponto
tem um único ponto fixo, isto é, existe um único ponto ![]() do plano tal que
do plano tal que ![]() . Além disso, o teorema estabelecerá que se considerarmos um ponto
. Além disso, o teorema estabelecerá que se considerarmos um ponto ![]() qualquer e construirmos a sequência
qualquer e construirmos a sequência ![]() , com
, com ![]() , a sequência
, a sequência ![]() vai convergir para
vai convergir para ![]() .
.
Mas por quê? Isso aconteceria para qualquer função ![]() ? É claro que não. Por exemplo, uma translação no plano não tem pontos fixos. E a função
? É claro que não. Por exemplo, uma translação no plano não tem pontos fixos. E a função ![]() tem dois pontos fixos :
tem dois pontos fixos : ![]() . A função
. A função ![]() do nosso jogo tem uma propriedade especial. Ela é uma contração. De fato, sua imagem é muito menor do que seu domínio. Se dois pontos
do nosso jogo tem uma propriedade especial. Ela é uma contração. De fato, sua imagem é muito menor do que seu domínio. Se dois pontos ![]() e
e ![]() estiverem a certa distância um do outro, suas imagens
estiverem a certa distância um do outro, suas imagens ![]() e
e ![]() estarão mais próximas uma da outra do que
estarão mais próximas uma da outra do que ![]() e
e ![]() . Essa afirmação tem sentido porque em
. Essa afirmação tem sentido porque em ![]() podemos medir a distância entre dois elementos. Isso acontece porque
podemos medir a distância entre dois elementos. Isso acontece porque ![]() é um espaço métrico. O fato de
é um espaço métrico. O fato de ![]() ser uma contração garante que ao construirmos a sequência
ser uma contração garante que ao construirmos a sequência ![]() , qualquer que seja o elemento de partida escolhido (se vamos olhar a sequência de longe, de perto, ou através de um microscópio, ou através de um microscópio eletrônico), após algum
, qualquer que seja o elemento de partida escolhido (se vamos olhar a sequência de longe, de perto, ou através de um microscópio, ou através de um microscópio eletrônico), após algum ![]() , que depende desse elemento de partida, todos os elementos
, que depende desse elemento de partida, todos os elementos ![]() ,
, ![]() , da sequência tornar-se-ão indistinguíveis. Dois elementos são distinguíveis se a distância ente eles estiver acima de certo valor. Veremos na próxima seção que uma sequência com essa propriedade chama-se sequência de Cauchy. Em
, da sequência tornar-se-ão indistinguíveis. Dois elementos são distinguíveis se a distância ente eles estiver acima de certo valor. Veremos na próxima seção que uma sequência com essa propriedade chama-se sequência de Cauchy. Em ![]() , toda sequência de Cauchy é uma sequência convergente. Dizemos que
, toda sequência de Cauchy é uma sequência convergente. Dizemos que ![]() é um espaço métrico completo.
é um espaço métrico completo.
1. O teorema do ponto fixo de Banach
Temos, agora, todos os ingredientes necessários para o caso geral e podemos enunciar o teorema.
Teorema (do ponto fixo de Banach). Seja ![]() um espaço métrico completo no qual a distância entre dois pontos
um espaço métrico completo no qual a distância entre dois pontos ![]() e
e ![]() é representada por
é representada por ![]() . Seja
. Seja ![]() uma contração, isto é, existe
uma contração, isto é, existe ![]() tal que para todos
tal que para todos ![]() , tem-se
, tem-se
![]()
Então ![]() tem um único ponto fixo, isto é, existe um único
tem um único ponto fixo, isto é, existe um único ![]() tal que
tal que ![]() .
.
Vamos definir todos os termos que aparecem nessa afirmação. Essa parte é mais formal e pode ser deixada de lado se você preferir concentrar-se nas fascinantes aplicações.
Sabemos o que é distância entre dois pontos ![]() e
e ![]() em
em ![]() . Como generalizar esse conceito para um conjunto
. Como generalizar esse conceito para um conjunto ![]() ?
?
Definição. Distância em um conjunto ![]() é uma função
é uma função ![]() satisfazendo
satisfazendo
- Para todo
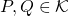 ,
, 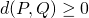 ;
;
-
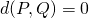 se, e somente se, if
se, e somente se, if 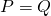 ;
;
- Para todo
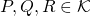 ,
, 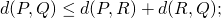 (desigualdade triangular).
(desigualdade triangular).
Sabemos que essas condições são satisfeitas pela distância euclidiana usual em ![]() .
.
Recordemos agora a definição de sequência de Cauchy, que é a formalização do conceito de uma sequência que, pouco importando o grau de precisão escolhido, após um número finito de elementos, todos os demais tornam-se indistinguíveis. Vamos recordar também a definição de sequência convergente.
Definição.
- Uma sequência
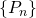 de elementos de um espaço métrico
de elementos de um espaço métrico  é uma sequência de Cauchy se, para todo
é uma sequência de Cauchy se, para todo 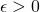 , existe
, existe 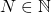 tal que para todos
tal que para todos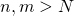 , then
, then
![Rendered by QuickLaTeX.com \[d(P_n,P_m)<\epsilon.\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-1c97f4794c43d7a0ea39241b9d7b70f0_l3.png)
- Uma sequência
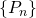 de elementos de um espaço métrico
de elementos de um espaço métrico 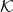 converge para um limite
converge para um limite 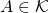 se, para todo
se, para todo 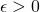 , existe
, existe 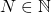 tal que para todo
tal que para todo 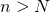 ,
,
![Rendered by QuickLaTeX.com \[d(P_n,A)<\epsilon.\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-15d19b7399d98032c767b201bb2322a3_l3.png)
Definição. Um espaço métrico ![]() é um espaço métrico completo se toda sequência de Cauchy
é um espaço métrico completo se toda sequência de Cauchy ![]() é um espaço métrico completo se toda sequência de Cauchy
é um espaço métrico completo se toda sequência de Cauchy ![]() converge para um elemento
converge para um elemento ![]() de
de ![]() .
.
Como se demonstra o teorema do ponto fixo de Banach ? É fácil provar a unicidade do ponto fixo. De fato, suponha que ![]() e
e ![]() sejam dois pontos fixos. Então
sejam dois pontos fixos. Então ![]() e
e ![]() . Além disso, se
. Além disso, se ![]() é uma contração, então
é uma contração, então
![]()
Portanto, ![]() . A única solução é
. A única solução é ![]() , o que acarreta
, o que acarreta ![]() .
.
Quanto à existência, a ideia da demonstração é igualmente simples: nós já a encontramos no jogo de A Vaca que Ri! Escolhemos um ponto qualquer ![]() e construímos (como antes) a sequência
e construímos (como antes) a sequência ![]() , com
, com ![]() . Essa é uma sequência de Cauchy e seu limite é um ponto fixo. ( É claro que provar essas duas afirmações requer algum trabalho, mas aqui vamos omitir os detalhes técnicos. O que importa é que a demonstração é a mesma quer no caso geral de um espaço métrico complicado, quer no caso simples de
. Essa é uma sequência de Cauchy e seu limite é um ponto fixo. ( É claro que provar essas duas afirmações requer algum trabalho, mas aqui vamos omitir os detalhes técnicos. O que importa é que a demonstração é a mesma quer no caso geral de um espaço métrico complicado, quer no caso simples de ![]() .)
.)
A ideia da demonstração não é apenas simples e intuitiva, mas é também muito potente. Ela nos fornece uma maneira de construir numericamente o ponto fixo ![]() . Isso explica o fato de muitas aplicações desse teorema serem encontradas tanto em questões teóricas como em suas aplicações.
. Isso explica o fato de muitas aplicações desse teorema serem encontradas tanto em questões teóricas como em suas aplicações.
2. Aplicações em Análise Matemática
Uma das aplicações teóricas muito importantes do teorema do ponto fixo de Banach é a demonstração da existência e unicidade de soluções de equações diferenciais suficientemente regulares. Nessa aplicação, o espaço métrico completo ![]() é um conjunto de funções, e a função
é um conjunto de funções, e a função ![]() transforma uma função em outra função (dizemos muitas vezes que
transforma uma função em outra função (dizemos muitas vezes que ![]() é um operador). O truque consiste em mostrar que uma solução da equação diferencial, se existir, é um ponto fixo do operador
é um operador). O truque consiste em mostrar que uma solução da equação diferencial, se existir, é um ponto fixo do operador ![]() .
.
Talvez você tenha estudado equações diferenciais simples e aprendido artifícios para encontrar fórmulas para as soluções. Bem, essas equações diferenciais são exceções, pois para a maioria das equações diferenciais não existem fórmulas para a solução. Daí a importância de um teorema que garanta a existência de uma solução. Não lhe deve causar espanto que para a solução da maioria das equações diferenciais nenhuma fórmula pode ser dada. De fato, considere a simples equação diferencial
![]()
Sua solução é dada por
![]()
Você deve lembrar que no seu curso de Probabilidade ou de Estatística lhe contaram que não existe uma fórmula para a primitiva da função ![]() , explicando, assim, porque é necessário trabalhar com tabelas quando se estuda a distribuição normal.
, explicando, assim, porque é necessário trabalhar com tabelas quando se estuda a distribuição normal.
3. Aplicação à compressão de imagens
A melhor maneira de armazenar uma imagem na memória é armazenar a cor de cada pixel. Há dois problemas com esse método:
- Exige uma quantidade enorme de memória.
- Se tentarmos ampliar a imagem, para usá-la, por exemplo, num poster grande, os pixeis tornam-se quadrados grandes e não teremos suficientes informações para preencher os detalhes nesses quadrados.
Qual é o princípio da compressão de imagens? É codificar menos informação do que a imagem original, mas fazê-lo de uma maneira inteligente, de modo que os olhos não percebam que a imagem observada está deteriorada. A internet aumentou a necessidade de bons sistemas compressão de imagens. Imagens, de fato, diminuem significativamente a velocidade de navegação na internet.  Portanto, para navegar na internet, é bom ter imagens codificadas em arquivos tão pequenos quanto possível. Quando você olha para a imagem na tela do seu computador você não percebe que ela foi deteriorada. Mas se você tentar ampliar essa imagem, ou imprimi-la num poster, você imediatamente percebe que a resolução da imagem é ruim.
Portanto, para navegar na internet, é bom ter imagens codificadas em arquivos tão pequenos quanto possível. Quando você olha para a imagem na tela do seu computador você não percebe que ela foi deteriorada. Mas se você tentar ampliar essa imagem, ou imprimi-la num poster, você imediatamente percebe que a resolução da imagem é ruim.
Existem vários procedimentos de compressão de imagens e o mais comuns é o JPEG, que se tronou padrão para imagens digitais. A codificação de uma imagem em formato JPEG também é um algoritmo matemático.
 Neste artigo vamos nos concentrar num outro método, que tem permanecido mais experimental. Esse método, introduzido por Barnsley, foi chamado sistema de funções iteradas. A ideia subjacente ao método é aproximar uma imagem por objetos geométricos. Para ter um número suficiente de objetos disponíveis, não nos limitaremos aos objetos geométricos usuais como retas e curvas, mas usaremos também figuras fractais complexas como a samambaia e o tapete de Sierpinski (veja as figuras à esquerda)
Neste artigo vamos nos concentrar num outro método, que tem permanecido mais experimental. Esse método, introduzido por Barnsley, foi chamado sistema de funções iteradas. A ideia subjacente ao método é aproximar uma imagem por objetos geométricos. Para ter um número suficiente de objetos disponíveis, não nos limitaremos aos objetos geométricos usuais como retas e curvas, mas usaremos também figuras fractais complexas como a samambaia e o tapete de Sierpinski (veja as figuras à esquerda)
 Vamos explicar a ideia do processo de compressão no tapete de Sierpinski, à esquerda. A priori, parece ser um objeto complicado. Como armazená-lo na memória de um computador de uma maneira econômica? A melhor maneira é armazenar um programa que o reconstruirá quando for necessário.
Vamos explicar a ideia do processo de compressão no tapete de Sierpinski, à esquerda. A priori, parece ser um objeto complicado. Como armazená-lo na memória de um computador de uma maneira econômica? A melhor maneira é armazenar um programa que o reconstruirá quando for necessário.
E para construir esse programa precisamos compreender o que caracteriza esse objeto geométrico. Observemos o tapete de Sierpinski: ele é a reunião de três tapetes de Sierpinski (isto é, três cópias de si mesmo) que têm a metade do seu tamanho (em largura e altura). De fato, começando com um tapete de Sierpinski, podemos construir um segundo tapete com o seguinte procedimento:
- A partir do vértice inferior esquerdo, encolhemos o tapete de Sierpinski, até sua metade.
- Fazemos uma segunda cópia desse meio tapete de Sierpinski e a colamos à direita da primeira.
- Fazemos uma terceira cópia desse meio tapete de Sierpinski e a colamos acima das outras duas.
A segunda figura que construímos é idêntica ao nosso o tapete de Sierpinski inicial. Portanto o tapete de Sierpinski é o ponto fixo do processo.
Vamos escrever isso em termos matemáticos. Observe que o comprimento da base do tapete de Sierpinski é igual à sua altura. Então, podemos escolher eixos com origem no canto inferior esquerdo do tapete de Sierpinski e unidades nos eixos tais que a base e a altura tenham ambos comprimento ![]() .
.
Também construímos a seguinte transformação afim, definida em ![]() :
:
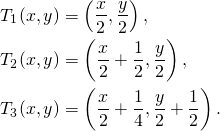
Se ![]() é o tapete de Sierpinski, temos
é o tapete de Sierpinski, temos
![]()
Será que existem outros subconjuntos ![]() do plano que têm a mesma propriedade, a saber :
do plano que têm a mesma propriedade, a saber :
(1) ![]()
Vamos fazer uma experiência e verificar que a resposta é não. Assim, caracterizamos nosso tapete de Sierpinski como sendo o único subconjunto B do plano que satisfaz (1). O que fizemos? Construímos uma função que associa um subconjunto ![]() do plano ao subconjunto
do plano ao subconjunto ![]() . Vamos chamar essa função de
. Vamos chamar essa função de ![]() . Ela é definida por
. Ela é definida por
(2) ![]()
e vimos que ![]() , isto é,
, isto é, ![]() é um ponto fixo dessa função.
é um ponto fixo dessa função.
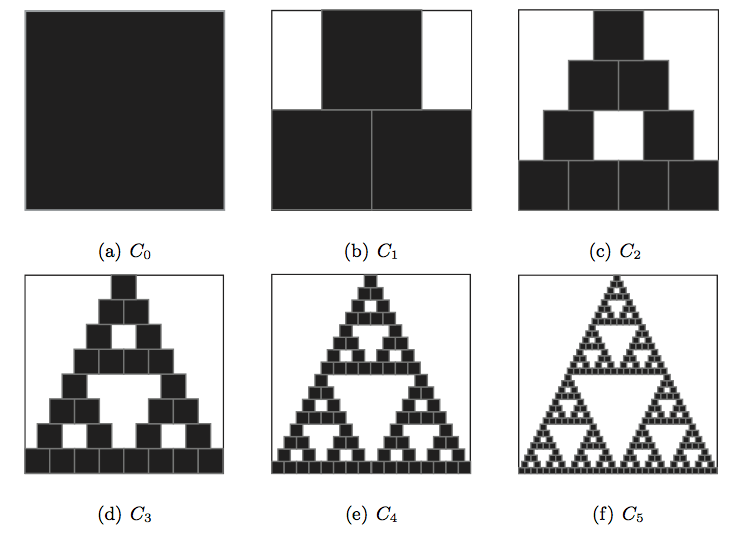
Dissemos que faríamos uma experiência para mostrar que o tapete de Sierpinski é o único ponto fixo dessa função.Tentemos com um quadrado ![]() como na Figura 1(a). Sua imagem é
como na Figura 1(a). Sua imagem é ![]() na Figura 1(b). Aplicamos o mesmo processo a
na Figura 1(b). Aplicamos o mesmo processo a ![]() e obtemos
e obtemos ![]() ,
, ![]() –
–![]() . (Figura 1 (c)-(f)).
. (Figura 1 (c)-(f)).
Observamos três fatos:
- Nenhum dos conjuntos
 , …,
, …,  é um ponto fixo de
é um ponto fixo de 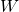 .
.
- Poderíamos ter continuado o processo indefinidamente, produzindo uma sequência infinita de conjuntos
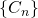 , com
, com 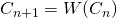 .
.
- A sequência
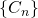 parece convergir rapidamente para o tapete de Sierpinski. De fato, nossos olhos não conseguem distinguir
parece convergir rapidamente para o tapete de Sierpinski. De fato, nossos olhos não conseguem distinguir 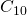 de
de  . Então, no lugar de
. Então, no lugar de  , o programa de reconstrução da nossa imagem pode simplesmente produzir
, o programa de reconstrução da nossa imagem pode simplesmente produzir 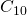 . E, se uma resolução melhor for necessária, usaremos o mesmo programa mandando-o parar em
. E, se uma resolução melhor for necessária, usaremos o mesmo programa mandando-o parar em 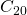 , ou
, ou 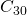 . Assim, o mesmo pequeno programa pode reconstruir
. Assim, o mesmo pequeno programa pode reconstruir  com precisão arbitrária.
com precisão arbitrária.
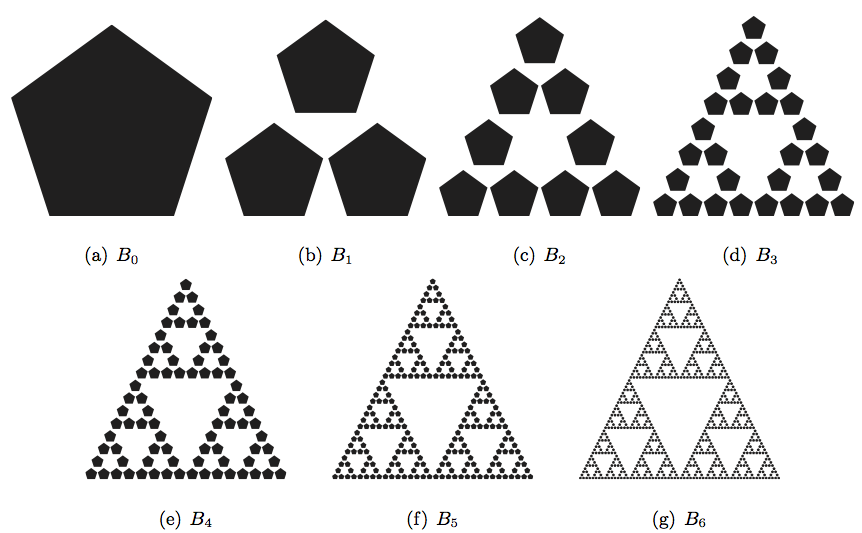
Além disso, pode-se refazer essa experiência e ver que ela funciona com qualquer conjunto de partida. Um segundo exemplo com um pentágono é mostrado na Figura 2. As mesmas observações i, ii e iii acima podem ser aplicadas a esse exemplo.
Vimos que o teorema do ponto fixo de Banach se aplica às contrações em espaços métricos completos. Em (2) definimos a função ![]() para subconjuntos do plano. O espaço métrico
para subconjuntos do plano. O espaço métrico ![]() a ser considerado será o conjunto dos subconjuntos (fechados) limitados do plano. Vamos introduzir uma distância em
a ser considerado será o conjunto dos subconjuntos (fechados) limitados do plano. Vamos introduzir uma distância em ![]() chamada distância de Hausdorff. A definição de distância de Hausdorff,
chamada distância de Hausdorff. A definição de distância de Hausdorff, ![]() , entre dois subconjuntos
, entre dois subconjuntos ![]() e
e ![]() é uma fórmula obscura e complicada; por isso explicaremos essa noção de uma maneira diferente. Começaremos, explicando o significado que é dado à expressão
é uma fórmula obscura e complicada; por isso explicaremos essa noção de uma maneira diferente. Começaremos, explicando o significado que é dado à expressão
![]()
(mesmo que não tenhamos definido o significado de ![]() ). A expressão nos diz que se nossos olhos tiverem uma precisão
). A expressão nos diz que se nossos olhos tiverem uma precisão ![]() , eles não conseguirão distinguir
, eles não conseguirão distinguir ![]() de
de ![]() . Em termos matemáticos,
. Em termos matemáticos, ![]() significa
significa
(3) ![]()
(aqui ![]() é a distância euclidiana usual em
é a distância euclidiana usual em ![]() .) Isso nos permite dar a seguinte definição indireta.
.) Isso nos permite dar a seguinte definição indireta.
Definição. A distância de Hausdorff entre dois conjuntos fechados e limitados ![]() e
e ![]() é o mínimo de todos os
é o mínimo de todos os ![]() tais que a condição (3) é satisfeita.
tais que a condição (3) é satisfeita.
Podemos nos convencer agora que a função ![]() é uma contração. De fato, suponha que
é uma contração. De fato, suponha que ![]() . Então podemos mostrar que
. Então podemos mostrar que ![]() . Seja
. Seja ![]() . Então existe
. Então existe ![]() e
e ![]() tais que
tais que ![]() . Como
. Como ![]() , existe
, existe ![]() tal que
tal que ![]() . sera
. sera ![]() . Então
. Então ![]() e
e ![]() . Analogamente, se começarmos com
. Analogamente, se começarmos com ![]() existe
existe ![]() tal que
tal que ![]() .
.
Esse processo foi adaptado para a compressão de imagens reais (ver [K] ou [RS]. O método produz imagens de ótima qualidade quando a imagem original tem caráter fractal. No entanto o nível de compressão não é tão flexível, nem tão eficiente como o formato JPEG. Também, o processo de codificação (transformando a imagem em um programa para reconstruí-la) é ainda demasiadamente complexo para ter interesse prático. No entanto, a simplicidade da ideia juntamente com sua potência continua sendo impressionante e muito sedutora.
4. Uma aplicação surpreendente: o algoritmo PageRank
O sucesso de Google como instrumento de busca vem do seu algoritmo: o algoritmo PageRank. Nesse algoritmo calcula-se um ponto fixo de um operador linear em ![]() que é uma contração e esse ponto fixo (que é um vetor) produz a ordenação das páginas. Na prática, o ponto fixo (que é um autovetor do autovalor 1) é calculado aproximadamente como
que é uma contração e esse ponto fixo (que é um vetor) produz a ordenação das páginas. Na prática, o ponto fixo (que é um autovetor do autovalor 1) é calculado aproximadamente como ![]() para
para ![]() suficientemente grande. Convidamos o leitor interessado olhar os detalhes no artigo Como Google funciona ?
suficientemente grande. Convidamos o leitor interessado olhar os detalhes no artigo Como Google funciona ?
5. Conclusão
Vimos neste artigo como, a partir de um simples jogo, podemos descobrir ideias muito poderosas que podem levar a maiores avanços na matemática e na tecnologia. Quando procuramos uma solução única de um problema, é normal hoje em dia, em vários domínios da matemática, tentar ver se a solução do problema pode ser caracterizada como sendo o único ponto fixo de um operador especialmente construído para esse fim.
Vimos que a vantagem desse procedimento é que o teorema fornece um método eficiente e concreto de construir a solução como o limite de uma sequência porque a convergência é rápida.
Análise Matemática é o estudo de funções. Funções são geralmente definidas em conjuntos numéricos. Na análise de várias variáveis, generaliza-se a noção de funções para vetores que são elementos de ![]() ? Mas por que parar nos elementos de
? Mas por que parar nos elementos de ![]() ? Vimos também que os matemáticos gostam de generalizar a noção de funções e se permitem defini-las, por exemplo, em conjuntos de conjuntos, em conjuntos de funções, etc. Análise em conjuntos de funções é atualmente um capítulo importante da análise moderna, chamada análise funcional que é standard em estudos de pós graduação.
? Vimos também que os matemáticos gostam de generalizar a noção de funções e se permitem defini-las, por exemplo, em conjuntos de conjuntos, em conjuntos de funções, etc. Análise em conjuntos de funções é atualmente um capítulo importante da análise moderna, chamada análise funcional que é standard em estudos de pós graduação.
Você está convidado a estabelecer um elo com algum processo iterativo que você tenha encontrado. Por exemplo, com os processos iterativos em dimensão 1, associados às sequências de Heron, para obter raízes quadradas. A convergência rápida das sequências geométricas pode igualmente ser compreendida sob o ponto de vista explicado neste artigo.
Bibliografia
[B] M. F. Barnsley, Fractals everywhere, San Diego, Academic Press, 1988.
[K] J. Kominek, Advances in fractal compression for
multimedia applications, Multimedia Systems Journal, vol. 5,
n![]() 4, 1997, 255–270.
4, 1997, 255–270.
[R] C. Rousseau, Point fixe de Banach (in French), Accromath 5, hiver-printemps 2010 (www.accromath.ca).
[R2] C. Rousseau, How Google works? Klein vignette (www.kleinproject.org).
[RS] C. Rousseau and Y. Saint-Aubin, Mathematics and
technology, SUMAT Series, Springer-Verlag, 2008 (A French version of the book, Mathéematiques et technologie, exists, published in the same series.)
Este post está disponível em: Inglês, Francês, Italiano, Espanhol, Árabe, Khmer

 Português
Português 简体中文
简体中文  English
English  Français
Français  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer
please sent information about the applications in the real world of the fixed point theory.my field of interesting is educational matematics .