 Dirce Uesu Pesco e Humberto José Bortolossi.
Dirce Uesu Pesco e Humberto José Bortolossi.
Le immagini che si vedono sulle pagine internet e le foto che si fanno con il cellulare sono esempi di immagini digitali. É possibile rappresentare questo tipo di immagine usando le matrici. Per esempio, la piccola immagine di Felix il Gatto (sulla sinistra) può essere rappresentata da una matrice ![]() i cui elementi sono i numeri
i cui elementi sono i numeri ![]() e
e ![]() . Questi numeri specificano il colore di ciascun pixel (un pixel è il più piccolo elemento grafico di un immagine matriciale, che può assumere solo un colore per volta): il numero
. Questi numeri specificano il colore di ciascun pixel (un pixel è il più piccolo elemento grafico di un immagine matriciale, che può assumere solo un colore per volta): il numero ![]() indica il nero e il numero
indica il nero e il numero ![]() indica il bianco. Le immagini digitali che usano solo due colori sono chiamate immagini binarie o booleane.
indica il bianco. Le immagini digitali che usano solo due colori sono chiamate immagini binarie o booleane.
Anche le immagini in scala di grigi possono essere rappresentate da matrici. Ogni elemento della matrice determina l’intensità del pixel corrispondente. Per convenienza, la maggior parte degli attuali file digitali usano numeri interi compresi tra ![]() (per indicare il nero, il colore con intensità minima) e
(per indicare il nero, il colore con intensità minima) e ![]() (per indicare il bianco, il colore con la massima intensità), per un totale di
(per indicare il bianco, il colore con la massima intensità), per un totale di ![]() diverse gradazioni di grigio (Un tale numero di gradazioni è ragionevole per lavorare con le immagini delle pagine WEB. Tuttavia, esistono alcune applicazioni specifiche che hanno bisogno di più gradazioni di grigio per riprodurre l’immagine più dettagliata ed evitare gli errori di arrotondamento nei calcoli numerici, come nel caso delle immagini ad uso medico).
diverse gradazioni di grigio (Un tale numero di gradazioni è ragionevole per lavorare con le immagini delle pagine WEB. Tuttavia, esistono alcune applicazioni specifiche che hanno bisogno di più gradazioni di grigio per riprodurre l’immagine più dettagliata ed evitare gli errori di arrotondamento nei calcoli numerici, come nel caso delle immagini ad uso medico).
Le immagini a colori, a loro volta, possono essere rappresentate da tre matrici. Ogni matrici specifica la quantità di rosso, verde e blu che compone l’immagine. Questo sistema di colori è noto come RGB (Esistono molti altri sistemi di colori che vengono usati a seconda dell’applicazione in questione: CMYK (per stampare), Y’IQ (per la trasmissione analogica TV in NTSC), ecc). Gli elementi di queste matrici sono numeri interi compresi tra ![]() e
e ![]() e determinano l’intensità del pixel relativamente al colore della matrice. Quindi, nel sistema RGB, è possibile rappresentare
e determinano l’intensità del pixel relativamente al colore della matrice. Quindi, nel sistema RGB, è possibile rappresentare ![]() colori diversi.
colori diversi.
Trattamento di un’immagine digitale e operazioni con le matrici
Una volta che un’immagine digitale può essere rappresentata con delle matrici, possiamo chiederci come le operazioni sui loro elementi influenzino l’immagine corrispondente. Per esempio, se consideriamo l’immagine binaria ![]() in Figura 3 come una matrice, sia
in Figura 3 come una matrice, sia ![]() allora l’immagine corrisponde l’immagine
allora l’immagine corrisponde l’immagine ![]() corrisponde alla matrice trasposta di
corrisponde alla matrice trasposta di ![]() , ossia
, ossia ![]() . L’immagine
. L’immagine ![]() , a sua volta, corrisponde alla matrice
, a sua volta, corrisponde alla matrice ![]() . Prova a scoprire le relazioni matriciali tra l’immagine
. Prova a scoprire le relazioni matriciali tra l’immagine ![]() e le altre immagini!
e le altre immagini!
Un altro esempio: se consideriamo la media aritmetica standard delle matrici ![]() ,
, ![]() e
e ![]() che compongono un’immagine a colori
che compongono un’immagine a colori ![]() , otterremo una versione in scala di grigi dell’immagine (i valori non-interi vengono arrotondati all’intero più vicino):
, otterremo una versione in scala di grigi dell’immagine (i valori non-interi vengono arrotondati all’intero più vicino):
Un ulteriore esempio: usando le operazioni di moltiplicazione per uno scalare e della somma di matrici, è possibile creare un’effetto di transizione comunemente usato, per esempio, nelle presentazioni PowerPoint![]() e di slide. Più precisamente, consideriamo due immagini in scala di grigi della stessa grandezza, rappresentate dalla matrici
e di slide. Più precisamente, consideriamo due immagini in scala di grigi della stessa grandezza, rappresentate dalla matrici ![]() e
e ![]() . Per ogni scalare (numero reale)
. Per ogni scalare (numero reale) ![]() nell’intervallo
nell’intervallo ![]() , si definisca la matrice
, si definisca la matrice
![]()
Si osservi che ![]() ,
, ![]() e per ogni
e per ogni ![]() compreso tra
compreso tra ![]() e
e ![]() , gli elementi della matrice
, gli elementi della matrice ![]() sono compresi tra gli elementi delle matrici
sono compresi tra gli elementi delle matrici ![]() e
e ![]() . Perciò, quando
. Perciò, quando ![]() varia da
varia da ![]() a
a ![]() , la matriceare
, la matriceare ![]() varia da
varia da ![]() a
a ![]() . Nel caso di un’immagine a colori, la trasformazione (1) deve essere applicata alle matrici
. Nel caso di un’immagine a colori, la trasformazione (1) deve essere applicata alle matrici ![]() ,
, ![]() e
e ![]() che determinano ogni immagine.
che determinano ogni immagine.
Anche la moltiplicazione di matrici ha applicazioni nel trattamento di un’immagine digitale. Sebbene il nostro prossimo esempio sarà più elaborato, (con un ragionamento basato su tecniche matematiche più avanzate solitamente studiate solo ai corsi universitari di Algebra Lineare), crediamo che possa essere comunque interessante per il lettore, poiché quest’ultimo avrà l’opportunità di apprezzare una sorprendente applicazione dovuta al fatto che siamo in grado di scomporre una matrice come prodotto di matrici aventi strutture speciali. I dettagli omessi potranno essere trovati nei riferimenti bibliografici [Lay, 2011] e [Poole, 2005]. Si consideri, dunque, una scomposizione a valori singolari (SVD), che consiste in scrivere una matrice come il prodotto di tre
matrici:
![]()
Qui di seguito è riportato un esempio della decomposizione SVD:
![]()
![Rendered by QuickLaTeX.com \[= \left[ \begin{array}{rr} \displaystyle -\frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{2}}{2} \vspace*{0.5ex} \\ \displaystyle \frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{2}}{2} \end{array} \right] \left[ \begin{array}{rrr} \sqrt{3} & 0 & 0 \\ 0 & 1 & 0 \end{array} \right] \left[ \begin{array}{rrr} \displaystyle \frac{\sqrt{6}}{6} & \displaystyle -\frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{3}}{3} \vspace*{0.5ex} \\ \displaystyle -\frac{\sqrt{6}}{3} & 0 & \displaystyle \frac{\sqrt{3}}{3} \vspace*{0.5ex} \\ \displaystyle \frac{\sqrt{6}}{6} & \displaystyle \frac{\sqrt{2}}{2} & \displaystyle \frac{\sqrt{3}}{3} \end{array} \right]^{T}. $ } }\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-ea1423e6087d57b5cf5ae935b0aa069e_l3.png)
Può essere dimostrato che ogni matrice ammette una decomposizione SVD ([Lay, 2011],[Poole, 2005]). In più, esistono algoritmi che ci permettono di calcolare questo tipo di decomposizioni usando un computer. Il punto chiave del nostro esempio è osservare che se ![]() sono le colonne della matrice
sono le colonne della matrice ![]() e
e ![]() sono le colonne della matrice
sono le colonne della matrice ![]() , allora
, allora
![]()
Perché questo? Supponiamo che ![]() , un’ immagine in scala di grigio di dimensioni
, un’ immagine in scala di grigio di dimensioni ![]() , debba essere trasmessa da un satellite a un laboratorio sulla Terra. In linea di principio, il satellite dovrebbe mandare 1 milione di numeri (uno per ciascun pixel). Tipicamente, poiché, sono significativi solo i primi
, debba essere trasmessa da un satellite a un laboratorio sulla Terra. In linea di principio, il satellite dovrebbe mandare 1 milione di numeri (uno per ciascun pixel). Tipicamente, poiché, sono significativi solo i primi ![]() elementi della matrice
elementi della matrice ![]() della decomposizione SVD per
della decomposizione SVD per ![]() (gli altri sono “piccoli”), è, quindi, sufficiente che il satellite mandi, diciamo, le prime
(gli altri sono “piccoli”), è, quindi, sufficiente che il satellite mandi, diciamo, le prime ![]() colonne di
colonne di ![]() e di
e di ![]() e i primi
e i primi ![]() numeri
numeri ![]() (per un totale di soli
(per un totale di soli ![]() numeri che devono essere inviati). Alla ricezione di questi dati, il laboratorio sulla Terra calcola la matrice
numeri che devono essere inviati). Alla ricezione di questi dati, il laboratorio sulla Terra calcola la matrice ![]() che darà un’approssimazione dell’immagine originaria.
che darà un’approssimazione dell’immagine originaria.
Vediamo un esempio: la Figura 6 del matematico Christian Felix Klein (1849-1925) ha ![]() pixel.
pixel.
Dalla decomposizione SVD della matrice corrispondente di questa immagine, possiamo calcolare le matrici ![]() per
per ![]() e
e ![]() . Queste matrici generano approssimazioni dell’immagine originaria, come illustrato nella Figura 7. Notiamo che l’immagine originaria corrisponde al caso
. Queste matrici generano approssimazioni dell’immagine originaria, come illustrato nella Figura 7. Notiamo che l’immagine originaria corrisponde al caso ![]() . È piuttosto notevole, non credete?
. È piuttosto notevole, non credete?
Altre applicazioni
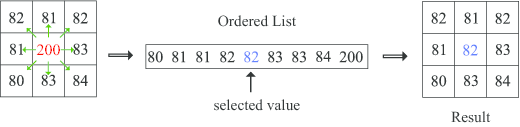
L’elaborazione delle immagini digitali ha molte applicazioni, come il telerilevamento, la trasmissione di dati, la medicina, la robotica, la computer vision, l’industria dei film, ecc. Nel telerilevamento, per esempio, le immagini acquisite dai satelliti sono utili per il monitoraggio di risorse naturali, per la mappatura geografica, per l’analisi della crescita urbana e per molte altre applicazioni ambientali. Nella trasmissione delle immagini, abbiamo comunicazioni via fax, reti, internet e TV a circuito chiuso per il monitoraggio e la sicurezza. Nelle applicazioni mediche, abbiamo elaborazione delle immagini ai raggi X, immagini di proiezione di tomografie transassiali, la radiologia, la risonanza magnetica nucleare (RNM) e la scansione a ultrasuoni. Alcuni metodi di acquisizione e di trasmissione possono generare imperfezioni in un’immagine. Il filtro mediano è una tecnica dell’elaborazione dell’ immagine usata per rimuoverle o per ridurre i loro effetti: per ogni elemento della matrice che rappresenta l’immagine, osserviamo i suoi elementi periferici e, poi, li disponiamo in un vettore ordinato. Il filtro mediano consiste nello scegliere l’elemento centrale di questo vettore e nel sostituire con esso l’elemento centrale della matrice (Figura 8).
Nell’elaborazione di immagini, esistono molte altre tecniche con obiettivi diversi. Le immagini in Figura 10 illustrano esempi di aggiustamento di contrasto, di rilevamento e di soglia del bordo.
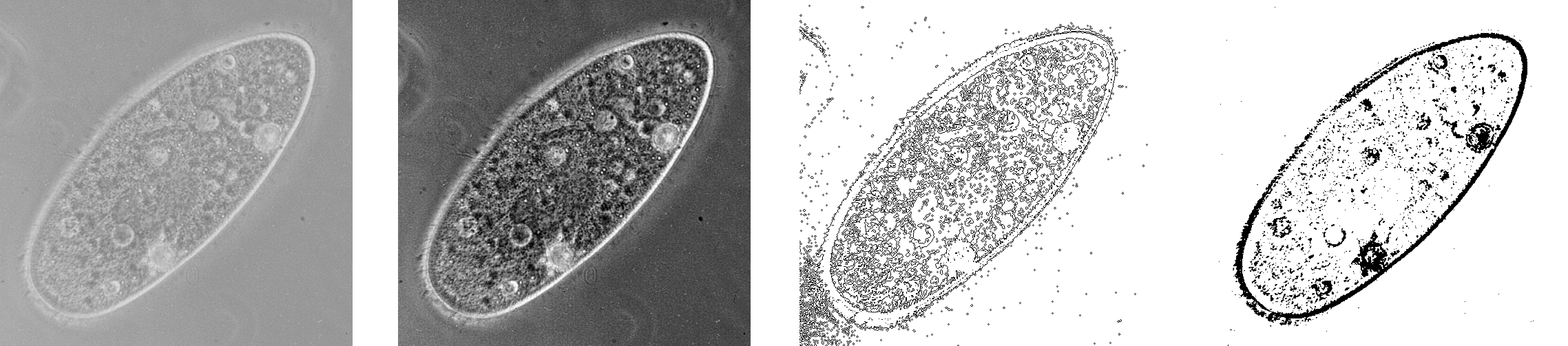
Figura 10: immagine originaria e la stessa immagine con l’aggiustamento di contrasto, con il rilevamento del bordo e con il valore di soglia
Commento finale
Il nostro obiettivo, con questo articolo, è di presentare agli insegnanti e agli studenti della scuola media superiore un’ applicazione delle matrici poco conosciuta: l’elaborazione delle immagini digitali. È importante notare che gli strumenti matematici collegati a questo argomento vanno ben al di là delle matrici. Il soggetto è vasto, ricco e moderno. Sfortunatamente, il limite di poche pagine a disposizione per questo articolo non ci permette di fornire ulteriori dettagli. Come punto di partenza per il lettore motivato a saperne di più, raccomandiamo i libri [Gonzalez e Woods, 2007] e [Gomes e Velho, 2008].
Su questo sito web (or at its mirror)), è presente una serie di applet interattive che permettono di esplorare le relazioni tra le matrici e le immagini digitali presentate in questo testo. Potrete trovare, inoltre, un file DOC con suggerimenti di esercizi da proporre in classe.
Qui sotto sono presenti i riferimenti citati nel testo.
Riferimenti bibliografici
Gomes, J.; Velho, L. Image Processing for Computer Graphics and Vision. Springer-Verlag, 2008.
Gonzalez, R. C.; Woods, R. E. Digital Image Processing. Third Edition. Prentice Hall, 2007.
Lay, D. Linear Algebra and Its Applications. Forth Edition. Addison Wesley, 2011.
Poole, D. Linear Algebra: A Modern Introduction. Second Edition. Brooks Cole, 2005.
The photo of the Mona Liza in LEGO is a property of Marco Pece Udronotto, who kindly granted permission to use it in this work.









Voici une traduction.
L’exemple est sympa en effet pour des étudiants.
——-
“Matrices et images numériques”
Les images qu’on voit sur les pages web et les photos qu’on prend avec le téléphone portable sont des exemples d’images numériques.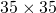 dont les éléments sont les nombres 0 et 1.
dont les éléments sont les nombres 0 et 1.
Il est possible de représenter ce type d’image en utilisant des matrices. Par exemple, la petite image de Felix le Cat (à gauche) peut être représentée par une matrice
Ces nombres indiquent la couleur de chaque pixel (un pixel est le plus petit élément graphique d’une image matricielle, ce qui peut prendre une seule couleur à la fois): le nombre 0 indique le noir et le 1 indique le blanche. Les images numériques qui utilisent seulement deux couleurs sont appelées “images binaires” ou “booléennes”.
——
Sorry, I don’t see any imagine