Von David Mumford and Christiane Rousseau
Aus dem Englischen übersetzt von Anna Muff (Universität Würzburg)
Vorwort: Dieser Klein-Artikel ist anspruchsvoller als andere. Dennoch beschreibt er auf wenigen Seiten wie eines der schwierigsten offenen Probleme des Anfangs des 21. Jahrhunderts mit einfachen Worten erklärt werden kann. Der Klein-Artikel enthält bereicherndes Material, das zum Lesen gewählt werden oder übersprungen werden kann. Die Herausgeber des Klein-Blogs zögerten eine Weile, bevor sie diesen Artikel posteten. Nachdem er aber mit Lehrern in zwei Klein-Workshops getestet wurde, die danach sagten, dass sie gerne die Herausforderung von schwierigeren Klein-Artikeln annehmen, wurde beschlossen sie auf dem Blog zu testen. Die Herausgeber sind gespannt auf Kommentare und darauf, ob jemand von dem Thema motiviert wurde.
Sie haben wahrscheinlich schon davon gehört, dass einige Flugzeuge die Schallmauer durchbrochen haben. Was bedeutet das? Es bedeutet, dass eine Stoßwelle in der Atmosphäre verursacht wurde, wie in Abbildung 1. Aber was ist eine Stoßwelle? Stellen Sie sich dichten Verkehr auf Autobahnen als Welle vor. Eine Stoßwelle entspricht einem Zusammenstoß. Um das zu erklären beschreiben wir unsere erste Intuition mit einem 1D-Modell: Verkehr auf einer einspurigen Straße mit unterschiedlichen Geschwindigkeiten. Wie Sie wissen, können Auffahrunfälle durch nicht angepasste Geschwindigkeit entstehen. Die Atmosphäre ist ein Fluid und Verkehr ist ein großes Modell eines eindimensionalen Fluides, das sich eignet, um unsere erste Eingebung weiterzuentwickeln. Unter welchen Bedingungen entstehen Stoßwellen oder andere Besonderheiten in Fluiden? Ein Preis von einer Million Dollar ist auf die Antwort dieser Frage ausgesetzt. Das ist das, was wir Ihnen erklären möchten.
1. 1D-Modelle
Die Burgersgleichung
Konstruieren wir ein einfaches Verkehrsmodell. Wir betrachten Autos an jeder Stelle entlang einer Geraden, die eine Straße darstellt. Zum Zeitpunkt ![]() hat das Auto an der Stelle
hat das Auto an der Stelle ![]() die Geschwindigkeit
die Geschwindigkeit ![]() . Das Auto, das bei
. Das Auto, das bei ![]() startet, wird zum Zeitpunkt
startet, wird zum Zeitpunkt ![]() an der Stelle
an der Stelle ![]() sein. Sei nun
sein. Sei nun ![]() die Geschwindigkeit des Autos an der Stelle zum Zeitpunkt . Die Annahme ist nun, dass Autos mit konstanter Geschwindigkeit auf einer geraden Straße fahren. Also haben wir
die Geschwindigkeit des Autos an der Stelle zum Zeitpunkt . Die Annahme ist nun, dass Autos mit konstanter Geschwindigkeit auf einer geraden Straße fahren. Also haben wir ![]() , diese Funktion ist also konstant . Daraus folgt, dass ihre Ableitung Null ist. Nach der Kettenregel für Ableitungen von mehreren Variablen ergibt sich
, diese Funktion ist also konstant . Daraus folgt, dass ihre Ableitung Null ist. Nach der Kettenregel für Ableitungen von mehreren Variablen ergibt sich
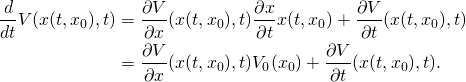
Wenn nun ![]() die Stelle auf der Straße mit
die Stelle auf der Straße mit ![]() ist, wird die Verkehrsgleichung zur sogenannten Burgersgleichung:
ist, wird die Verkehrsgleichung zur sogenannten Burgersgleichung:
(1) ![]()
Diese Gleichung besagt, dass jedes Auto eine konstante Geschwindigkeit beibehält, während es auf der Straße entlangfährt.
Oder anders ausgedrückt: Wenn ein Auto an der Stelle ![]() mit der Geschwindigkeit
mit der Geschwindigkeit ![]() losfährt, dann wird es zum Zeitpunkt
losfährt, dann wird es zum Zeitpunkt ![]() an der Stelle
an der Stelle ![]() immer noch dieselbe Geschwindigkeit haben:
immer noch dieselbe Geschwindigkeit haben: ![]() für jedes
für jedes ![]() .
.
Das ist natürlich kein praktikables Verhalten! Es werden Unfälle passieren. Abbildung 2 zeigt ein so entstandenes Chaos.

Abb. 2: Eine Druckwelle in der Burgersgleichung für die Anfangsgeschwindigkeit V(x)=exp(-x^2). Dargestellt sind die Weltlinien von Autos, die zu Beginn jeweils den gleichen Abstand auf der Straße haben. Die dicke schwarze Linie steht für die Unfälle, die passieren.
Beschreibung der Stöße
Was passiert, wenn wir uns dem Zusammenstoß nähern? Angenommen am Anfang (![]() ) hatten zwei Punkte
) hatten zwei Punkte ![]() <
<![]() die Geschwindigkeiten
die Geschwindigkeiten ![]() . Die Stelle
. Die Stelle ![]() zum Zeitpunkt
zum Zeitpunkt ![]() wird nun
wird nun ![]() genannt. Ebenso bezeichnet
genannt. Ebenso bezeichnet ![]() die Position von
die Position von ![]() zum Zeitpunkt
zum Zeitpunkt ![]() mit
mit ![]() . Dann nähert sich
. Dann nähert sich ![]() immer mehr an
immer mehr an ![]() an, kurz vor dem Stoß ist sehr nah bei
an, kurz vor dem Stoß ist sehr nah bei ![]() . Trotzdem bleibt die Differenz ihrer Geschwindigkeiten
. Trotzdem bleibt die Differenz ihrer Geschwindigkeiten ![]() dieselbe.
dieselbe.
Das bedeutet, dass die mittlere Steigung der Funktion ![]() als Funktion in Abhängigkeit von
als Funktion in Abhängigkeit von ![]() für ein festes
für ein festes ![]() sehr groß wird (siehe dazu Abbildung 3, die den Graphen
sehr groß wird (siehe dazu Abbildung 3, die den Graphen ![]() als Funktion in Abhängigkeit von
als Funktion in Abhängigkeit von ![]() für mehrere Werte von
für mehrere Werte von ![]() zeigt). Demzufolge sehen wir, dass
zeigt). Demzufolge sehen wir, dass ![]() bei Annäherung an den Stoß unendlich wird. Das bedeutet, dass die Differentialgleichung (1) bei dem Stoß eine Definitionslücke hat.
bei Annäherung an den Stoß unendlich wird. Das bedeutet, dass die Differentialgleichung (1) bei dem Stoß eine Definitionslücke hat.
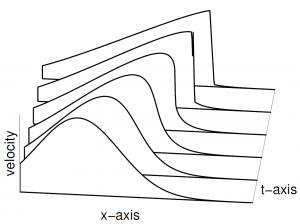
Abb. 3: Auf die gleiche Weise wie in Abbildung 2 ist hier der Graph der Geschwindigkeit als Raumfunktion zu sechs Zeitpunkten dargestellt. Bemerkenswert ist, wie die Geschwindigkeit unstetig wird, wenn sich die Stoßwelle bildet. Die Steigung der Geschwindigkeit wird für feste x, ebenso wie für feste t, unendlich.
2. Richtige Stöße modellieren oder modellieren, wie sie vermieden werden können?
Wir haben eine Situation modelliert, in der alle Autos, die die Straße entlangfahren, niemals ihre Geschwindigkeit ändern. Wenn die Funktion mit ![]() steigt, dann sind alle vorderen Autos schneller als die hinteren und es entsteht kein Problem. Wenn nun aber einige langsamere Autos vor den schnelleren fahren, wird es zu einer Kollision kommen, wenn niemand seine Geschwindigkeit anpasst. Das Modell kann auf zwei Arten weiterentwickelt werden. Um auf die eigentliche Motivation, die Überschallstoßwelle, zurückzukommen, können wir unsere Gleichung so verfeinern, dass sie Kollisionen, eindimensionale Versionen von Stößen, einschließt. Die zugrundeliegende Ursache ist dieselbe wie bei Überschallflugzeugen, die Luft vor dem Flugzeug kann sich nämlich nicht schnell genug fortbewegen, um dem sich nähernden Flugzeug auszuweichen! Oder wir können unsere Gleichung so weiterentwickeln, dass sie eine intelligentere Fahrweise zulässt, so dass das schnellere Auto abbremsen und das langsamere Auto beschleunigen kann.
steigt, dann sind alle vorderen Autos schneller als die hinteren und es entsteht kein Problem. Wenn nun aber einige langsamere Autos vor den schnelleren fahren, wird es zu einer Kollision kommen, wenn niemand seine Geschwindigkeit anpasst. Das Modell kann auf zwei Arten weiterentwickelt werden. Um auf die eigentliche Motivation, die Überschallstoßwelle, zurückzukommen, können wir unsere Gleichung so verfeinern, dass sie Kollisionen, eindimensionale Versionen von Stößen, einschließt. Die zugrundeliegende Ursache ist dieselbe wie bei Überschallflugzeugen, die Luft vor dem Flugzeug kann sich nämlich nicht schnell genug fortbewegen, um dem sich nähernden Flugzeug auszuweichen! Oder wir können unsere Gleichung so weiterentwickeln, dass sie eine intelligentere Fahrweise zulässt, so dass das schnellere Auto abbremsen und das langsamere Auto beschleunigen kann.
Klügere Fahrer
Wenn ein Zusammenstoß droht, würde das Verhalten eines intelligenten Fahrers sicherlich von seinen Nachbarn beeinflusst werden, indem er wohl seine Geschwindigkeit der seiner Nachbarn anpassen wird. Die Analogie ist, an eine zähflüssige Masse zu denken: Wer schon einmal fließenden Honig beobachtet hat, wird bemerkt haben, dass er sich als Ganzes verhält, als ob alle Teile zusammenhängen würden. Keine Tropfen spritzen herum, alle sind mit dem Hauptfluss verbunden. Die Viskosität von Wasser ist etwa 10 000 Mal geringer, die von Luft etwa 50 Mal – aber sie ist nicht gleich null. Eine mögliche Korrektur der Burgersgleichung, die Zusammenstöße vermeidet, wenn die Anfangsgeschwindigkeit ![]() abhängig ist, schließt das Hinzunehmen eines Viskositätsterms ein. Solch ein Term ist einfach ein Vielfaches der zweiten Ableitung
abhängig ist, schließt das Hinzunehmen eines Viskositätsterms ein. Solch ein Term ist einfach ein Vielfaches der zweiten Ableitung ![]() . Daher nimmt die veränderte Gleichung, die auch als viskose Burgersgleichung bekannt ist, folgende Form an:
. Daher nimmt die veränderte Gleichung, die auch als viskose Burgersgleichung bekannt ist, folgende Form an:
(2) ![]()
Wobei ![]() Viskosität genannt wird. Die veränderten Weltlinien sind in Abbildung 4 dargestellt, für dieselbe Funktion
Viskosität genannt wird. Die veränderten Weltlinien sind in Abbildung 4 dargestellt, für dieselbe Funktion ![]() , die die Anfangsgeschwindigkeit, wie in Abbildung 2, beschreibt.
, die die Anfangsgeschwindigkeit, wie in Abbildung 2, beschreibt.
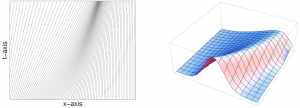
Abb. 4: In derselben Situation wie in Abb. 2 nehmen wir Viskosität hinzu und stellen fest, dass die Autos näher zusammenrücken, aber nicht mehr kollidieren. Auf der rechten Seite ist der Graph von V(x,t) abgebildet.
Welche Bedeutung hat hier eine zweite Ableitung? Rufen wir uns diese zweite Ableitung als Grenzwert von
(3) ![]()
ins Gedächtnis.
Dies kann man daran sehen, dass das die erste Ableitung der ersten Ableitung ist, also etwa
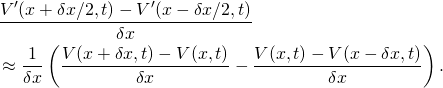
Dieser Ausdruck kann umgeschrieben werden zu
![]()
Was bedeutet der zweite Faktor? Es ist der Mittelwert von zwei Funktionen: der erste ist die Differenz der Geschwindigkeit vorne und in der Mitte, und der zweite ist die Differenz der Geschwindigkeit hinten und in der Mitte. Die Gefahr einer Kollision besteht, wenn ![]() . In diesem Fall ist der erste Term negativ und der zweite positiv. Wenn der erste Term gewinnt, ist der Mittelwert negativ und Ausdruck (3) gibt an, dass gebremst werden soll, da die linke Seite die Beschleunigung ist. Kurz bevor es zu einer Kollision kommt, wird es eine Unstetigkeit in der Geschwindigkeit geben, wobei ein schnelleres Auto kurz davor ist ein langsameres zu erreichen.
. In diesem Fall ist der erste Term negativ und der zweite positiv. Wenn der erste Term gewinnt, ist der Mittelwert negativ und Ausdruck (3) gibt an, dass gebremst werden soll, da die linke Seite die Beschleunigung ist. Kurz bevor es zu einer Kollision kommt, wird es eine Unstetigkeit in der Geschwindigkeit geben, wobei ein schnelleres Auto kurz davor ist ein langsameres zu erreichen.
Durch Hinzunehmen der Viskosität werden die Stöße aus der Burgersgleichung entfernt. Nun können wir dazu übergehen etwas über den Preis von einer Million Dollar zu sagen. Für feste ![]() repräsentiert die linke Seite die Beschleunigung, da sie die Ableitung der Funktion
repräsentiert die linke Seite die Beschleunigung, da sie die Ableitung der Funktion ![]() nach
nach ![]() ist. Die abgeänderte viskose Burgersgleichung besagt, dass das mittlere Auto dann beschleunigt, wenn es langsamer ist als die Durchschnittsgeschwindigkeit seiner Nachbarn davor und dahinter. Wenn es schneller ist bremst es ab.
ist. Die abgeänderte viskose Burgersgleichung besagt, dass das mittlere Auto dann beschleunigt, wenn es langsamer ist als die Durchschnittsgeschwindigkeit seiner Nachbarn davor und dahinter. Wenn es schneller ist bremst es ab.
3. Die Herausforderung reale Ströme zu modellieren
Die Modellierung realer Ströme
Wir haben bisher ein wenig geschummelt, um eine schöne, saubere Mathematik aus einer definitiv chaotischeren echten Welt zu machen. Genauer gesagt haben wir die Dichte der Autos auf der Straße vernachlässigt. Bessere Verkehrsmodelle, wie das Lighthill-Whitham-Richards-Modell, beschäftigen sich mit der lokalen mittleren Dichte ![]() , sowie mit einer lokalen mittleren Geschwindigkeit
, sowie mit einer lokalen mittleren Geschwindigkeit ![]() . Dennoch bestimmen verschiedene Versionen der Burgersgleichung diese präzisierten Modelle, weswegen diese Diskussion hier im Grunde trotzdem richtig war.
. Dennoch bestimmen verschiedene Versionen der Burgersgleichung diese präzisierten Modelle, weswegen diese Diskussion hier im Grunde trotzdem richtig war.
Die Bewegung von Luft um ein Flugzeug, vor allem um die Flügel, sowie die Bewegung von Wasser um ein Boot sind Anwendungen in der realen Welt, die von viel größerem Interesse sind. Mathematiker arbeiten an der Modellierung des letztgenannten seit Euler im 18. Jahrhundert. Wasser und Luft sind grundsätzlich verschieden, da Wasser kaum komprimierbar ist, Luft dagegen in hohem Maße. Die Inkompressibilität von Öl beispielsweise wird benutzt, um enorme Kräfte in Maschinen wie Bulldozern und Baggern zu übertragen. Der Preis von einer Million Dollar betrifft den Fall der Inkompressibilität im Dreidimensionalen.
Die Millennium-Probleme
Um die Mathematik im neuen Jahrtausend zu feiern entwarf Landon T. Clay sieben Millennium-Preise. Die Preise wurden ausgeschrieben, um einige der schwierigsten Probleme, mit denen sich Mathematiker um die Jahrtausendwende beschäftigten, zu beschreiben, sowie das Bewusstsein der Öffentlichkeit darauf zu lenken, dass es in der Mathematik noch viele ungelöste Probleme gibt. Ein Preis von jeweils einer Million Dollar ist auf die Lösung eines jeden Problems ausgesetzt – eines davon (die Poincaré-Vermutung) wurde bisher gelöst!
Das Millennium-Problem, das uns interessiert, befasst sich mit Gleichungen, die den Fluss von inkompressiblen Flüssigkeiten mit Viskosität im dreidimensionalen Raum beschreiben: Diese Gleichungen werden Navier-Stokes-Gleichungen genannt, benannt nach Claude-Louis Navier (1785-1836) und George Gabriel Stokes (1819-1903), die an der Bewegung von Fluiden arbeiteten. Abgesehen von der Inkompressibilität, die noch erklärt wird, entsprechen sie gerade der dreidimensionalen Version der Burgersgleichung mit Viskosität.
Was ist daran neu? Die meisten Mathematiker vermuten, dass die Navier-Stokes-Gleichungen keine Stöße oder andere Definitionslücken, wie Wirbel in allen Größen, von groß bis verschwindend klein, beschreiben. Daher sollten die Gleichungen für jede fortschreitende Zeit lösbar sein. Wer das beweist, dem gehört der Preis! In der Wissenschaft ist man sich einer Schlussfolgerung aber erst dann sicher, wenn sie bewiesen ist. Somit gewinnt auch derjenige den Scheck, der ein Beispiel von Anfangsbedingungen vorweist, die einen Stoß oder eine andere Definitionslücken in endlicher Zeit erzeugen. Warum glauben Mathematiker, dass sich kein Stoß oder eine andere Definitionslücken in einer Navier-Stokes-Gleichung entwickeln wird? Das wurde vor Jahrzehnten für zweidimensionale Flüsse von der Russin Olga Ladyzhenskaya bewiesen. Seitdem haben numerische Simulationen angedeutet, dass sich auch im Dreidimensionalen keine Definitionslücken bilden. Die Simulation von partiellen Differentialgleichungen wie diesen ist eine große rechnerische Herausforderung, die anspruchsvolle Algorithmen und Programme, die über einen langen Zeitraum hinweg auf leistungsstarken Rechnern laufen, voraussetzt.
Steht das im Widerspruch zu Abbildung 1? Nein! Luft ist komprimierbar und das Millennium-Problem betrifft inkompressible Fluide.
Der Rest dieses Klein-Artikels stellt in zweierlei Hinsicht eine Bereicherung dar. Zunächst erklären wir, wie wir Lösungen von Burgersgleichungen erlauben, die an bestimmten Stellen keine eindeutige Lösung haben. (siehe Abschnitt 5. Zusatzmaterial 1) Wer sich noch an die Vorlesung zur Analysis in mehreren Variablen erinnert, kann nachlesen, wie die Burgersgeichung abgeändert wird, um die Bewegung von inkompressiblen Fluiden im dreidimensionalen Raum modelliert wird. (siehe Abschnitt 6. Zusatzmaterial 2)
4. Fazit
Was haben wir gelernt? Man hätte sich beispielsweise vorstellen können, dass es so kompliziert ist ein Fluid zu modellieren. Nun ist klar, dass man dafür nur die simplen Prinzipien der Mechanik braucht, die man in der Schule gelernt hat, als Kräfte, Newtongesetze und Energieerhaltung durchgenommen wurden. Außerdem erfordern die Hilfsmittel, die man benötigt, um diese physikalischen Gesetze darzustellen, lediglich die Begriffe, die in einer Vorlesung zur Analysis in mehreren Variablen eingeführt werden. Die Form der Gleichungen, die die Bewegung von Fluiden beschreiben, ist sehr einfach. Zur Lösung dieser Gleichung sind jedoch noch viele Fragen offen, obwohl auf diesem Gebiet schon seit über 200 Jahren auf numerischem und theoretischem Gebiet intensiv geforscht wird.
Wer sich mit der Modellierung von Stößen beschäftigt, hat eine wichtige Facette der Arbeit von Mathematikern kennengelernt. Wenn zu einem Problem keine Lösung existiert, so können Mathematiker evtl. Objekte erschaffen, mit denen eine Lösung gefunden oder dargestellt werden kann. Beispiele sind die Entstehung der komplexen Zahlen, oder die Erweiterung von ![]() mit Wurzeln jeglicher Polynome mit reellen Koeffizienten. So fanden Mathematiker Distributionen für schwache Lösungen von partiellen Differentialgleichungen.
mit Wurzeln jeglicher Polynome mit reellen Koeffizienten. So fanden Mathematiker Distributionen für schwache Lösungen von partiellen Differentialgleichungen.
Das reicht aber nicht für das oben beschriebene Millennium-Problem. Charles L. Fefferman beschreibt das Problem auf der Clay-Website wie folgt: „.., unser Verständnis ist auf einem sehr primitiven Niveau. Standardmethoden aus der Partiellen Differentialrechnung scheinen unangemessen, um das Problem zu lösen. Stattdessen brauchen wir wahrscheinlich ein paar neue, tiefergehende Ideen.“ Vielleicht wird einer unserer Studenten ja eines Tages den Durchbruch schaffen…
5. Zusatzmaterial 1 – Zurück zur Burgersgleichung
Erlauben von singulären Lösungen
Aber Stöße existieren wirklich! Als Wissenschaftler können wir unsere Untersuchungen hier nicht einfach abbrechen. Eine „Definitionslücke“ ist ein großes Problem und einem Mathematiker bleibt gar nichts anderes übrig als seine mathematische Brille aufzusetzen und sich mehr Gedanken über das Verhalten im Zusammenhang mit der Gleichung zu machen. Diese Herangehensweise wird Einführung von allgemeinen oder ‚schwachen‘ Gleichungen, die nicht glatt sind, genannt. In unserem Fall Autos, die mit bestimmten Geschwindigkeiten kollidieren. Das kann man sich als Massenkarambolage vorstellen, bei der immer mehr Autos von links heranrasen, wobei sich der Stau so entwickelt, um mit immer mehr Autos rechts zu kollidieren. Dadurch erlauben wir ![]() unstetig in
unstetig in ![]() zu sein, indem sie links und rechtseinen Grenzwert haben.
zu sein, indem sie links und rechtseinen Grenzwert haben.
Die Gleichung benutzt aber Ableitungen von ![]() . Um damit umzugehen, benötigt man eine Idee, die auf das 19. Jahrhundert zurückgeht, und wir führen eine Science Fiction-artige Funktion ein: die Delta-Funktion.
. Um damit umzugehen, benötigt man eine Idee, die auf das 19. Jahrhundert zurückgeht, und wir führen eine Science Fiction-artige Funktion ein: die Delta-Funktion.
Ein kurzer Exkurs zu ![]() -Funktionen.
-Funktionen.
Betrachten wir die Heaviside-Funktion
![Rendered by QuickLaTeX.com \[H(x)= \begin{cases} 0,&x<a,\\ b, &x=a,\\ 1, &x>a, \end{cases}\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-44f2923c76248740f8eebe8527b13bf8_l3.png)
mit dem Graphen in Abbildung 5.
Deren Ableitung ist die Delta-Funktion im Punkt . Diese Ableitung ist gegeben durch
![Rendered by QuickLaTeX.com \[H'(x)= \delta(x)= \begin{cases} 0,&x<a,\\ +\infty, &x=a,\\ 0, &x>a, \end{cases}\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-592d89a3ca1b0fbf843489710612dd7e_l3.png)
Dies ist keine Funktion im herkömmlichen Sinn, sondern eine „verallgemeinerte Funktion“. Wenn aber weiterhin der Fundamentalsatz der Analysis gelten soll, erhält man
![]()
,
also ist das Integral ![]() gleich 1, was wiederum bedeutet, dass der Flächeninhalt unter dem „Graphen“ der Delta-Funktion 1 ist! Dieser Trick war unter den Physikern des 19. Jahrhunderts weit verbreitet und lieferte richtige Ergebnisse, forderte Mathematiker aber heraus, die auf der Suche nach Begründungen waren.. In den 1940er Jahren fand endlich Laurent Schwartz exakte Lösungen und nannte diese neuen „Rohlinge“ Distributionen.
gleich 1, was wiederum bedeutet, dass der Flächeninhalt unter dem „Graphen“ der Delta-Funktion 1 ist! Dieser Trick war unter den Physikern des 19. Jahrhunderts weit verbreitet und lieferte richtige Ergebnisse, forderte Mathematiker aber heraus, die auf der Suche nach Begründungen waren.. In den 1940er Jahren fand endlich Laurent Schwartz exakte Lösungen und nannte diese neuen „Rohlinge“ Distributionen.
Für ihn waren Distributionen keine Funktionen ![]() mit Werten an der Stelle
mit Werten an der Stelle ![]() , sondern „Dinge“, die stattdessen von ihren Durchschnittswerten bestimmt werden, die man als Integral der Distribution mal einer Gewichtung ansieht. Ein Beispiel aus der Realität wären Bilder, die von Fotoapparaten gemacht werden: Man kann das Licht messen, das auf einen Sensor trifft, dieser Sensor hat aber eine Größe, man kann nicht das Licht messen, das auf einen unendlich kleinen Punkt trifft.
, sondern „Dinge“, die stattdessen von ihren Durchschnittswerten bestimmt werden, die man als Integral der Distribution mal einer Gewichtung ansieht. Ein Beispiel aus der Realität wären Bilder, die von Fotoapparaten gemacht werden: Man kann das Licht messen, das auf einen Sensor trifft, dieser Sensor hat aber eine Größe, man kann nicht das Licht messen, das auf einen unendlich kleinen Punkt trifft.
Zurückgehend zur Beschreibung der Stoßwelle, mit Bezug auf Abbildung 2, müssen wir ![]() entlang der schrägen, kräftigen Linie oben rechts unstetig werden lassen. Die Burgersgleichung gilt immer noch, wenn man Delta-Funktionen benutzt und den Stoß selbst mit der Durchschnittsgeschwindigkeit der von links und rechts kollidierenden Autos bewegen lässt. Genau genommen muss man die Umgebung eines Punktes
entlang der schrägen, kräftigen Linie oben rechts unstetig werden lassen. Die Burgersgleichung gilt immer noch, wenn man Delta-Funktionen benutzt und den Stoß selbst mit der Durchschnittsgeschwindigkeit der von links und rechts kollidierenden Autos bewegen lässt. Genau genommen muss man die Umgebung eines Punktes ![]() betrachten, der sich in den Stößen befindet. Sei
betrachten, der sich in den Stößen befindet. Sei ![]() die Geschwindigkeit der Stoßwelle selbst, so dass die Stoßwelle tangential zur Geraden
die Geschwindigkeit der Stoßwelle selbst, so dass die Stoßwelle tangential zur Geraden ![]() ist. Die Gleichung dieser Geraden kann umgeschrieben werden als
ist. Die Gleichung dieser Geraden kann umgeschrieben werden als ![]() . Daraus ergeben sich Parallelen, die durch
. Daraus ergeben sich Parallelen, die durch ![]() gegeben sind, mit
gegeben sind, mit ![]() . In einem kleinen Maßstab kann man annehmen, dass die Geschwindigkeit auf jeder Seite des Stoßes (annähernd) konstant ist, und dass sie auf der linken Seite den Wert
. In einem kleinen Maßstab kann man annehmen, dass die Geschwindigkeit auf jeder Seite des Stoßes (annähernd) konstant ist, und dass sie auf der linken Seite den Wert ![]() und auf der rechten Seite den Wert
und auf der rechten Seite den Wert ![]() annimmt. Es ist also zu zeigen, dass
annimmt. Es ist also zu zeigen, dass
(4) ![]()
Da ![]() auf jeder Seite des Stoßes konstant ist, ist
auf jeder Seite des Stoßes konstant ist, ist ![]() entlang der Geraden
entlang der Geraden ![]() mit
mit ![]() konstant und daher hängt
konstant und daher hängt ![]() lediglich von dem Wert von
lediglich von dem Wert von ![]() ab. Wenn man
ab. Wenn man ![]() wählt, erlaubt das
wählt, erlaubt das ![]() für eine Funktion
für eine Funktion ![]() (mit einer Variablen!). (Der Graph dieser Funktion könnte so aussehen wie eine der hinteren Kurven in Abbildung 3.) Daher ist
(mit einer Variablen!). (Der Graph dieser Funktion könnte so aussehen wie eine der hinteren Kurven in Abbildung 3.) Daher ist ![]() . von der Form
. von der Form ![]() , wobei
, wobei ![]() eine Heaviside-Funktion in
eine Heaviside-Funktion in ![]() ist und
ist und ![]() .
.
Bemerkenswert ist, dass ![]() ist, womit die Burgersgleichung geschrieben werden kann als
ist, womit die Burgersgleichung geschrieben werden kann als
(5) ![]()
.
Da ![]() einen Größenunterschied
einen Größenunterschied ![]() hat, ist die Funktion
hat, ist die Funktion ![]() von der Form
von der Form ![]() . Damit ist
. Damit ist
![Rendered by QuickLaTeX.com \[\frac{d\left(\tfrac12 \widetilde{V}^2\right)}{dy}=\tfrac12 (V_R^2-V_L^2)\delta(y).\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-e4673520edc89c8f185142d8c1b03551_l3.png)
(6) 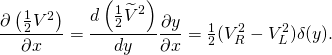
(7) ![]()
Ersetzen von (6) und (7) in (5) ergibt
![]()
was nur stimmen kann, wenn (4) erfüllt ist.
6. Zusatzmaterial 2 – Modellierung von Fluidfluss im Dreidimensionalen
Wir wollen den Fluss von Wasser modellieren, oder allgemeiner gesprochen, den Fluss von jeglicher inkompressibler Flüssigkeit. Wir haben bereits gesagt, dass Wasser sich an jedem Punkt ![]() mit einer Geschwindigkeit bewegt, die gegeben ist durch einen Vektor
mit einer Geschwindigkeit bewegt, die gegeben ist durch einen Vektor ![]() . Schon die drei Komponenten von
. Schon die drei Komponenten von ![]() sind drei unbekannte Funktionen, die es zu finden gilt. Tatsächlich werden wir aber eine vierte Funktion finden, den Druck
sind drei unbekannte Funktionen, die es zu finden gilt. Tatsächlich werden wir aber eine vierte Funktion finden, den Druck ![]() . Der Druck ist die Kraft (pro Fläche), die Erdbaumaschinen ihre Arbeit ermöglicht: eine Pumpe setzt ein Ölbehältnis unter Druck, das mit Schläuchen an die Kolben angeschlossen ist, die die Eimer, Schaufeln etc. antreiben. Der Druck in einem Fluid kommt durch die Kraft zustande, die auf ein Element seines Nachbarfluides ausgeübt wird. Im Allgemeinen sind Flüssigkeiten wie Wasser und Öl inkompressibel, das bedeutet, dass ihr Volumen sich nicht verändert, wenn sie zusammengedrückt werden, während Gase kompressibel sind. Um nun die Bewegung eines Fluides zu modellieren, beginnt man genau wie beim Verkehr: angenommen Wasser versucht seine Geschwindigkeit beizubehalten, seine Viskosität bewirkt aber, dass die Geschwindigkeit an jedem Punkt durchschnittlich die seiner Nachbarn beträgt. Dies kann durch Gleichung (2) dargestellt werden, wenn deren Bedingungen vektoriell interpretiert werden. Für den Term der Viskosität wird bzgl. der Dreidimensionalität die zweite Ableitung gebildet. Dieser Term beschreibt nun Funktionsänderungen als Durchschnitt der jeweiligen Nachbarn. Auf einer Straße gibt es zwei Nachbarn, einen davor und einen dahinter. Im Dreidimensionalen stellt man sich das als kleinen Würfel um einen Punkt im Wasser vor, dort gibt es sechs Nachbarn, einen davor, einen dahinter, einen links, einen rechts, einen darunter und einen darüber. Dies führt dazu, dass man anstatt eines Terms
. Der Druck ist die Kraft (pro Fläche), die Erdbaumaschinen ihre Arbeit ermöglicht: eine Pumpe setzt ein Ölbehältnis unter Druck, das mit Schläuchen an die Kolben angeschlossen ist, die die Eimer, Schaufeln etc. antreiben. Der Druck in einem Fluid kommt durch die Kraft zustande, die auf ein Element seines Nachbarfluides ausgeübt wird. Im Allgemeinen sind Flüssigkeiten wie Wasser und Öl inkompressibel, das bedeutet, dass ihr Volumen sich nicht verändert, wenn sie zusammengedrückt werden, während Gase kompressibel sind. Um nun die Bewegung eines Fluides zu modellieren, beginnt man genau wie beim Verkehr: angenommen Wasser versucht seine Geschwindigkeit beizubehalten, seine Viskosität bewirkt aber, dass die Geschwindigkeit an jedem Punkt durchschnittlich die seiner Nachbarn beträgt. Dies kann durch Gleichung (2) dargestellt werden, wenn deren Bedingungen vektoriell interpretiert werden. Für den Term der Viskosität wird bzgl. der Dreidimensionalität die zweite Ableitung gebildet. Dieser Term beschreibt nun Funktionsänderungen als Durchschnitt der jeweiligen Nachbarn. Auf einer Straße gibt es zwei Nachbarn, einen davor und einen dahinter. Im Dreidimensionalen stellt man sich das als kleinen Würfel um einen Punkt im Wasser vor, dort gibt es sechs Nachbarn, einen davor, einen dahinter, einen links, einen rechts, einen darunter und einen darüber. Dies führt dazu, dass man anstatt eines Terms ![]() drei Terme, nämlich:
drei Terme, nämlich:
![]()
hinzufügt. Dieser Ausdruck ist als Laplace-Operator von ![]() bekannt.
bekannt.
Ein weiteres Problem ist, dass der Fluss, der durch diese Gleichung gegeben ist, sich durch die Dichte des Wassers verstärken oder verringern kann, was der Inkompressibilität von Wasser widerspricht. Man muss also gewährleisten, dass an jedem Punkt, wenn man sich einen kleinen Würfel um den Punkt herum vorstellt, die Wassermenge, die hineinfließt, genauso groß ist wie die, die hinausfließt. Es gibt einen einfachen Weg, um das sicherzustellen: die Divergenz von ![]() muss stets Null sein. Wenn
muss stets Null sein. Wenn ![]() und
und ![]() sind, dann ist
sind, dann ist
![]()
Wenn man sich die Ableitung als Grenzwert vorstellt, besagt das Verschwinden der Divergenz:
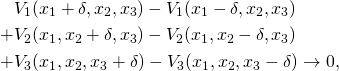
was bedeutet, dass der Wasserausfluss an jeder der sechs Seiten des kleinen Würfels dazu gezählt und der Wasserzufluss abgezogen wird, so dass es insgesamt Null ergibt.
Um abschließend sicherzustellen, dass die Divergenz von ![]() in der Strömung null bleibt muss eine zusätzliche Kraft hinzugefügt werden, die dadurch entsteht, dass Wassermoleküle, die sich „weigern“ zusammengedrückt zu werden, gegeneinander gedrückt werden. Der Widerstand gegen die Kompression wird durch den Druck gemessen, der Gradient des Drucks ist eine Kraft, die jedes Wasserelement beschleunigt, um die Dichte konstant zu halten.
in der Strömung null bleibt muss eine zusätzliche Kraft hinzugefügt werden, die dadurch entsteht, dass Wassermoleküle, die sich „weigern“ zusammengedrückt zu werden, gegeneinander gedrückt werden. Der Widerstand gegen die Kompression wird durch den Druck gemessen, der Gradient des Drucks ist eine Kraft, die jedes Wasserelement beschleunigt, um die Dichte konstant zu halten.
Euler- und Navier-Stokes-Gleichungen
Nun kann man all dies in die Gleichungen von einem inkompressiblen Fluss zusammentragen. Die Gleichung hat vier unbekannte Funktionen, die bestimmt werden müssen, die drei Komponenten ![]() und den Druck
und den Druck ![]() . Der Druck
. Der Druck ![]() wird für die Gewährleistung der Inkompressibilität benötigt. Die Navier-Stokes-Gleichung ist das System der vier Gleichungen:
wird für die Gewährleistung der Inkompressibilität benötigt. Die Navier-Stokes-Gleichung ist das System der vier Gleichungen:
![Rendered by QuickLaTeX.com \[\boxed{\begin{aligned} \frac{\partial V}{\partial t} + V \cdot \frac{\partial V}{\partial x}&= -\nabla p + \nu\triangle V \\ \text{div}(V) &=0 \end{aligned}}\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-c63352c5fb58a57d4894d6b382890372_l3.png)
( ![]() ist hier der Gradient von
ist hier der Gradient von ![]() , also
, also ![]() . Das Minuszeichen ist dadurch gerechtfertigt, dass die rechte Seite die Beschleunigung darstellt. Wenn der Druck steigt, wird
. Das Minuszeichen ist dadurch gerechtfertigt, dass die rechte Seite die Beschleunigung darstellt. Wenn der Druck steigt, wird ![]() kleiner und es ergibt sich eine negative Beschleunigung.) Der Spezialfall, bei dem die Viskosität
kleiner und es ergibt sich eine negative Beschleunigung.) Der Spezialfall, bei dem die Viskosität ![]() ist, heißt Eulergleichung. In Dimension 1 impliziert Inkompressibilität konstante Geschwindigkeit, daher gibt es keine Stöße. Es wurde bewiesen, dass es auch im Zweidimensionalen keine Stöße gibt, wenn eine Anfangsgeschwindigkeitsfunktion gegeben ist, so gibt es eine eindeutige Lösung, die für jede Zeit existiert. Im Dreidimensionalen erscheint die Wahrscheinlichkeit, dass Definitionslücken auftreten, ohne den bändigenden Effekt der Viskosität, deutlich größer – doch sicher weiß das niemand.
ist, heißt Eulergleichung. In Dimension 1 impliziert Inkompressibilität konstante Geschwindigkeit, daher gibt es keine Stöße. Es wurde bewiesen, dass es auch im Zweidimensionalen keine Stöße gibt, wenn eine Anfangsgeschwindigkeitsfunktion gegeben ist, so gibt es eine eindeutige Lösung, die für jede Zeit existiert. Im Dreidimensionalen erscheint die Wahrscheinlichkeit, dass Definitionslücken auftreten, ohne den bändigenden Effekt der Viskosität, deutlich größer – doch sicher weiß das niemand.
7. Bibliographie
1. A Mathematical Introduction to Fluid Mechanics, Alexandre Chorin and Jerrold Marsden, Springer 1993.
2. Wikipedia Artikel http://en.wikipedia.org/wiki/Burgers’_equation.
3. Nonlinear Partial Differential Equations for Scientists and Engineers, Lokenath Debnath, Birjauser-Boston, 2004.


 Deutsch
Deutsch 简体中文
简体中文  English
English  Français
Français  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português