Originating authors are David Mumford and Christiane Rousseau.
Foreword: This vignette is more difficult than others. However, in a few pages, it tells you how to explain in simple terms one of the most difficult open problems at the beginning of the 21st century. The vignette contains enrichment material, that you can choose to read or skip. The editors of the Klein blog hesitated for a while posting this vignette. After testing it with teachers during two Klein workshops, who expressed that they enjoy being challenged by more difficult vignettes, they decided to test it on the blog. They are eager to hear your comments, and if some of you were motivated by this topic.
You have probably heard some planes breaking the sound barrier. What does that mean? It means that a shock wave in the atmosphere is created as in Figure 1. But what is a shock wave? Imagine heavy traffic on highways as a wave. A shock wave corresponds to collisions. To explain this, we develop our intuition with a 1D model: traffic on a one lane road at different speeds. You know that collisions could occur if drivers do not adjust their speed. The atmosphere is a fluid, and traffic is a rough model of 1D fluid which is convenient to develop our intuition. Under which conditions do shock waves or other singularities occur in fluids? A million dollar prize is offered for answering this question. This is what we are going to explain you.
1. The 1-D models
Burger’s equation
Let us construct a simple traffic model. We have cars at each position ![]() along a line representing a road. At time
along a line representing a road. At time ![]() , the car at position
, the car at position ![]() has speed
has speed ![]() . The car starting at
. The car starting at ![]() will be at position
will be at position ![]() at time
at time ![]() . Let
. Let ![]() be the speed of the car at position
be the speed of the car at position ![]() and time
and time ![]() . The hypothesis is that cars move at constant speed along a straight road. Hence, we have
. The hypothesis is that cars move at constant speed along a straight road. Hence, we have ![]() , which means that this function is constant in
, which means that this function is constant in ![]() . Hence, its derivative should be identically zero! By the chain rule for functions of several variables we have
. Hence, its derivative should be identically zero! By the chain rule for functions of several variables we have
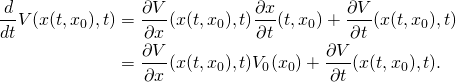
Simply writing that the position on the road is given by ![]() , and using that
, and using that ![]() , the traffic equation becomes what is called Burger’s equation:
, the traffic equation becomes what is called Burger’s equation:
(1) ![]()
This equation says that each car maintains a constant speed as it moves long the road.
Another way of saying this is that if a car at position ![]() starts off with speed
starts off with speed
![]() , then at time
, then at time ![]() it will be at position
it will be at position ![]() still with the same speed:
still with the same speed:
![]() for all
for all ![]() .
.
Of course this is not a great idea! Collisions will occur. Figure 2 shows one such resulting chaos.

Figure 2: A shock wave in Burger’s equation for the initial speed given by V(x)=exp(-x²). Shown are the world lines of cars initially equally spaced on the road. The heavy black line is where the collisions happen.
Describing the shocks
What happens when we approach the shock? Suppose that at the beginning (![]() ) two points
) two points ![]() had velocities
had velocities ![]() . Let us denote the position of
. Let us denote the position of ![]() at time
at time ![]() by
by ![]() . Similarly
. Similarly ![]() denotes the position of
denotes the position of ![]() at time
at time ![]() . Then
. Then ![]() gets closer and closer to
gets closer and closer to ![]() and just before the shock
and just before the shock ![]() is very close to
is very close to ![]() . Yet, the difference of their velocities
. Yet, the difference of their velocities ![]() has remained the same. This means that the mean slope of the function
has remained the same. This means that the mean slope of the function ![]() as a function of
as a function of ![]() for fixed
for fixed ![]() is becoming very large (see Figure 3 which shows the graph of
is becoming very large (see Figure 3 which shows the graph of ![]() as a function of
as a function of ![]() for several values of
for several values of ![]() ). Hence, we see that
). Hence, we see that ![]() is becoming infinite when we approach the shock. This means that our differential equation (1) has a singularity at the shock.
is becoming infinite when we approach the shock. This means that our differential equation (1) has a singularity at the shock.

Figure 3: In the same situation as figure 2, we show the graph of velocity as a function of space for six representative times. Note how the velocity becomes discontinuous when the shock wave develops: the slope of the velocity becomes infinite for fixed x, and also for fixed t.
2. Model real shocks or model how to avoid them?
We have modeled a situation in which all cars traveling along the road never change their speed. If the function ![]() is increasing with
is increasing with ![]() , then the cars in the front are faster that the ones behind, and there is no problem. But if some slower cars are ahead of the faster ones, there will be a crash if no one modifies their speed. There are two ways to develop the model further. Coming back to our initial motivation, the supersonic shock wave, we can refine our equation to include collisions, a one-dimensional version of shocks. The underlying cause is the same for supersonic planes, namely the air in front of the plane cannot travel fast enough to escape the plane coming up from behind! Or we can refine our equation to allow for more intelligent driver behavior, having the faster car slow down and slower car speed up.
, then the cars in the front are faster that the ones behind, and there is no problem. But if some slower cars are ahead of the faster ones, there will be a crash if no one modifies their speed. There are two ways to develop the model further. Coming back to our initial motivation, the supersonic shock wave, we can refine our equation to include collisions, a one-dimensional version of shocks. The underlying cause is the same for supersonic planes, namely the air in front of the plane cannot travel fast enough to escape the plane coming up from behind! Or we can refine our equation to allow for more intelligent driver behavior, having the faster car slow down and slower car speed up.
Smarter drivers
When a collision is imminent, the behavior of a driver with a brain would surely be influenced by his neighbors, tending to compromise his speed with that of his neighbors. The analogy is to think of a viscous fluid: if you have observed honey flowing, you may have remarked that it behaves as a whole, as if all parts were tied together: no drops are splashing around, they stay linked to the main stream. Water has viscosity about 10,000 times less and air 50 less than that — but not zero. So one possible correction to Burger’s equation which avoids collisions when the initial function speed ![]() is bounded will involve adding viscosity term. Such a term is just a multiple of the second derivative
is bounded will involve adding viscosity term. Such a term is just a multiple of the second derivative ![]() . Hence, a modified equation takes the form which is known as the viscous Burger’s equation:
. Hence, a modified equation takes the form which is known as the viscous Burger’s equation:
(2) ![]()
with ![]() being called the viscosity. The modified world lines can be seen in Figure 4 for the same function
being called the viscosity. The modified world lines can be seen in Figure 4 for the same function ![]() describing the initial speed as in Figure 2.
describing the initial speed as in Figure 2.

Figure 4: In the same situation as Figure 2, we add some viscosity. Note how the cars bunch up but do not collide any more. On the right, we see the graph of V(x,t).
Why a second derivative? Recall that the second derivative is the limit of
(3) ![]()
You can see this because it is the first derivative of the first derivative so will be close to
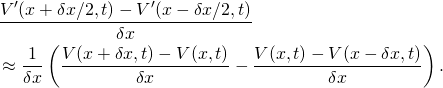
Let us rewrite this expression as
![]()
What means the second factor? It is a mean of two terms: the first is the difference of speed in the front and in the middle and the second is the difference of speed in the back and in the middle. The danger of a collision is when ![]() . In that case, the first term is negative and the second is positive. If the first term wins, the mean is negative and expression (3) tells you that you should break, since the left hand side is the acceleration. If the second term wins, then the mean is positive and you should accelerate.
. In that case, the first term is negative and the second is positive. If the first term wins, the mean is negative and expression (3) tells you that you should break, since the left hand side is the acceleration. If the second term wins, then the mean is positive and you should accelerate.
Just before a collision happens, there will be a discontinuity in velocity with a faster car about to hit a slower one.
Adding the viscosity removes the shocks in Burger’s equation! We can now move to tell you about the million dollar prizes.
Note that for ![]() fixed, the left hand side represents the acceleration, since it is the derivative of the function
fixed, the left hand side represents the acceleration, since it is the derivative of the function ![]() with respect to
with respect to ![]() . So the modified viscous equation says that if the middle car is slower than the average speed of its neighbors ahead and behind, then it accelerates. If it is faster, then it decelerates.
. So the modified viscous equation says that if the middle car is slower than the average speed of its neighbors ahead and behind, then it accelerates. If it is faster, then it decelerates.
3. The challenges of modeling the real world flows
The real world flows being modeled
We have been cheating a bit to make nice clean math out of a definitely messier real world. In particular, we have neglected bringing in the density of the cars on the road. Better traffic models like the Lighthill-Whitham-Richards model deal with local average density ![]() and as well as local average speed
and as well as local average speed ![]() . But versions of Burger’s equation still dominate these refined models so our discussion was basically ok.
. But versions of Burger’s equation still dominate these refined models so our discussion was basically ok.
The motion of air around a plane, especially around its wings, and the motion of water around a boat are real world applications of much greater interest. Mathematicians have worked on modeling the latter ever since Euler in the 18th century. Air and water are fundamentally different because water is almost completely incompressible while air is highly compressible. The incompressibility of oil is used for example to transmit tremendous forces in machines like bulldozers and backhoes. The million dollar prize concerns the incompressible case in three dimensions.
The million dollar prizes
In order to celebrate mathematics in the new millennium, Landon T. Clay established seven Prize Problems. The Prizes were conceived to record some of the most difficult problems with which mathematicians were grappling at the turn of the second millennium as well as to elevate in the consciousness of the general public the fact that in mathematics, the frontier is still open and abounds in important unsolved problems. A prize of 1 million dollars will be given for the solution of each problem — and one of them (the Poincaré conjecture) has been solved so far!
The 1 million dollar prize which interests us is concerned with the equations governing the flow of an incompressible fluid with viscosity in 3-dimensional space: these equations are called the Navier-Stokes equations, named after Claude-Louis Navier (1785–1836) and George Gabriel Stokes, (1819–1903) who worked on the motion of fluids. Except for the incompressibility which we will explain below, they are simply the three dimensional version of Burger’s equation with viscosity.
What’s the scoop? Most mathematicians conjecture that these Navier-Stokes equations never form shocks or other singularities like turbulence with eddies of all sizes, big to infinitesimal. Thus the equations should be solvable for time progressing as far as you want. If you prove that, the check is yours! But in science we are never sure of the conclusion before it is proved. Hence, if you can exhibit an example of initial conditions creating a shock or other singularity in finite time, the check is also yours. Why do mathematicians believe that no shock or other singularity will develop in Navier-Stokes equation? This was proven to be the case for 2-dimensional flows decades ago by a Russian woman, Olga Ladyzhenskaya. Since then, numerical simulations have not suggested that any singularities develop in the 3-dimensional case either. The simulation of solutions of partial differential equations like these is a huge computational challenge requiring sophisticated algorithms and programs running for long periods on very powerful computers.
Is that a contradiction with the shock wave of Figure 1? No! Air is compressible and the million dollar prize concerns incompressible flows.
The rest of this vignette is an enrichment for you, in two directions. In the first one, we explain how we allow singular solutions for Burger’s equation. (see section 5. READ MORE 1) If you have still remembered your multivariate calculus course, you can read how we modify Burger’s equation to model the movements of incompressible fluids in ![]() -dimensional space (see section 6. READ MORE 2).
-dimensional space (see section 6. READ MORE 2).
4. Conclusion
What have we learnt? Many things. For instance, you could have imagined that modeling a fluid was so complex that you could not understand it. Now you have realized that it only involves the same basic principles of mechanics that you may have seen when studying forces, Newton laws, and conservation of energy. Also, the tools to express these physical laws simply involve the notions introduced in a multivariate calculus course. The form of the equations governing the motion of a fluid are very simple. Yet, there are many open questions about their solutions, even if they have been intensively studied, both theoretically and numerically, for more than 200 years.
If you have read the modeling of shocks, you have seen an important facet of the work of the mathematician. When solutions of a problem do not exist, the mathematician can create an object which is a solution. You are familiar with the creation of the complex numbers so as to add to ![]() the roots of any polynomial with real coefficients. Here, the mathematicians have created the distributions, thus allowing the partial differential equations (PDE) to have weak solutions.
the roots of any polynomial with real coefficients. Here, the mathematicians have created the distributions, thus allowing the partial differential equations (PDE) to have weak solutions.
But this has not sufficed to settle the million dollar prize described above. Let us quote Charles L. Fefferman describing the prize on the Clay website: “…, our understanding is at a very primitive level. Standard methods from PDE appear inadequate to settle the problem. Instead, we probably need some deep, new ideas.” Maybe one of your students will make the breakthrough some day…
5. READ MORE 1 – Going back to Burger’s equation
Allowing singular solutions
But shocks do exist in practice! As a scientist, we cannot just stop our analysis here. A “singularity” is a very rich phenomenon and the mathematician has no choice but to put on his or her mathematical glasses and think more deeply about this behavior in the context of the equation. This approach is called introducing generalized or `weak’ solutions that are not smooth. In our case, cars with distinct speeds are colliding. Think of this as a huge pile-up of ever more cars speeding in from the left with the pile-up moving fast enough to collide with ever more cars on the right. Thus we want to allow ![]() be discontinuous in
be discontinuous in ![]() , having one limit on the left and another from the right.
, having one limit on the left and another from the right.
But the equation uses derivatives of ![]() . To deal with these, we need an idea which goes back to the 19th century and introduce a science-fiction kind of function called a delta function.
. To deal with these, we need an idea which goes back to the 19th century and introduce a science-fiction kind of function called a delta function.

Figure 5: Heaviside and delta functions.
A short digression on ![]() functions.
functions.
Consider the Heaviside function
![Rendered by QuickLaTeX.com \[H(x)= \begin{cases} 0,&x<a,\\ b, &x=a,\\ 1, &x>a, \end{cases}\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-44f2923c76248740f8eebe8527b13bf8_l3.png)
with graph in Figure 5.
Its derivative is the delta function at the point ![]() . Note that this derivative is given by
. Note that this derivative is given by
![Rendered by QuickLaTeX.com \[H'(x)= \delta(x)= \begin{cases} 0,&x<a,\\ +\infty, &x=a,\\ 0, &x>a, \end{cases}\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-592d89a3ca1b0fbf843489710612dd7e_l3.png)
so it is not a function in the general sense, but only a “generalized function”.
Yet, if the fundamental theorem of calculus were to remain true, we should have
![]()
i.e. the delta function is infinite exactly enough so that the integral ![]() is equal to 1, that is the area under the “graph” of
is equal to 1, that is the area under the “graph” of ![]() is 1! This trick was used widely by the physicists in the 19th century and provided correct answers, thus challenging the mathematicians in search of rigor. It could finally be made rigorous in the 1940s by Laurent Schwartz, who called these new beasts, distributions.
is 1! This trick was used widely by the physicists in the 19th century and provided correct answers, thus challenging the mathematicians in search of rigor. It could finally be made rigorous in the 1940s by Laurent Schwartz, who called these new beasts, distributions.
To make the thing work, he said distributions aren’t functions ![]() with values at points
with values at points
![]() , but they are “things” determined instead by their average values, which you think of as the integral of the distribution times a weighting function. A real life example is given by images made by cameras: you can measure light hitting a sensor but the sensor has a size; you can’t measure the light hitting an infinitesimal point.
, but they are “things” determined instead by their average values, which you think of as the integral of the distribution times a weighting function. A real life example is given by images made by cameras: you can measure light hitting a sensor but the sensor has a size; you can’t measure the light hitting an infinitesimal point.
Back to describing our shock wave, referring to Figure 2, we must let ![]() be discontinuous across the bold slanting line at the top right. Burger’s equation will still hold if you use delta functions and make the shock itself move at the average of the speeds of the cars colliding from the left and the right. In fact, look near a point
be discontinuous across the bold slanting line at the top right. Burger’s equation will still hold if you use delta functions and make the shock itself move at the average of the speeds of the cars colliding from the left and the right. In fact, look near a point ![]() on the locus of shocks. Let
on the locus of shocks. Let ![]() be the speed of the shock wave itself so that the shock wave is tangent to a line
be the speed of the shock wave itself so that the shock wave is tangent to a line ![]() . The equation of this line can also be written as
. The equation of this line can also be written as ![]() . Hence parallel lines are given by
. Hence parallel lines are given by ![]() with
with ![]() . On a small scale we can suppose that the speed is (approximately) constant on each side of the shock, and that it takes the value
. On a small scale we can suppose that the speed is (approximately) constant on each side of the shock, and that it takes the value ![]() on the left of the shock, and
on the left of the shock, and ![]() on the right. So we need to show that
on the right. So we need to show that
(4) ![]()
Since ![]() is constant on each side of the shock, then
is constant on each side of the shock, then ![]() is constant along the lines
is constant along the lines ![]() with
with ![]() , and hence, that
, and hence, that ![]() depends only on the value of
depends only on the value of ![]() . If we let
. If we let ![]() , this allows to write
, this allows to write ![]() for some (one variable!) function
for some (one variable!) function
![]() . (The graph of this function could look like one of the back curves in Figure 3.) Hence,
. (The graph of this function could look like one of the back curves in Figure 3.) Hence, ![]() is of the form
is of the form ![]() , where
, where ![]() is a Heaviside function at
is a Heaviside function at ![]() , and
, and ![]() .
.
Note that ![]() , which allows to write Burger’s equation as
, which allows to write Burger’s equation as
(5) ![]()
Since ![]() has a jump of size
has a jump of size ![]() , the function
, the function ![]() is of the form
is of the form ![]() . Hence,
. Hence,
![Rendered by QuickLaTeX.com \[\frac{d\left(\tfrac12 \widetilde{V}^2\right)}{dy}=\tfrac12 (V_R^2-V_L^2)\delta(y).\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-e4673520edc89c8f185142d8c1b03551_l3.png)
Since ![]() then, by the chain rule,
then, by the chain rule,
(6) 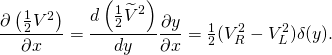
(7) ![]()
Replacing (6) and (7) in (5) yields
![]()
which can only be true if (4) is satisfied.
6. READ MORE 2 – Modeling the flow of a fluid in ![]() dimensions
dimensions
We want to model the flow of water, or more generally, the flow of any incompressible liquid. We already said that the water at each point ![]() is moving with speed given by a vector
is moving with speed given by a vector ![]() . Already the three components of
. Already the three components of ![]() are three unknown functions that we need to find. But actually we will need a fourth function, the pressure
are three unknown functions that we need to find. But actually we will need a fourth function, the pressure ![]() . The pressure is that force that enables earth-moving equipment to do their work: a pump pressurizes a reservoir of oil which is linked by hoses to the pistons which move the buckets, shovels, etc. The pressure in a fluid comes from the force exerted on an element of a fluid from its neighbors. In general liquids like water and oil are incompressible, i.e. their volume does not change when compressed while gases are compressible. Now, to model the movement of a fluid, start with the same idea as traffic: assume the water tries to retain its velocity as time progresses but viscosity is causing the velocity at each point to average out with that of its neighbors. This can be expressed by equation (2) if we interpret its terms vectorially.
. The pressure is that force that enables earth-moving equipment to do their work: a pump pressurizes a reservoir of oil which is linked by hoses to the pistons which move the buckets, shovels, etc. The pressure in a fluid comes from the force exerted on an element of a fluid from its neighbors. In general liquids like water and oil are incompressible, i.e. their volume does not change when compressed while gases are compressible. Now, to model the movement of a fluid, start with the same idea as traffic: assume the water tries to retain its velocity as time progresses but viscosity is causing the velocity at each point to average out with that of its neighbors. This can be expressed by equation (2) if we interpret its terms vectorially.
For the viscosity term we need the three dimensional way of adding a second derivative term. Now this term is supposed to say some function changes in the direction of being an average of its neighbors. On a road, you had two neighbors, one behind you and one in front. In three dimensions, thinking of this small cube around a point in the water, you have six neighbors, one to the left, one to the right, one in front, one behind, one above and one below. The effect of this is that instead of adding one term ![]() , you need to add three terms, namely:
, you need to add three terms, namely:
![]()
an expression known as the laplacian of ![]() .
.
Another problem is that the flow given by this equation may increase or decrease the density of the water, contradicting the fact that water is incompressible. What we need is that at any point, if we imagine a small cube around the point, the amount of water coming into the cube equals the amount of water going out. There’s a very simple way of ensuring this: the divergence of ![]() must be zero at all times. If
must be zero at all times. If ![]() and
and ![]() , then
, then
![]()
If we think of the derivative as a limit, the vanishing of the divergence says:
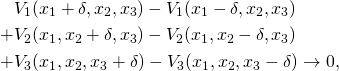
which amounts to adding up the water outflow and minus the water inflow at each of the six faces of the small cube and making it zero.
Finally to ensure that, under the flow, the divergence of ![]() stays zero, we need to add an additional force, which is caused by the water molecules pushing against each other, refusing to compress. The resistance to compression is measured by the pressure and the gradient of the pressure is a force which accelerates each bit of the water so as to maintain constant density.
stays zero, we need to add an additional force, which is caused by the water molecules pushing against each other, refusing to compress. The resistance to compression is measured by the pressure and the gradient of the pressure is a force which accelerates each bit of the water so as to maintain constant density.
Euler’s and Navier-Stokes’ equations
We are now ready to put all this together in the equations of an incompressible flow. The equation has four unknown functions which must be solved for, the three components ![]() and the pressure
and the pressure ![]() . The pressure must be there to ensure incompressibility. The Navier-Stokes equation is the system of four equations:
. The pressure must be there to ensure incompressibility. The Navier-Stokes equation is the system of four equations:
![Rendered by QuickLaTeX.com \[\boxed{\begin{aligned} \frac{\partial V}{\partial t} + V \cdot \frac{\partial V}{\partial x}&= -\nabla p + \nu\triangle V \\ \text{div}(V) &=0 \end{aligned}}\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-c63352c5fb58a57d4894d6b382890372_l3.png)
(Here ![]() is just the gradient of
is just the gradient of ![]() , namely the vector
, namely the vector ![]() . The minus sign is justified by the fact that the left hand side represents the acceleration. If the pressure increases then
. The minus sign is justified by the fact that the left hand side represents the acceleration. If the pressure increases then ![]() decelerates and we get a negative acceleration.) The special case where the viscosity
decelerates and we get a negative acceleration.) The special case where the viscosity ![]() is called Euler’s equation. In dimension 1, incompressibility implies that the speed is constant, and hence there are no shocks. It has been proved that there are also no shocks in dimension 2 and, given any initial speed function, there is a unique solution that exists for infinite time. In dimension 3, without the taming effect of viscosity, the likelihood that singularities develop appears much greater — but nobody knows for sure.
is called Euler’s equation. In dimension 1, incompressibility implies that the speed is constant, and hence there are no shocks. It has been proved that there are also no shocks in dimension 2 and, given any initial speed function, there is a unique solution that exists for infinite time. In dimension 3, without the taming effect of viscosity, the likelihood that singularities develop appears much greater — but nobody knows for sure.
7. Bibliography
1. A Mathematical Introduction to Fluid Mechanics, Alexandre Chorin and Jerrold Marsden, Springer 1993.
2. Wikipedia article http://en.wikipedia.org/wiki/Burgers’_equation.
3. Nonlinear Partial Differential Equations for Scientists and Engineers, Lokenath Debnath, Birjauser-Boston, 2004.

