Gabriel Rosenberg e Mark Iwen
7 Giugno 2012
È un fatto poco conosciuto che, nelle Olimpiadi invernali del 2002, siano state assegnate due medaglie d’oro per la stessa competizione di pattinaggio di figura a coppie. Queste due medaglie sono state alla fine il risultato di un votazione contenziosa che inizialmente risultava nei chiari favoriti del pubblico che non hanno vinto la medaglia d’oro. L’oltraggio su questa decisione è stato così grande che, alla fine, il Comitato Olimpico Internazionale (COI) ha dovuto, per calmare lo scandalo, assegnare una seconda medaglia d’oro alla coppia di pattinaggio di figura che si trovava al secondo posto.
Come risultato secondario, è stato cambiato il sistema di voto, per decidere quali pattinatrici di figura meritino quali medaglie. (N.B. Prima del 2003, i giudici assegnavano individualmente il punteggio ai partecipanti e usavano questi risultati per classificare gli atleti. Queste classifiche (non punteggi) venivano poi combinate per assegnare i premi nel complesso).
Immagina di essere nel Comitato Olimpico Internazionale del 2003 e che ti sia stato chiesto di sviluppare un sistema di voto migliore per giudicare le competizioni di pattinaggio di figura in futuro. Quali sistema di voto sceglieresti per classificare i pattinatori di figura? Come potresti essere sicuro che il sistema di voto sia equo? Senza sorpresa, la matematica può aiutarci a rispondere a queste domande.
Funzioni alla riscossa: il potere dell’astrazione
Un modo di pensare come creare un nuovo sistema di voto per giudicare i pattinatori di figura (o un nuovo sistema di voto per un qualsiasi altro scopo) è di iniziare a considerare tutti i possibili sistemi di voto. Possiamo allora costruire un buon sistema di voto restringendo lentamente tutti i possibili sistemi fino ad un sistema minimo di alternative desiderabili. Procedendo in questo modo possiamo sperare di non mancare molte buone alternative, mantenendo quindi le nostre opzioni più aperte possibili.
Iniziamo questo processo modellizzando (un insieme molto generale) di tutti i possibili sistemi di voto. In questo scenario, un qualunque sistema di voto finisce per riguardare la classificazione di un insieme di pattinatori basato sull’input fornito da un insieme di votanti (ad esempio i giudici olimpici).
Supponiamo che il nostro insieme di pattinatori in competizione sia ![]() , ad ognuno dei quali sia assegnato un punteggio da ciascun giudice, preso dal seguente insieme di giudici
, ad ognuno dei quali sia assegnato un punteggio da ciascun giudice, preso dal seguente insieme di giudici
![]()
![]()
Ogni giudice assegna punteggi ai pattinatori, il che produce una classifica diversa dei pattinatori per ogni giudice. Per esempio, i punteggi di un giudice per una particolare competizione possono risultare nelle seguenti classifiche individuali (si veda Tabella 1).
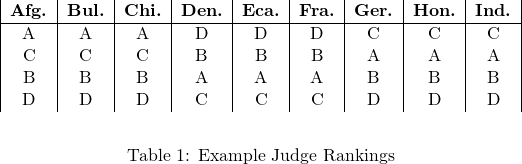
Figura 1: Un esempio delle classifiche dei giudici
Un qualunque sistema di voto deve prendere questo insieme di nove classifiche individuali da ogni giudice e restituire una classifica finale che determina i vincitori al primo posto (oro), al secondo (argento), al terzo (bronzo), al quarto, al quinto e così via dall’insieme ![]() di tutti i pattinatori. Matematicamente possiamo vedere che i nostri sistemi di voto sono esattamente l’insieme delle funzioni che prendono classifiche
di tutti i pattinatori. Matematicamente possiamo vedere che i nostri sistemi di voto sono esattamente l’insieme delle funzioni che prendono classifiche ![]() di S come input e producono una classifica finale di S come output. Qui
di S come input e producono una classifica finale di S come output. Qui ![]() rappresenta il numero dei giudici in
rappresenta il numero dei giudici in ![]() .
.
Alcune qualità che un buon sistema di voto dovrebbe avere
Certamente, possiamo immediatamente vedere che questo insieme di funzioni è troppo generale per essere equo. Per esempio, la funzione che assegna sempre al secondo pattinatore (cioè, in questo caso, Berezhnaya) una medaglia d’oro indipendentemente da come i giudici votino davvero è ancora un sistema di voto possibile. Chiaramente, dobbiamo restringere ulteriormente le nostre possibili funzioni di voto allo scopo di squalificare tali sistemi iniqui di voto.
Rispettando opinioni unanimi: la condizione Pareto
La condizione Pareto è una qualità che secondo la maggior parte delle persone dovrebbe possedere un buon sistema di voto. Approssimativamente, la condizione Pareto ci dice che se a un particolare pattinatore è assegnato un punteggio superiore a quello di un altro da tutti i giudici, allora un buon sistema di voto dovrebbe alla fine classificare il pattinatore preferito all’unanimità su tutti gli altri (per esempio, se Cohen è classificato sopra a Berezhnaya da tutti i giudici, allora Cohen dovrebbe classificarsi davanti a Berezhnaya sul podio). Questa condizione all’incirca garantisce che un sistema di voto rispetterà le opinioni unanimi dei votanti.
Sebbene sia difficile concepire un sistema di voto naturale che possa portare ad un risultato che non piace a nessuno dei votanti, ciò può realmente accadere quando il sistema di voto è gerarchico per natura. Consideriamo per esempio che i nostri quattro pattinatori si presentino nel seguente ordine: Asada, Dijkstra, Cohen, Berezhnaya. Asada e Dijkstra sono i primi due a pattinare e dopo di loro i giudici preferiscono Asada per un margine di 6-3.
Poi, dopo che ha pattinato Cohen i giudici votano di nuovo Cohen come pattinatore migliore rispetto ad Asada per un margine di 6-3. Alla fine, pattina Berezhnaya e, piuttosto sicuri, i giudici credono che Berezhnaya sia migliore di Cohen per un chiaro margine di 6-3. Un sistema di voto basato su questi confronti di coppia sequenziali potrebbe allora portare ad una classifica sul podio di: Berezhnaya (oro), Cohen (argento), Asada (bronzo), Dijkstra (non si posiziona). Quando i giudici, tuttavia, scrivono le loro classifiche di preferenza individuali, sono scioccati dallo scoprire che tutti e nove hanno pensato che Dijkstra abbia pattinato meglio di Berezhnaya (come si vede nella Tabella 2 dove ogni colonna rappresenta una classifica dei giudici dalla posizione più alta in cima a quella più bassa al fondo). La medaglia d’oro è andata ad un pattinatore che, all’unanimità, è stato giudicato peggiore di colui che ha concluso in quarta posizione!
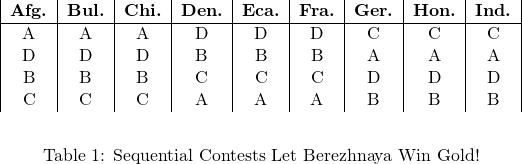
Figura 2: I contesti sequenziali fanno vincere l’ oro a Berezhnaya!
L’indipendenza delle alternative irrilevanti
Immaginiamo la seguente situazione: supponiamo che Asada e Berezhnaya si siano esibiti, ma Cohen non ancora. In questa situazione i giudici hanno tutti deciso quali dei primi due pattinatori preferiscono, tuttavia non sono ancora sicuri di come Cohen potrà essere paragonata dal momento che non si è ancora esibita. Gli addetti alla tabulazione dei risultati, comunque, vogliono conoscere la situazione attuale in questo momento (ad esempio, prima di una pausa pubblicitaria). Così, i funzionari dicono ai giudici di votare, per il momento, Cohen, in base alle loro migliori congetture di come lei si esibirà così che i funzionari possono annunciare come Asada risulterà rispetto a Berezhnaya.
La votazione viene considerata e il suo esito stabilisce che Asada dovrebbe essere davanti a Berezhnaya sul podio. La votazione, inoltre, fa posizionare Cohen da qualche parte sul podio, ma tutti sanno che la classifica è solo una supposizione che probabilmente cambierà una volta che Cohen si sarà effettivamente esibita.
Poi, dopo lo spot pubblicitario, Cohen pattina e alcuni dei giudici cambianole loro schede alla luce di come Cohen si è esibita. Non cambiano, comunque, se hanno dato una votazione maggiore a Asada rispetto a Berezhnaya o viceversa. Quando i risultati ufficiali sono raccolti attraverso la funzione di voto, però, si scopre ora che Berezhnaya finisce davanti a Asada sul podio! Questo sembra ingiusto! Perchè il piazzamento di Cohen dovrebbe determinare quale degli altri due pattinatori sia stato migliore? Un sistema in cui non può accadere questo strano comportamento si dice che soddisfa l’Indipendenza delle Alternative Irrilevanti, o IAI in breve. Generalmente, un sistema di voto che soddisfa alla IAI non cambierà, in base alle successive performance, le classifiche parziali precedentemente stabilite.
Opinione migliorate non dovrebbero mai offendere: monotonia
In seguito, immaginate una situazione in cui gli esiti delle medaglie sono stati annunciati con Asada che vince l’oro, Berezhnaya l’argento e Cohen il bronzo. Ma il giudice bulgaro, poi, si fa avanti e afferma che il suo voto è stato frainteso. Il suo voto è stato letto come: Asada, Berezhnaya, Cohen anche se lei abbia votato, in realtà, Berezhnaya, Asada, Cohen. I funzionari ricalcolano i punteggi e annunciano che ora Berezhnaya può avere solo il bronzo.
Questo sembra alquanto strano – ricevere un punteggio più alto da un giudice, in qualche modo, ha danneggiato Berezhnaya nei risultati del podio! Si dice che un sistema, per cui una tale situazione bizzarra non può mai accadere, soddisfa la monotonia.
A prima vista, può sembrare strano persino considerare una tale proprietà. Che tipo di sistema di voto porterebbe al fatto che un pattinatore sia penalizzato dal ricevere un punteggio più alto? Richiamiamo, comunque, che un sistema di voto potenziale è semplicemente una funzione e non c’è nulla che le richieda di essere ragionevole all’interno del contesto. Spetta a noi capire cosa rende il sistema ragionevole.
È interessante notare, però, che questa proprietà apparentemente ragionevole non è soddisfatta da alcuni dei sistemi di voto più comuni. In effetti, ogni sistema che usi una serie di elezioni con ballottaggio, come un sistema di voto usato dal COI per scegliere una città che ospiti le Olimpiadi, fallisce nel soddisfare la monotonia. Quanto frequentemente tali situazioni non monotone si verifichino davvero è il soggetto di molta ricerca e di molto dibattito, ma proprio il fatto che una tale situazione sia possibile in un sistema di voto in uso attuale, può portarci alla ricerca di un sistema di voto differente.
Uguaglianza: Neutralità e Anonimato
Un’altra proprietà che vorremmo che il nostro sistema avesse, in termini di equità, è che tratti ugualmente tutti i pattinatori. Cioè, gli stessi individui dovrebbero vincere indipendentemente dal loro ordine di esibizione, dai loro nomi, dalla loro nazionalità, etc. Definiremo neutrale un sistema che soddisfa a queste caratteristiche. In modo analogo, noi possiamo volere che il sistema di voto tratti ugualmente tutti i giudici. Vale a dire, la misura in cui il voto di un qualunque giudice conta nel determinare la classifica finale di un pattinatore non dovrebbe anch’essa dipendere dall’ordine di votazione dei giudici, dal loro nome, dalla loro nazionalità, etc. Si dice che un sistema di voto che soddisfa questa proprietà possiede l’anonimato.
Abbastanza sorprendentemente, possiamo scoprire sistemi di voto (democratici!) comuni che non soddisfano tali proprietà. Ad esempio, ogni nazione che nomina il suo capo, sulla base dell’accumulazione dei risultati delle elezioni da distretti geograficamente diversi, fallisce nel soddisfare l’anonimato. Ad esempio, negli Stati Uniti, gli elettori degli stati che hanno un supporto maggioritario per una parte politica, potrebbero avere voti che “contano per più” voti, riposizionandoli temporaneamente in un altro stato con una votazione più fortemente contestata. Ciò è dovuto esattamente al fatto che gli elettori dello “stato altalena” hanno più potere per influenzare quali candidati ottengano i voti elettorali del loro stato.
Alcune cattive notizie: il teorema di Arrow
Ora, abbiamo svariati criteri ragionevoli che vorremmo che il nostro sistema di voto Olimpico soddisfacesse. In questa sezione, proveremo a individuare un insieme di sistemi di voto buoni che hanno tutte le proprietà che abbiamo discusso sopra. Come prima, ci focalizzeremo su un pannello di nove giudici che classificano tre pattinatori.
Supponiamo di decidere di testare un nuovo sistema di voto, il quale ci viene detto che soddisfa le condizioni di IAI, monotonia e neutralità. Per aiutarci a testare questo nuovo sistema, consideriamo un caso, in cui ci sono tre insiemi di giudici. Diciamo che i tre giudici provenienti dalle nazioni asiatiche preferiscano tutti che i tre pattinatori migliori finiscano nell’ordine Asada, Berezhnaya, Cohen.
Inoltre, supponiamo che i due giudici americani preferiscano che i pattinatori si posizionino nell’ordine Cohen, Asada, Berezhnaya. Infine, diciamo che i quattro giudici europei preferiscano che i pattinatori finiscano nell’ ordine Berezhnaya, Cohen, Asada. Il nostro sistema di voto deve restituire un qualche ordine per il podio, ma quale può essere questo ordine?
Continuando il nostro esempio, supponiamo che il nostro buon sistema di voto produca un ordine del podio con Berezhnaya che finisce davanti ad Asada. Poiché noi sappiamo che il nostro sistema di voto soddisfa la IAI, questo implica che ogni volta che i quattro giudici europei classificano Berezhnaya davanti ad Asada, e gli altri cinque giudici classificano Asada davanti a Berezhnaya, dobbiamo finire con Berezhnaya davanti ad Asada sul podio (vale naya si posiziona rispetto ad Asada!). Poiché sappiamo che il nostro sistema di voto è monotono, certamente, questo risultato si verificherebbe ancora,anche se alcuni degli altri cinque giudici classificassero Berezhnaya davanti a Asada (cioè, fare così dovrebbe solo migliorare la posizione di Berezhnaya!).
Questo significherebbe che i quattro giudici europei detengono qualche potere dittatoriale nel senso che OGNI VOLTA CHE classificano Berezhnaya davanti a Asada, si garantiscono che Berezhnaya finirà davanti a Asada. Poiché abbiamo assunto che il nostro sistema di voto sia neutrale, non c’è niente di speciale, in questo esempio, riguardo a Berezhnaya e ad Asada. OGNI VOLTA CHE i giudici europei classificano un pattinatore davanti ad un altro, i pattinatori DEVONO finire in quell’ordine sul podio. Così, se i giudici europei votano in blocco (tutti loro votano allo stesso modo) il risultato del podio si accorderà con il loro voto a prescindere da come ogni altro blocco ha votato. Noi diremmo che i giudici europei hanno avuto potere dittatoriale.
Come risultato della nostra discussione nel paragrafo precedente, potremmo sostenere che il profilo sopra non dovrebbe avere come risultato il fatto che Berezhnaya finisca davanti ad Asada sul podio. Supponiamo, invece, che Asada debba finire davanti a Berezhnaya. Tuttavia, non possiamo vedere dove dovrebbe posizionarsi Cohen rispetto a Berezhnaya. Se l’ordine del podio avesse Cohen davanti a Berezhnaya, allora saremmo nella situazione in cui i due giudici americani sono gli unici che hanno classificato Cohen davanti a Berezhnaya (risultato sul podio nell’ordine che riflette la loro opinione).
Usando lo stesso ragionamento che abbiamo usato prima con i giudici europei, questo implicherebbe che i giudici americani hanno avuto potere dittatoriale! Se non vogliamo che una minoranza abbia potere dittatoriale, siamo costretti a posizionare sul podio, Asada davanti a Berezhnaya e quest’ ultimo, a sua volta, davanti a Cohen. Ma, questo implica che Asada finisca davanti a Cohen. Dato che i tre giudici asiatici erano gli unici che avevano, nelle loro classifiche, Asada davanti a Cohen, lo stesso processo di ragionamento che abbiamo usato con i giudici europei, ora mostrerebbe che i giudici asiatici hanno potere dittatoriale. La dittatura è inevitabile!
Poiché, per questo profilo, il nostro sistema di voto deve condurre a qualche classifica del podio, uno dei nostri tre gruppi di giudici deve avere potere dittatoriale.
Vale a dire, in ciascuna singola situazione in cui quel gruppo vota in blocco con le stesse classifiche, il risultato del podio concorderà con il loro voto. Questo è abbastanza negativo per il fatto che avremmo un gruppo costituito da una minoranza di giudici che avrebbe il potere, lavorando insieme per poter controllare i risultati del sistema di voto. Il problema, però, è persino peggiore. Una volta che abbiamo un gruppo dittatoriale potremmo ulteriormente dividere quel gruppo in due sottogruppi e, usando un ragionamento simile a quello sopra, mostrare che uno di quei sottogruppi è dittatoriale.
Continuando ulteriormente a suddividere questi gruppi dittatoriali, siamo rimasti, probabilmente, con un gruppo che consiste di un singolo giudice – un dittatore. Kenneth Arrow ha dimostrato questi risultati nel 1950 anche sotto le condizioni più deboli che il sistema di voto soddisfacesse puramente la IAI e la condizione Pareto.
La Teoria di Voto
Arrow fu uno dei primi che studiò il voto da questa prospettiva matematica, cioè, come funzioni di cui si possono avere o meno certe proprietà desiderate. Il suo lavoro, comunque, ha aperto le porte a un’intera area di ricerca nella quale i matematici, gli economisti e gli scienziati politici incrociano i percorsi e condividono idee riguardo ciò che è possibile e ciò che è desiderabile.
Per esempio, Allan Gibbard nel 1973 e Mark Satterthwaite nel 1975 si sono posti il problema di determinare se un sistema di voto abbia la proprietà (apparentemente indesiderata) di poter essere manipolato. In altre parole, potrebbero esserci situazioni in cui qualcuno potrebbe ottenere un risultato più desiderabile mentendo riguardo le sue preferenze. Il lavoro di Gibbard e Satterthwaite ha portato alla conclusione che i soli sistemi di voto che erano non manipolabili avevano un dittatore unico o al massimo uno alternativo che non poteva mai vincere. I ricercatori successivi hanno considerate questioni relative a quanto spesso sia possibile una tale manipolazione e a quanto sia probabile che essa accada.
Morale
Vediamo, allora, che il ragionamento matematico, attraverso attente definizioni precise e dimostrazioni logiche, può essere applicato a situazioni oltre alla matematica e alle scienze naturali. Tale ragionamento può essere necessario per convincere se stessi di un risultato che, a prima vista, sembra controintuitivo. Nel contesto del nostro esempio olimpico, possiamo vedere che è impossibile soddisfare tutte e quattro le buone caratteristiche che vorremmo per il nostro sistema di voto, almeno quando esso è basato solo sulle classifiche dei giudici.
Non c’è bisogno di soccombere nel disperarsi, comunque. La nostra analisi sopra ci dice che dobbiamo semplicemente considerare una classe più ampia di schemi di voto nella nostra ricerca di un buon sistema. Le soluzioni degli esempi coinvolgono, in realtà, il fatto di usare i punteggi numerici prodotti da ogni giudice olimpico per qualcosa che va oltre la semplice classifica delle sue preferenze. Altre truffe includono il fatto di introdurre una piccola quantità di casualità nello schema di voto. Per esempio, talvolta, potremmo lasciar cadere, in modo casuale, punteggi di un qualche giudice, stabilendo così uno schema di voto che non è una funzione della forma che abbiamo considerato.
In effetti, quest’ ultima soluzione è stata uno degli aspetti adottati del nuovo metodo di voto per il pattinaggio di figura che è stato implementato nel 2004!
Riferimenti bibliografici
[1] W.H. Freeman & Company, For All Practical Purposes, by COMAP, 8th ed., 2008.
[2] G. Szpiro, Numbers Rule: The Vexing Mathematics of Democracy, from Plato to the Present, Princeton University Press, 2010.
[3] P. Tannebaum & R. Arnold, Excursions In Modern Mathematics, 7th edition, Prentice Hall, 2009.

