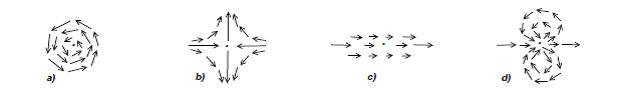Originating author is João Pimentel Nunes
The Hairy Ball Theorem is from topology, that part of mathematics that is concerned with the form of spaces. For the most part, this result came from work at the end of the 19th century by Henri Poincaré[1], considered to be one of the founders of topology.
There are few mathematical results that are so familiar to us from everyday situations: many readers are faced every morning with the hairy ball theorem when they try to comb their hair and find a persistent whorl at the top of their heads. Stated simply, the Hairy Ball Theorem says that it is impossible to comb a spherical ball covered in hair so that there are no whorls.
Check out this cool video explanation of the theorem
Our first task is to explain the terms “hair,” “comb,” and “whorl” in mathematical terms. Imagine a surface, S, in three-dimensional Euclidean space, R3. For each point p in S there is a two-dimensional plane that is tangent to S. Vectors originating from p in this plane are said to be tangent to S at p. The mathematical equivalent of “hair” are these tangent vectors. A “mathematical hairdo” on S is a choice, for each point p of S, of a tangent vector of S at p, Xp, such that these vectors vary continuously on S. That is, as two points p and q approach each other, also the vectors Xp and Xq approach each other in length and the angle between them approaches zero. Such a choice of “hairdo”, that is the collection X of the tangent vectors Xp on S, is called a continuous vector field on S. If at a given point p on S one has Xp = 0, then p is said to be a zero of X. This is equivalent to a “whorl.”
We can now state the Hairy Ball Theorem [2, 3, 4] more precisely:
“A continuous vector field on a spherical surface has at least one zero.”
The whorls associated to X are mathematically expressed by the zeros of X. For example, if X has a simple whorl around the point p, as in Figure 1a), then Xp = 0. As we approach the centre of the whorl, the vectors take all possible directions as they go around p. The only way that all of these vectors may simultaneously approach Xp , when X is continuous in p, is for the lengths of all the vectors to decrease until they go to zero at p, giving Xp = 0. The Hairy Ball Theorem therefore predicts that any continuous vector field on a spherical surface will form some kind of whorl.
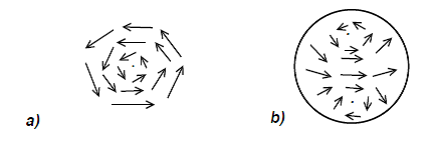
Figure 1 a) A whorl with a centre at a zero of X; b) a continuous vector field on the sphere with two whorls.
The Hairy Ball Theorem restricts the qualitative properties of the vector field X. On the other hand, for example, the vector lengths are not important. We can also check that it is valid on any surface that is topologically equivalent to a spherical surface, that is, a surface that may be obtained from it by a continuous deformation. (Imagine the spherical surface as a rubber balloon that can be deformed by hand, squeezing some regions and stretching others, but without tearing it. The surfaces thus obtained are identical to the surface of a sphere from a topological point of view.) The theorem only depends on the qualitative properties, that is, topological properties, of the surface. This is one of the hallmarks of topology, and is also one of the reasons for its wide application in many areas of mathematics: the topological information of a space is independent of some quantitative characteristics, such as area or a symmetry, for example.
We will describe an idea that explains the Hairy Ball Theorem [2, 3]. Let S be a spherical surface with center at the origin of R3, so that the point -p is antipodal to p. Let X be a continuous vector field on S. We want to show that X vanishes at some point of S. Suppose the contrary, that X never vanishes.
At each point p of S there exists a meridian in the direction of Xp because Xp does not vanish. Now imagine that each point p moves along that meridian, with equal speed for all points. After some time, the same for all points, each point p reaches its antipodal point -p. Thus, we find a family of transformations of S onto itself. At the initial instant t = 0, each point p on S transforms onto itself, so the surface undergoes the identity transformation. As t increases, each point p on S begins to move along the meridian that connects p to -p, following the direction of Xp. At the final moment, each point p arrives at its antipodal point -p. This transformation is called the antipodal transformation. Thus, we can continuously deform the identity transformation into the antipodal transformation. Now, one can show that such a deformation cannot exist, because the antipodal transformation “reverses the orientation” of S. As such a deformation does not exist, the initial assumption that X vanishes at no point of S has to be impossible, and this is exactly what the Hairy Ball Theorem states.
To explain in an informal way the meaning of “reverse orientation”, consider, by analogy, the identity transformation of R3, where each point of R3 transforms onto itself, and the transformation that takes each point p to -p. In Figure 2, we show the transformation of the initial axes on the left to the axes after the transformation p → -p.
The readers will easily convince themselves that they cannot rotate the ordered system of axes (x, y, z) to get the ordered system of axes (- x,-y,-z). This means that the transformation p → -p “reverses the orientation” of R3. What happens to the antipodal transformation of S is analogous.
The mathematical concepts underlying this heuristic explanation are homotopy and degree [2, 3]. Two transformations of S are said to be homotopic if they can be deformed continuously into one another. For example, two rotations of S may be deformed one into the other, by changing continuously the rotation angle and the axis of rotation. On the other hand, to a transformation of S into itself we can assign an integer number, its degree. The degree of the identity and the antipodal transformation are +1 and -1, respectively. The degree of a transformation of S does not change during a continuous deformation because it cannot “jump” suddenly to another integer value along a continuous deformation. Therefore, two homotopic transformations of S have the same degree, and the identity transformation and the antipodal transformation are not homotopic to each other. As we have seen, a vector field without zeros on a spherical surface would provide such homotopy and therefore this vector field cannot exist. This kind of argument, involving a discrete quantity that is invariant by continuous deformation, in this case the degree, occurs often in topology.
The Hairy Ball theorem is also a consequence of a more general theorem of Poincaré on vector fields on surfaces. Let X be a continuous vector field on a surface with an isolated zero at p, that is, such that p is the only point in its neighbourhood where X vanishes. It is possible to define the index of X at p which is an integer number, ip(X), which counts the number of times X rotates around p, as follows.
We start by identifying a small region of the surface around p with a small region of the plane. Then, we take a small circumference, C, around p, so that X is never zero along C. As we follow along C, in some chosen direction, from a given starting point, we can follow the evolution of the directions of X. When we return to the starting point, X has performed a certain whole number of complete turns. Each turn in the chosen direction counts +1 and each turn in the opposite direction counts -1. The total number of turns is the index ip(X). The reader can do this for the following examples and verify the value of the index presented:
The index, ip(X), is also a topological concept that depends only on the qualitative behavior of X near p. In fact, these ideas of Poincaré originally appeared in a text devoted to the qualitative aspects of the theory of differential equations.
Suppose now that X is a continuous vector field on a spherical surface S with isolated zeros at the points p1, p2, . . , pN. Let ![]() = ip1(X) + ip2(X) + · · · + ipN(X), be the sum of the indices of all zeros of X. It is a remarkable fact, that will definitely amaze the reader, that the integer number
= ip1(X) + ip2(X) + · · · + ipN(X), be the sum of the indices of all zeros of X. It is a remarkable fact, that will definitely amaze the reader, that the integer number ![]() does not depend on X. That is, if Y is another vector field continuous on S with zeros on q1, q2,. . . , qk, then c(Y) = iq1(Y) + iq2(Y) + · · · + iqk(Y) =
does not depend on X. That is, if Y is another vector field continuous on S with zeros on q1, q2,. . . , qk, then c(Y) = iq1(Y) + iq2(Y) + · · · + iqk(Y) = ![]() . For example, take S with a vector field with two zeros of index +1, as in Figure 1 b), one at the north pole and one at the south pole, with the sum of indices equal to +2. In another example, we may have only one zero of index +2 as in Figure 3 d). The reader may try to draw other continuous vector fields with isolated zeros on the spherical surface. The sum of the indices will always be +2. This implies the Hairy Ball theorem: if the sum of the indices of zeros of X is +2, thus not zero, then X must have zeros.
. For example, take S with a vector field with two zeros of index +1, as in Figure 1 b), one at the north pole and one at the south pole, with the sum of indices equal to +2. In another example, we may have only one zero of index +2 as in Figure 3 d). The reader may try to draw other continuous vector fields with isolated zeros on the spherical surface. The sum of the indices will always be +2. This implies the Hairy Ball theorem: if the sum of the indices of zeros of X is +2, thus not zero, then X must have zeros.
Let us explain this result. Suppose S is formed by triangles joined by the edges, so that each edge is shared by exactly two triangles. We assume that the (isolated) zeros of X and Y are inside triangles, where each triangle can contain at most one zero of X or Y. Orient the edges of each triangle so that a small ant walking along the edges on the outer side of the ball, has the interior of the triangle on its left. If an edge is shared by two neighbouring triangles T and T’, then the ant walks it in opposite directions, depending on whether it circles the triangle T or T’.
At each point p on an edge, we can measure the angle between the vectors Xp and Yp, which will vary along the edge. If this angle varies α between the beginning and end of the edge when the ant walks in one direction, then it will vary –α along the edge when it walks in the opposite direction. Thus, if we add the angle variation along all the edges of all the triangles which form S, then we obtain zero since each edge contributes twice, one time for each direction. With a little reflection, the readers can convince themselves that this zero-sum is also equal to 2π[![]() ]. In fact, if X and/or Y has a zero inside a triangle, then the total variation of the angle between X and Y along the three edges of the triangle is precisely 2π times the difference of the indices of X and Y for those zero(s). (Because the index is the number of complete turns that the vector field makes when going around a zero.) You can check that if X and Y do not have zeros inside the triangle, the total angle variation along its three edges will be zero. Incidentally, we can define ip(X) = 0 if Xp ≠ 0. Thus,
]. In fact, if X and/or Y has a zero inside a triangle, then the total variation of the angle between X and Y along the three edges of the triangle is precisely 2π times the difference of the indices of X and Y for those zero(s). (Because the index is the number of complete turns that the vector field makes when going around a zero.) You can check that if X and Y do not have zeros inside the triangle, the total angle variation along its three edges will be zero. Incidentally, we can define ip(X) = 0 if Xp ≠ 0. Thus, ![]() as stated above.
as stated above.
We conclude that, if there is a continuous vector field on a spherical surface such that the sum of the indices of its zeros is +2, then that will be true for all continuous vector fields on this surface. This, as we have seen, implies the Hairy Ball theorem.
The argument that we have described applies not only to spherical surfaces, but to all the surfaces in Figure 4, which are called orientable surfaces. Instead of the spherical surface, S can be the surface of a donut (torus) or another surface with g = 2, 3, …, where g is the number of “holes.”

Figure 4: The family of closed orientable surfaces: a) the sphere, b) a torus, c) and g = 2, d) g > 2
It is not difficult to show that if S has g holes, then the sum of the indices of the zeros of any continuous vector field on S is equal to the Euler characteristic of S, that is 2 – 2g [2, 6]. Note that ip(X) depends only on the local behaviour of X near p, whereas ![]() depends on the global shape of the surface S. In the case of the sphere, g = 0 so the sum of the indices is +2. In the case of the torus, g = 1 and the reader can easily find a continuous vector field that never vanishes. Generalising the argument slightly, one can show that this theorem of Poincaré is also valid for other surfaces that are not part of this family, such as the projective plane and the Klein bottle [2, 5].
depends on the global shape of the surface S. In the case of the sphere, g = 0 so the sum of the indices is +2. In the case of the torus, g = 1 and the reader can easily find a continuous vector field that never vanishes. Generalising the argument slightly, one can show that this theorem of Poincaré is also valid for other surfaces that are not part of this family, such as the projective plane and the Klein bottle [2, 5].
Later, in 1926, the German mathematician Heinz Hopf [7] generalised the theorem of Poincaré for surfaces to geometric objects of dimension greater than two. These results illustrate the modus operandi of topology, which was strongly developed over the twentieth century. It applies with great power in many areas of mathematics including geometry, analysis, dynamical systems and differential equations, characterising the qualitative and global aspects of the problems in question.
We can model the horizontal component of the velocity of the air in the atmosphere at a certain altitude by a continuous vector field on the surface of a sphere. The Hairy Ball theorem predicts, then, the existence of zeros, as well as the resulting eddies such as cyclones, in the movement of the atmosphere. Likewise, it applies to the movement of ultra-hot gases in the atmosphere of the Sun, which constantly form impressive whorls. Part of the beauty of the language of mathematics comes from the unifying description of phenomena as diverse as our morning hairstyle and the Sun’s atmosphere, through the same set of concepts that can be applied with great efficiency both in the description of the physical world or in the most abstract problems.
References
[1] http://pt.wikipedia.org/wiki/Henri_Poincaré, http://www.poincare.fr
[2] W. Fulton, Algebraic Topology – a first course, Springer-Verlag 1995.
[3] E.L. Lima, Curso de Analise, Vol.2, Chapter VII, Projecto Euclides, IMPA, 1981.
[4] http://en.wikipedia.org/wiki/Hairy_ball_theorem
[5] http://en.wikipedia.org/wiki/Real_projective_plane, http://en.wikipedia.org/wiki/Klein_bottle
[6] http://en.wikipedia.org/wiki/Euler_characteristic
[7] http://en.wikipedia.org/wiki/Heinz_Hopf