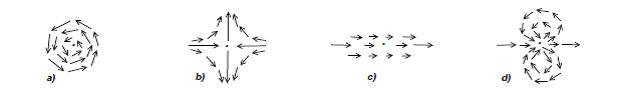Autor do original: João Pimentel Nunes.
O teorema da bola cabeluda é um resultado da Topologia, a disciplina matemática que estuda a forma dos espaços. Em grande parte, ele resulta do trabalho nos finais do século XIX do grande matemático francês Henri Poincaré [1], considerado um dos fundadores da Topologia.
Haverá poucos resultados matemáticos que nos sejam tão familiares dos gestos do quotidiano: muitos dos leitores confrontam-se todas as manhãs com o teorema da bola cabeluda, ao tentarem pentear o seu cabelo e verificando que há um remoínho persistente no topo das suas cabeças. De um modo simplificado, o teorema afirma que não é possível “pentear-se” uma superfície esférica coberta de “cabelo” sem se formarem “remoínhos” de algum tipo.
A nossa primeira tarefa é explicar o que significa “cabelo”, “pentear” e “remoínho” em termos matemáticos. Imaginemos uma superfície, ![]() , no espaço euclidiano tridimensional
, no espaço euclidiano tridimensional ![]() . Por cada ponto
. Por cada ponto ![]() de
de ![]() passa um plano bidimensional tangente a
passa um plano bidimensional tangente a ![]() . Os vectores com origem em p e assentes nesse plano dizem-se vectores tangentes a S em p. O “cabelo” matemático é formado por tais vectores tangentes. Um “penteado” matemático de
. Os vectores com origem em p e assentes nesse plano dizem-se vectores tangentes a S em p. O “cabelo” matemático é formado por tais vectores tangentes. Um “penteado” matemático de ![]() consiste numa escolha, para cada ponto
consiste numa escolha, para cada ponto ![]() de
de ![]() , de um vector tangente a
, de um vector tangente a ![]() em
em ![]() ,
, ![]() , de modo a que esses vectores variem continuamente sobre
, de modo a que esses vectores variem continuamente sobre ![]() . Ou seja, á medida que dois pontos de
. Ou seja, á medida que dois pontos de ![]() ,
, ![]() e
e ![]() , se aproximam um do outro, também os vectores
, se aproximam um do outro, também os vectores ![]() e
e ![]() se aproximam no sentido que os seus comprimentos vão ficando iguais e que o ângulo entre eles vai ficando cada vez mais próximo de zero. A uma tal coleção,
se aproximam no sentido que os seus comprimentos vão ficando iguais e que o ângulo entre eles vai ficando cada vez mais próximo de zero. A uma tal coleção, ![]() , de vectores tangentes a
, de vectores tangentes a ![]() chama-se um campo vectorial contínuo em S. Se para um dado ponto
chama-se um campo vectorial contínuo em S. Se para um dado ponto ![]() de
de ![]() se tem
se tem ![]() , então diz-se que p é um zero de X. Podemos agora enunciar o teorema da bola cabeluda [2, 3, 4] de forma mais precisa:
, então diz-se que p é um zero de X. Podemos agora enunciar o teorema da bola cabeluda [2, 3, 4] de forma mais precisa:
“Um campo vectorial contínuo na superfície esférica tem pelo menos um zero.”
Os remoínhos que ![]() forma expressam-se matematicamente através dos zeros de
forma expressam-se matematicamente através dos zeros de ![]() . Por exemplo, se
. Por exemplo, se ![]() forma um remoínho simples em torno do ponto
forma um remoínho simples em torno do ponto ![]() , como na Figura 1 a), então
, como na Figura 1 a), então ![]() . De facto, quando nos aproximamos do centro do remoínho, os vectores vão tomando todas as possíveis direcções medida que rodamos à volta de
. De facto, quando nos aproximamos do centro do remoínho, os vectores vão tomando todas as possíveis direcções medida que rodamos à volta de ![]() . A única forma de estes vectores se aproximarem todos ao mesmo tempo do vector
. A única forma de estes vectores se aproximarem todos ao mesmo tempo do vector ![]() , o que é exigido para que
, o que é exigido para que ![]() seja contínuo em
seja contínuo em ![]() , é então que os comprimentos vão diminuindo até se anularem em
, é então que os comprimentos vão diminuindo até se anularem em ![]() , obtendo-se
, obtendo-se ![]() . O teorema da bola cabeluda prevê, portanto, que qualquer campo vectorial contínuo na superfície esférica forme algum tipo de remoínho.
. O teorema da bola cabeluda prevê, portanto, que qualquer campo vectorial contínuo na superfície esférica forme algum tipo de remoínho.
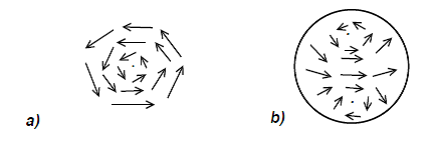
Figura 1: a) Um remoínho, com um zero de X no centro. b) Um campo vectorial contínuo na esfera,com dois remoínhos.
O teorema da bola cabeluda restringe as características qualitativas do campo vectorial ![]() . Por outro lado, por exemplo, a ordem de grandeza do comprimento dos vectores não é importante. Pode ainda verificar-se que ele é válido em qualquer superfície que seja topologicamente equivalente a uma superfície esférica, por exemplo, que possa ser obtida dela por uma deforma¸cão contínua. (Imaginemos que a superfície esférica é um balão de borracha que podemos deformar com as mãos, apertando-o numas regiões e esticando-o noutras, mas sem o romper. As superfícies assim obtidas são idênticas à superfície esférica, do ponto de vista topológico.) O teorema só depende das características qualitativas, ou seja topológicas, da superfície. Esta é uma das marcas da Topologia, e também uma das razões da sua vasta aplicação em tantas áreas da Matemática: a informação topológica de um espaço é independente de algumas características quantitativas, como a área ou a simetria no caso de uma superfície, por exemplo.
. Por outro lado, por exemplo, a ordem de grandeza do comprimento dos vectores não é importante. Pode ainda verificar-se que ele é válido em qualquer superfície que seja topologicamente equivalente a uma superfície esférica, por exemplo, que possa ser obtida dela por uma deforma¸cão contínua. (Imaginemos que a superfície esférica é um balão de borracha que podemos deformar com as mãos, apertando-o numas regiões e esticando-o noutras, mas sem o romper. As superfícies assim obtidas são idênticas à superfície esférica, do ponto de vista topológico.) O teorema só depende das características qualitativas, ou seja topológicas, da superfície. Esta é uma das marcas da Topologia, e também uma das razões da sua vasta aplicação em tantas áreas da Matemática: a informação topológica de um espaço é independente de algumas características quantitativas, como a área ou a simetria no caso de uma superfície, por exemplo.
Vamos descrever uma ideia que explica o teorema da bola cabeluda [2, 3]. Seja S uma superfície esférica em ![]() com centro na origem, de modo a que
com centro na origem, de modo a que ![]() seja o ponto antípoda de
seja o ponto antípoda de ![]() . Seja
. Seja ![]() um campo vectorial contínuo em S. Queremos mostrar que
um campo vectorial contínuo em S. Queremos mostrar que ![]() se anula nalgum ponto de S. Suponhamos o contrário, ou seja, que
se anula nalgum ponto de S. Suponhamos o contrário, ou seja, que ![]() nunca se anula. Então, em cada ponto
nunca se anula. Então, em cada ponto ![]() de
de ![]() passa um meridiano com a direcção de
passa um meridiano com a direcção de ![]() , porque
, porque ![]() não se anula. Imaginemos agora que cada ponto
não se anula. Imaginemos agora que cada ponto ![]() se desloca ao longo desse meridiano, com velocidade igual para todos os pontos. Após algum tempo, igual para todos os pontos, cada ponto
se desloca ao longo desse meridiano, com velocidade igual para todos os pontos. Após algum tempo, igual para todos os pontos, cada ponto ![]() chegou ao seu antípoda
chegou ao seu antípoda ![]() . Deste modo, encontramos uma fam´ılia de transforma¸cões de S em si própria: no instante
. Deste modo, encontramos uma fam´ılia de transforma¸cões de S em si própria: no instante ![]() , cada ponto
, cada ponto ![]() de
de ![]() transforma-se nele próprio, ou seja, temos a transformação identidade; à medida que
transforma-se nele próprio, ou seja, temos a transformação identidade; à medida que ![]() aumenta, cada ponto
aumenta, cada ponto ![]() de
de ![]() come ça a deslocar-se ao longo do meridiano que o liga a
come ça a deslocar-se ao longo do meridiano que o liga a ![]() , seguindo a direcção de
, seguindo a direcção de ![]() . No instante final, cada ponto
. No instante final, cada ponto ![]() chegou finalmente ao seu antípoda
chegou finalmente ao seu antípoda ![]() , e esta transformação chama-se a transformação antipodal. Deste modo, deformamos continuamente a transformação identidade na transformação antipodal. Ora, pode mostrar-se que tal deformação não pode existir, porque a transformaçãao antipodal “inverte a orientação” de
, e esta transformação chama-se a transformação antipodal. Deste modo, deformamos continuamente a transformação identidade na transformação antipodal. Ora, pode mostrar-se que tal deformação não pode existir, porque a transformaçãao antipodal “inverte a orientação” de ![]() . Como tal deformação não existe, a suposição inicial de que
. Como tal deformação não existe, a suposição inicial de que ![]() não se anulava em nenhum ponto tem de ser impossível, e é isso mesmo que afirma o teorema da bola cabeluda.
não se anulava em nenhum ponto tem de ser impossível, e é isso mesmo que afirma o teorema da bola cabeluda.
Um modo informal de explicar o que significa “inverter a orientação”, é considerar, por analogia, a transforma¸cão identidade de ![]() , em que cada ponto de
, em que cada ponto de ![]() é transformado em si próprio, e a transformação que leva cada ponto
é transformado em si próprio, e a transformação que leva cada ponto ![]() para
para ![]() . Na Figura 2, temos à esquerda uma escolha inicial de eixos e à direita representam-se esses eixos após a transformação
. Na Figura 2, temos à esquerda uma escolha inicial de eixos e à direita representam-se esses eixos após a transformação ![]() .
.
O leitor facilmente se convence que n˜ao consegue rodar o sistema ordenado de eixos ![]() até obter o sistema ordenado de eixos
até obter o sistema ordenado de eixos ![]() . Isto significa que a transforma¸cãao
. Isto significa que a transforma¸cãao ![]() “inverte a orientação” de
“inverte a orientação” de ![]() . O que acontece com a transformação antipodal de S é análogo.
. O que acontece com a transformação antipodal de S é análogo.
Os conceitos matemáticos na base desta explicação heurística são a homotopia e o grau [2, 3]. Duas transformações de ![]() dizem-se homotópicas se se podem deformar continuamente uma na outra. Por exemplo, duas rotações de
dizem-se homotópicas se se podem deformar continuamente uma na outra. Por exemplo, duas rotações de ![]() podem deformar-se uma na outra, mudando-se continuamente o eixo e o ângulo de rotação. Por outro lado, a uma transformação de
podem deformar-se uma na outra, mudando-se continuamente o eixo e o ângulo de rotação. Por outro lado, a uma transformação de ![]() nela própria podemos atribuir um número inteiro, o seu grau. O grau da identidade
nela própria podemos atribuir um número inteiro, o seu grau. O grau da identidade ![]() e o da transformação antipodal
e o da transformação antipodal ![]() . Ao deformamos uma transformação de
. Ao deformamos uma transformação de ![]() o grau não se altera, pois ele não pode “saltar” repentinamente para outro valor inteiro ao longo de uma deformação contínua. Logo, duas transformações homotópicas de
o grau não se altera, pois ele não pode “saltar” repentinamente para outro valor inteiro ao longo de uma deformação contínua. Logo, duas transformações homotópicas de ![]() têm o mesmo grau, e a transformação identidade e a transformação antipodal não são homotópicas entre si. Como vimos, um campo vectorial contínuo sem zeros na superfície esférica forneceria essa homotopia e, portanto, esse campo vectorial não pode existir. Este tipo de argumento, envolvendo uma grandeza discreta que é invariante por deforma¸cão contínua, neste caso o grau, é frequente em Topologia.
têm o mesmo grau, e a transformação identidade e a transformação antipodal não são homotópicas entre si. Como vimos, um campo vectorial contínuo sem zeros na superfície esférica forneceria essa homotopia e, portanto, esse campo vectorial não pode existir. Este tipo de argumento, envolvendo uma grandeza discreta que é invariante por deforma¸cão contínua, neste caso o grau, é frequente em Topologia.
O teorema da bola cabeluda é também consequência de um teorema mais geral de Poincaré sobre campos vectoriais em superfícies. Seja ![]() um campo vectorial contínuo numa superfície, com um zero isolado em
um campo vectorial contínuo numa superfície, com um zero isolado em ![]() , ou seja tal que
, ou seja tal que ![]() é o único ponto na sua vizinhança onde
é o único ponto na sua vizinhança onde ![]() se anula. É possível definir-se o índice de
se anula. É possível definir-se o índice de ![]() em
em ![]() que é um número inteiro,
que é um número inteiro, ![]() , que conta o número de vezes que
, que conta o número de vezes que ![]() “roda” em torno de
“roda” em torno de ![]() , do modo seguinte: Começamos por planificar uma pequena região da superfície à volta de
, do modo seguinte: Começamos por planificar uma pequena região da superfície à volta de ![]() , ou seja, identificamo-la com uma pequena região do plano. Em seguida, tomamos uma circunferência,
, ou seja, identificamo-la com uma pequena região do plano. Em seguida, tomamos uma circunferência, ![]() , à volta de
, à volta de ![]() e orientada num sentido à escolha, de modo a que
e orientada num sentido à escolha, de modo a que ![]() não se anule ao longo de
não se anule ao longo de ![]() . Ao seguirmos ao longo de
. Ao seguirmos ao longo de ![]() no sentido escolhido, a partir de um dado ponto inicial, podemos ir seguindo a evolução da direcção de
no sentido escolhido, a partir de um dado ponto inicial, podemos ir seguindo a evolução da direcção de ![]() . Quando regressamos ao ponto inicial,
. Quando regressamos ao ponto inicial, ![]() deu um certo número inteiro de voltas completas. Cada volta no sentido de
deu um certo número inteiro de voltas completas. Cada volta no sentido de ![]() conta +1 e cada volta no sentido inverso conta −1. O número total de voltas é o índice
conta +1 e cada volta no sentido inverso conta −1. O número total de voltas é o índice ![]() . O leitor pode fazer este exercício nos exemplos seguintes e verificar o valor do índice apresentado:
. O leitor pode fazer este exercício nos exemplos seguintes e verificar o valor do índice apresentado:
O índice, ![]() , é também um conceito “topológico” que depende apenas do comportamento qualitativo de
, é também um conceito “topológico” que depende apenas do comportamento qualitativo de ![]() perto de
perto de ![]() . Na verdade, estas ideias de Poincaré apareceram originalmente num texto dedicado a aspectos
. Na verdade, estas ideias de Poincaré apareceram originalmente num texto dedicado a aspectos ![]() da teoria das equa¸cões diferenciais.
da teoria das equa¸cões diferenciais.
Suponhamos agora que ![]() é um campo vectorial contínuo na superfície esférica
é um campo vectorial contínuo na superfície esférica ![]() , com zeros isolados, nos pontos
, com zeros isolados, nos pontos ![]() Seja
Seja ![]() , a soma dos índices de todos os zeros de X. ´E um facto not´avel, que vai certamente maravilhar o leitor, que
, a soma dos índices de todos os zeros de X. ´E um facto not´avel, que vai certamente maravilhar o leitor, que ![]() é um inteiro que não depende de X. Ou seja, se Y for outro campo vectorial contínuo em
é um inteiro que não depende de X. Ou seja, se Y for outro campo vectorial contínuo em ![]() , com zeros em
, com zeros em ![]() então
então ![]() . Por exemplo, em
. Por exemplo, em ![]() podemos ter um campo vectorial com dois zeros de índice +1, como na Figura 1 b), um no pólo Norte e outro no pólo Sul, com soma dos índices igual a +2. Noutro exemplo, podemos ter apenas um zero de índice +2 como o da Figura 3 d). O leitor pode experimentar desenhar outros campos vectoriais contínuos, com zeros isolados, na superfície esférica; a soma dos índices ser´a sempre +2! Isto implica o teorema da bola cabeluda: se a soma dos índices dos zeros de X ´e +2, e portanto não é nula, então
podemos ter um campo vectorial com dois zeros de índice +1, como na Figura 1 b), um no pólo Norte e outro no pólo Sul, com soma dos índices igual a +2. Noutro exemplo, podemos ter apenas um zero de índice +2 como o da Figura 3 d). O leitor pode experimentar desenhar outros campos vectoriais contínuos, com zeros isolados, na superfície esférica; a soma dos índices ser´a sempre +2! Isto implica o teorema da bola cabeluda: se a soma dos índices dos zeros de X ´e +2, e portanto não é nula, então ![]() tem de ter zeros.
tem de ter zeros.
Expliquemos como chegar a este resultado. Suponhamos que S é formada por triângulos colados uns aos outros pelas arestas, de modo a que cada aresta seja partilhada por exactamente dois triângulos. Assumimos que os zeros (isolados) de ![]() e de
e de ![]() estão no interior de triângulos, podendo cada triângulo conter no máximo um zero de
estão no interior de triângulos, podendo cada triângulo conter no máximo um zero de ![]() ou de
ou de ![]() . Orientamos as arestas de cada triângulo de modo a que uma pequena formiga passeando-se ao longo das arestas, do lado exterior da esfera, tenha o interior do triângulo à sua esquerda. Se uma aresta é partilhada por dois triângulos vizinhos
. Orientamos as arestas de cada triângulo de modo a que uma pequena formiga passeando-se ao longo das arestas, do lado exterior da esfera, tenha o interior do triângulo à sua esquerda. Se uma aresta é partilhada por dois triângulos vizinhos ![]() e
e ![]() 0, então ela é percorrida em sentidos opostos pela formiga, consoante esta esteja a rodear o triângulo
0, então ela é percorrida em sentidos opostos pela formiga, consoante esta esteja a rodear o triângulo ![]() ou
ou ![]() 0.
0.
Em cada ponto ![]() de uma aresta podemos medir o ângulo entre os vectores
de uma aresta podemos medir o ângulo entre os vectores ![]() e
e ![]() , que irá variando ao longo da aresta. Se esse ângulo varia entre o in´ıcio e o fim da aresta quando ela é percorrida num sentido, então ele vai variar − se a aresta é percorrida no sentido oposto. Logo, se somarmos a variação do ângulo ao longo de todas as arestas de todos os triângulos que formam S, obtemos zero porque cada aresta contribui duas vezes, sendo percorrida uma vez em cada sentido. Ora, com um pouco de reflexão, o leitor pode convencer-se de que esta soma nula é também igual a
, que irá variando ao longo da aresta. Se esse ângulo varia entre o in´ıcio e o fim da aresta quando ela é percorrida num sentido, então ele vai variar − se a aresta é percorrida no sentido oposto. Logo, se somarmos a variação do ângulo ao longo de todas as arestas de todos os triângulos que formam S, obtemos zero porque cada aresta contribui duas vezes, sendo percorrida uma vez em cada sentido. Ora, com um pouco de reflexão, o leitor pode convencer-se de que esta soma nula é também igual a ![]() . De facto, se
. De facto, se ![]() e/ou
e/ou ![]() têm um zero no interior de um triângulo, então a varia¸cão total do ângulo entre
têm um zero no interior de um triângulo, então a varia¸cão total do ângulo entre ![]() e
e ![]() ao longo das três arestas desse triângulo é precisamente
ao longo das três arestas desse triângulo é precisamente ![]() vezes a diferença dos índices de
vezes a diferença dos índices de ![]() e de
e de ![]() nesse(s) zero(s). (Porque o índice é o número de voltas completas que o campo vectorial dá quando rodamos à volta de um zero.) Pode verificar-se que se
nesse(s) zero(s). (Porque o índice é o número de voltas completas que o campo vectorial dá quando rodamos à volta de um zero.) Pode verificar-se que se ![]() e
e ![]() não tiverem zeros no interior do triângulo, a variação total do ângulo ao longo das três arestas desse triângulo será zero. Aliás, pode mesmo definir-se
não tiverem zeros no interior do triângulo, a variação total do ângulo ao longo das três arestas desse triângulo será zero. Aliás, pode mesmo definir-se ![]() se
se ![]() . Portanto,
. Portanto, ![]() como foi afirmado acima.
como foi afirmado acima.
Conclui-se que, se houver um campo vectorial contínuo na superfície esférica tal que a soma dos índices dos seus zeros seja +2, então isso será verdade para todos os campos vectoriais contínuos nessa superfície. Isto, como vimos, implica o teorema da bola cabeluda.
O argumento que descrevemos aplica-se não apenas à superfície esférica, mas a todas as superfícies da Figura 4, que são chamadas superfícies orientáveis. Em vez da superfície esférica, ![]() pode ser a superfície de um donut (o
pode ser a superfície de um donut (o ![]() ), ou outra superfície com g = 2, 3, … “buracos”.
), ou outra superfície com g = 2, 3, … “buracos”.

Figura 4: A família das superfícies fechadas orientáveis: a) a esfera, b) o toro, c) g = 2, d) g > 2
Não é difícil mostrar que se ![]() tem
tem ![]() buracos, então a soma dos índices dos zeros de qualquer campo vectorial contínuo em
buracos, então a soma dos índices dos zeros de qualquer campo vectorial contínuo em ![]() é igual à característica de Euler de S, que vale 2 − 2g [2, 6]. Notemos que
é igual à característica de Euler de S, que vale 2 − 2g [2, 6]. Notemos que ![]() depende apenas do comportamento local de
depende apenas do comportamento local de ![]() perto de
perto de ![]() , ao passo que
, ao passo que ![]() depende da forma global da superfície
depende da forma global da superfície ![]() . No caso da esfera,
. No caso da esfera, ![]() e obtemos que a soma dos índices é +2. No caso do toro, g = 1 e o leitor facilmente encontra um campo vectorial contínuo que nunca se anula. Generalizando um pouco o argumento, mostra-se que este teorema de Poincaré é também válido para outras superfícies que não fazem parte desta família, como o plano projectivo e a garrafa de Klein [2, 5].
e obtemos que a soma dos índices é +2. No caso do toro, g = 1 e o leitor facilmente encontra um campo vectorial contínuo que nunca se anula. Generalizando um pouco o argumento, mostra-se que este teorema de Poincaré é também válido para outras superfícies que não fazem parte desta família, como o plano projectivo e a garrafa de Klein [2, 5].
Mais tarde, em 1926, o matemático alemão Heinz Hopf [7], generalizou o teorema de Poincaré de superfícies para objectos geométricos de dimensão superior a dois. Estes resultados ilustram o modus operandi da Topologia, que foi fortemente desenvolvida ao longo do século XX. Ela aplica-se, com grande poder, em muitas áreas da Matemática incluindo a Geometria, a Análise, os Sistemas Dinâmicos e as Equações Diferenciais, caracterizando os aspectos qualitativos e globais dos problemas em questão.
Podemos modelar a componente horizontal da velocidade do ar atmosférico, a uma determinada altitude, por um campo vectorial contínuo na superfície de uma esfera. O teorema da bola cabeluda prevê, então, a existência de zeros, e também dos consequentes remoínhos, como os ciclones, nos movimentos da atmosfera. Igualmente, ele aplica-se ao movimento dos gases ultra-quentes da atmosfera do Sol, que constantemente formam remoínhos impressionantes. Parte da beleza da linguagem matemática vem de ela unificar a descrição de fenómenos tão diversos, como o nosso penteado matinal e a atmosfera do Sol, através do mesmo conjunto de conceitos, que podem ser aplicados com uma eficácia enorme quer na descrição do mundo físico quer nos problemas mais abstractos.
Referências
[1] http://pt.wikipedia.org/wiki/Henri Poincaré, http://www.poincare.fr
[2] W.Fulton, “Algebraic Topology – a first course”, Springer-Verlag 1995.
[3] E.L.Lima, Capítulo VII, “Curso de An´alise, Vol.2”, Projecto Euclides, IMPA, 1981.
[4] http://en.wikipedia.org/wiki/Hairy ball theorem
[5] http://en.wikipedia.org/wiki/Real projective plane,
http://en.wikipedia.org/wiki/Klein bottle
[6] http://en.wikipedia.org/wiki/Euler characteristic
[7] http://en.wikipedia.org/wiki/Heinz Hopf