Autor: João Pimentel Nunes
Übersetzt von Anna Muff (Universität Würzburg)
Der Satz vom Igel (The Hairy Ball Theorem) ist ein Satz aus der Topologie, dem Teilgebiet der Mathematik, das sich mit der Form von Räumen befasst. Im Wesentlichen hat Henri Poincaré, der als einer der Begründer der Topologie angesehen wird, dieses Ergebnis am Ende des 19. Jahrhunderts gefunden [1].
Es gibt einige mathematische Resultate, die uns aus Alltagssituationen bekannt sind: So werden viele von uns jeden Morgen mit dem Satz vom Igel konfrontiert, wenn sie versuchen ihre Haare zu kämmen und dabei einen hartnäckigen Wirbel auf ihrem Kopf vorfinden. Um es einfach auszudrücken besagt der Satz vom Igel, dass es unmöglich ist eine behaarte sphärische Kugel so zu kämmen, dass keine Wirbel entstehen.
Dieses Video erklärt den Satz auf wirklich nette Weise.
Unsere erste Aufgabe ist es nun, die Begriffe „Haar“, „kämmen“ und „Wirbel“ mathematisch zu erklären. Man stelle sich eine Fläche ![]() im dreidimensionalen euklidischen Raum
im dreidimensionalen euklidischen Raum ![]() vor. Zu jedem Punkt
vor. Zu jedem Punkt ![]() auf
auf ![]() existiert eine zweidimensionale Ebene, die tangential zu
existiert eine zweidimensionale Ebene, die tangential zu ![]() ist. Vektoren, die von
ist. Vektoren, die von ![]() in dieser Ebene ausgehen, heißen tangential zu
in dieser Ebene ausgehen, heißen tangential zu ![]() in
in ![]() . Das mathematische Pendant zu „Haar“ sind eben diese Vektoren. Eine „mathematische Frisur“ auf
. Das mathematische Pendant zu „Haar“ sind eben diese Vektoren. Eine „mathematische Frisur“ auf ![]() ist die Wahl, für jeden Punkt
ist die Wahl, für jeden Punkt ![]() in
in ![]() , eines tangentialen Vektors von
, eines tangentialen Vektors von ![]() in
in ![]() ,
, ![]() , so dass sich diese Vektoren stetig auf
, so dass sich diese Vektoren stetig auf ![]() verändern. Das bedeutet, dass sich bei einer Annäherung von zwei Punkten
verändern. Das bedeutet, dass sich bei einer Annäherung von zwei Punkten ![]() und
und ![]() , auch die Längen der Vektoren
, auch die Längen der Vektoren ![]() und
und ![]() annähern und der Winkel zwischen ihnen gegen null strebt. Eine solche Wahl der „Frisur“, also die Zusammenfassung
annähern und der Winkel zwischen ihnen gegen null strebt. Eine solche Wahl der „Frisur“, also die Zusammenfassung ![]() der tangentialen Vektoren
der tangentialen Vektoren ![]() auf
auf ![]() , nennt man stetiges Vektorfeld auf
, nennt man stetiges Vektorfeld auf ![]() . Wenn in einem festen Punkt
. Wenn in einem festen Punkt ![]() auf
auf ![]() nun
nun ![]() ist, dann heißt
ist, dann heißt ![]() Nullstelle von
Nullstelle von ![]() . Dies entspricht einem „Wirbel“.
. Dies entspricht einem „Wirbel“.
Nun kann der Satz vom Igel [2, 3, 4] präziser angegeben werden:
„Jedes glatte Vektorfeld auf einer Sphäre hat wenigstens eine Nullstelle.“
Die zu ![]() gehörigen Wirbel werden mathematisch durch die Nullstellen von
gehörigen Wirbel werden mathematisch durch die Nullstellen von ![]() ausgedrückt. Wenn
ausgedrückt. Wenn ![]() beispielsweise einen einfachen Wirbel um den Punkt
beispielsweise einen einfachen Wirbel um den Punkt ![]() hat, wie in Abbildung 1a), dann ist
hat, wie in Abbildung 1a), dann ist ![]() . Wenn man sich dem Zentrum des Wirbels immer weiter nähert, nehmen die Vektoren alle möglichen Richtungen an, während sie um p gehen. Die einzige Möglichkeit, dass sich alle diese Vektoren gleichzeitig
. Wenn man sich dem Zentrum des Wirbels immer weiter nähert, nehmen die Vektoren alle möglichen Richtungen an, während sie um p gehen. Die einzige Möglichkeit, dass sich alle diese Vektoren gleichzeitig ![]() nähern, wenn
nähern, wenn ![]() stetig in
stetig in ![]() ist, ist, dass sich die Längen aller Vektoren verringern bis sie in
ist, ist, dass sich die Längen aller Vektoren verringern bis sie in ![]() gegen null gehen, so dass
gegen null gehen, so dass ![]() . Der Satz vom Igel sagt also voraus, dass jedes glatte Vektorfeld auf einer Sphäre irgendeine Art von Wirbel erzeugen wird.
. Der Satz vom Igel sagt also voraus, dass jedes glatte Vektorfeld auf einer Sphäre irgendeine Art von Wirbel erzeugen wird.
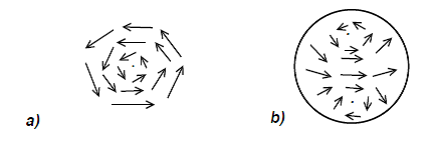
Abbildung 1 a) Ein Wirbel mit einem Zentrum bei einer Nullstelle von X
b) ein stetiges Vektorfeld auf der Sphäre mit zwei Wirbeln
Der Satz vom Igel schränkt die qualitativen Eigenschaften des Vektorfeldes ![]() ein. Auf der anderen Seite ist beispielsweise die Länge der Vektoren unwichtig. Man kann auch prüfen, dass das für jede Fläche gilt, die topologisch äquivalent zu einer Sphäre ist, das bedeutet, eine Fläche, die man daraus durch eine stetige Umformung erhält. (Man stelle sich diese Sphäre als Luftballon vor, der mit den Händen verformt werden kann, indem man eine Stelle zusammendrückt und eine andere auseinanderzieht, ohne ihn zu zerreißen. Die Flächen, die so entstehen sind identisch mit der Fläche einer Sphäre aus topologischer Sicht.) Der Satz hängt nur von den qualitativen Eigenschaften, das heißt von den topologischen Eigenschaften, ab. Dies ist eines der Kennzeichen der Topologie und es ist auch einer der Gründe für seine umfangreiche Anwendung in vielen Gebieten der Mathematik: die topologische Information eines Raumes ist unabhängig von einigen quantitativen Charakteristiken, wie zum Beispiel Flächeninhalt oder Symmetrie.
ein. Auf der anderen Seite ist beispielsweise die Länge der Vektoren unwichtig. Man kann auch prüfen, dass das für jede Fläche gilt, die topologisch äquivalent zu einer Sphäre ist, das bedeutet, eine Fläche, die man daraus durch eine stetige Umformung erhält. (Man stelle sich diese Sphäre als Luftballon vor, der mit den Händen verformt werden kann, indem man eine Stelle zusammendrückt und eine andere auseinanderzieht, ohne ihn zu zerreißen. Die Flächen, die so entstehen sind identisch mit der Fläche einer Sphäre aus topologischer Sicht.) Der Satz hängt nur von den qualitativen Eigenschaften, das heißt von den topologischen Eigenschaften, ab. Dies ist eines der Kennzeichen der Topologie und es ist auch einer der Gründe für seine umfangreiche Anwendung in vielen Gebieten der Mathematik: die topologische Information eines Raumes ist unabhängig von einigen quantitativen Charakteristiken, wie zum Beispiel Flächeninhalt oder Symmetrie.
Wir werden eine Idee beschreiben, die den Satz vom Igel erklärt [2, 3]. Sei ![]() eine Sphäre mit Zentrum im Ursprung von
eine Sphäre mit Zentrum im Ursprung von ![]() , so dass der Punkt
, so dass der Punkt ![]() antipodisch zu
antipodisch zu ![]() ist. Sei
ist. Sei ![]() ein glattes Vektorfeld auf
ein glattes Vektorfeld auf ![]() . Wir wollen zeigen, dass
. Wir wollen zeigen, dass ![]() an einem Punkt von
an einem Punkt von ![]() verschwindet. Wir nehmen nun an, es passiert das Gegenteil, nämlich dass
verschwindet. Wir nehmen nun an, es passiert das Gegenteil, nämlich dass ![]() nirgends verschwindet.
nirgends verschwindet.
An jedem Punkt ![]() auf
auf ![]() gibt es einen Meridian in die Richtung
gibt es einen Meridian in die Richtung ![]() , da
, da ![]() nicht verschwindet.
nicht verschwindet.
Stellen wir uns nun vor, dass sich jeder Punkt ![]() entlang dieses Meridians bewegt, mit gleicher Geschwindigkeit für alle Punkte. Nach einiger Zeit, dies gilt gleichermaßen für alle Punkte, wird jeder Punkt
entlang dieses Meridians bewegt, mit gleicher Geschwindigkeit für alle Punkte. Nach einiger Zeit, dies gilt gleichermaßen für alle Punkte, wird jeder Punkt ![]() seinen antipodischen Punkt
seinen antipodischen Punkt ![]() erreichen. Daher findet man eine Familie von Transformationen von
erreichen. Daher findet man eine Familie von Transformationen von ![]() auf sich selbst. Am Anfangszeitpunkt
auf sich selbst. Am Anfangszeitpunkt ![]() transformiert sich jeder Punkt
transformiert sich jeder Punkt ![]() auf
auf ![]() auf sich selbst, die Fläche erfährt also eine Identitätstransformation. Mit steigendem
auf sich selbst, die Fläche erfährt also eine Identitätstransformation. Mit steigendem ![]() bewegt sich jeder Punkt
bewegt sich jeder Punkt ![]() auf
auf ![]() entlang des Meridian, der
entlang des Meridian, der ![]() und
und ![]() verbindet, in der Richtung
verbindet, in der Richtung ![]() . Zum letzten Zeitpunkt kommt jeder Punkt
. Zum letzten Zeitpunkt kommt jeder Punkt ![]() an seinem antipodischen Punkt
an seinem antipodischen Punkt ![]() an. Diese Transformation wird antipodische Transformation genannt. Auf diese Weise kann man kontinuierlich die Identitätstransformation zu einer antipodischen Transformation verformen. Nun kann man zeigen, dass eine solche Deformation nicht existiert, da die antipodische Transformation die „Orientierung von
an. Diese Transformation wird antipodische Transformation genannt. Auf diese Weise kann man kontinuierlich die Identitätstransformation zu einer antipodischen Transformation verformen. Nun kann man zeigen, dass eine solche Deformation nicht existiert, da die antipodische Transformation die „Orientierung von ![]() umkehrt“. Da eine solche Deformation nicht existiert, muss die anfängliche Annahme, dass
umkehrt“. Da eine solche Deformation nicht existiert, muss die anfängliche Annahme, dass ![]() in keinem Punkt von
in keinem Punkt von ![]() verschwindet, unmöglich sein. Das ist genau die Aussage des Satzes vom Igel.
verschwindet, unmöglich sein. Das ist genau die Aussage des Satzes vom Igel.
Um die Bedeutung von „umgekehrter Orientierung“ auf informelle Weise zu erklären, betrachte man in Analogie dazu die Identitätstransformation von ![]() , wo jeder Punkt im
, wo jeder Punkt im ![]() auf sich selbst transformiert wird und die Transformation, die jeden Punkt
auf sich selbst transformiert wird und die Transformation, die jeden Punkt ![]() zu
zu ![]() bringt. In Abbildung 2 wird die Transformation der Anfangsachsen links zu den Achsen nach der Transformation
bringt. In Abbildung 2 wird die Transformation der Anfangsachsen links zu den Achsen nach der Transformation ![]() gezeigt.
gezeigt.
Die Leser können sich leicht davon überzeugen, dass man das angeordnete System der Achsen ![]() nicht drehen kann, so dass man das angeordnete System der Achsen
nicht drehen kann, so dass man das angeordnete System der Achsen ![]() erhält. Das bedeutet, dass die Transformation
erhält. Das bedeutet, dass die Transformation ![]() die „Orientierung von
die „Orientierung von ![]() umkehrt“. Was mit der antipodischen Transformation von S passiert ist analog.
umkehrt“. Was mit der antipodischen Transformation von S passiert ist analog.
Die mathematischen Konzepte, die dieser heuristischen Erklärung zugrunde liegen sind Homotopie und Grad [2, 3]. Zwei Transformationen von ![]() heißen homotopisch, wenn sie stetig ineinander umgeformt werden können. Beispielsweise können zwei Drehungen von
heißen homotopisch, wenn sie stetig ineinander umgeformt werden können. Beispielsweise können zwei Drehungen von ![]() ineinander umgeformt werden, indem der Drehwinkel und die Drehachse stetig geändert werden. Andererseits kann man jeder Transformation von
ineinander umgeformt werden, indem der Drehwinkel und die Drehachse stetig geändert werden. Andererseits kann man jeder Transformation von ![]() auf sich selbst eine ganze Zahl zuweisen, den Grad. Der Grad der Identität und der Grad der antipodischen Transformation sind respektive
auf sich selbst eine ganze Zahl zuweisen, den Grad. Der Grad der Identität und der Grad der antipodischen Transformation sind respektive ![]() und
und ![]() . Der Grad einer Transformation von
. Der Grad einer Transformation von ![]() ändert sich bei einer stetigen Deformation nicht, da er in einer stetigen Deformation nicht plötzlich zu einer anderen ganzen Zahl „springen“ kann. Daher haben zwei homotopische Transformationen von
ändert sich bei einer stetigen Deformation nicht, da er in einer stetigen Deformation nicht plötzlich zu einer anderen ganzen Zahl „springen“ kann. Daher haben zwei homotopische Transformationen von ![]() den gleichen Grad und die Identitätstransformation und die antipodische Transformation sind nicht homotopisch zueinander. Wie wir gesehen haben würde ein Vektorfeld ohne Nullstellen auf einer Sphäre eine solche Homotopie liefern und damit kann dieses Vektorfeld nicht existieren. Diese Art von Argumentation, die eine diskrete Menge beinhaltet, die bei stetiger Deformation unveränderlich ist, in diesem Fall der Grad, kommt in der Topologie häufig vor.
den gleichen Grad und die Identitätstransformation und die antipodische Transformation sind nicht homotopisch zueinander. Wie wir gesehen haben würde ein Vektorfeld ohne Nullstellen auf einer Sphäre eine solche Homotopie liefern und damit kann dieses Vektorfeld nicht existieren. Diese Art von Argumentation, die eine diskrete Menge beinhaltet, die bei stetiger Deformation unveränderlich ist, in diesem Fall der Grad, kommt in der Topologie häufig vor.
Der Satz vom Igel ist auch eine Folgerung aus einem allgemeineren Satz von Poincaré über Vektorfelder auf Flächen. Sei ![]() ein stetiges Vektorfeld auf einer Fläche mit isolierter Nullstelle in
ein stetiges Vektorfeld auf einer Fläche mit isolierter Nullstelle in ![]() , das bedeutet, dass
, das bedeutet, dass ![]() der einzige Punkt in seiner Umgebung ist, wo
der einzige Punkt in seiner Umgebung ist, wo ![]() verschwindet. Es ist möglich den Index von
verschwindet. Es ist möglich den Index von ![]() in
in ![]() zu definieren, der eine ganze Zahl
zu definieren, der eine ganze Zahl ![]() ist, der die Anzahl der Drehungen von
ist, der die Anzahl der Drehungen von ![]() um
um ![]() wie folgt zählt.
wie folgt zählt.
Wir beginnen damit, einen kleinen Bereich der Fläche um p mit einem kleinen Bereich der Ebene zu bezeichnen. Dann nehmen wir einen kleinen Kreisumfang ![]() um
um ![]() , so dass
, so dass ![]() an
an ![]() entlang nie Null wird. Während man entlang
entlang nie Null wird. Während man entlang ![]() von einem beliebigen Startpunkt in irgendeine Richtung folgt, kann man der Entwicklung der Richtungen von
von einem beliebigen Startpunkt in irgendeine Richtung folgt, kann man der Entwicklung der Richtungen von ![]() folgen. Wenn man zurück zum Ausgangspunkt geht, hat
folgen. Wenn man zurück zum Ausgangspunkt geht, hat ![]() eine bestimmte Anzahl an vollen Umdrehungen ausgeführt. Jede Drehung in die gewählte Richtung zählt
eine bestimmte Anzahl an vollen Umdrehungen ausgeführt. Jede Drehung in die gewählte Richtung zählt ![]() , jede Drehung in die entgegengesetzte Richtung
, jede Drehung in die entgegengesetzte Richtung ![]() . Die Gesamtzahl der Drehungen ist der Index
. Die Gesamtzahl der Drehungen ist der Index ![]() . Der Leser kann dies für die folgenden Beispiele tun und den Wert des gegebenen Index prüfen:
. Der Leser kann dies für die folgenden Beispiele tun und den Wert des gegebenen Index prüfen:
Der Index ![]() ist auch ein topologisches Konzept, das nur vom qualitativen Verhalten von
ist auch ein topologisches Konzept, das nur vom qualitativen Verhalten von ![]() bei
bei ![]() abhängt. Tatsächlich kamen diese Ideen von Poincaré ursprünglich in einem Text vor, der den qualitativen Aspekten der Theorie der Differentialgleichungen gewidmet war.
abhängt. Tatsächlich kamen diese Ideen von Poincaré ursprünglich in einem Text vor, der den qualitativen Aspekten der Theorie der Differentialgleichungen gewidmet war.
Angenommen nun, dass ![]() ein stetiges Vektorfeld auf einer Sphäre mit isolierten Nullstellen an den Stellen
ein stetiges Vektorfeld auf einer Sphäre mit isolierten Nullstellen an den Stellen ![]() ist. Sei
ist. Sei ![]() die Summe aller Indizes von allen Nullstellen von
die Summe aller Indizes von allen Nullstellen von ![]() . Eine bemerkenswerte Tatsache, die den Leser sicher erstaunen wird, ist, dass die ganze Zahl
. Eine bemerkenswerte Tatsache, die den Leser sicher erstaunen wird, ist, dass die ganze Zahl ![]() nicht von
nicht von ![]() abhängt. Das bedeutet, wenn
abhängt. Das bedeutet, wenn ![]() ein anderes stetiges Vektorfeld auf
ein anderes stetiges Vektorfeld auf ![]() ist, mit Nullstellen in
ist, mit Nullstellen in ![]() , dann ist
, dann ist ![]() . Man nehme beispielsweise
. Man nehme beispielsweise ![]() mit einem Vektorfeld mit zwei Nullstellen vom Index
mit einem Vektorfeld mit zwei Nullstellen vom Index ![]() , wie in Abbildung 1b), von denen eine am Nordpol und eine am Südpol liegt, wobei die Summe der Indizes gleich
, wie in Abbildung 1b), von denen eine am Nordpol und eine am Südpol liegt, wobei die Summe der Indizes gleich ![]() ist. In einem anderen Beispiel kann man auch nur eine Nullstelle vom Index
ist. In einem anderen Beispiel kann man auch nur eine Nullstelle vom Index ![]() haben wie in Abbildung 3d). Der Leser kann selbst versuchen andere stetige Vektorfelder mit isolierten Nullstellen in der Sphäre zu zeichnen. Die Summe der Indizes wird immer
haben wie in Abbildung 3d). Der Leser kann selbst versuchen andere stetige Vektorfelder mit isolierten Nullstellen in der Sphäre zu zeichnen. Die Summe der Indizes wird immer ![]() sein. Dies impliziert den Satz vom Igel: wenn die Summe der Indizes der Nullstellen von
sein. Dies impliziert den Satz vom Igel: wenn die Summe der Indizes der Nullstellen von ![]()
![]() ist, das heißt nicht
ist, das heißt nicht ![]() , dann muss
, dann muss ![]() Nullstellen haben.
Nullstellen haben.
Wie lässt sich dieses Ergebnis erklären? Angenommen ![]() wird durch Dreiecke gebildet, die an den Seiten zusammengefügt sind, dann wird jede Seite von genau zwei Dreiecken geteilt. Wir nehmen an, dass die (isolierten) Nullstellen von
wird durch Dreiecke gebildet, die an den Seiten zusammengefügt sind, dann wird jede Seite von genau zwei Dreiecken geteilt. Wir nehmen an, dass die (isolierten) Nullstellen von ![]() und
und ![]() innerhalb der Dreiecke liegen, wobei jedes Dreieck höchstens eine Nullstelle von
innerhalb der Dreiecke liegen, wobei jedes Dreieck höchstens eine Nullstelle von ![]() oder
oder ![]() enthalten kann. Man richte die Seiten jedes Dreiecks so aus, dass eine kleine Ameise, die auf der Außenseite der Kugel entlang den Seiten läuft, das Innere des Dreiecks zu ihrer linken hat. Wenn eine Seite von zwei benachbarten Dreiecken
enthalten kann. Man richte die Seiten jedes Dreiecks so aus, dass eine kleine Ameise, die auf der Außenseite der Kugel entlang den Seiten läuft, das Innere des Dreiecks zu ihrer linken hat. Wenn eine Seite von zwei benachbarten Dreiecken ![]() und
und ![]() geteilt wird, dann geht die Ameise in entgegengesetzten Richtungen daran entlang, je nachdem ob sie um das Dreieck
geteilt wird, dann geht die Ameise in entgegengesetzten Richtungen daran entlang, je nachdem ob sie um das Dreieck ![]() oder
oder ![]() geht.
geht.
An jedem Punkt ![]() auf einer Seite kann man den Winkel zwischen den Vektoren
auf einer Seite kann man den Winkel zwischen den Vektoren ![]() und
und ![]() messen, der sich entlang der Kante ändert. Wenn dieser Winkel sich zwischen dem Anfang und dem Ende der Seite um ändert, wenn die Ameise in die eine Richtung läuft, dann wird er sich um
messen, der sich entlang der Kante ändert. Wenn dieser Winkel sich zwischen dem Anfang und dem Ende der Seite um ändert, wenn die Ameise in die eine Richtung läuft, dann wird er sich um ![]() ändern, wenn sie in die entgegengesetzte Richtung läuft. Wenn man also die Winkeländerung entlang aller Seiten von allen Dreiecken, die
ändern, wenn sie in die entgegengesetzte Richtung läuft. Wenn man also die Winkeländerung entlang aller Seiten von allen Dreiecken, die ![]() bilden zusammenzählt, erhält man Null, da jede Seite doppelt beiträgt, einmal für jede Richtung. Mit ein wenig Überlegung lässt sich auch feststellen, dass diese Null-Summe auch gleich
bilden zusammenzählt, erhält man Null, da jede Seite doppelt beiträgt, einmal für jede Richtung. Mit ein wenig Überlegung lässt sich auch feststellen, dass diese Null-Summe auch gleich ![]() ist. Tatsächlich ist die totale Änderung des Winkels zwischen
ist. Tatsächlich ist die totale Änderung des Winkels zwischen ![]() und
und ![]() entlang der drei Seiten des Dreiecks genau
entlang der drei Seiten des Dreiecks genau ![]() mal die Differenz der Indizes von
mal die Differenz der Indizes von ![]() und
und ![]() für die Nullstellen, wenn
für die Nullstellen, wenn ![]() und/oder
und/oder ![]() eine Nullstelle innerhalb dieses Dreiecks hat. (Da der Index die Anzahl der vollen Umdrehungen ist, die ein Vektorfeld um eine Nullstelle zurücklegt.) Wenn
eine Nullstelle innerhalb dieses Dreiecks hat. (Da der Index die Anzahl der vollen Umdrehungen ist, die ein Vektorfeld um eine Nullstelle zurücklegt.) Wenn ![]() und
und ![]() keine Nullstellen innerhalb des Dreiecks haben wird die Gesamtwinkeländerung entlang seiner drei Seiten null ergeben. Man kann im Übrigen
keine Nullstellen innerhalb des Dreiecks haben wird die Gesamtwinkeländerung entlang seiner drei Seiten null ergeben. Man kann im Übrigen ![]() definieren, wenn
definieren, wenn ![]() ist. Damit erhält man
ist. Damit erhält man ![]() , wie oben angegeben.
, wie oben angegeben.
Zusammenfassend gilt also, dass, wenn ein stetiges Vektorfeld in einer Sphäre existiert, so dass die Summe der Indizes seiner Nullstellen ![]() ist, dann gilt das für alle stetigen Vektorfelder auf seiner Fläche. Dies impliziert, wie wir gesehen haben, den Satz vom Igel.
ist, dann gilt das für alle stetigen Vektorfelder auf seiner Fläche. Dies impliziert, wie wir gesehen haben, den Satz vom Igel.
Das beschriebene Argument gilt nicht nur für Sphären, sondern für alle Flächen in Abbildung 4, die orientierbare Flächen genannt werden. Anstelle einer Sphäre kann ![]() die Fläche eines Donuts (Torus) sein oder eine andere Fläche mit
die Fläche eines Donuts (Torus) sein oder eine andere Fläche mit ![]() , wobei
, wobei ![]() die Anzahl der „Löcher“ ist.
die Anzahl der „Löcher“ ist.

Abbildung 4: Die Familie geschlossener orientierbarer Flächen:
a) die Sphäre, b) ein Torus und c) g=2, d) g>2
Es ist nicht schwierig zu zeigen, dass, wenn ![]() genau
genau ![]() Löcher hat, dann die Summe der Indizes der Nullstellen jedes stetigen Vektorfeldes auf
Löcher hat, dann die Summe der Indizes der Nullstellen jedes stetigen Vektorfeldes auf ![]() gleich der Euler-Charakteristik von
gleich der Euler-Charakteristik von ![]() , also
, also ![]() , ist [2, 6]. Anzumerken ist, dass
, ist [2, 6]. Anzumerken ist, dass ![]() nur vom lokalen Verhalten nahe bei p von X abhängt, wogegen
nur vom lokalen Verhalten nahe bei p von X abhängt, wogegen ![]() von der globalen Form der Fläche S abhängt. Im Fall der Sphäre g=0, somit ist die Summe der Indizes
von der globalen Form der Fläche S abhängt. Im Fall der Sphäre g=0, somit ist die Summe der Indizes ![]() . Im Fall des Torus
. Im Fall des Torus ![]() und man findet leicht ein stetiges Vektorfeld, das nirgends verschwindet. Dieses Argument leicht verallgemeinernd, kann man zeigen, dass dieser Satz von Poincaré auch für andere Flächen gilt, die nicht Teil dieser Familie sind, wie zum Beispiel die Projektive Ebene oder die Kleinsche Flasche [2, 5].
und man findet leicht ein stetiges Vektorfeld, das nirgends verschwindet. Dieses Argument leicht verallgemeinernd, kann man zeigen, dass dieser Satz von Poincaré auch für andere Flächen gilt, die nicht Teil dieser Familie sind, wie zum Beispiel die Projektive Ebene oder die Kleinsche Flasche [2, 5].
Später, im Jahr 1926, verallgemeinerte der deutsche Mathematiker Heinz Hopf [7] den Satz von Poincaré für Flächen geometrischer Objekte mit Dimension größer zwei. Diese Ergebnisse veranschaulichen die Vorgehensweise in der Topologie, die sich im 20. Jahrhundert stark entwickelt hat. Er findet Anwendung in vielen Gebieten der Mathematik, wie Geometrie, Analysis, dynamischen Systemen und Differentialgleichungen, und charakterisiert die qualitativen und globalen Aspekte fraglichen Probleme.
Man kann die horizontale Komponente der Geschwindigkeit von Luft in der Atmosphäre bei einer bestimmten Höhenlage durch ein stetiges Vektorfeld auf der Oberfläche einer Sphäre modellieren. Der Satz vom Igel sagt dann die Existenz von Nullstellen voraus, sowie die entstehenden Wirbel, wie beispielsweise Zyklonen, in der Bewegung der Atmosphäre. Genauso gilt er für die Bewegung von ultraheißen Gasen in der Atmosphäre der Sonne, die ständig imposante Wirbel bilden. Ein Teil der Schönheit der mathematischen Sprache rührt von der Beschreibung her, die Phänomene so unterschiedlich wie unsere morgendliche Frisur und die Atmosphäre der Sonne durch dasselbe Begriffssystem vereint, das mit großer Wirksamkeit sowohl auf die physikalische Welt als auch die abstraktesten Probleme angewandt werden kann.
Quellen:
[1] http://pt.wikipedia.org/wiki/Henri_Poincaré, http://www.poincare.fr
[2] W. Fulton, Algebraic Topology – a first course, Springer-Verlag 1995.
[3] E.L. Lima, Curso de Analise, Vol.2, Chapter VII, Projecto Euclides, IMPA, 1981.
[4] http://en.wikipedia.org/wiki/Hairy_ball_theorem
[5] http://en.wikipedia.org/wiki/Real_projective_plane, http://en.wikipedia.org/wiki/Klein_bottle
[6] http://en.wikipedia.org/wiki/Euler_characteristic
[7] http://en.wikipedia.org/wiki/Heinz_Hopf
Andere Sprachen: Englisch, Arabisch, Portugiesisch, Brasilien

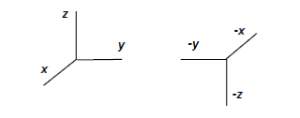
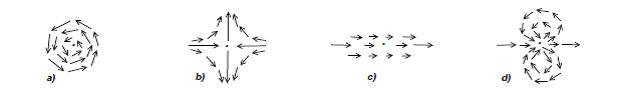
 Deutsch
Deutsch 简体中文
简体中文  English
English  Français
Français  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português