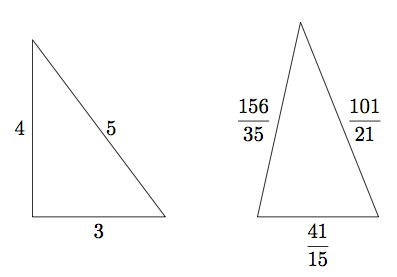 Autor: William McCallum (University of Arizona)
Autor: William McCallum (University of Arizona)
Übersetzt von Anna Muff und Hans-Georg Weigand (Universität Würzburg)
Wenn zwei Dreiecke denselben Flächeninhalt und denselben Umfang haben, sind sie dann notwendigerweise kongruent? Wie sich herausstellt ist die Antwort nein. Ein Dreieck mit den Seitenlängen ![]() ,
, ![]() und
und ![]() hat beispielsweise denselben Flächeninhalt und Umfang wie ein Dreieck mit den Seitenlängen
hat beispielsweise denselben Flächeninhalt und Umfang wie ein Dreieck mit den Seitenlängen ![]() ,
, ![]() und
und ![]() .
.
Der Umfang beider Dreiecke ist ![]() :
:
![]()
Erstaunlicherweise haben diese beiden Dreiecke auch denselben Flächeninhalt. Das rechtwinklige Dreieck hat den Flächeninhalt ![]() .
.
Um den Flächeninhalt des anderen Dreiecks zu berechnen benutzen wir den Satz des Heron, der aussagt, dass der Flächeninhalt ![]() eines Dreiecks mit den Seiten
eines Dreiecks mit den Seiten ![]() ,
, ![]() und
und ![]() gegeben ist durch
gegeben ist durch
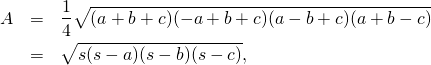
wobei ![]() den halben Umfang des Dreiecks angibt. Durch eine kurze Rechnung, die diese Formel benutzt, zeigt sich, dass der Flächeninhalt des zweiten Dreiecks auch
den halben Umfang des Dreiecks angibt. Durch eine kurze Rechnung, die diese Formel benutzt, zeigt sich, dass der Flächeninhalt des zweiten Dreiecks auch ![]() ist.
ist.
Der Raum der Dreiecke
Wie kann man solche Beispiele finden? Das Geheimnis liegt darin, den richtigen Weg zu finden, alle Dreiecke darzustellen. Dafür gibt es viele Möglichkeiten. Eine davon ist es, ein Dreieck durch das Tripel ![]() anzugeben, das aus einer Anordnung der Seitenlängen besteht. Auf diese Weise stellt man ein Dreieck als einen Punkt im
anzugeben, das aus einer Anordnung der Seitenlängen besteht. Auf diese Weise stellt man ein Dreieck als einen Punkt im ![]() dar. Nicht jeder Punkt entspricht einem Dreieck; es müssen zum Beispiel alle Koordinaten positiv sein. Gibt es noch andere Einschränkungen?
dar. Nicht jeder Punkt entspricht einem Dreieck; es müssen zum Beispiel alle Koordinaten positiv sein. Gibt es noch andere Einschränkungen?
Koordinaten können auch auf andere Weise im Raum der Dreiecke dargestellt werden, nämlich indem man anstelle von Längen Winkel benutzt. Jedes Dreieck hat einen Inkreis und der Radius dieses Kreises steht in einfacher Relation zum Flächeninhalt ![]() und zum halbem Umfang
und zum halbem Umfang ![]() , nämlich
, nämlich
![]()
Um zu sehen, warum das gilt, fällt man Lote vom Kreismittelpunkt auf die Seiten des Dreiecks, wie in der linken Figur in Abbildung 2. Diese Lote bilden die Höhen von drei kleineren Dreiecken mit dem Lotfußpunkt auf den jeweiligen Seiten des großen Dreiecks und einer Ecke am Mittelpunkt des Inkreises. Durch Addition der Flächeninhalte dieser Dreiecke erhält man ![]() .
.
-

- Abbildung 2: Parametrisierung des Raums der Dreiecke
Diese Gleichung gibt an, dass auch die Radien der Inkreise gleich sind, wenn zwei Dreiecke denselben Flächeninhalt und Umfang haben. Wenn man also nach zwei solchen Dreiecken sucht, wird man sie unter allen Dreiecken finden, die um einen festen Inkreis liegen. Anstatt für die Beschreibung dieser Dreiecke Längenangaben zu benutzen, wählt man die Winkel, die, wie im rechten Dreieck in Abbildung 2, am Inkreismittelpunkt liegen.
Parametrisierung von Dreiecken mit konstantem Flächeninhalt und Umfang
Im Raum der Dreiecke finden sich Kurven, die einer ganzen Familie von Dreiecken mit denselben Werten ![]() und
und ![]() entsprechen.
entsprechen.
Zunächst wird ![]() durch die Winkel
durch die Winkel ![]() ,
, ![]() und
und ![]() und durch
und durch ![]() , den Radius des Inkreises, folgendermaßen ausgedrückt: Die Radien und die Strecken von den Eckpunkten zum Inkreismittelpunkt teilen das Dreieck in sechs rechtwinklige Dreiecke. Da die Strecken von den Ecken zum Mittelpunkt die Winkel des großen Dreiecks halbieren, treten die rechtwinkligen Dreiecke in kongruenten Paaren auf. Durch die Grundseitenlänge je eines Paares und Addition dieser erhält man
, den Radius des Inkreises, folgendermaßen ausgedrückt: Die Radien und die Strecken von den Eckpunkten zum Inkreismittelpunkt teilen das Dreieck in sechs rechtwinklige Dreiecke. Da die Strecken von den Ecken zum Mittelpunkt die Winkel des großen Dreiecks halbieren, treten die rechtwinkligen Dreiecke in kongruenten Paaren auf. Durch die Grundseitenlänge je eines Paares und Addition dieser erhält man
![]()
Diese Gleichung gibt zusammen mit ![]() an, wenn der Flächeninhalt
an, wenn der Flächeninhalt ![]() und der halbe Umfang
und der halbe Umfang ![]() konstant sind, dass für die Summe der Tangenten gilt:
konstant sind, dass für die Summe der Tangenten gilt:
(1) ![]()
Als nächstes wird dies in eine Gleichung übersetzt, die eine Kurve in der Ebene beschreibt. Es werden ![]() ,
, ![]() und
und ![]() gesetzt. Da
gesetzt. Da ![]() ergibt, ist
ergibt, ist
![]()
, also
![]()
Gleichung (1) wird für ein festes ![]() , wenn
, wenn ![]() die Konstante
die Konstante ![]() ist, zur Gleichung
ist, zur Gleichung
(2) ![]()
(3) ![]()
Jedes Dreieck mit Flächeninhalt ![]() und halbem Umfang
und halbem Umfang ![]() gibt einen Punkt auf dieser Kurve an, und jeder Punkt auf der Kurve in einem bestimmten Bereich der Ebene entspricht einem Dreieck. Der Bereich entspricht den Winkeln, wie Abbildung 2 zeigt, die
gibt einen Punkt auf dieser Kurve an, und jeder Punkt auf der Kurve in einem bestimmten Bereich der Ebene entspricht einem Dreieck. Der Bereich entspricht den Winkeln, wie Abbildung 2 zeigt, die ![]() und
und ![]() erfüllen, was dem Bereich
erfüllen, was dem Bereich ![]() ,
, ![]() und
und ![]() (da
(da ![]() ) entspricht.
) entspricht.
Die folgende Abbildung zeigt diese Kurve für ![]() , den Wert, der dem Dreieck mit den Seitenlängen
, den Wert, der dem Dreieck mit den Seitenlängen ![]() ,
, ![]() und
und ![]() entspricht. Jeder Punkt auf dem Graphen im positiven Quadranten entspricht einem Dreieck; die Seitenlängen des Dreiecks sind
entspricht. Jeder Punkt auf dem Graphen im positiven Quadranten entspricht einem Dreieck; die Seitenlängen des Dreiecks sind ![]() ,
, ![]() und
und ![]() . Im Speziellen entsprechen die Punkte
. Im Speziellen entsprechen die Punkte ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() und
und ![]() alle dem Dreieck mit den Seitenlängen
alle dem Dreieck mit den Seitenlängen ![]() ,
, ![]() und
und ![]() , jeweils mit den Seitenlängen in verschiedener Reihenfolge.
, jeweils mit den Seitenlängen in verschiedener Reihenfolge.
Diese Abbildung ist interaktiv: Probieren Sie aus, was für andere Punkte auf der Kurve oder andere Werte für Flächeninhalt und Umfang passiert!
Punkte auf der Kurve finden
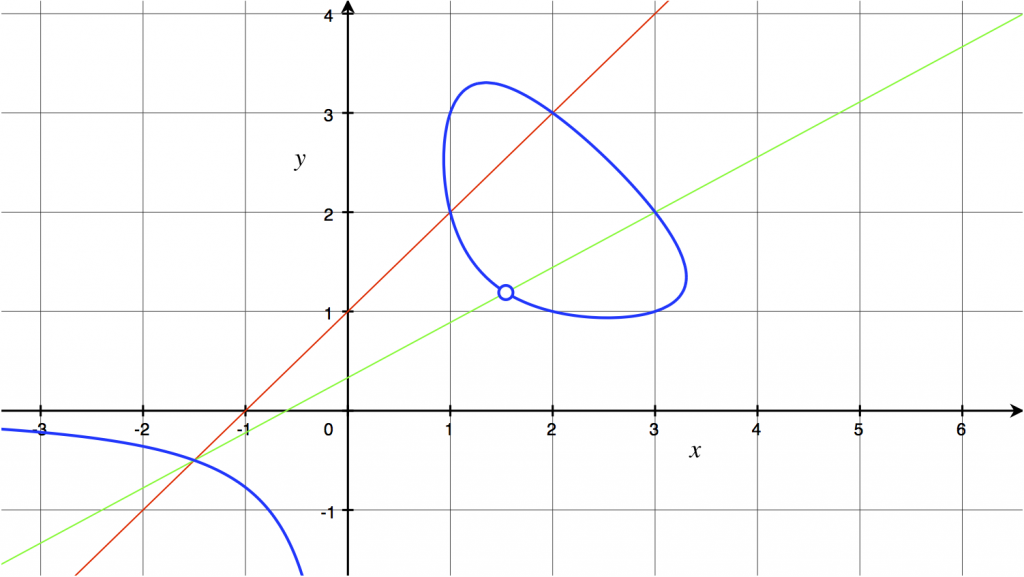
Abbildung 3: Kurve, die Dreiecke mit Umfang 12 und Flächeninhalt 6 parametrisiert.
Da die Kurve in Abbildung 3 durch eine Gleichung dritten Grades definiert ist, kann man durch das Tangenten- und Sekantenverfahren Punkte finden. Zwei Punkte auf der Kurve geben eine Sekante an, die die Kurve in einem weiteren Punkt schneidet; diesen Punkt zu finden führt zur Lösung einer kubischen Gleichung in ![]() , von der bereits zwei Nullstellen bekannt sind. Da man schon sechs Punkte auf der Kurve hat, gibt es viele Möglichkeiten für Sekanten. Das Errechnen von mehr Punkten schafft noch mehr Möglichkeiten. Tatsächlich hat die Kurve unendlich viele Punkte mit rationalen Koordinaten. Die Vorgehensweise mit zwei Sekanten, wie in Abbildung 3, führt zum Punkt
, von der bereits zwei Nullstellen bekannt sind. Da man schon sechs Punkte auf der Kurve hat, gibt es viele Möglichkeiten für Sekanten. Das Errechnen von mehr Punkten schafft noch mehr Möglichkeiten. Tatsächlich hat die Kurve unendlich viele Punkte mit rationalen Koordinaten. Die Vorgehensweise mit zwei Sekanten, wie in Abbildung 3, führt zum Punkt ![]() (durch einen Kreis gekennzeichnet), der dem Dreieck mit den Seiten
(durch einen Kreis gekennzeichnet), der dem Dreieck mit den Seiten ![]() ,
, ![]() und
und ![]() entspricht.
entspricht.
Das Sekantenverfahren gelingt für jede kubische Kurve in der Ebene; solche Kurven nennt man elliptische Kurven (nicht weil sie selbst Ellipsen sind, sondern weil sie im Forschungsgebiet gewisser komplexer Funktionsklassen, die elliptische Funktionen genannt werden, auftreten). Das Sekantenverfahren erlaubt die Definition einer Gruppenstruktur auf rationalen Punkten auf einer elliptischen Kurve (das bedeutet Punkte, deren Koordinaten rationale Zahlen sind). Das Studium elliptischer Kurven ist ein zentrales Gebiet in der Zahlentheorie mit Anwendung in Verschlüsselungsprogrammen für sichere Finanztransaktionen im Internet. Elliptische Kurven spielten im Beweis des Großen Fermatschen Satzes eine zentrale Rolle.
Die Geschichte, die in diesem Artikel beschrieben ist, zeigt die bemerkenswerte Geschlossenheit der Mathematik, wie sie am Gymnasium beginnt, bis hin zur Forschung. Auf dem Weg sind wir auf eine fundamentale Idee der modernen Mathematik gestoßen: die Idee, ein Problem mithilfe einer bestimmten Art von Objekt (beispielsweise Dreiecke mit Flächeninhalt 6 und Umfang 12) zu lösen, indem man das Objekt in einen allgemeineren Raum überträgt (den Raum aller Dreiecke) und den richtigen Weg findet, diesen Raum zu parametrisieren.
Andere Sprachen: Vereinfachtes Chinesisch, Englisch, Französisch, Italienisch, Spanisch, Arabisch, Khmer, Portugiesisch, Brasilien

 Deutsch
Deutsch 简体中文
简体中文  English
English  Français
Français  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português