 A autora original é Michèle Artigue. Traduzido por Pedro Malagutti (UFSCar, Brasil) e Cydara Cavedon Ripoll (UFRGS, Brasil).
A autora original é Michèle Artigue. Traduzido por Pedro Malagutti (UFSCar, Brasil) e Cydara Cavedon Ripoll (UFRGS, Brasil).
Os infinitesimais desempenharam um papel essencial no surgimento e desenvolvimento do cálculo diferencial e integral. O ganho evidente com esse cálculo não impediu, contudo, recorrentes debates sobre a natureza de tais objetos e a legitimidade de seu uso. Ao final do século XIX, quando a construção dos números reais a partir dos inteiros e a definição moderna da noção de limite forneceram as fundações sólidas ao cálculo diferencial e integral, os infinitesimais e a metafísica que os cerca foram rechaçados, e o seu uso passou a ser percebido como sinônimo de práticas pouco rigorosas e doravante então encerradas. No entanto, a linguagem dos infinitesimais continuou sendo utilizada, por exemplo, na física e, mesmo na matemática, ela nunca desapareceu completamente do discurso informal e do pensamento heurístico de muitos pesquisadores.
Afinal, é esta linguagem realmente incompatível com o rigor matemático? E o que ela oferece de interessante, de específico que explica sua permanência?
A análise não standard desenvolvida no século XX permitiu responder estas questões, e, aos infinitesimais, permitiu terem a sua revanche.
Do cálculo infinitesimal à análise não standard
No prefácio do primeiro tratado de análise infinitesimal publicado em 1696, seu autor, o Marquês de l´Hôpital, evidencia a potência e a facilidade do novo cálculo que os infinitesimais permitem![]() :
:

Figura 1 : Capa e recorte do prefácio do tratado do Marquês de l´Hôpital
Mas logo os debates se desenvolveram em torno de tais objetos e de seu uso. Em um célebre texto publicado em 1734, The Analyst, George Berkeley fez uma crítica feroz ao uso dos infinitesimais ou incrementos evanescentes no cálculo diferencial, e Jean Le Rond d’Alembert, em l’Encyclopédie Méthodique de 1751, quer já deles se liberar, amparando-se na ideia de limite. Na virada do século XX, com o desenvolvimento da análise moderna, isto passa a parecer estabelecido. No entanto, meio século mais tarde, os trabalhos de Abraham Robinson vão reabilitar os infinitesimais e as práticas a eles associadas.
Abraham Robinson mostra que, de fato, a linguagem dos infinitesimais é totalmente compatível com o rigor matemático. O lógico Thoralf Skolem já havia mostrado, em 1934, que o conjunto obtido pela adição sucessiva de unidades a partir do 0 não poderia ser o único modelo para a axiomática de Peano, e que existem, portanto, modelos diferentes, ditos não standard, desta aritmética. Em 1961, Abraham Robinson mostra, ele mesmo, por uma construção baseada em ultraprodutos, a existência de um modelo não standard de números reais contendo os números « infinitamente grandes » e « infinitamente pequenos ». Nasce assim a Análise não Standard (ANS). Depois, Edward Nelson, em 1977, acha um modo de axiomatizar a ANS. Para isso, ele junta à linguagem da teoria dos conjuntos um símbolo para um predicado unário, ![]() , para expressar que um objeto
, para expressar que um objeto ![]() é standard, e, à axiomática ZFC
é standard, e, à axiomática ZFC![]() para essa teoria, junta três axiomas: os axiomas de idealização, de standardização e de transferência
para essa teoria, junta três axiomas: os axiomas de idealização, de standardização e de transferência![]() , o que torna a ANS mais confortavelmente manipulável. É sobre esta axiomatização denominada IST (Teoria de Conjuntos Interna) que nos apoiamos nesta vinheta.
, o que torna a ANS mais confortavelmente manipulável. É sobre esta axiomatização denominada IST (Teoria de Conjuntos Interna) que nos apoiamos nesta vinheta.
Estes três axiomas têm consequências importantes. Decorre, por exemplo, do axioma de transferência que dois conjuntos standard E1 e E2 são iguais se e somente se eles possuem os mesmos elementos standard![]() . Decorre deste mesmo axioma que se existe um
. Decorre deste mesmo axioma que se existe um ![]() que verifica uma propriedade clássica
que verifica uma propriedade clássica ![]() , isto é, uma propriedade que pode ser expressa sem se fazer uso do predicado st, então existe necessariamente um
, isto é, uma propriedade que pode ser expressa sem se fazer uso do predicado st, então existe necessariamente um ![]() standard que a verifica. Os objetos que se pode definir de maneira única por uma fórmula clássica são, portanto, necessariamente objetos standard. Os números e os objetos usuais com os quais nos defrontamos em matemática (os números
standard que a verifica. Os objetos que se pode definir de maneira única por uma fórmula clássica são, portanto, necessariamente objetos standard. Os números e os objetos usuais com os quais nos defrontamos em matemática (os números ![]() ,
, ![]() , as funções trigonométricas e exponenciais) são, assim, objetos standard, bem como o conjunto vazio, o conjunto
, as funções trigonométricas e exponenciais) são, assim, objetos standard, bem como o conjunto vazio, o conjunto ![]() dos inteiros e o conjunto
dos inteiros e o conjunto ![]() dos números reais.
dos números reais.
Mas ser um conjunto standard não implica conter exclusivamente elementos standard. De fato, decorre do axioma da idealização que existe um inteiro superior a todos os inteiros standard e que, mais geralmente, todo conjunto infinito contém, necessariamente, ao menos um elemento não standard![]() .
. ![]() e
e ![]() são, assim, conjuntos standard que contêm elementos não standard. Como representá-los?
são, assim, conjuntos standard que contêm elementos não standard. Como representá-los?
Em ![]() , todos os inteiros standard precedem os inteiros não standard. Em
, todos os inteiros standard precedem os inteiros não standard. Em ![]() , a situação é um pouco mais complicada. Distinguimos, de fato, de acordo com seu tamanho, três tipos de reais:
, a situação é um pouco mais complicada. Distinguimos, de fato, de acordo com seu tamanho, três tipos de reais:
- os reais muito pequenos ou infinitesimais (positivos e negativos), aqueles cujo valor absoluto é menor do que qualquer real standard positivo,
- os reais muito grandes ou infinitamente grandes (positivos e negativos), aqueles cujo valor absoluto é maior do que qualquer real standard positivo,
- entre os dois, os reais na escala humana, por assim dizer, frequentemente denominados apreciáveis.
Se um real é infinitesimal ou apreciável, dizemos que é limitado. Se um real é infinitamente grande, seu inverso é um infinitesimal e são ambos necessariamente não standard. No entanto, os reais apreciáveis podem ser standard ou não. Consideremos, por exemplo, o real ![]() ; acrescentando-lhe um real
; acrescentando-lhe um real ![]() infinitesimal não nulo, obtemos o real
infinitesimal não nulo, obtemos o real ![]() , também apreciável, mas não standard e infinitamente próximo de
, também apreciável, mas não standard e infinitamente próximo de ![]() . Ao redor de cada real standard existe, assim, uma nuvem de reais não standard que lhe são infinitamente próximos. Para dar conta disto, introduzimos uma nova relação. Dizemos que
. Ao redor de cada real standard existe, assim, uma nuvem de reais não standard que lhe são infinitamente próximos. Para dar conta disto, introduzimos uma nova relação. Dizemos que ![]() está infinitamente próximo de
está infinitamente próximo de ![]() si
si ![]() é um infinitesimal, o que se denota por
é um infinitesimal, o que se denota por ![]() , e chamamos de halo de um real a coleção dos reais que lhe são infinitamente próximos. Os infinitesimais de fato são o halo de
, e chamamos de halo de um real a coleção dos reais que lhe são infinitamente próximos. Os infinitesimais de fato são o halo de ![]() e qualquer real apreciável
e qualquer real apreciável ![]() pertence ao halo de um único real standard que se chama sua parte standard. Podemos imaginar a reta real, como mostrado na figura 2, com uma fronteira não claramente marcada entre reais apreciáveis e reais infinitamente grandes, porque a coleção dos apreciáveis não tem um maior elemento, tampouco a coleção dos infinitamente grandes positivos tem um menor elemento.
pertence ao halo de um único real standard que se chama sua parte standard. Podemos imaginar a reta real, como mostrado na figura 2, com uma fronteira não claramente marcada entre reais apreciáveis e reais infinitamente grandes, porque a coleção dos apreciáveis não tem um maior elemento, tampouco a coleção dos infinitamente grandes positivos tem um menor elemento.

Figura 2: Representação da reta real não standard
As regras de cálculo, levando em conta as diferenças de ordem de grandeza dos números reais, estendem as da aritmética. Assim, denotando por ![]() os infinitesimais, por
os infinitesimais, por ![]() os apreciáveis e por
os apreciáveis e por ![]() os infinitamente grandes, temos por exemplo:
os infinitamente grandes, temos por exemplo:
![]() ,
, ![]() ,
, ![]() e
e ![]() .
.
Convidamos o leitor a completar, quando possível, os casos nas duas tabelas seguintes.
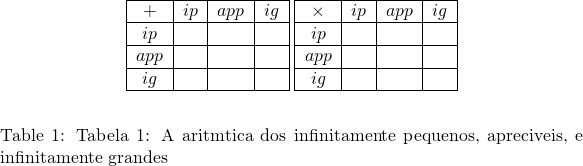
Assim, o conjunto dos números reais sempre satisfaz o princípio de Arquimedes: se ![]() e
e ![]() são reais positivos e
são reais positivos e ![]() , existe um inteiro
, existe um inteiro ![]() tal que
tal que ![]() , mas é claro que se
, mas é claro que se ![]() é infinitamente pequeno, e se
é infinitamente pequeno, e se ![]() não o é,
não o é, ![]() é necessariamente infinitamente grande.
é necessariamente infinitamente grande.
A ANS e as noções básicas da análise
No escopo da ANS, os conceitos básicos da análise matemática (limites, continuidade, derivabilidade, integrabilidade) são formalizados de maneira muito simples para os objetos standard, como se vê na seguinte tabelai![]() :
:

Estas formalizações simples sem alternâncias de quantificadores, e as ideias subjacentes permitem demonstrações simplificadas de muitos teoremas clássicos.
No quadro abaixo está proposta uma demonstração do teorema do valor intermediário.
|
Teorema do valor intermediário
Seja |
A ANS também permite justificar as técnicas de particionar em fatias infinitesimais há muito utilizadas fora da comunidade matemática para calcular áreas, volumes, momentos de inércia, centros de gravidade… ou para modelizar situações utilizando equações diferenciais. O exemplo a seguir é uma ilustração particularmente simples deste fato.
Cálculo do volume da esfera:
Seja ![]() uma esfera de raio
uma esfera de raio ![]() . A esfera pode ser particionada em fatias de espessura infinitesimal
. A esfera pode ser particionada em fatias de espessura infinitesimal ![]() .
.
O volume ![]() da fatia situada na altura
da fatia situada na altura ![]() é aproximadamente igual ao do cilindro de raio
é aproximadamente igual ao do cilindro de raio ![]() e altura
e altura ![]() :
:
![]() .
.
Daí, somando-se, obtemos:
![]()
![]()
e, finalmente, ![]() .
.
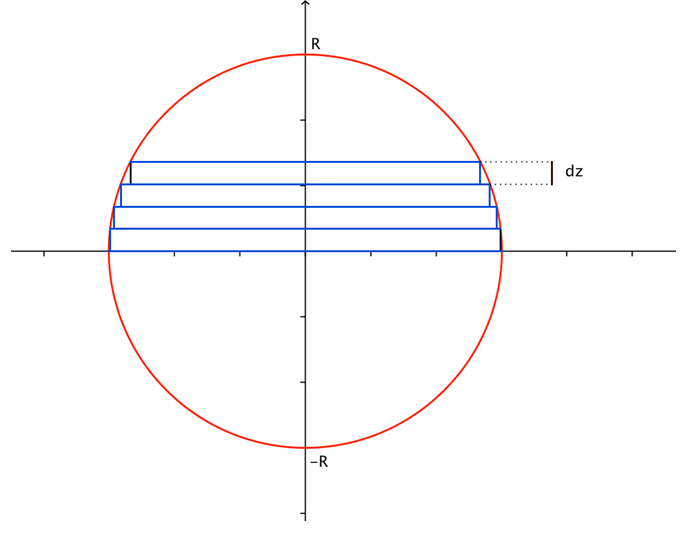
Figura 3: O volume da esfera
A soma dos volumes dos cilindros infinitesimais é precisamente a soma de Cauchy associada à subdivisão de passo infinitesimal ![]() do intervalo
do intervalo ![]() para a função área
para a função área ![]() .
.
A parte standard desta soma é pois igual, pela definição não standard da integral de uma função contínua, à integral ![]() . Contudo, o fato de esta integral dar precisamente o volume da esfera repousa no fato de que a aproximação proposta fornece um volume equivalente ao volume da fatia, e não só um volume infinitamente próximo. Este não seria o caso se se utilizasse a mesma aproximação por cilindros para calcular a área da esfera, por exemplo.
. Contudo, o fato de esta integral dar precisamente o volume da esfera repousa no fato de que a aproximação proposta fornece um volume equivalente ao volume da fatia, e não só um volume infinitamente próximo. Este não seria o caso se se utilizasse a mesma aproximação por cilindros para calcular a área da esfera, por exemplo.
A necessidade de certa vigilância
Manipular objetos não standard, requer, contudo, um pouco de vigilância. Por exemplo, ampliando a definição anterior de continuidade a uma função e número real quaisquer, standard ou não, obtém-se uma noção: a ![]() -continuidade em um ponto, que não necessariamente corresponde a nossa visão de funções contínuas. Por exemplo, a função degrau que vale
-continuidade em um ponto, que não necessariamente corresponde a nossa visão de funções contínuas. Por exemplo, a função degrau que vale ![]() para reais estritamente negativos e
para reais estritamente negativos e ![]() para reais positivos, com
para reais positivos, com ![]() infinitamente pequeno é
infinitamente pequeno é ![]() -contínua em
-contínua em ![]() , já que a imagem de qualquer infinitesimal positivo é o infinitesimal
, já que a imagem de qualquer infinitesimal positivo é o infinitesimal ![]() . Por outro lado, a função elevar ao quadrado não é
. Por outro lado, a função elevar ao quadrado não é ![]() -contínua em
-contínua em ![]() , se
, se ![]() for infinitamente grande, já que
for infinitamente grande, já que ![]() não está infinitamente próximo de
não está infinitamente próximo de ![]() . De fato, para funções standard, a
. De fato, para funções standard, a ![]() -continuidade em qualquer ponto de
-continuidade em qualquer ponto de ![]() equivale à continuidade uniforme sobre
equivale à continuidade uniforme sobre ![]() , e o cálculo que acabamos de fazer para a função elevar ao quadrado mostra, muito simplesmente, que esta função não é uniformemente contínua sobre
, e o cálculo que acabamos de fazer para a função elevar ao quadrado mostra, muito simplesmente, que esta função não é uniformemente contínua sobre ![]() .
.
O uso da ANS também requer cuidado com o uso do princípio de indução. Na sua forma usual, ele se aplica a propriedades clássicas, isto é, ele é uma consequência do axioma de transferência, mas não mais além.
|
Seja
|
O princípio de indução é aplicado aqui a um enunciado não clássico, porque está escrito com o predicado ![]() . O raciocínio não é nada paradoxal. Ele simplesmente não é válido. De fato, se mostra que para uma propriedade
. O raciocínio não é nada paradoxal. Ele simplesmente não é válido. De fato, se mostra que para uma propriedade ![]() qualquer, somente é válido o princípio de recorrência restrito seguinte: Se
qualquer, somente é válido o princípio de recorrência restrito seguinte: Se ![]() é verdadeira e se, para qualquer inteiro
é verdadeira e se, para qualquer inteiro ![]() ,
, ![]() implica
implica ![]() , então
, então ![]() é certa para todo inteiro standard.
é certa para todo inteiro standard.
As potencialidades da ANS: uma questão ainda debatida
Como vemos, a ANS reabilita os infinitesimais, os métodos de cálculo e as intuições que os acompanham, mas isto a custa de certo trabalho e certa vigilância. Então, o que se ganha realmente com a ANS? A questão segue sendo objeto de debate, como mostra, por exemplo, o blog do matemático Terence Tao, o qual acessamos ao preparar esta vinheta. A ANS é utilizada em diversas áreas da matemática, em particular topologia, probabilidade, sistemas dinâmicos. Também tem alimentado modelizações interessantes, por exemplo, em automação, ecologia, economia. Na França, por exemplo, por iniciativa de Georges Reeb, uma comunidade se desenvolveu desde o final dos anos 70 sendo a ela creditados resultados originais em muitas áreas (ver (Lutz y Goze , 1982 ), ( Diener y Diener, 1995 )). Um dos mais conhecidos é o descobrimento de trajetórias chamadas “patos” em campos de vetores lentos-rápidos em duas e, posteriormente, três dimensões. Nós o apresentamos a seguir, a título de exemplo, sem entrar contudo nos detalhes técnicos de seu tratamento não standard. O leitor pouco familiarizado com as equações diferenciais, pode pular esta parte.
As trajetórias « pato »
Consideremos a equação diferencial ![]() com
com ![]() e
e ![]() . Um estudo clássico desta equação mostra que se
. Um estudo clássico desta equação mostra que se ![]() , a equação admite uma única solução periódica que é um ciclo limite atrator. Esta solução periódica desaparece para
, a equação admite uma única solução periódica que é um ciclo limite atrator. Esta solução periódica desaparece para ![]() quando existe então um estado atrator estacionário
quando existe então um estado atrator estacionário ![]() . O fenômeno das trajetórias pato que precede esta bifurcação da dinâmica, conhecida como bifurcação de Hopf, é evidenciada para valores de
. O fenômeno das trajetórias pato que precede esta bifurcação da dinâmica, conhecida como bifurcação de Hopf, é evidenciada para valores de ![]() muito pequenos e valores de a muito próximos de
muito pequenos e valores de a muito próximos de ![]() . Uma modelização não standard, supondo
. Uma modelização não standard, supondo ![]() infinitamente pequeno, permitiu identificar o fenômeno e caracterizar as condições de sua aparição.
infinitamente pequeno, permitiu identificar o fenômeno e caracterizar as condições de sua aparição.
Inicialmente transformamos a equação em um sistema, e o fazemos de duas maneiras diferentes: seja pondo ![]() with
with ![]() , uma transformação clássica para estudar este tipo de equação, dita de Lienard, seja de forma clássica, pondo
, uma transformação clássica para estudar este tipo de equação, dita de Lienard, seja de forma clássica, pondo ![]() . Daí os dois sistemas, sendo
. Daí os dois sistemas, sendo ![]() um real infinitamente grande:
um real infinitamente grande:
![]()
![]()
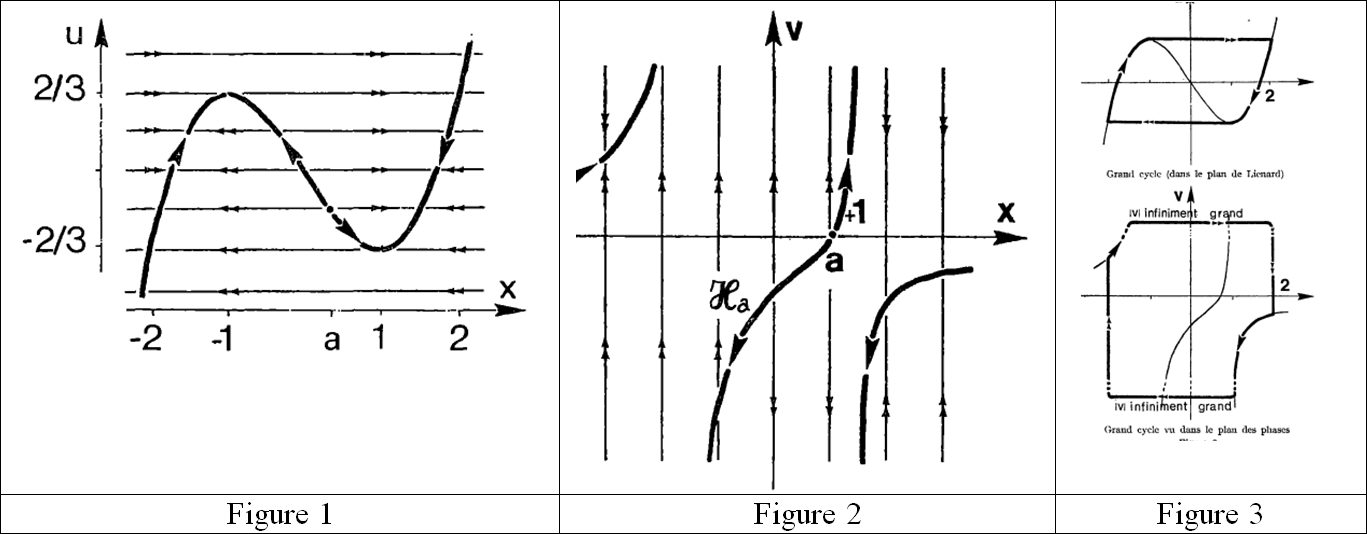
Os campos associados nos planos ![]() e
e ![]() são reproduzidos nas figuras 1 e 2, extraídas de (Benoît et al., 1981). São campos lentos-rápidos. Por exemplo, o campo do plano
são reproduzidos nas figuras 1 e 2, extraídas de (Benoît et al., 1981). São campos lentos-rápidos. Por exemplo, o campo do plano ![]() ou plano de Lienard, é quase horizontal fora do halo da cúbica
ou plano de Lienard, é quase horizontal fora do halo da cúbica ![]() de equação
de equação ![]() cujas partes crescentes são atratoras, dada a direção das flechas horizontais, enquanto que a parte decrescente é repulsora. As flechas duplas indicam que estas partes quase-horizontais são percorridas com uma velocidade infinitamente alta. Mostra-se, por meio da combinação de técnicas de análise clássica e de análise não standard, especialmente com o uso de mudanças de escala, ampliações infinitamente grandes em uma direção nos planos
cujas partes crescentes são atratoras, dada a direção das flechas horizontais, enquanto que a parte decrescente é repulsora. As flechas duplas indicam que estas partes quase-horizontais são percorridas com uma velocidade infinitamente alta. Mostra-se, por meio da combinação de técnicas de análise clássica e de análise não standard, especialmente com o uso de mudanças de escala, ampliações infinitamente grandes em uma direção nos planos ![]() e
e ![]() que, quando
que, quando ![]() e fora do halo de
e fora do halo de ![]() , há um único grande ciclo atrator (figura 3). No plano
, há um único grande ciclo atrator (figura 3). No plano ![]() , uma partícula seguindo neste ciclo, a partir, por exemplo, de um ponto
, uma partícula seguindo neste ciclo, a partir, por exemplo, de um ponto ![]() não situado no halo de
não situado no halo de ![]() , se move quase horizontalmente a uma velocidade infinitamente alta até chegar no halo de
, se move quase horizontalmente a uma velocidade infinitamente alta até chegar no halo de ![]() , nele permanecendo com uma velocidade apreciável
, nele permanecendo com uma velocidade apreciável ![]() até chegar ao halo de seu mínimo local
até chegar ao halo de seu mínimo local ![]() . Em seguida ela retoma sua trajetória quase horizontal até chegar de novo no halo de
. Em seguida ela retoma sua trajetória quase horizontal até chegar de novo no halo de ![]() e segui-lo até o halo do máximo local
e segui-lo até o halo do máximo local ![]() , antes de retomar o movimento horizontal.
, antes de retomar o movimento horizontal.
Quando ![]() , a situação se complica, pois ramos separados da curva
, a situação se complica, pois ramos separados da curva ![]() associada a
associada a ![]() no plano de fase da equação se tornam infinitamente próximos. Resulta que, no plano
no plano de fase da equação se tornam infinitamente próximos. Resulta que, no plano ![]() , uma solução que seguiu ao longo de
, uma solução que seguiu ao longo de ![]() até chegar no halo de
até chegar no halo de ![]() , pode, para certos valores de a, seguir ao longo de uma porção da parte repulsora de
, pode, para certos valores de a, seguir ao longo de uma porção da parte repulsora de ![]() antes de se tornar quase horizontal e alcançar o halo da parte atratora de
antes de se tornar quase horizontal e alcançar o halo da parte atratora de ![]() (figura 4).
(figura 4).
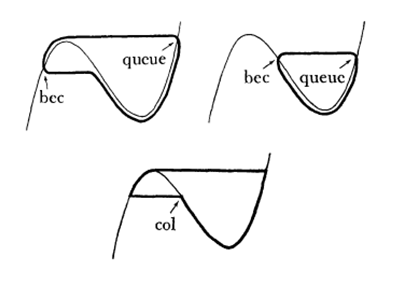
Figura 4 : Morfologia dos patos
É devido a estes ciclos que, por sua forma, os pesquisadores deram o nome de pato, mostrando, por exemplo, que para todo ![]() entre
entre ![]() y
y ![]() , existe um valor de a para o qual existe um ciclo pato cujo pico tem
, existe um valor de a para o qual existe um ciclo pato cujo pico tem ![]() por abscissa. Sem o apoio da modelização ANS, a existência de tais trajetórias poderia ter permanecido ignorada. De fato, para observá-las, não é suficiente que c seja pequeno e a próximo a
por abscissa. Sem o apoio da modelização ANS, a existência de tais trajetórias poderia ter permanecido ignorada. De fato, para observá-las, não é suficiente que c seja pequeno e a próximo a ![]() ; mostra-se que é necessário que
; mostra-se que é necessário que ![]() esteja muito perto de
esteja muito perto de ![]() , mais precisamente, que o quociente
, mais precisamente, que o quociente ![]() seja infinitamente pequeno. A existência destas trajetórias patos, evidenciada em sistemas em duas e três dimensões, além de seu interesse puramente matemático, possui diversas aplicações.
seja infinitamente pequeno. A existência destas trajetórias patos, evidenciada em sistemas em duas e três dimensões, além de seu interesse puramente matemático, possui diversas aplicações.
Contudo deve-se ressaltar que os novos resultados que a ANS permitiu obter foram muitas vezes redemonstrados depois pelos métodos clássicos. Isto não é em si surpreendente, já que a ANS é uma extensão conservadora da teoria dos conjuntos: todo teorema da teoria IST cujo enunciado é clássico já é um teorema da teoria ZFC. Este fato -a existência de uma demonstração clássica alternativa- combinado com a sensação de retrocesso que têm muitos matemáticos com relação a recorrer aos infinitesimais, sobre os quais a matemática teve tantas dificuldades para lidar, faz com que freqüentemente sua construção seja julgada como de pouca utilidade. Os que praticam a ANS rechaçam estas objeções. Eles insistem na mudança de visão que oportuniza a ANS, nas intuições e modelizações que ela pode fornecer, mais adaptada, segundo eles, com o mundo real do que aquelas relacionadas com a análise clássica. A uma visão do conjunto dos números reais como uma entidade homogênea, eles opõem a visão não standard que põe ao centro do sistema numérico uma distinção entre ordens de grandeza, refletindo a diversidade de escalas utilizadas na ciência atual e os limites necessariamente nebulosos entre estas escalas. Eles também insistem no potencial que oferece a ANS por meio dos infinitesimais em termos de modelizações discretas para muitas áreas de aplicação. Para eles, estes ganhos justificam que a ANS seja plenamente reconhecida.
No ensino também têm sido feitas diversas tentativas de desenvolver abordagens não standard para o ensino da análise elementar, baseadas na simplificação da construção de Robinson como as de Keisler (1976) ou de Heinle y Kleinberg (1979), ou inspiradas na abordagem axiomática de Nelson (Deledicq y Diener, 1989). Mas, como frisou Hodgson (1994) na síntese dos trabalhos que apresentou no congresso ICME -7 em Quebec, nenhuma destas construções inovadoras tem conseguido se impor de forma duradoura no ensino. A situação marginal da ANS sem dúvida não é estranha, mas sim o fato que, caso se queira fazer um uso produtivo da análise não standard, não basta introduzir a linguagem dos infinitesimais, deve-se aprender a manipular novos conceitos e definições, deve-se familiarizar-se com novas formas de raciocínio, construir novas referências e intuições, desenvolver novos métodos de controle.
Esta vinheta ilustra finalmente dois fenômenos frequentes na história das ciências e da matemática:
- o fato que a integração a teorias matemáticas rigorosas de ideias intuitivas pode não se tornar viável, até que, depois de anos ou mesmo séculos, devido a outros avanços científicos, estas intuições se revelem fecundas. Este foi o caso da ideia de infinitesimal, graças ao desenvolvimento da lógica matemática no século XX, mas também à ideia intuitiva de limite, que esteve na base da análise standard no século XIX, como salientado no início desta vinheta;
- também o fato de várias teorias sobre um mesmo aspecto da realidade poderem coexistir oferecendo perspectivas frutíferas e complementares para dar sentido e melhor trabalhar tal aspecto. Este é bem o caso da análise standard e da análise não standard, duas formas diferentes mas complementares de abordar o campo das funções e da análise, e de pensar suas conexões com o mundo real.
Gostaríamos de salientar que a construção aqui apresentada, a da ANS, não é a única possível para dar um status matemático para os infinitesimais. Diversas tentativas se sucederam ao longo da história (veja Borovik e Katz, 2012). A análise infinitesimal suave, desenvolvida a partir das ideias de F.W.Lawvere na teoria das categorias, é, por exemplo, uma outra construção recente: um infinitesimal aí é definido como um número não nulo cujo quadrado é nulo (ver Bell, 2008).
Referências:
Bell, J.L. (2008). A primer of infinitesimal analysis, 2nd edition. Cambridge : Cambridge University Press.
Borovik, B. & Katz, M. (2012) Who Gave you the Cauchy-Weierstrass Tale? The Dual History of Rigorous Calculus. Foundations of Science 17, no. 3, 245-276.
Berkeley, G. (1734). The Analyst. http://www.maths.tcd.ie/pub/HistMath/People/Berkeley/Analyst/
Benoît, E., Callot, J.L., Diener, F., & Diener. M. (1981). Chasse au canard. Collectanea Mathematica, 32.1, 38-74.
http://collectanea.ub.edu/index.php/Collectanea/article/view/3537/4216
Deledicq A., & Diener, M. (1989). Leçons de calcul infinitésimal. Collection U. Paris : Armand Colin.
Diener, M., & Diener, F. (Eds.). (1995). Non standard analysis in practice. Berlin : Springer Verlag.
Henle, J.M., & Kleinberg, E.M. (1979). Infinitesimal Calculus. Cambridge : MIT Press.
Hodgson, B. (1994). Le calcul infinitésimal. In, D.F. Robitaille, D.H. Wheeler et C. Kieran (Eds.), Choix de conférence du 7e Congrès international sur l’enseignement des mathématiques (ICME-7), pp. 157-170. Québec : Presses de l’Université Laval.
Document.
Keisler, H.J. (1976). Elementary calculus : An infinitesimal approach. Boston : Prindle, Weber & Schmidt.
Lakatos, I. (1978): Cauchy and the continuum: the significance of nonstandard analysis for the history and philosophy of mathematics. Math. Intelligencer 1, no. 3, 151–161 (paper originally presented in 1966).
Lutz, R. & Goze, M. (1982). Non standard analysis : a practical guide with applications. Springer Lecture Notes in Mathematics, vol. 881. Berlin : Springer.
Marquis de l’Hôpital, G.F.A. (1696). Analyse des infiniment petits pour l’intelligence des lignes courbes. Paris : Imprimerie Royale.
Nelson, E. (1977). Internal set Theory, a new approach to NSA, Bull. Amer. Math. Soc., vol. 83, no 6, 1165-1198.
Robinson, A. (1996). Non standard analysis. North Holland, Amsterdam.
Skolem, Th. (1934). Über die Nicht-charakterisierbarkeit der Zahlenreihe mittels endlich oder abzählbar unendlich vieler Aussagen mit ausschliesslich Zahlenvariablen. Fundam. Math. 23, 150-161
![]()
![]() O alcance deste cálculo é enorme: ele é conveniente tanto para curvas mecânicas como para geométricas; sinais de radicais lhes são indiferentes e frequentemente convenientes; estende-se a tantas indeterminadas quanto se queira; a comparação de infinitamente pequenos quaisquer lhe é igualmente fácil. Disto surge uma infinidade de descobertas surpreendentes sobre tangentes tanto a curvas como a retas, sobre questões envolvendo máximos e mínimos, pontos de inflexão e cúspides de curvas, curvas desenvolvíveis e cáusticas por reflexão ou por refração, etc. como se explica neste livro.
O alcance deste cálculo é enorme: ele é conveniente tanto para curvas mecânicas como para geométricas; sinais de radicais lhes são indiferentes e frequentemente convenientes; estende-se a tantas indeterminadas quanto se queira; a comparação de infinitamente pequenos quaisquer lhe é igualmente fácil. Disto surge uma infinidade de descobertas surpreendentes sobre tangentes tanto a curvas como a retas, sobre questões envolvendo máximos e mínimos, pontos de inflexão e cúspides de curvas, curvas desenvolvíveis e cáusticas por reflexão ou por refração, etc. como se explica neste livro.
![]() Axiomática de Zermelo-Fraenkel acrescida do axioma da escolha. (http://en.wikipedia.org/wiki/Zermelo–Fraenkel_set_theory).
Axiomática de Zermelo-Fraenkel acrescida do axioma da escolha. (http://en.wikipedia.org/wiki/Zermelo–Fraenkel_set_theory).
![]() O axioma de idealização diz que, para toda relação binária
O axioma de idealização diz que, para toda relação binária ![]() clássica (isto é, que pode ser expressa sem recorrer-se ao predicado
clássica (isto é, que pode ser expressa sem recorrer-se ao predicado ![]() ), as duas proposições seguintes são equivalentes: (i) para todo conjunto standard finito
), as duas proposições seguintes são equivalentes: (i) para todo conjunto standard finito ![]() , existe
, existe ![]() tal que, para todo
tal que, para todo ![]() de
de ![]() , tem-se
, tem-se ![]() ; (ii) existe
; (ii) existe ![]() tal que, para todo
tal que, para todo ![]() standard,
standard, ![]() .
.
O axioma de standardização diz que, para toda propriedade ![]() e todo conjunto standard
e todo conjunto standard ![]() , existe uma parte standard
, existe uma parte standard ![]() de
de ![]() cujos elementos standards são precisamente os elementos de
cujos elementos standards são precisamente os elementos de ![]() que satisfazem
que satisfazem ![]() . Este axioma vale, seja
. Este axioma vale, seja ![]() uma propriedade clássica ou não.
uma propriedade clássica ou não.
O axioma de transferência diz que, para toda propriedade clássica ![]() ,
, ![]() é verdadeira para todo
é verdadeira para todo ![]() se e somente se
se e somente se ![]() é verdadeira para todo
é verdadeira para todo ![]() standard.
standard.
![]() Basta aplicar o axioma de transferências à propriedade
Basta aplicar o axioma de transferências à propriedade ![]() :
: ![]()
![]() No primeiro caso, aplicamos o axioma da idealização em
No primeiro caso, aplicamos o axioma da idealização em ![]() à relação binária
à relação binária ![]() ; no segundo caso, o aplicamos no conjunto infinito considerado à relação binária
; no segundo caso, o aplicamos no conjunto infinito considerado à relação binária ![]() .
.
![]() No quadro, todos os objetos
No quadro, todos os objetos ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() são supostos standard.
são supostos standard.
![]() Neste enunciado,
Neste enunciado, ![]() ,
, ![]() ,
, ![]() e
e ![]() são supostos standard.
são supostos standard.
Este post está disponível em: Inglês, Francês, Alemão, Espanhol, Árabe

 Português
Português 简体中文
简体中文  English
English  Français
Français  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer