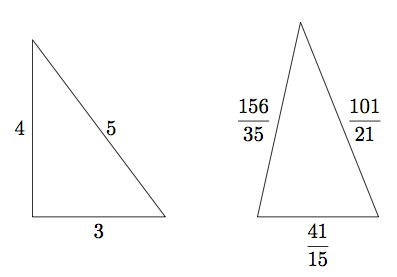 Vignette écrite par William Mc Callum.
Vignette écrite par William Mc Callum.
Si deux triangles ont la même aire et le même périmètre, sont-ils nécessairement isométriques? Il se trouve que la réponse est non. Par exemple, le triangle ayant des cotés de longueurs ![]() ,
, ![]() et
et ![]() a la même aire et le même périmètre que le triangle ayant des cotés de longueurs
a la même aire et le même périmètre que le triangle ayant des cotés de longueurs ![]() ,
, ![]() et
et ![]() .
.
Les deux triangles ont pour périmètre ![]() :
:
![]()
De façon surprenante, les deux triangles ont la même aire. Le triangle de droite a pour aire ![]() . Pour trouver l’ aire de l’ autre triangle, on utilise la Formule de Héron, selon laquelle l’ aire
. Pour trouver l’ aire de l’ autre triangle, on utilise la Formule de Héron, selon laquelle l’ aire ![]() d’ un triangle dont les cotés ont pour longueurs
d’ un triangle dont les cotés ont pour longueurs ![]() ,
, ![]() et
et ![]() , est donnée par
, est donnée par
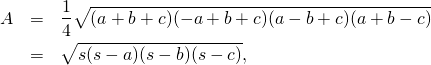
où ![]() est le demi-périmètre du triangle. Un rapide calcul utilisant cette formule montre que l’ aire du second triangle est également
est le demi-périmètre du triangle. Un rapide calcul utilisant cette formule montre que l’ aire du second triangle est également ![]() .
.
L’ espace des triangles
Comment trouve-t-on de tels exemples? Le secret est de trouver la bonne façon de représenter l’ espace de tous les triangles. Il y a de nombreuses façons de faire cela. Une façon est de représenter un triangle par le triplet ![]() des trois longueurs de ses cotés dans un certain ordre. Ainsi on représente un triangle par un point dans un espace à trois dimensions. Chaque point ne correspond pas à un triangle; par exemple, toutes les coordonnées doivent être positives. Pouvez-vous trouver d’ autres restrictions?
des trois longueurs de ses cotés dans un certain ordre. Ainsi on représente un triangle par un point dans un espace à trois dimensions. Chaque point ne correspond pas à un triangle; par exemple, toutes les coordonnées doivent être positives. Pouvez-vous trouver d’ autres restrictions?
Il y a une autre façon d’ attribuer des coordonnées dans l’ espace des triangles en utilisant des mesures d’ angles plutot que des longueurs. Chaque triangle a un cercle inscrit, et le rayon ![]() de ce cercle a une relation simple avec l’ aire
de ce cercle a une relation simple avec l’ aire ![]() et le demi-périmètre
et le demi-périmètre ![]() , à savoir
, à savoir
![]()
Pour voir cela, dessinons les perpendiculaires aux cotés du triangles passant par le centre du cercle, comme dans le dessin de droite de la Figure 2. Ces perpendiculaires forment les hauteurs de 3 petits triangles dont les bases sont les cotés du triangle de départ et le troisième sommet est le centre du cercle inscrit. L’ addition des aires de ces triangles nous donne ![]() .
.

Figure 2: Paramétrer l’ espace des triangles.
Cette équation nous montre que si deux triangles ont la même aire et le même demi-périmètre, alors les rayons de leurs cercles inscrits sont également les mêmes. Si nous cherchons de tels triangles nous allons donc les trouver parmi les triangles inscrits autour d’ un même cercle donné. Plutot que d’ utiliser des longueurs pour décrire ces triangles, nous allons utiliser les angles formés par les trois rayons au centre du cercle inscrit, comme indiqué sur le dessin de droite de la Figure 2.
Paramétrer les triangles d’ aire et périmètre constants
Dans l’ espace des triangles on peut trouver des courbes correspondant à une famille entière de triangles avec les mêmes valeurs pour ![]() et
et ![]() .
.
Tout d’ abord, on exprime ![]() en fonction des angles
en fonction des angles ![]() ,
, ![]() et
et ![]() et le rayon
et le rayon ![]() du cercle inscrit, comme suit. Les rayons et les droites passant par les sommets du triangle et le centre du cercle decoupent le triangle en six petits triangles rectangles. Puisque les droites passant par les sommets du triangle et le centre du cercle sont aussi les bissectrices des angles du triangle de départ, les six petits triangles rectangles forment trois paires de triangles isométriques. En prenant les longueurs des cotés adjacents aux angles droits dans chaque triangle rectangle et en additionnant, on obtient
du cercle inscrit, comme suit. Les rayons et les droites passant par les sommets du triangle et le centre du cercle decoupent le triangle en six petits triangles rectangles. Puisque les droites passant par les sommets du triangle et le centre du cercle sont aussi les bissectrices des angles du triangle de départ, les six petits triangles rectangles forment trois paires de triangles isométriques. En prenant les longueurs des cotés adjacents aux angles droits dans chaque triangle rectangle et en additionnant, on obtient
![]()
Cette équation et l’ égalité ![]() nous indiquent que si l’ aire
nous indiquent que si l’ aire ![]() et le demi-périmètre
et le demi-périmètre ![]() sont constants, alors la somme des tangentes suivantes l’ est aussi:
sont constants, alors la somme des tangentes suivantes l’ est aussi:
(1) ![]()
Ensuite, on transforme cette condition en une équation définissant une courbe dans le plan. Soit ![]() ,
, ![]() et
et ![]() . Puisque
. Puisque ![]() , on a
, on a
![]()
et
![]()
Ainsi, si ![]() est la constante
est la constante ![]() , l’ équation (1) devient, pour une valeur
, l’ équation (1) devient, pour une valeur ![]() donnée, l’ équation
donnée, l’ équation
(2) ![]()
(3) ![]()
Chaque triangle d’ aire ![]() et de demi-périmètre
et de demi-périmètre ![]() détermine un point sur cette courbe, et chaque point sur la courbe dans une certaine région du plan correspond à un triangle. La région correspondant aux angles satisfaisant la Figure 2, c’ est-à-dire les angles satisfaisant
détermine un point sur cette courbe, et chaque point sur la courbe dans une certaine région du plan correspond à un triangle. La région correspondant aux angles satisfaisant la Figure 2, c’ est-à-dire les angles satisfaisant ![]() et
et ![]() , qui correspondent à la région
, qui correspondent à la région ![]() ,
, ![]() et
et ![]() (puisque
(puisque ![]() ).
).
La figure suivante montre cette courbe dans le cas ![]() , la valeur correspondant aux triangles dont les cotés ont pour longueurs
, la valeur correspondant aux triangles dont les cotés ont pour longueurs ![]() ,
, ![]() et
et ![]() . Chaque point de la composante du quart supérieur droit du plan correspond à un triangle; les longueurs des cotés du triangle sont
. Chaque point de la composante du quart supérieur droit du plan correspond à un triangle; les longueurs des cotés du triangle sont ![]() ,
, ![]() et
et ![]() . En particulier, les points
. En particulier, les points ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() correspondent tous au triangle dont les cotés ont pour longueurs
correspondent tous au triangle dont les cotés ont pour longueurs ![]() ,
, ![]() et
et ![]() , avec les cotés choisis dans des ordres différents. Cette figure est interactive: essayez de déplacer le point
, avec les cotés choisis dans des ordres différents. Cette figure est interactive: essayez de déplacer le point ![]() ou de modifier les valeurs de l’aire ou du demi-périmètre!
ou de modifier les valeurs de l’aire ou du demi-périmètre!
Trouver des points sur la courbe
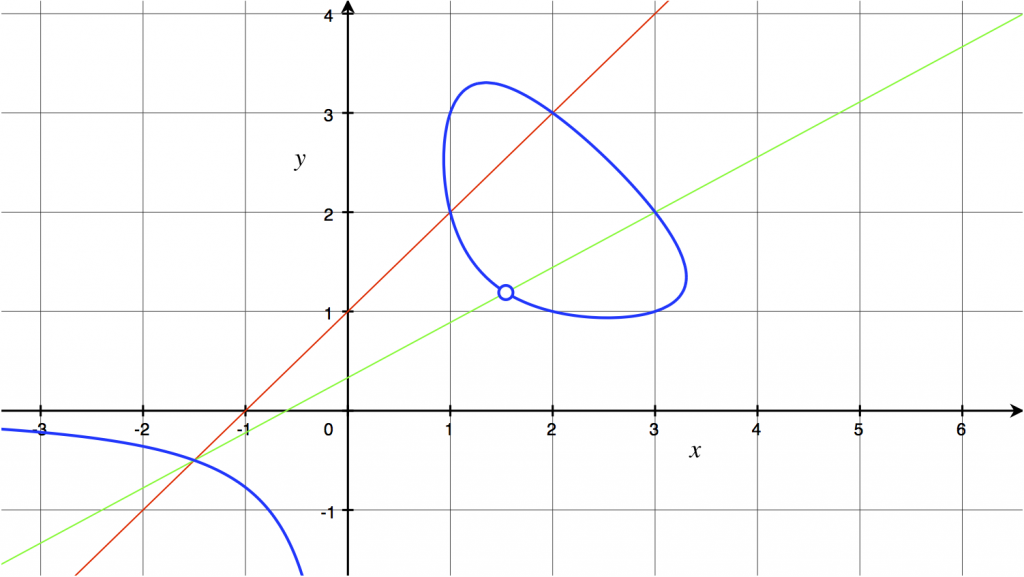
Figure 3: Courbe paramétrant les triangles de périmètre 12 et d'aire 6.
Puisque la courbe de la Figure 3 est définie par une équation polynomiale de degré ![]() , on peut y trouver des points en utilisant la méthode des tangentes et sécantes. Deux points sur la courbe déterminent une sécante qui intersecte la courbe en un autre point; trouver ce point consiste à résoudre une équation de degré
, on peut y trouver des points en utilisant la méthode des tangentes et sécantes. Deux points sur la courbe déterminent une sécante qui intersecte la courbe en un autre point; trouver ce point consiste à résoudre une équation de degré ![]() à une inconnue
à une inconnue ![]() , deux de ses racines étant connues. Puisque nous connaissons déjà
, deux de ses racines étant connues. Puisque nous connaissons déjà ![]() points de la courbe, il y a de nombreuses possibilités pour les sécantes, et déterminer plus de points produit encore plus de possibilités. En fait, la courbe a un nombre infini de points ayant des coordonnées rationnelles. Le procédé des deux sécantes illustré par la Figure 3 conduit au point de coordonnées
points de la courbe, il y a de nombreuses possibilités pour les sécantes, et déterminer plus de points produit encore plus de possibilités. En fait, la courbe a un nombre infini de points ayant des coordonnées rationnelles. Le procédé des deux sécantes illustré par la Figure 3 conduit au point de coordonnées ![]() ( indiqué par un cercle), qui correspond au triangle dont les cotés mesurent
( indiqué par un cercle), qui correspond au triangle dont les cotés mesurent ![]() ,
, ![]() et
et ![]() .
.
La méthode des sécantes fonctionne pour toute courbe elliptique (ces courbes ne sont pas des ellipses; elles sont appelées courbes elliptiques parce qu’ elles apparaissent dans l’ étude d’ une classe de fonctions complexes appelées fonctions elliptiques). La méthode des sécantes permet de définir une structure de groupe sur l’ ensemble des points rationnels d’ une courbe elliptique (c’ est-à-dire les points de la courbe ayant des coordonnées rationnelles).
L’ étude des courbes elliptiques est un sujet central en théorie des nombres, avec des applications dans les procédés cryptographiques des transactions financières sécurisées sur internet. Les courbes elliptiques ont joué un role central dans la preuve du dernier théorème de Fermat.
L’ histoire décrite dans cet article montre la remarquable unité des mathématiques, en commençant avec un problème accessible à des lycéens et terminant avec des recherches universitaires. En chemin nous avons été confrontés à une idée fondamentale des mathématiques modernes: Résoudre un problème à propos d’ un certain type d’ objet (les triangles dont l’ aire est ![]() et dont le périmètre est
et dont le périmètre est ![]() , par exemple) en situant l’ objet dans un espace plus général (l’ espace de tous les triangles) et en trouvant le bon moyen de paramétrer cet espace.
, par exemple) en situant l’ objet dans un espace plus général (l’ espace de tous les triangles) et en trouvant le bon moyen de paramétrer cet espace.
Ce post est disponible en: Chinois simplifié, Anglais, Allemand, Italien, Espagnol, Arabe, Khmère, Portugais - du Brésil

 Français
Français 简体中文
简体中文  English
English  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português