 Ursprüngliche Autorin ist Christiane Rousseau. (Übersetzt ins Deutsche von Reinhild Kokula, Universität Würzburg)
Ursprüngliche Autorin ist Christiane Rousseau. (Übersetzt ins Deutsche von Reinhild Kokula, Universität Würzburg)
Schon von Anfang an war Google „die“ Suchmaschine. Der Grund dafür ist die Überlegenheit seines Rangfolgenalgorithmus: der PageRank Algorithmus. Wegen der enormen Menge an Seiten im World-Wide-Web enden viele Suchanfragen tatsächlich mit Tausenden oder Millionen von Ergebnissen. Wenn diese nicht richtig geordnet sind, ist die Suche vielleicht gar keine Hilfe, weil man keine Millionen Einträge erkunden kann.
Wie funktioniert der PageRank Algorithmus?
Dies werden wir klären. Doch lassen Sie uns zunächst eine Suche mit Google starten. Am 4. Juni 2010 erhält man 16.300.000 Ergebnisse für Klein project, obwohl das Projekt gerade erst begonnen hat. An genau diesem Tag ist das erste Ergebnis
http://www.mathunion.org/icmi/other-activities/klein-project/introduction/
und nicht
http://www.kleinproject.org/
Die erste URL ist die URL einer Seite, die sich auf der Internetseite der International Mathematical Union befindet: http://www.mathunion.org.
Weil die International Mathematical Union eine wichtige Gesellschaft ist, erscheint ihre offizielle Internetseite als erstes Ergebnis, wenn man die Suchanfrage „International Mathematical Union“ startet. Weiterhin kommuniziert sie die Wichtigkeit all ihrer Seiten, von welchen eine
als erstes Ergebnis für die Suche Klein project erscheint.
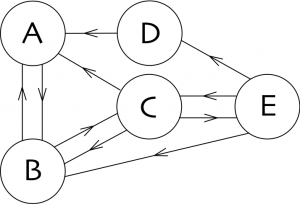
Um den Algorithmus zu erklären, modellieren wir das Internet als einen orientierten Graphen. Die Knoten sind die Seiten und die orientierten Kanten sind die Links zwischen Seiten. Wie gerade erklärt entspricht jede Seite einer anderen URL. Somit kann jede Webseite mehrere Seiten enthalten. Im Modell gibt es keinen Unterschied zwischen den einzelnen Unterseiten einer Webseite und der Titelseite, allerdings wird der Algorithmus mit großer Wahrscheinlichkeit die Titelseite einer wichtigen Webseite höher platzieren.
Ein einfaches Beispiel
 Betrachten wir das obige einfache Netz, das die fünf Seiten
Betrachten wir das obige einfache Netz, das die fünf Seiten ![]() ,
, ![]() ,
, ![]() ,
, ![]() und
und ![]() beschreibt. Dieses Netz enthält wenige Links. Wenn wir auf Seite
beschreibt. Dieses Netz enthält wenige Links. Wenn wir auf Seite ![]() sind, dann gibt es nur einen Link zu Seite
sind, dann gibt es nur einen Link zu Seite ![]() . Doch wenn man auf Seite
. Doch wenn man auf Seite ![]() ist, findet man drei Links und kann wählen, ob man zu Seite
ist, findet man drei Links und kann wählen, ob man zu Seite ![]() ,
, ![]() oder
oder ![]() fortfahren möchte. Beachten Sie, dass es mindestens einen Link von jeder Seite aus gibt.
fortfahren möchte. Beachten Sie, dass es mindestens einen Link von jeder Seite aus gibt.
Spielen wir ein Spiel, das lediglich ein zufälliger Spaziergang auf dem orientierten Graphen ist. Bei Beginn an einer Seite wählen wir bei jedem Schritt einen beliebigen Link von der Seite, auf der wir gerade sind, und folgen ihm. Wenn man in diesem Beispiel o.B.d.A. auf der Seite ![]() beginnen, so können wir zu
beginnen, so können wir zu ![]() oder zu
oder zu ![]() gehen, wobei jeder Fall eine Wahrscheinlichkeit von
gehen, wobei jeder Fall eine Wahrscheinlichkeit von ![]() aufweist. Wenn wir jedoch auf
aufweist. Wenn wir jedoch auf ![]() beginnen, so sind wir gezwungen, mit einer Wahrscheinlichkeit von
beginnen, so sind wir gezwungen, mit einer Wahrscheinlichkeit von ![]() nach
nach ![]() zu gehen. Wir wiederholen das Spiel.
zu gehen. Wir wiederholen das Spiel.
![Rendered by QuickLaTeX.com \[P=\begin{matrix} \begin{matrix} A & B & C & D & E \end{matrix} & \\ \left(\ \ \begin{matrix} 0 & \frac12 & \frac13 & 1 & 0 \\ 1 & 0 & \frac13 & 0 & \frac13 \\ 0 & \frac12 & 0 & 0 & \frac13 \\ 0 & 0 & 0 & 0 & \frac13 \\ 0 & 0 & \frac13 & 0 & 0 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix} \end{matrix}\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-042ffb6838118a58c7d9602fe9856d0b_l3.png)
Wir weisen darauf hin, dass die Summe der Einträge jeder Spalte gleich ![]() ist und dass alle Einträge größer oder gleich
ist und dass alle Einträge größer oder gleich ![]() sind. Matrizen mit diesen zwei Eigenschaften sind besondere Matrizen: Jede solche Matrix ist die Matrix eines Markow-Ketten-Prozesses und heißt deswegen die Markow-Übergangsmatrix. Sie besitzt immer
sind. Matrizen mit diesen zwei Eigenschaften sind besondere Matrizen: Jede solche Matrix ist die Matrix eines Markow-Ketten-Prozesses und heißt deswegen die Markow-Übergangsmatrix. Sie besitzt immer ![]() als Eigenwert und es gibt einen Eigenvektor zum Eigenwert
als Eigenwert und es gibt einen Eigenvektor zum Eigenwert ![]() , dessen Komponenten alle kleiner gleich
, dessen Komponenten alle kleiner gleich ![]() und größer gleich
und größer gleich ![]() sind, wobei ihre Summe
sind, wobei ihre Summe ![]() ergibt. Doch bevor wir uns die Definition von Eigenwert und Eigenvektor ins Gedächtnis rufen erkunden wir die Vorteile der Matrixrepräsentation des Netzgraphs.
ergibt. Doch bevor wir uns die Definition von Eigenwert und Eigenvektor ins Gedächtnis rufen erkunden wir die Vorteile der Matrixrepräsentation des Netzgraphs.
Betrachten wir eine zufällige Variable ![]() mit Werten in der Menge der Seiten
mit Werten in der Menge der Seiten ![]() , die
, die ![]() viele Seiten enthält (hier
viele Seiten enthält (hier ![]() ).
). ![]() repräsentiert die Seite, auf der wir nach n Schritten des zufälligen Spaziergangs gelandet sind. Wenn wir
repräsentiert die Seite, auf der wir nach n Schritten des zufälligen Spaziergangs gelandet sind. Wenn wir ![]() den Eintrag der Matrix
den Eintrag der Matrix ![]() nennen, der sich in der
nennen, der sich in der ![]() -ten Zeile und
-ten Zeile und ![]() -ten Spalte befindet, so ist folglich pij die bedingte Wahrscheinlichkeit, dass wir im
-ten Spalte befindet, so ist folglich pij die bedingte Wahrscheinlichkeit, dass wir im ![]() -ten Schritt auf der i-ten Seite landen, wenn wir im
-ten Schritt auf der i-ten Seite landen, wenn wir im ![]() -ten Schritt auf der
-ten Schritt auf der ![]() -ten Seite sind:
-ten Seite sind:
![]()
Beachten Sie, dass diese Wahrscheinlichkeit unabhängig von ![]() ist! Wir sagen, dass ein Markow-Kettenprozess keine Erinnerung an die Vergangenheit hat. Man sieht leicht, dass die Wahrscheinlichkeiten nach zwei Schritten in der Matrix
ist! Wir sagen, dass ein Markow-Kettenprozess keine Erinnerung an die Vergangenheit hat. Man sieht leicht, dass die Wahrscheinlichkeiten nach zwei Schritten in der Matrix ![]() summiert werden können.
summiert werden können.
Beweisen wir dies (wenn Sie wollen, können Sie den Beweis überspringen). Das Gesetz der totalen Wahrscheinlichkeit ergibt
![Rendered by QuickLaTeX.com \[\text{Prob}(X_{n+2}=i \mid X_n=j)=\sum_{k=1}^N\text{Prob}(X_{n+2}= i \;\text{and}\; X_{n+1}=k \mid X_n=j).\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-d218b844918839f2cc29f13a5c22a02d_l3.png)
Nach Definition der bedingten Wahrscheinlichkeit gilt
![Rendered by QuickLaTeX.com \[\text{Prob}(X_{n+2}=i \mid X_n=j)=\sum_{k=1}^N\frac{\text{Prob}(X_{n+2}= i \;\text{and}\; X_{n+1}=k \;\text{and}\; X_n=j)} {\text{Prob}(X_n=j)}.\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-5106f79e05a5ce44aba08836606f60c1_l3.png)
Wir nutzen einen altbekannten Trick und multiplizieren und dividieren mit derselben Menge:
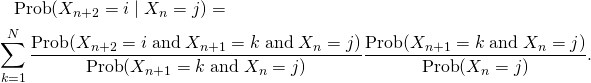
Der erste Quotient ist gleich
![]()
weil der Markow-Kettenprozess keine Erinnerung vor dem vorherigen Schritt hat. Daher gilt
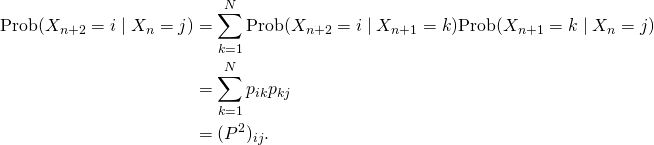
In unserem Beispiel folgt
![Rendered by QuickLaTeX.com \[P^2=\begin{matrix} \begin{matrix} A & B & C & D & E \end{matrix} & \\ \left(\ \ \begin{matrix}\frac12 & \frac16 & \frac16 & 0 & \frac{11}{18} \\ 0 & \frac23 & \frac49 & 1 & \frac19 \\ \frac12 & 0 & \frac5{18} & 0 & \frac16 \\ 0 & 0 & \frac19 & 0 & 0 \\ 0 & \frac16 & 0 & 0 & \frac19 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix} \end{matrix}\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-c815aee0d8d73d9494ae3dcdbf160507_l3.png)
Wenn man diese Idee wiederholt, wird klar, dass der Eintrag ![]() der Matrix
der Matrix ![]() die Wahrscheinlichkeit
die Wahrscheinlichkeit ![]() beschreibt. Zum Beispiel:
beschreibt. Zum Beispiel:
![Rendered by QuickLaTeX.com \[P^{32} =\begin{matrix} \begin{matrix} \:\:A \quad& \:\:B\quad & \:\:C \quad& \:\:D\quad &\:\: E \quad\end{matrix} & \\ \left(\ \ \begin{matrix} 0.293 & 0.293 & 0.293 & 0.293 & 0.293 \\ 0.390 & 0.390 & 0.390 & 0.390 & 0.390 \\ 0.220 & 0.220 & 0.220 & 0.220 & 0.220 \\ 0.024 & 0.024 & 0.024 & 0.024 & 0.024 \\ 0.073 & 0.073 & 0.073 & 0.073 & 0.073 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix}\end{matrix}\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-de62ad1480800013e6d29802e633ec19_l3.png)
Alle Spalten von ![]() sind identisch, wenn wir die Genauigkeit auf 3 Dezimalen festsetzen, und sie sind dieselben wie die Spalten von Pn, wenn
sind identisch, wenn wir die Genauigkeit auf 3 Dezimalen festsetzen, und sie sind dieselben wie die Spalten von Pn, wenn ![]() ist. Wenn wir eine höhere Genauigkeit wählen, so findet man auch eine Stabilisierung, aber für
ist. Wenn wir eine höhere Genauigkeit wählen, so findet man auch eine Stabilisierung, aber für ![]() größer als
größer als ![]() . Daher ist nach
. Daher ist nach ![]() Schritten, sofern
Schritten, sofern ![]() ausreichend groß ist, die Wahrscheinlichkeit, auf einer Seite zu sein, unabhängig von der Startposition!
ausreichend groß ist, die Wahrscheinlichkeit, auf einer Seite zu sein, unabhängig von der Startposition!
Betrachten wir zudem den Vektor
![]()
(![]() ist ein vertikaler Vektor und seine Transposition
ist ein vertikaler Vektor und seine Transposition ![]() ist ein horizontaler Vektor). Man kann leicht zeigen, dass
ist ein horizontaler Vektor). Man kann leicht zeigen, dass ![]() . Wenn wir die
. Wenn wir die ![]() -te Koordinate des Vektors
-te Koordinate des Vektors ![]() als die Wahrscheinlichkeit setzen, auf der Seite
als die Wahrscheinlichkeit setzen, auf der Seite ![]() zu einer gegebenen Zeit
zu einer gegebenen Zeit ![]() zu sein, und somit die Wahrscheinlichkeitsverteilung der Seiten zum Zeitpunkt
zu sein, und somit die Wahrscheinlichkeitsverteilung der Seiten zum Zeitpunkt ![]() ist, so ist sie auch die Wahrscheinlichkeitsverteilung zum Zeitpunkt
ist, so ist sie auch die Wahrscheinlichkeitsverteilung zum Zeitpunkt ![]() . Aus diesem Grund wird der Vektor
. Aus diesem Grund wird der Vektor ![]() auch als stabile Verteilung bezeichnet. Diese stabile Verteilung erlaubt es, die Seiten zu ordnen. In unserem Beispiel ordnen wir die Seiten als
auch als stabile Verteilung bezeichnet. Diese stabile Verteilung erlaubt es, die Seiten zu ordnen. In unserem Beispiel ordnen wir die Seiten als ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() und bestimmen
und bestimmen ![]() als die wichtigste Seite.
als die wichtigste Seite.
Der allgemeine Fall
Der allgemeine Fall kann genau wie unser Beispiel behandelt werden. Wir stellen das Netz als einen orientierten Graphen dar, in dem die ![]() Knoten die
Knoten die ![]() Seiten des Netzes repräsentieren und die orientierten Kanten die Links zwischen den Seiten sind. Wir fassen den Graphen in einer N
Seiten des Netzes repräsentieren und die orientierten Kanten die Links zwischen den Seiten sind. Wir fassen den Graphen in einer N![]() -Matrix zusammen,
-Matrix zusammen, ![]() , wobei die
, wobei die ![]() -Spalte die
-Spalte die ![]() -te Startseite beschreibt und die
-te Startseite beschreibt und die ![]() -Zeile die
-Zeile die ![]() -te Zielseite. In unserem Beispiel haben wir einen Vektor gefunden, der erfüllt. Dieser Vektor ist ein Eigenvektor zum Eigenwert
-te Zielseite. In unserem Beispiel haben wir einen Vektor gefunden, der erfüllt. Dieser Vektor ist ein Eigenvektor zum Eigenwert ![]() . Rufen wir uns die Definition von Eigenwert und Eigenvektor in den Sinn.
. Rufen wir uns die Definition von Eigenwert und Eigenvektor in den Sinn.
Definition. Sei P eine N x N-Matrix. Eine Zahl ![]() ist ein Eigenwert von
ist ein Eigenwert von ![]() , falls es einen nichttrivialen Vektor
, falls es einen nichttrivialen Vektor ![]() gibt, sodass
gibt, sodass ![]() . Einen solchen Vektor
. Einen solchen Vektor ![]() nennt man einen Eigenvektor von
nennt man einen Eigenvektor von ![]() .
.
Wir erinnern uns ebenfalls an die Methode zur Ermittlung von Eigenwerten und Eigenvektoren.
Proposition Sei ![]() Eine
Eine ![]() Matrix. Die Eigenwerte von
Matrix. Die Eigenwerte von ![]() sind die Wurzeln des charakteristischen Poynoms
sind die Wurzeln des charakteristischen Poynoms ![]() , wobei
, wobei ![]() die
die ![]() -Einheitsmatrix ist. Die Eigenvektoren zu einem Eigenwert
-Einheitsmatrix ist. Die Eigenvektoren zu einem Eigenwert ![]() sind die nichttrivialen Lösungen des homogenen linearen Gleichungssystems
sind die nichttrivialen Lösungen des homogenen linearen Gleichungssystems ![]() .
.
Der folgende tiefergehende Satz von Frobenius garantiert, dass wir für eine mit einem Netzgraphen verknüpfte Matrix immer eine feste Lösung finden.
Satz (Satz von Frobenius) Wir betrachten eine ![]() Markow-Übergangsmatrix
Markow-Übergangsmatrix ![]() (wobei
(wobei ![]() für alle
für alle ![]() , und die Summe der Einträge jeder Spalte gleich
, und die Summe der Einträge jeder Spalte gleich ![]() ist, also
ist, also ![]() ).
).
Dann gilt:
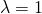 ist ein Eigenwert von
ist ein Eigenwert von 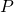 .
.- Für jeden Eigenwert
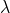 von P gilt
von P gilt  .
. - Es gibt einen Eigenvektor
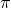 zum Eigenwert
zum Eigenwert 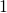 , dessen Koordinaten alle größer oder gleich Null sind. O.B.d.A. können wir annehmen, dass die Summe seiner Koordinaten
, dessen Koordinaten alle größer oder gleich Null sind. O.B.d.A. können wir annehmen, dass die Summe seiner Koordinaten 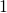 ist.
ist.
Nun ist es Zeit, die Stärke dieses Satzes zu bewundern. Aus diesem Grund werden wir die vereinfachte Hypothese stellen, dass die Matrix ![]() eine Basis
eine Basis ![]() an Eigenvektoren hat und wir nehmen an, dass
an Eigenvektoren hat und wir nehmen an, dass ![]() der Vektor
der Vektor ![]() des Satzes von Frobenius ist. Für jedes
des Satzes von Frobenius ist. Für jedes ![]() existiert ein
existiert ein ![]() derart, dass
derart, dass ![]() . Betrachten wir einen beliebigen nichttrivialen Vektor
. Betrachten wir einen beliebigen nichttrivialen Vektor ![]() mit
mit ![]() , wobei
, wobei ![]() und
und ![]() . Wir zerlegen
. Wir zerlegen ![]() in die Basis
in die Basis ![]() :
:
![Rendered by QuickLaTeX.com \[X=\sum_{i=1}^N a_iv_i.\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-75c52ea84c4a0aa148f3aa2977bdb8be_l3.png)
Ein technischer Beweis, den wir überspringen werden, erlaubt es zu zeigen, dass ![]() . Berechnen wir nun
. Berechnen wir nun ![]() :
:
![Rendered by QuickLaTeX.com \[PX= \sum_{i=1}^Na_i Pv_i= \sum_{i=1}^n a_i\lambda_iv_i,\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-3f5f58d838bdce8623400f20b0c3eb55_l3.png)
Da ![]() ein Eigenvektor zum Eigenwert
ein Eigenvektor zum Eigenwert ![]() ist. Und bei Iteration erhalten wir
ist. Und bei Iteration erhalten wir
![Rendered by QuickLaTeX.com \[P^nX= \sum_{i=1}^n a_i\lambda_i^nv_i.\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-42c385cba649519613da2a81cae3b1bb_l3.png)
Falls alle ![]() für
für ![]() die Bedingung
die Bedingung ![]() erfüllen, dann gilt
erfüllen, dann gilt
![]()
Genau das passiert in unserem Beispiel!
Beachten Sie jedoch, dass der Satz nicht garantiert, dass eine beliebige Matrix ![]() , die die Hypothese des Satzes erfüllt, diese Eigenschaft aufweisen wird. Beschreiben wir die möglichen Symptome und das Gegenmittel.
, die die Hypothese des Satzes erfüllt, diese Eigenschaft aufweisen wird. Beschreiben wir die möglichen Symptome und das Gegenmittel.
Mögliche Symptome.
- Der Eigenwert
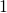 kann eine mehrfache Wurzel des charakteristischen Polynoms
kann eine mehrfache Wurzel des charakteristischen Polynoms  sein.
sein. - Die Matrix
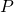 kann andere Eigenwerte
kann andere Eigenwerte 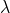 haben als
haben als 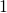 , die mit Modulo gleich
, die mit Modulo gleich 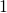 sind.
sind.
Was tun wir in diesem Fall?
Wir nennen eine Markow-Übergangsmatrix ohne Symptome eine reguläre Markow-Übergangsmatrix, nämlich:
Definition. Eine Markow-Übergangsmatrix ist regulär, falls
- Der Eigenwert
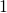 eine einfache Wurzel des charakteristischen Polynoms
eine einfache Wurzel des charakteristischen Polynoms  ist.
ist. - Alle anderen Eigenwerte
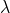 von
von 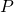 außer
außer 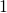 haben Modulos kleiner als
haben Modulos kleiner als 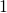 . Bedenken Sie, dass die meisten Matrizen
. Bedenken Sie, dass die meisten Matrizen 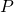 regulär sind. Wenn also die Markow-Übergangsmatrix eines Netzes nicht regulär ist, so lautet die Strategie, die Matrix leicht umzuformen, sodass sie regulär wird.
regulär sind. Wenn also die Markow-Übergangsmatrix eines Netzes nicht regulär ist, so lautet die Strategie, die Matrix leicht umzuformen, sodass sie regulär wird.
Gegenmittel. Wir betrachten die ![]() Matrix
Matrix ![]() mit
mit ![]() für alle
für alle ![]() . Wir ersetzen die Matrix
. Wir ersetzen die Matrix ![]() des Netzes mit der Matrix
des Netzes mit der Matrix
(1) ![]()
für kleine ![]() (der Wert
(der Wert ![]() wird von Google benutzt). Bedenken Sie, dass die Matrix
wird von Google benutzt). Bedenken Sie, dass die Matrix ![]() noch nichtnegative Einträge besitzt und dass die Summe der Einträge jeder Spalte immer noch gleich
noch nichtnegative Einträge besitzt und dass die Summe der Einträge jeder Spalte immer noch gleich ![]() ist, wodurch es noch eine Markow-Übergangsmatrix ist. Der folgende Satz sichert, dass ein solches
ist, wodurch es noch eine Markow-Übergangsmatrix ist. Der folgende Satz sichert, dass ein solches ![]() existiert, für das wir die Symptome kuriert haben.
existiert, für das wir die Symptome kuriert haben.
Satz Für eine beliebige Markow-Übergangsmatrix ![]() gibt es immer ein beliebig kleines, positives
gibt es immer ein beliebig kleines, positives ![]() , sodass die Matrix
, sodass die Matrix ![]() regulär ist. Sei
regulär ist. Sei ![]() der Eigenvektor von
der Eigenvektor von ![]() zur Matrix normiert, sodass die Summe seiner Koordinaten 1 sei. Für die Matrix und einen nichttrivialen Vektor
zur Matrix normiert, sodass die Summe seiner Koordinaten 1 sei. Für die Matrix und einen nichttrivialen Vektor ![]() , wobei
, wobei ![]() mit
mit ![]() und
und ![]() , gilt
, gilt
(2) ![]()
Zusammenhang zum Banachschen Fixpunktsatz
Eine andere (anstehende) Vignette behandelt den Banachschen Fixpunktsatz. Der obige Satz kann als Spezialisierung dessen angesehen werden. Sie können diesen Teil überspringen, wenn Sie die andere Vignette nicht gelesen haben. In der Tat gilt:
Satz Sei ![]() eine reguläre Markow-Transformationsmatrix. Betrachten wir
eine reguläre Markow-Transformationsmatrix. Betrachten wir ![]() , mit angemessenem Abstand
, mit angemessenem Abstand ![]() zwischen den Punkten (dieser Abstand ist abhängig von
zwischen den Punkten (dieser Abstand ist abhängig von ![]() ). Auf
). Auf ![]() betrachten wir den linearen Operator
betrachten wir den linearen Operator ![]() , definiert durch
, definiert durch ![]() . Der Operator
. Der Operator ![]() ist eine Kontraktion auf
ist eine Kontraktion auf ![]() und es existiert ein
und es existiert ein ![]() , sodass für alle
, sodass für alle ![]() gilt
gilt
![]()
Dann existiert ein eindeutiger Vektor ![]() derart, dass
derart, dass ![]() .
.
Zudem können wir anhand eines beliebigen gegebenen ![]() die Folge
die Folge ![]() durch Induktion definieren, wobei
durch Induktion definieren, wobei ![]() . Dann gilt
. Dann gilt ![]() .
.
Definition des Abstands ![]() . Die Definition des Abstands
. Die Definition des Abstands ![]() ist recht geschickt und kann übersprungen werden. Hier wird er nur der Vollständigkeit zuliebe eingefügt und für den Leser, der auf die Details drängt. Wir beschränken uns auf den Fall, in dem die Matrix
ist recht geschickt und kann übersprungen werden. Hier wird er nur der Vollständigkeit zuliebe eingefügt und für den Leser, der auf die Details drängt. Wir beschränken uns auf den Fall, in dem die Matrix ![]() diagonalisierbar ist. Sei
diagonalisierbar ist. Sei ![]() eine Basis aus Eigenvektoren. Vektoren
eine Basis aus Eigenvektoren. Vektoren ![]() können mithilfe der Basis
können mithilfe der Basis ![]() geschrieben werden:
geschrieben werden:
![Rendered by QuickLaTeX.com \[X=\sum_{i=1}^N a_iv_i, \quad Y=\sum_{i=1}^N b_iv_i,\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-e4878c51bc88f673f3e86656255bb8ef_l3.png)
Wobei ![]() . Dann definieren wir
. Dann definieren wir
![Rendered by QuickLaTeX.com \[d(X,Y)=\sum_{i=1}^n |a_i-b_i|.\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-ca97409e4ea4eb245c8b0400d97b8332_l3.png)
Mit diesem Anstand ist ![]() ein abgeschlossener metrischer Raum, was bedeutet, dass alle Cauchyfolgen konvergieren.
ein abgeschlossener metrischer Raum, was bedeutet, dass alle Cauchyfolgen konvergieren.
Dieser Satz sichert nicht nur die Existenz eines ![]() , sondern liefert eine Methode, um es als den Grenzwert der Folge
, sondern liefert eine Methode, um es als den Grenzwert der Folge ![]() zu konstruieren. Wir haben eine Illustration dieser Konvergenz in unserem Beispiel gesehen. Tatsächlich ist die
zu konstruieren. Wir haben eine Illustration dieser Konvergenz in unserem Beispiel gesehen. Tatsächlich ist die ![]() -te Spalte von
-te Spalte von ![]() der Vektor
der Vektor ![]() , wobei
, wobei ![]() der
der ![]() -te Vektor der kanonischen Basis ist. In unserem Beispiel hätten wir den Vektor
-te Vektor der kanonischen Basis ist. In unserem Beispiel hätten wir den Vektor ![]() auch direkt finden können durch Lösung des Systems
auch direkt finden können durch Lösung des Systems ![]() mit der Matrix
mit der Matrix
![Rendered by QuickLaTeX.com \[I-P= \left(\begin{matrix} 1 &- \frac12 & -\frac13 & -1 & 0 \\ -1 & 1 & -\frac13 & 0 & -\frac13 \\ 0 & -\frac12 & 1 & 0 & -\frac13 \\ 0 & 0 & 0 & 1 & -\frac13 \\ 0 & 0 & -\frac13 & 0 & 1 \end{matrix}\right).\]](http://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-05e0ba5931bfe376391bdb5e783a74b2_l3.png)
Wir hätten herausgefunden, dass alle Lösungen der Form ![]() sind für
sind für ![]() . Die Lösung, deren Summe der Koordinaten
. Die Lösung, deren Summe der Koordinaten ![]() ergibt, ist folglich
ergibt, ist folglich ![]() mit
mit
![]()
Praktische Berechnung der festen Verteilung
Wir haben die einfache Idee identifiziert, die dem Algorithmus unterliegt. Allerdings ist es nicht so trivial, die feste Verteilung ![]() , also einen Eigenvektor zum Eigenwert
, also einen Eigenvektor zum Eigenwert ![]() für die Matrix
für die Matrix ![]() in (1), zu finden, wenn die Matrix Milliarden Zeilen und Spalten hat: sowohl die Rechenzeit als auch der benötigte Speicherplatz erweisen sich als große Herausforderungen. Die normale Methode der Gauß-Elimination ist in diesem Fall unbrauchbar, wegen der Größe der Berechnung und weil man dabei durch kleine Koeffizienten teilen muss. Ein effektiverer Algorithmus nutzt die Eigenschaft (2) (siehe [LM]). Dies bildet den Zusammenhang zur bevorstehenden Vignette über den Banachschen Fixpunktsatz, die klarstellen wird, dass der Beweis des Banachschen Fixpunktsatzes einen Algorithmus liefert, um den Fixpunkt zu konstruieren.
in (1), zu finden, wenn die Matrix Milliarden Zeilen und Spalten hat: sowohl die Rechenzeit als auch der benötigte Speicherplatz erweisen sich als große Herausforderungen. Die normale Methode der Gauß-Elimination ist in diesem Fall unbrauchbar, wegen der Größe der Berechnung und weil man dabei durch kleine Koeffizienten teilen muss. Ein effektiverer Algorithmus nutzt die Eigenschaft (2) (siehe [LM]). Dies bildet den Zusammenhang zur bevorstehenden Vignette über den Banachschen Fixpunktsatz, die klarstellen wird, dass der Beweis des Banachschen Fixpunktsatzes einen Algorithmus liefert, um den Fixpunkt zu konstruieren.
Tatsächlich beginnen wir mit ![]() derart, dass
derart, dass
![]()
und wir müssen ![]() berechnen. Normalerweise liefert
berechnen. Normalerweise liefert ![]() für
für ![]() zwischen
zwischen ![]() und
und ![]() eine relativ gute Approximation von
eine relativ gute Approximation von ![]() . Durch Induktion berechnen wir
. Durch Induktion berechnen wir ![]() . Sogar solche Berechnungen sind recht lang. Tatsächlich hat die Matrix
. Sogar solche Berechnungen sind recht lang. Tatsächlich hat die Matrix ![]() in (1) aufgrund der Berechnung keine Nulleinträge. Andererseits sind die meisten Einträge von
in (1) aufgrund der Berechnung keine Nulleinträge. Andererseits sind die meisten Einträge von ![]() gleich Null. Also müssen wir die Berechnung zerlegen um dies auszunutzen, nämlich durch
gleich Null. Also müssen wir die Berechnung zerlegen um dies auszunutzen, nämlich durch
![]()
Aufgrund dieser speziellen Form von ![]() prüft man leicht nach, dass
prüft man leicht nach, dass ![]() , wenn
, wenn ![]() ein Vektor ist, deren Einträge summiert
ein Vektor ist, deren Einträge summiert ![]() ergeben. Folglich genügt es, die folgende Folge zu berechnen:
ergeben. Folglich genügt es, die folgende Folge zu berechnen:
![]()
Schlussfolgerung
Wir haben hiermit den öffentlichen Teil von Googles PageRank Algorithmus präsentiert. Man kann bereits mit einfachen Netzen experimentieren und das Ranking seiner eigenen Seite verbessern, indem man zusätzliche interne und externe Links an optimalen Stellen einfügt. Manche private kultiviertere Teile werden weiterhin entwickelt. Manche von ihnen bestehen daraus, die „neutrale“ Matrix Q aus (1) mit einer Matrix zu ersetzen, die den Geschmack des Internetsurfers reflektiert. Andere sichern, dass das Ranking nicht zu sehr sensibel auf Manipulationen reagiert, die von denjenigen vorgenommen werden, die das Ranking ihrer Seiten zu verbessern suchen.
Als generelle Schlussfolgerung können wir festhalten: Eine einfache, clevere Idee hat zu einem immensen Durchbruch in der Effizienz von Suchmaschinen geführt und zur Geburt eines kommerziellen Empires. Auch wenn die Implementation selbst eine rechenbetonte Tat ist, benötigte die zugrundeliegende Idee „elementare“ Mathematik, nämlich die lineare Algebra und die Wahrscheinlichkeitstheorie. Diese mathematischen Standardtools, vor allem die Diagonalisierung von Matrizen, konnten ihre volle Kraft entfalten, weil sie außerhalb ihres „normalen“ Kontexts genutzt wurden. Außerdem haben wir die vereinenden Ideen innerhalb der Wissenschaft hervorgehoben, mit denen der Banachsche Fixpunktsatz Anwendungen so weit entfernt seines Ursprungs findet.
Bibliographie
[E] M. Eisermann, Comment Google classe les pages webb, http://images.math.cnrs.fr/Comment-Google-classe-les-pages.html, 2009.
[LM] A. N. Langville and C. D. Meyer, A Survey of Eigenvector Methods
for Web Information Retrieval, SIAM Review, Volume 47, Issue 1,
(2005), pp. 135–161.
[RS] C. Rousseau and Y. Saint-Aubin, Mathematics and
technology, SUMAT Series, Springer-Verlag, 2008 (A French version of the book exists, published in the same series.)
Andere Sprachen: Englisch, Französisch, Italienisch, Spanisch, Arabisch, Khmer

 Deutsch
Deutsch 简体中文
简体中文  English
English  Français
Français  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português