 Originalautorin ist Michèle Artigue. (Übersetzt ins Deutsche von Reinhild Kokula, Universität Würzburg)
Originalautorin ist Michèle Artigue. (Übersetzt ins Deutsche von Reinhild Kokula, Universität Würzburg)
Infinitesimale spielten eine wichtige Rolle in der Entstehung und Entwicklung der Differential- und Integralanalysis. Die offensichtliche Leistungsfähigkeit der Analysis verhinderte allerdings nicht die wiederkehrenden heftigen Debatten über die Natur dieser Objekte und die Zulässigkeit ihrer Nutzung. Gegen Ende des 19. Jahrhunderts, als die Konstruktion der reellen Zahlen aus den ganzen Zahlen und die moderne Definition des Grenzwertkonzepts eine solide Grundlage für Differential- und Integralanalysis lieferten, wurden Infinitesimale und die damit zusammenhängende Metaphysik zurückgewiesen und ihr Nutzen wurde als synonym zu vergangenen und wenig präzisen Praktiken angesehen. Allerdings wurde die Sprache der Infinitesimalen weiterhin benutzt, z.B. in der Physik und sogar in der Mathematik. Sie verschwand nie vollends aus dem informellen Diskurs und dem heuristischen Denken einer Vielzahl von Forschern.
Ist diese Sprache also wirklich inkompatibel mit der mathematischen Präzision? Welche interessanten und speziellen Dinge hat sie zu bieten, die ihr Fortweilen erklären? Nichtstandard-Analysis wurde im 20. Jahrhundert entwickelt und lieferte Antworten auf diese Fragen und gab den Infinitesimalen die Möglichkeit, sich zu rächen.
Vom infinitesimalen Kalkül zur Nichtstandard-Analysis
Im Vorwort zur ersten Abhandlung über infinitesimale Analysis, die 1696 veröffentlicht wurde, prahlte der Autor, der Marquis de l’Hôpital, über die Leistungsfähigkeit und die Einfachheit des Calculus, die die Infinitesimalen ermöglichen![]() :
:

Abbildung 1: Titelseite und Auszug aus dem Vorwort der Abhandlung des Marquis de l’Hôpital
Allerdings kamen recht schnell Debatten über Infinitesimale und ihren Nutzen auf. In einem bekannten, im Jahre 1734 veröffentlichten Aufsatz, The Analyst, entwickelt George Berkely eine heftige Kritik an der Nutzung von Infinitesimalen oder infinitesimalen Zuwächsen im Differentialkalkulus, und Jean Le Rond d’Alembert versucht sich in der 1751 veröffentlichten L’Encyclopédie Méthodique von ihnen zu befreien, indem er sich auf die intuitive Idee des Grenzwerts stützt. Mit der Wende zum 20. Jahrhunderts schien dies mit der Entwicklung der modernen Analysis erreicht. Allerdings wird der Logiker Abraham Robinson ein halbes Jahrhundert später Infinitesimale und damit verbundene Praktiken wieder nutzbar machen.
Abraham Robinson zeigt tatsächlich auf, dass die Sprache der Infinitesimalen vollkommen mit der mathematischen Präzision vereinbar ist. Der Logiker Thoralf Skolem hatte bereits 1934 gezeigt, dass die Menge, die man durch aufeinanderfolgende Addition von Einheiten zu 0 erhält, nicht das einzige Model zu Peanos Axiomen der Arithmetik ist und dass daher weitere Modelle existieren, die aus diesem Grund nicht-standard genannt werden. Im Jahre 1961 zeigte Abraham Robinson anhand einer Konstruktion, die auf Ultra-Produkten basiert, dass es ein Nichtstandardmodell des Körpers der reellen Zahlen gibt, der die Zahlen „unendlich groß“ und „unendlich klein“ enthält. Dies war die Geburtsstunde der Nichtstandardanalysis (NSA). Dann, im Jahre 1977, fand Edward Nelson heraus, wie man die NSA axiomatisieren kann. Um dies zu tun, addierte er ein einstelliges Prädikatssymbol ![]() , das ausdrückt, dass ein Objekt
, das ausdrückt, dass ein Objekt ![]() Standard zur Sprache der Gruppentheorie ist und drei Axiome zu den ZFC-Axiomen
Standard zur Sprache der Gruppentheorie ist und drei Axiome zu den ZFC-Axiomen![]() der Gruppentheorie: die Axiome der Idealisierung, der Standardisierung und des Transfers
der Gruppentheorie: die Axiome der Idealisierung, der Standardisierung und des Transfers![]() , was es einfacher machte, die NSA zu manipulieren. In dieser Vignette stützen wir uns auf diese Axiomatisierung, genannt IGT (Interne Gruppentheorie).
, was es einfacher machte, die NSA zu manipulieren. In dieser Vignette stützen wir uns auf diese Axiomatisierung, genannt IGT (Interne Gruppentheorie).
Diese drei Axiome ziehen wichtige Folgen mit sich. Aus dem Transferaxiom zum Beispiel folgt, dass zwei Standardmengen E1 und E2 genau dann gleich sind, wenn sie dieselben kanonischen Elemente haben![]() . Aus demselben Axiom folgt auch, dass – falls es ein
. Aus demselben Axiom folgt auch, dass – falls es ein ![]() gibt mit Beschaffenheit
gibt mit Beschaffenheit ![]() (also eine Beschaffenheit, die ausgedrückt werden kann ohne die Eigenschaft st), dann notwendigerweise auch ein standardisiertes
(also eine Beschaffenheit, die ausgedrückt werden kann ohne die Eigenschaft st), dann notwendigerweise auch ein standardisiertes ![]() existiert, das dies erfüllt. Zahlen und alltägliche Objekte, denen wir in der Mathematik oft begegnen: Die Zahlen
existiert, das dies erfüllt. Zahlen und alltägliche Objekte, denen wir in der Mathematik oft begegnen: Die Zahlen ![]() ,
, ![]() , trigonometrische und exponentielle Funktionen gehören in diese Kategorie und sind daher Standardobjekte, wie die leere Menge, die Menge
, trigonometrische und exponentielle Funktionen gehören in diese Kategorie und sind daher Standardobjekte, wie die leere Menge, die Menge ![]() der natürlichen Zahlen und die Menge
der natürlichen Zahlen und die Menge ![]() der reellen Zahlen.
der reellen Zahlen.
Allerdings ist es nicht notwendig, das es nur Standardelemente gibt, wenn man eine Standardmenge hat. Tatsächlich folgt aus dem Axiom der Idealisierung, dass in ![]() eine Zahl existiert, die größer als alle Standardzahlen ist und daher notwendigerweise nicht-standard ist. Allgemeiner kann man mithilfe dieses Axioms einfach zeigen, dass jede beliebige unendliche Menge Nicht-Standardelemente enthält
eine Zahl existiert, die größer als alle Standardzahlen ist und daher notwendigerweise nicht-standard ist. Allgemeiner kann man mithilfe dieses Axioms einfach zeigen, dass jede beliebige unendliche Menge Nicht-Standardelemente enthält![]() .
. ![]() und
und ![]() sind daher Standardmengen, die sowohl Standard- als auch Nicht-Standardelemente enthalten. Wie können wir sie repräsentieren?
sind daher Standardmengen, die sowohl Standard- als auch Nicht-Standardelemente enthalten. Wie können wir sie repräsentieren?
In ![]() kommen alle Standardzahlen zuerst und sind den Nicht-Standardzahlen vorrangig. In
kommen alle Standardzahlen zuerst und sind den Nicht-Standardzahlen vorrangig. In ![]() ist die Situation etwas komplizierter. Man kann zwischen drei Kategorien der reellen Zahlen unterscheiden, anhand ihrer Größe:
ist die Situation etwas komplizierter. Man kann zwischen drei Kategorien der reellen Zahlen unterscheiden, anhand ihrer Größe:
- Die reellen Zahlen, die sehr klein oder Infinitesimale sind (positiv oder negativ), die, deren Absolutwert kleiner als jede positive reelle Standardzahl ist,
- Die reellen Zahlen, die sehr groß oder unendlich groß sind (positiv oder negativ), die, deren Absolutwerte größer ist als jede positive reelle Standardzahl ist,
- Und, dazwischen, die reellen Zahlen, die sozusagen eine menschliche Größe haben und oft auch die erkennbaren Zahlen genannt werden.
Ist eine Zahl infinitesimal oder erkennbar, so ist sie begrenzt. Ist eine reelle Zahl unendlich groß, so ist ihr Inverses infinitesimal, und beide sind nicht-standard. Erkennbare reelle Zahlen können Standard oder Standard sein. Betrachten wir zum Beispiel die reelle Zahl ![]() ; addieren wir dazu ein infinitesimales
; addieren wir dazu ein infinitesimales ![]() ungleich
ungleich ![]() , so ist die erhaltene Zahl
, so ist die erhaltene Zahl ![]() ebenfalls erkennbar, allerdings nicht-standard und unendlich nahe bei
ebenfalls erkennbar, allerdings nicht-standard und unendlich nahe bei ![]() . Um jede reelle Standardzahl existiert folglich eine Wolke von unendlich nahen reellen Nicht-Standardzahlen. Um diese Situation zu schildern führen wir eine neue Relation ein. Man besagt
. Um jede reelle Standardzahl existiert folglich eine Wolke von unendlich nahen reellen Nicht-Standardzahlen. Um diese Situation zu schildern führen wir eine neue Relation ein. Man besagt ![]() als unendlich nahe bei
als unendlich nahe bei ![]() , falls
, falls ![]() ein Infinitesimal ist, was als
ein Infinitesimal ist, was als ![]() notiert wird. Die Ansammlung der reellen Zahlen, die unendlich nahe bei einer gegebenen reellen Zahl liegen, nennt man Halo oder Mondring. Infinitesimale sind der Mondring von
notiert wird. Die Ansammlung der reellen Zahlen, die unendlich nahe bei einer gegebenen reellen Zahl liegen, nennt man Halo oder Mondring. Infinitesimale sind der Mondring von ![]() und jede erkennbare reelle Zahl gehört zum Mondkreis einer einzigartigen reellen Standardzahl, die sein Standardteil genannt wird. Die reelle Nicht-Standardlinie wird wie in Abbildung 2 repräsentiert, mit einer verschwommenen Grenze zwischen reellen Zahlen, die erkennbar sind und solchen, die unendlich groß sind, da die Ansammlung der erkennbaren reellen Zahlen kein Maximum hat und die Ansammlung der unendlich großen Zahlen kein Minimum hat.
und jede erkennbare reelle Zahl gehört zum Mondkreis einer einzigartigen reellen Standardzahl, die sein Standardteil genannt wird. Die reelle Nicht-Standardlinie wird wie in Abbildung 2 repräsentiert, mit einer verschwommenen Grenze zwischen reellen Zahlen, die erkennbar sind und solchen, die unendlich groß sind, da die Ansammlung der erkennbaren reellen Zahlen kein Maximum hat und die Ansammlung der unendlich großen Zahlen kein Minimum hat.

Abbildung 2: Repräsentation der reellen Nicht-Standardlinie
Rechenregeln, die die verschiedenen Größen der Zahlen berücksichtigen, erweitern die der Arithmetik. Notiert man die Infinitesimalen als ![]() , die Erkennbaren als
, die Erkennbaren als ![]() und die unendlich Großen als
und die unendlich Großen als ![]() , so erhält man zum Beispiel:
, so erhält man zum Beispiel: ![]() ,
, ![]() ,
, ![]() und
und ![]() , und wir laden den Leser dieser Vignette dazu ein, die folgenden Tabellen wo möglich zu vervollständigen:
, und wir laden den Leser dieser Vignette dazu ein, die folgenden Tabellen wo möglich zu vervollständigen:

Die Menge der reellen Zahlen erfüllt noch immer Archimedes Axiom: sind ![]() und
und ![]() positive reellen Zahlen wie
positive reellen Zahlen wie ![]() , dann existiert eine ganze Zahl
, dann existiert eine ganze Zahl ![]() , sodass
, sodass ![]() , aber falls natürlich
, aber falls natürlich ![]() infinitesimal ist und
infinitesimal ist und ![]() nicht, so wird
nicht, so wird ![]() unendlich groß.
unendlich groß.
The set of real numbers still verifies the Archimede’s axiom: if ![]() and
and ![]() are positive real numbers such as
are positive real numbers such as ![]() , there exists an integer
, there exists an integer ![]() such as
such as ![]() , but of course if
, but of course if ![]() is an infinitesimal and
is an infinitesimal and ![]() is not,
is not, ![]() will be infinitely big.
will be infinitely big.
NSA und grundlegende Auffassungen der Analysis
Innerhalb des Rahmens der NSA haben grundlegende Auffassungen der mathematischen Analysis, zum Beispiel Grenzwerte, Stetigkeit, Differenzierbarkeit und Integrierbarkeit eine einfache Formalisierung für Standardobjekte, wie die folgende Tabelle zeigt![]() :
:
Within the framework of NSA, basic notions of mathematical analysis: limits, continuity, differentiability and integrability have very simple formalisations for standard objects, as shown in the table below![]() :
:

Diese einfachen Formalisierungen ohne Alternation der Quantoren und der unterliegenden These erlaubt vereinfachte Beweise vieler klassischer Sätze. Folgend stellen wir als Illustration einen Nicht-Standardbeweis für den Zwischenwertsatz auf.
|
Zwischenwertsatz:
Beweis: O.B.d.A. nehmen wir an, dass |
ANS erlaubt außerdem die Rechtfertigung der Technik des Zerteilens in infinitesimale Stücke, die stets noch außerhalb der mathematischen Gemeinschaft zur Berechnung von Flächen, Volumen, Trägheitsmomenten, Gravitationszentren, etc. verwendet wird, oder für die Modellierung von Situationen anhand von Differentialgleichungen. Das untenstehende Beispiel ist eine sehr einfache Illustration davon.
Berechnung des Volumens einer Kugel
Sei ![]() eine Kugel mit Radius
eine Kugel mit Radius ![]() . Man schneidet die Kugel in Stücke mit der infinitesimalen Dicke
. Man schneidet die Kugel in Stücke mit der infinitesimalen Dicke ![]() . Das Volumen
. Das Volumen ![]() des Stückes auf der Höhe
des Stückes auf der Höhe ![]() ist ungefähr das eines Zylinders von
ist ungefähr das eines Zylinders von ![]() und Höhe
und Höhe ![]() .
.
![]()
Von hier erhält man durch Summierung
![]()
![]()
und zuletzt ![]() .
.
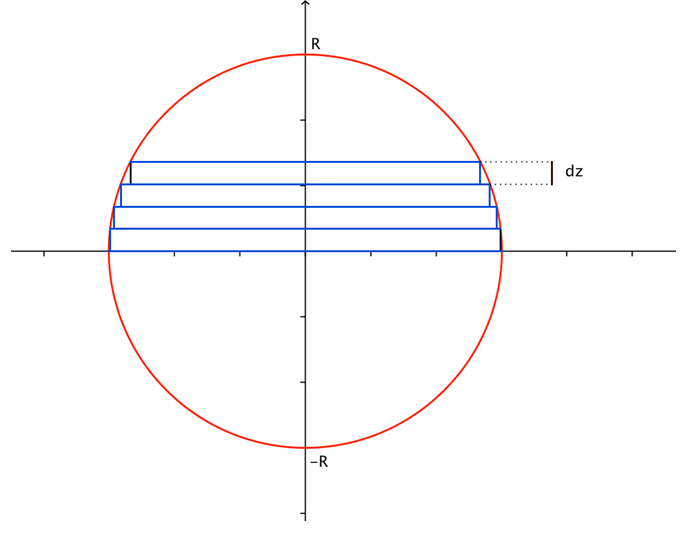
Volumen einer Kugel
Die Summe der Volumina der infinitesimalen Zylinder ist tatsächlich die Cauchysumme, die zur infinitesimalen Aufteilung des Schrittes ![]() auf das Intervall
auf das Intervall ![]() für die Flächenfunktion
für die Flächenfunktion ![]() . Betrachten wir die Nicht-Standarddefinition des Integrals für stetige Funktionen, so ist der Standardteil dieser Summe also gleich dem Integral
. Betrachten wir die Nicht-Standarddefinition des Integrals für stetige Funktionen, so ist der Standardteil dieser Summe also gleich dem Integral ![]() .
.
Allerdings resultiert die Tatsache, dass dieses Integral korrekt das Volumen der Kugel wiedergibt, aus der Tatsache, dass die für ![]() vorgeschlagene Approximation ein Äquivalent des Volumens des Stückes ist, und nicht nur eine unendlich naheliegende. Es wäre nicht der Fall, wenn die selbe Approximation durch zylindrische Stücke genutzt würde, um zum Beispiel die Fläche der Kugel zu berechnen.
vorgeschlagene Approximation ein Äquivalent des Volumens des Stückes ist, und nicht nur eine unendlich naheliegende. Es wäre nicht der Fall, wenn die selbe Approximation durch zylindrische Stücke genutzt würde, um zum Beispiel die Fläche der Kugel zu berechnen.
Die Notwendigkeit, wachsam zu bleiben
Allerdings muss man bei der Manipulation von Nicht-Standardobjekten wachsam bleiben. Zum Beispiel erhält man bei der Erweiterung der obigen Stetigkeitsdefinition auf jede reelle Zahl und Funktion – Standard oder Nicht-Standard – eine neue Auffassung; eine ![]() -Stetigkeit an einem Punkt, die nicht unbedingt unserer Vorstellung von stetigen Funktionen entspricht. Die Treppenfunktion, zum Beispiel, die auf den negativen reellen Zahlen den Wert
-Stetigkeit an einem Punkt, die nicht unbedingt unserer Vorstellung von stetigen Funktionen entspricht. Die Treppenfunktion, zum Beispiel, die auf den negativen reellen Zahlen den Wert ![]() annimmt und auf den positiven reellen Zahlen und
annimmt und auf den positiven reellen Zahlen und ![]() den Wert
den Wert ![]() annimmt, wobei
annimmt, wobei ![]() sich infinitesimal von
sich infinitesimal von ![]() unterscheidet, ist
unterscheidet, ist ![]() -stetig bei
-stetig bei ![]() , da das Bild einer jeden positiven Infinitesimalen das Infinitesimal
, da das Bild einer jeden positiven Infinitesimalen das Infinitesimal ![]() ist. Umgekehrt ist die quadratische Funktion nicht
ist. Umgekehrt ist die quadratische Funktion nicht ![]() -stetig in
-stetig in ![]() , wenn
, wenn ![]() unendlich groß ist, da
unendlich groß ist, da ![]() nicht unendlich nahe bei
nicht unendlich nahe bei ![]() ist. Tatsächlich ist für eine Standardfunktion die S-Stetigkeit an einem beliebigen Punkt in
ist. Tatsächlich ist für eine Standardfunktion die S-Stetigkeit an einem beliebigen Punkt in ![]() gleich der gleichmäßigen Stetigkeit über
gleich der gleichmäßigen Stetigkeit über ![]() . Die Berechnungen, die wir gerade für die quadratische Funktion durchgeführt haben, sind ein sehr einfacher Beweis dafür, dass die quadratischen Funktionen zwar stetig über
. Die Berechnungen, die wir gerade für die quadratische Funktion durchgeführt haben, sind ein sehr einfacher Beweis dafür, dass die quadratischen Funktionen zwar stetig über ![]() sind, aber nicht gleichmäßig stetig über
sind, aber nicht gleichmäßig stetig über ![]() .
.
Wenn man also bei der Behandlung der NSA Induktion anwendet, muss man wachsam bleiben. In ihrer alltäglichen Form gilt sie für klassische Eigenschaften; dies ist eine Folge des Transferaxioms, aber nicht weiter. Betrachten Sie die folgende Begründung, die oft als Paradoxon präsentiert wird:
Sei ![]() die Eigenschaft, «Standard zu sein».
die Eigenschaft, «Standard zu sein». ![]() ist wahr und für jede ganze Zahl
ist wahr und für jede ganze Zahl ![]() ist
ist ![]() wahr, falls
wahr, falls ![]() wahr ist. Dann ist also für jedes
wahr ist. Dann ist also für jedes ![]()
![]() wahr, somit sind alle ganzen Zahlen Standard.
wahr, somit sind alle ganzen Zahlen Standard.
|
Sei
|
Das Prinzip der Induktion wird hier auf eine nicht-klassische Aussage angewandt, die mit der Eigenschaft ![]() beschrieben wird. Diese Begründung ist tatsächlich gar kein Paradoxon, sondern einfach nicht gültig. Man nämlich beweisen, dass in der NSA für nicht-klassische Eigenschaften
beschrieben wird. Diese Begründung ist tatsächlich gar kein Paradoxon, sondern einfach nicht gültig. Man nämlich beweisen, dass in der NSA für nicht-klassische Eigenschaften ![]() nur das reduzierte Prinzip der Induktion gültig ist: Ist
nur das reduzierte Prinzip der Induktion gültig ist: Ist ![]() wahr und impliziert
wahr und impliziert ![]() für eine beliebige ganze Zahl
für eine beliebige ganze Zahl ![]()
![]() , so ist
, so ist ![]() wahr für alle Standardzahlen.
wahr für alle Standardzahlen.
Das Potenzial von NSA: Eine noch umstrittene Frage
Wie oben gezeigt, arbeitet die NSA infinitesimale Zahlen, Berechnungsmöglichkeiten und Intuitionen, die sie zeigen, auf, doch der Preis dafür ist Arbeit und Wachsamkeit. Also was können wir mit NSA gewinnen? Diese Frage wird in der mathematischen Gemeinschaft noch diskutiert, so zum Beispiel im Terence Tao Blog, den wir während der Vorbereitung dieser Vignette besucht haben. NSA wird mit Erfolg in einem breiten Spektrum von mathematischen Disziplin verwendet: Topologie, Wahrscheinlichkeit, dynamische Systeme… Sie hat zum Beispiel interessante Modellierungen in der Automatik, Ökologie, Ökonomie unterstützt. In Frankreich wurde auf die Initiative es Mathematikers Georges Reeb hin eine Nicht-Standard-Gemeinschaft in den späten Siebzigern entwickelt, die neue Resultate in vielen Bereichen erlangte (cf. (Lutz et Goze, 1982), (Diener & Diener, 1995)). Unter den Bekanntesten ist die Entdeckung einer bestimmten Flugbahn, genannt die „Entenbahn“, in langsam-schnellen Vektorfeldern in zwei und drei Dimensionen. Wir präsentieren das folgende untenstehende Beispiel, ohne genauer auf die technischen Details dieser Nicht-Standardabhandlung einzugehen, wobei wir dieselben Differentialgleichungen wie (Benoît et al., 1981) nutzen. Der Leser, der mit Differentialgleichungen nicht vertraut ist, kann diesen Teil überspringen.
Die „Enten“-Bahnen
Wir betrachten die Differentialgleichung ![]() , wobei
, wobei ![]() und
und ![]() . Eine klassische Betrachtung dieser Gleichung zeigt, dass, falls
. Eine klassische Betrachtung dieser Gleichung zeigt, dass, falls ![]() , die Gleichung eine eindeutige periodische Lösung hat, was ein attraktiver Grenzwertzyklus ist. Für
, die Gleichung eine eindeutige periodische Lösung hat, was ein attraktiver Grenzwertzyklus ist. Für ![]() verschwindet diese periodische Lösung und für
verschwindet diese periodische Lösung und für ![]() existiert ein attraktiver stationärer Status
existiert ein attraktiver stationärer Status ![]() . Das Phänomen der Entenbahnen hat in der Dynamik der Gleichung Vorrang vor dieser Bifurkation, auch bekannt als die Hopf-Bifurkation. Es wurde für sehr kleine
. Das Phänomen der Entenbahnen hat in der Dynamik der Gleichung Vorrang vor dieser Bifurkation, auch bekannt als die Hopf-Bifurkation. Es wurde für sehr kleine ![]() beobachtet und für Werte, die nahe bei
beobachtet und für Werte, die nahe bei ![]() sind. Eine Nicht-Standardmodellierung hat es uns erlaubt, dieses Phänomen zu identifizieren und die Bedingungen für ihr Auftreten zu charakterisieren.
sind. Eine Nicht-Standardmodellierung hat es uns erlaubt, dieses Phänomen zu identifizieren und die Bedingungen für ihr Auftreten zu charakterisieren.
Zunächst wandeln wir die Differentialgleichung zweiten Grades in ein System ersten Grades um. Dies kann man auf zwei verschiedene Weisen tun; zunächst stellt man ![]() als
als ![]() dar; dies ist eine spezielle Umwandlung, die für die Untersuchung dieses Gleichungstyps als Liénard-Typ bekannt ist. Die zweite Weise ist
dar; dies ist eine spezielle Umwandlung, die für die Untersuchung dieses Gleichungstyps als Liénard-Typ bekannt ist. Die zweite Weise ist ![]() umzuwandeln; die klassische Weise, eine Gleichung in ein System umzuwandeln. Somit erhält man die folgenden zwei Systeme, in denen
umzuwandeln; die klassische Weise, eine Gleichung in ein System umzuwandeln. Somit erhält man die folgenden zwei Systeme, in denen ![]() eine unendlich große Zahl ist:
eine unendlich große Zahl ist:
![]()
![]()
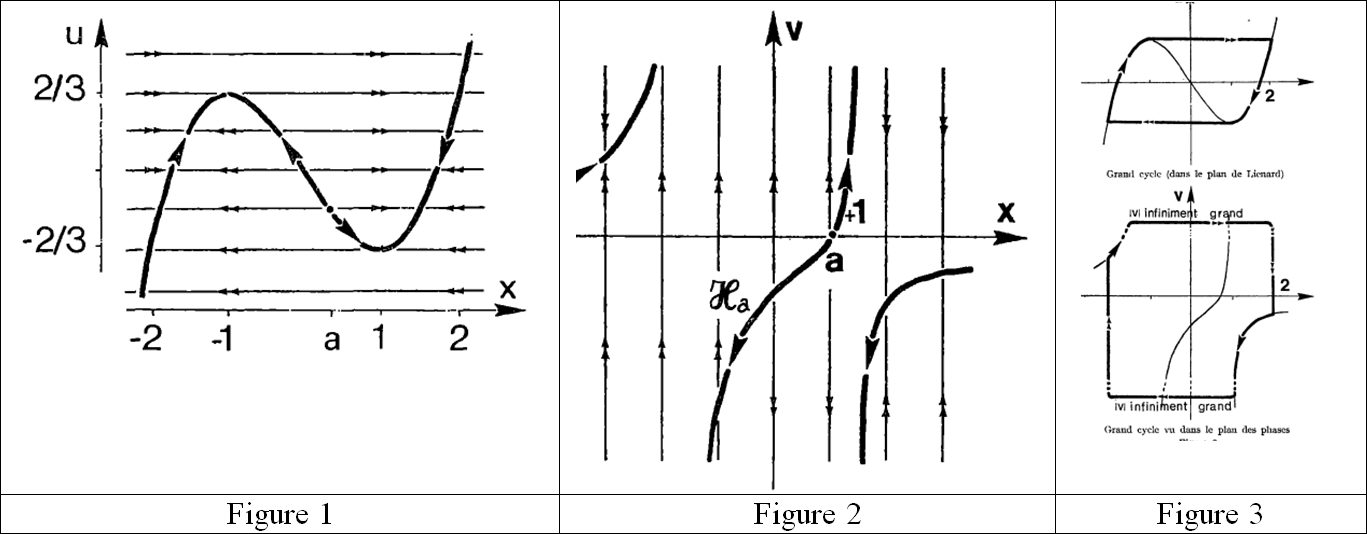
Die damit verbundenen Vektorfelder in den jeweiligen Ebenen ![]() und
und ![]() sind in Figur 1 und 2 dargestellt und aus (Benoît et al., 1981) kopiert. Sie sind langsam-schnelle Vektorfelder. Zum Beispiel ist das Feld in der
sind in Figur 1 und 2 dargestellt und aus (Benoît et al., 1981) kopiert. Sie sind langsam-schnelle Vektorfelder. Zum Beispiel ist das Feld in der ![]() -Ebene oder der Liénard-Ebene fast horizontal außerhalb dem Mondkreis de kubischen
-Ebene oder der Liénard-Ebene fast horizontal außerhalb dem Mondkreis de kubischen ![]() mit der Gleichung
mit der Gleichung ![]() , dessen steigende Teile attraktiv sin aufgrund der Richtung der horizontalen Pfeile, während der fallende Teil abstoßend ist. Die Doppelpfeile sollen daran erinnern, dass diese Teile, fast horizontal, sich mit einer unendlich großen Geschwindigkeit bewegen. Durch Kombination von Werkzeugen aus der Standard- und Nicht-Standardanalysis, vor allem Änderung der Skalierung durch Makroskope oder unendlich große Verhältnisse in einer Richtung der Ebenen
, dessen steigende Teile attraktiv sin aufgrund der Richtung der horizontalen Pfeile, während der fallende Teil abstoßend ist. Die Doppelpfeile sollen daran erinnern, dass diese Teile, fast horizontal, sich mit einer unendlich großen Geschwindigkeit bewegen. Durch Kombination von Werkzeugen aus der Standard- und Nicht-Standardanalysis, vor allem Änderung der Skalierung durch Makroskope oder unendlich große Verhältnisse in einer Richtung der Ebenen ![]() und
und ![]() , kann man zeigen, dass ein eindeutiger, attraktiver Kreislauf (Figur 3) existiert, wenn
, kann man zeigen, dass ein eindeutiger, attraktiver Kreislauf (Figur 3) existiert, wenn ![]() , aber nicht im Mondkreis von
, aber nicht im Mondkreis von ![]() . In der
. In der ![]() -Ebene, zum Beispiel, würde ein Teilchen, das sich entlang dieses Kreises bewegt – zum Beispiel beim Punkt M außerhalb des Mondkreises von C startet –, sich fast horizontal diesem Mondkreis annähern und sich mit unendlicher Geschwindigkeit bewegen, dann bei
-Ebene, zum Beispiel, würde ein Teilchen, das sich entlang dieses Kreises bewegt – zum Beispiel beim Punkt M außerhalb des Mondkreises von C startet –, sich fast horizontal diesem Mondkreis annähern und sich mit unendlicher Geschwindigkeit bewegen, dann bei ![]() entlang reisen, in seinem Mondkreis bleiben mit einer nennenswerten Geschwindigkeit von
entlang reisen, in seinem Mondkreis bleiben mit einer nennenswerten Geschwindigkeit von ![]() und schließlich im Mondkreis seines lokalen Minimums
und schließlich im Mondkreis seines lokalen Minimums ![]() ankommen. Dann schlägt es wieder eine fast horizontale Flugbahn ein, bis es wieder den Mondkreis von C erreicht und folgt diese Kurve dann bis zum Mondkreis des lokalen Maximums
ankommen. Dann schlägt es wieder eine fast horizontale Flugbahn ein, bis es wieder den Mondkreis von C erreicht und folgt diese Kurve dann bis zum Mondkreis des lokalen Maximums ![]() ; dann beginnt es wieder mit einer fast horizontalen Bewegung…
; dann beginnt es wieder mit einer fast horizontalen Bewegung…
Ist ![]() , so ist die Situation etwas komplexer, da einzelne Zweige der Kurve
, so ist die Situation etwas komplexer, da einzelne Zweige der Kurve ![]() , die zu
, die zu ![]() in der
in der ![]() -Ebene gehören, sich unendlich annähern. Daraus folgt, dass für die
-Ebene gehören, sich unendlich annähern. Daraus folgt, dass für die ![]() -Ebene eine Lösung, die
-Ebene eine Lösung, die ![]() bis in den Mondkreis von
bis in den Mondkreis von ![]() gefolgt ist, für manche Werte von
gefolgt ist, für manche Werte von ![]() ein Stück weit den abstoßenden Teil von
ein Stück weit den abstoßenden Teil von ![]() folgen können, bevor sie fast horizontal werden und den Mondkreis des attraktiven Teils von
folgen können, bevor sie fast horizontal werden und den Mondkreis des attraktiven Teils von ![]() erreichen (Abbildung 4).
erreichen (Abbildung 4).
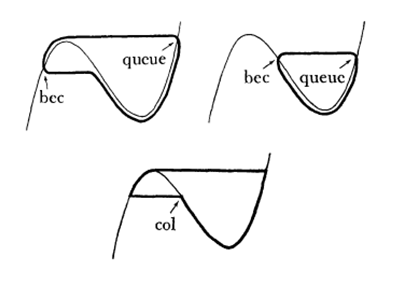
Abbildung 4 Morphologie der Entenbahnen
Aufgrund ihrer Form haben Forscher die damit verbundenen Kreisläufe als Entenbahnen bezeichnet. Zum Beispiel zeigten sie, dass es für eine beliebige reelle Zahl ![]() zwischen
zwischen ![]() und
und ![]() ein Wert existiert, für den es eine Entenbahn gibt, dessen Schnabel die Abszisse
ein Wert existiert, für den es eine Entenbahn gibt, dessen Schnabel die Abszisse ![]() hat. Ohne die Unterstützung der NSA-Modellierung würde die Existenz solcher Bahnen womöglich ignoriert bleiben. Um sie tatsächlich zu beobachten, ist es nicht ausreichend, ein kleines
hat. Ohne die Unterstützung der NSA-Modellierung würde die Existenz solcher Bahnen womöglich ignoriert bleiben. Um sie tatsächlich zu beobachten, ist es nicht ausreichend, ein kleines ![]() und ein
und ein ![]() nahe
nahe ![]() zu haben; es wurde bewiesen, dass es notwendig ist, dass
zu haben; es wurde bewiesen, dass es notwendig ist, dass ![]() sehr nahe bei
sehr nahe bei ![]() ist, genauer, dass das Verhältnis
ist, genauer, dass das Verhältnis ![]() ein Infinitesimal ist. Über das rein mathematische Interesse hinaus hat die Existenz von Entenbahnen für Systeme von Differentialgleichungen in zwei und drei Dimensionen Anwendungen in außermathematischen Bereichen.
ein Infinitesimal ist. Über das rein mathematische Interesse hinaus hat die Existenz von Entenbahnen für Systeme von Differentialgleichungen in zwei und drei Dimensionen Anwendungen in außermathematischen Bereichen.
Wir müssen allerdings betonen, dass die neuen Ergebnisse, die NSA-Forscher gewonnen haben, später oft auch mit Standardmethoden bewiesen wurden. Dies ist an sich nicht überraschend, da die IGT eine erhaltende Erweiterung von ZFC ist: Ein beliebiger Satz der IGT, der eine klassische Formulierung hat, ist auch ein Satz der ZFC. Kombiniert man dies mit der Tatsache, dass viele Mathematiker das Gefühl haben, dass die Nutzung der Infinitesimalen eine Regression ist, von der die Mathematiker nur mit viel Schwierigkeit fortgekommen waren, führt diese Situation oft dazu, dass man die Konstruktion der NSA als von geringem Nutzen ansieht. Diejenigen, die NSA benutzen, lehnen diese Einwände ab. Die betonen den Sichtwechsel, den die NSA vermittelt, die Intuitionen und Modellierungen, die sie ermöglicht und die mehr an die Realität der Welt angepasst werden können als Standardpraktiken. Einer Vision der reellen Zahlen als homogene Einheit setzen sie die Nicht-Standardvision entgegen, die im Herzen des numerischen Systems zwischen der Größe der Zahlen unterscheidet und somit die Verschiedenheit der Zahlenskalen und die verschwommenen Grenzen zwischen ihnen reflektieren, die Wissenschaftler zurzeit betrachten. Sie bestehen auf das Potential, dass die NSA durch Infinitesimale im Sinne der diskreten Modellierung in vielen Bereichen Anwendung findet. Ihrer Ansicht nach gebührt der NSA aufgrund diesen Potentials volle Anerkennung.
Auch in der mathematischen Erziehung wurden verschiedene Versuche gestartet, Nicht-Standardzugänge zur Lehre der Analysis zu finden. Diese basierten entweder auf Robinsons Konstruktion (wie von Kleiser, 1976, vorgeschlagen; und Henle & Kleinberg, 1979), oder wurden von Nelsons axiomatischem Zugang inspiriert (Deledicq & Diener, 1989). Wie allerdings von Hogdson (1994) in der Synthese über diese Beziehungen am ICME-7 Congress in Québec hervorgehoben wurde, waren keine dieser innovativen Konstruktionen nachhaltig. Der Randgruppenstatus der NSA hilft in dieser Hinsicht nach sicherlich nicht zu einem höheren Ansehen, aber auch die Tatsache, dass man lernen muss, neue Ideen und Definitionen zu manipulieren, sich mit neuen Argumentationsmodi vertrauen, neue Bezüge und Intuitionen schaffen und neue Kontrollmöglichkeiten entwickeln muss, um die Nicht-Standardanalysis effizient nutzen zu können und die Nutzung von Infinitesimalen nicht ausreichend ist.
Schlussendlich illustriert diese Vignette zwei in der Geschichte der Wissenschaft und Mathematik häufig auftretende Phänomene:
- Die Tatsache, dass die Integration intuitiver Ideen in gut begründete Theorien erst Jahrzehnte oder Jahrhunderte, nachdem sie als fruchtbar bewiesen wurden, integriert werden aufgrund anderer wissenschaftlicher Fortschritte. Dies war der Fall für die intuitive Idee der Infinitesimalen dank der Entwicklung der mathematischen Logik im 20. Jahrhundert, aber auch für die intuitive Idee des Grenzwertes, der die Grundlage der Standardanalysis im 19. Jahrhunderts ist, wie wir uns zu Beginn dieser Vignette ins Gedächtnis gerufen haben;
- Die Tatsache, dass einige theoretische Überlegungen über das gleiche Gebiet der Wirklichkeit koexistieren können, was fruchtbare und komplementäre Perspektiven ermöglicht, Sinn aus dieser Wirklichkeit zu schaffen und an ihr zu arbeiten. Dies ist der Fall für Standard- und Nicht-Standardanalysis – zwei unterschiedliche, aber komplementäre Weisen, das Gebiet der Funktionen und Analysis anzugehen und über ihre Bezüge zur realen Welt zu denken.
Wir möchten zum Schluss hervorheben, dass die hier präsentierte Konstruktion, die der NSA, nicht die einzige ist, um Infinitesimalen einen mathematischen Status zu verleihen. Seit dem 18. Jahrhundert wurden viele verschiedene Versuche unternommen (cf. Borovik & Katz, 2012). Glatte Infinitesimalanalysis, entwickelt aus der Idee von F. W. Lawvere in der Kategorientheorie ist eine andere modernere Konstruktion: in ihr sind alle Infinitesimale als eine Zahl ungleich ![]() definiert, deren Quadrat allerdings
definiert, deren Quadrat allerdings ![]() ist (cf. Bell, 2008).
ist (cf. Bell, 2008).
Literatur:
Bell, J.L. (2008). A primer of infinitesimal analysis, 2nd edition. Cambridge : Cambridge University Press.
Borovik, B. & Katz, M. (2012) Who Gave you the Cauchy-Weierstrass Tale? The Dual History of Rigorous Calculus. Foundations of Science 17, no. 3, 245-276.
Berkeley, G. (1734). The Analyst. http://www.maths.tcd.ie/pub/HistMath/People/Berkeley/Analyst/
Benoît, E., Callot, J.L., Diener, F., & Diener. M. (1981). Chasse au canard. Collectanea Mathematica, 32.1, 38-74.
http://collectanea.ub.edu/index.php/Collectanea/article/view/3537/4216
Deledicq A., & Diener, M. (1989). Leçons de calcul infinitésimal. Collection U. Paris : Armand Colin.
Diener, M., & Diener, F. (Eds.). (1995). Non standard analysis in practice. Berlin : Springer Verlag.
Henle, J.M., & Kleinberg, E.M. (1979). Infinitesimal Calculus. Cambridge : MIT Press.
Hodgson, B. (1994). Le calcul infinitésimal. In, D.F. Robitaille, D.H. Wheeler et C. Kieran (Eds.), Choix de conférence du 7e Congrès international sur l’enseignement des mathématiques (ICME-7), pp. 157-170. Québec : Presses de l’Université Laval.
Document.
Keisler, H.J. (1976). Elementary calculus : An infinitesimal approach. Boston : Prindle, Weber & Schmidt.
Lakatos, I. (1978): Cauchy and the continuum: the significance of nonstandard analysis for the history and philosophy of mathematics. Math. Intelligencer 1, no. 3, 151–161 (paper originally presented in 1966).
Lutz, R. & Goze, M. (1982). Non standard analysis : a practical guide with applications. Springer Lecture Notes in Mathematics, vol. 881. Berlin : Springer.
Marquis de l’Hôpital, G.F.A. (1696). Analyse des infiniment petits pour l’intelligence des lignes courbes. Paris : Imprimerie Royale.
Nelson, E. (1977). Internal set Theory, a new approach to NSA, Bull. Amer. Math. Soc., vol. 83, no 6, 1165-1198.
Robinson, A. (1996). Non standard analysis. North Holland, Amsterdam.
Skolem, Th. (1934). Über die Nicht-charakterisierbarkeit der Zahlenreihe mittels endlich oder abzählbar unendlich vieler Aussagen mit ausschliesslich Zahlenvariablen. Fundam. Math. 23, 150-161
![]()
![]() Der Umfang dieses Calculus ist groß: Es ist geeignet sowohl für mechanische als auch geometrische Kurven; Wurzelzeichen sind ihm gleichgütig und oft nützlich; es kann auf beliebig viele Unbestimmte angewendet werden; der Vergleich von infinitesimal kleinen Mengen jeglicher Art ist genauso einfach. Dadurch entsteht eine Unendlichkeit an überraschenden Entdeckungen in Bezug auf gekrümmte als auch auf gerade Tangenten, Fragen bezüglich Maxima und Minima, Wendepunkte und Scheitelpunkte von Kurven, entwickelt und beißend durch Reflektion oder Refraktion, etc., wie in diesem Buch erklärt. (unsere Übersetzung)
Der Umfang dieses Calculus ist groß: Es ist geeignet sowohl für mechanische als auch geometrische Kurven; Wurzelzeichen sind ihm gleichgütig und oft nützlich; es kann auf beliebig viele Unbestimmte angewendet werden; der Vergleich von infinitesimal kleinen Mengen jeglicher Art ist genauso einfach. Dadurch entsteht eine Unendlichkeit an überraschenden Entdeckungen in Bezug auf gekrümmte als auch auf gerade Tangenten, Fragen bezüglich Maxima und Minima, Wendepunkte und Scheitelpunkte von Kurven, entwickelt und beißend durch Reflektion oder Refraktion, etc., wie in diesem Buch erklärt. (unsere Übersetzung)
![]() ZFC steht für die Zermelo-Fraenkel-Axiome plus das Auswahlaxiom (siehe http://en.wikipedia.org/wiki/Zermelo–Fraenkel_set_theory).
ZFC steht für die Zermelo-Fraenkel-Axiome plus das Auswahlaxiom (siehe http://en.wikipedia.org/wiki/Zermelo–Fraenkel_set_theory).
![]() Das Axiom der Idealisierung sagt aus, dass für jede binäre Relation
Das Axiom der Idealisierung sagt aus, dass für jede binäre Relation ![]() , die klassisch ist (d.h. formuliert ohne die Benutzung des Prädikats
, die klassisch ist (d.h. formuliert ohne die Benutzung des Prädikats ![]() ), sind die folgenden zwei Aussagen äquivalent: (i) für jede endliche Standardmenge
), sind die folgenden zwei Aussagen äquivalent: (i) für jede endliche Standardmenge ![]() existiert ein
existiert ein ![]() so, dass für jedes
so, dass für jedes ![]() aus
aus ![]() ,
, ![]() ; (ii) Es gibt ein
; (ii) Es gibt ein ![]() so, dass für jedes
so, dass für jedes ![]() , das standard ist,
, das standard ist, ![]() .
.
The axiom of standardization says that for any property ![]() and any standard set
and any standard set ![]() , there is a standard part
, there is a standard part ![]() of
of ![]() whose standard elements are exactly the elements of
whose standard elements are exactly the elements of ![]() that satisfy
that satisfy ![]() . This axiom works whether
. This axiom works whether ![]() is a classical property or not.
is a classical property or not.
The axiom of transfer says that for any classical property ![]() ,
, ![]() is true for all
is true for all ![]() if and only if
if and only if ![]() is true for all
is true for all ![]() standard.
standard.
![]() Wenden Sie das Transferaxiom mit der Eigenschaft
Wenden Sie das Transferaxiom mit der Eigenschaft ![]() :
: ![]() an.
an.
![]() Im ersten Fall wird das Axiom der Idealisierung auf die binäre Relation
Im ersten Fall wird das Axiom der Idealisierung auf die binäre Relation ![]() in
in ![]() angewandt; im zweiten Fall wird es auf die binäre Relation
angewandt; im zweiten Fall wird es auf die binäre Relation ![]() in der betrachteten unendlichen Menge angewandt.
in der betrachteten unendlichen Menge angewandt.
![]() In dieser Tabelle werde alle Objekte
In dieser Tabelle werde alle Objekte ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() als Standard betrachtet.
als Standard betrachtet.
![]() In dieser Aussage werden
In dieser Aussage werden ![]() ,
, ![]() ,
, ![]() ,
, ![]() ebenfalls als Standard betrachtet.
ebenfalls als Standard betrachtet.
Andere Sprachen: Englisch, Französisch, Spanisch, Arabisch, Portugiesisch, Brasilien

 Deutsch
Deutsch 简体中文
简体中文  English
English  Français
Français  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português