 Vignette écrite par Michèle Artigue, Ferdinando Arzarello et Susanna Epp.
Vignette écrite par Michèle Artigue, Ferdinando Arzarello et Susanna Epp.
Etudier l’évolution de phénomènes conduit souvent à étudier des suites numériques, à s’interroger sur leurs types de croissance, et sur leur convergence éventuelle. Les exemples de croissance rencontrés dans l’enseignement secondaire sont en général des croissances polynomiales, exponentielles ou logarithmiques. Mais des suites, même définies de façon très simple, peuvent avoir des comportements complexes comme le montrent les suites chaotiques de la théorie des systèmes dynamiques (Perrin, 2008). Et des suites définies de façon très simples, dont on a calculé des millions de termes, peuvent être source de questions qui défient les mathématiciens depuis plusieurs décennies. Ainsi en est-il par exemple de la question de savoir si les suites connues comme suites « ![]() » ou suites de Syracuse introduites par Luther Collatz en 1937, finissent ou non toujours par atteindre la valeur
» ou suites de Syracuse introduites par Luther Collatz en 1937, finissent ou non toujours par atteindre la valeur ![]() (http://arxiv.org/abs/math/0608208v5).
(http://arxiv.org/abs/math/0608208v5).
Les suites que nous considérons dans cette vignette, introduites par le logicien britannique Reuben L. Goodstein en 1944, ont un comportement très différent. Leur croissance initiale, extraordinairement rapide, laisse penser qu’elles vont tendre vers l’infini, mais étonnamment elles finissent toujours par devenir décroissantes et tendre vers ![]() . La preuve de ce résultat nécessite une généralisation du raisonnement par récurrence à des ordinaux infinis mais sa mécanique en est tout à fait compréhensible. Pour l’expliquer, nous allons introduire, comme le fait Hodgson (2004), un objet plus facile à appréhender : les suites faibles de Goodstein.
. La preuve de ce résultat nécessite une généralisation du raisonnement par récurrence à des ordinaux infinis mais sa mécanique en est tout à fait compréhensible. Pour l’expliquer, nous allons introduire, comme le fait Hodgson (2004), un objet plus facile à appréhender : les suites faibles de Goodstein.
1. Les suites faibles de Goodstein
Comme Hodgson, prenons comme point de départ, le nombre ![]() . Comme tout entier positif, il admet une décomposition additive unique sur la base des puissances de
. Comme tout entier positif, il admet une décomposition additive unique sur la base des puissances de ![]() (voir [1]):
(voir [1]): ![]() . La suite faible de Goodstein dont le premier terme
. La suite faible de Goodstein dont le premier terme ![]() est
est ![]() est alors définie de la façon suivante. Pour obtenir le terme
est alors définie de la façon suivante. Pour obtenir le terme ![]() , on remplace dans l’écriture précédente la base
, on remplace dans l’écriture précédente la base ![]() par la base
par la base ![]() , et on soustrait
, et on soustrait ![]() au nombre obtenu. On obtient ainsi
au nombre obtenu. On obtient ainsi ![]() . En base 3, ce nombre a en fait comme décomposition additive :
. En base 3, ce nombre a en fait comme décomposition additive : ![]() . C’est de cette décomposition que l’on repart pour déterminer
. C’est de cette décomposition que l’on repart pour déterminer ![]() en remplaçant la base
en remplaçant la base ![]() par la base
par la base ![]() et en soustrayant
et en soustrayant ![]() au nombre obtenu comme précédemment, et ainsi de suite tant que le terme de la suite est non nul. On obtient ainsi successivement :
au nombre obtenu comme précédemment, et ainsi de suite tant que le terme de la suite est non nul. On obtient ainsi successivement :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Table 1: Termes initiaux d’une suite de Goodstein faible.
Les termes de la suite semblent donc croître très vite. Est-ce toujours le cas ? Non, si l’on choisit par exemple : ![]() , alors
, alors ![]() . Pour
. Pour ![]() , on a
, on a ![]() ,
, ![]() et
et ![]() . On vérifiera de même que la suite de premier terme
. On vérifiera de même que la suite de premier terme ![]() ne dépasse jamais
ne dépasse jamais ![]() et atteint
et atteint ![]() en cinq coups (voir [2]). Mais dès que la décomposition du nombre de départ fait intervenir des puissances élevées de
en cinq coups (voir [2]). Mais dès que la décomposition du nombre de départ fait intervenir des puissances élevées de ![]() , la croissance initiale est très rapide comme celle observée pour
, la croissance initiale est très rapide comme celle observée pour ![]() et conduit à penser que la suite tend vers l’infini. Comment le fait de retrancher
et conduit à penser que la suite tend vers l’infini. Comment le fait de retrancher ![]() pourrait-il compenser l’impressionnante croissance qui est générée par l’accroissement d’une unité de la base ?
pourrait-il compenser l’impressionnante croissance qui est générée par l’accroissement d’une unité de la base ?
Et pourtant…. Regardons plus soigneusement les expressions écrites ci-dessus. Si les termes successifs de la suite de premier terme ![]() croissent rapidement, les exposants intervenant dans les représentations dans les bases successives considérées tendent, eux, cependant à décroître. L’exposant
croissent rapidement, les exposants intervenant dans les représentations dans les bases successives considérées tendent, eux, cependant à décroître. L’exposant ![]() a été remplacé par un exposant
a été remplacé par un exposant ![]() dans
dans ![]() . Il finira par être remplacé par un exposant
. Il finira par être remplacé par un exposant ![]() et nécessairement l’exposant
et nécessairement l’exposant ![]() , à son tour, finira à son tour par être remplacé par un exposant
, à son tour, finira à son tour par être remplacé par un exposant ![]() …
…
C’est cette caractéristique, commune à toutes les suites de Goodstein, qui va permettre de montrer qu’elles convergent vers ![]() . Pour cela, il faut faire intervenir, comme annoncé, des ordinaux infinis. Nous faisons donc une digression de ce côté-là.
. Pour cela, il faut faire intervenir, comme annoncé, des ordinaux infinis. Nous faisons donc une digression de ce côté-là.
2. Ordinaux et bon ordre
Ordinaux:
Les ordinaux sont associés à l’idée de rangement. On peut ranger les éléments d’un ensemble fini en les numérotant à l’aide des entiers : premier, deuxième…. La notion d’ordinal transfini, due au mathématicien Georg Cantor qui l’a développée dans une série d’articles parus à la fin du 19ème siècle, prolonge cette idée. Le premier ordinal plus grand que tous les entiers est noté ![]() , c’est le premier ordinal infini. Il a un successeur
, c’est le premier ordinal infini. Il a un successeur ![]() , qui a lui-même pour successeur
, qui a lui-même pour successeur ![]() , qui a lui-même pour successeur… Le plus petit ordinal plus grand que tous les
, qui a lui-même pour successeur… Le plus petit ordinal plus grand que tous les ![]() , est
, est ![]() noté
noté ![]() (voir [3]). Le plus petit ordinal plus grand que tous les
(voir [3]). Le plus petit ordinal plus grand que tous les ![]() est
est ![]() et, de même, le plus petit ordinal plus grand que tous les
et, de même, le plus petit ordinal plus grand que tous les ![]() est noté
est noté ![]() .
.
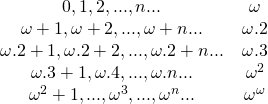
On note ![]() le premier ordinal limite supérieur à tous les ordinaux qui sont des puissances itérées de
le premier ordinal limite supérieur à tous les ordinaux qui sont des puissances itérées de ![]() Nous nous arrêterons là mais bien sûr
Nous nous arrêterons là mais bien sûr ![]() a lui aussi un successeur
a lui aussi un successeur ![]() et la chaîne continue. En fait tous les ordinaux dont il a été question jusqu’ici ne constituent que le début de cette chaîne des ordinaux puisqu’ils sont tous dénombrables : ils peuvent en effet être tous mis en bijection avec l’ensemble des entiers.
et la chaîne continue. En fait tous les ordinaux dont il a été question jusqu’ici ne constituent que le début de cette chaîne des ordinaux puisqu’ils sont tous dénombrables : ils peuvent en effet être tous mis en bijection avec l’ensemble des entiers.
Ordinaux et bon ordre:
L’ordre sur les ordinaux, comme celui sur les entiers, est un bon ordre : tout ensemble non vide d’ordinaux a un plus petit élément. De cette propriété, qui pour les entiers est à la base du raisonnement par récurrence, on déduit qu’il ne peut exister de suite infinie strictement décroissante d’ordinaux. En effet supposons qu’une telle suite existe. Notons ![]() l’ensemble de ses termes :
l’ensemble de ses termes : ![]() .
. ![]() a un plus petit élément, notons le
a un plus petit élément, notons le ![]() . C’est un terme de la suite donc il existe un
. C’est un terme de la suite donc il existe un ![]() tel que
tel que ![]() . Mais alors
. Mais alors ![]() et appartient à
et appartient à ![]() , ce qui contredit la définition de
, ce qui contredit la définition de ![]() . Une telle suite n’existe donc pas. La propriété de bon ordre permet donc de généraliser aux ordinaux les raisonnements dits « par descente infinie » que l’on peut faire sur les entiers.
. Une telle suite n’existe donc pas. La propriété de bon ordre permet donc de généraliser aux ordinaux les raisonnements dits « par descente infinie » que l’on peut faire sur les entiers.
Après cette parenthèse, revenons aux suites de Goodstein.
3. La preuve de la convergence vers ![]() des suites faibles de Goodstein
des suites faibles de Goodstein
A chaque suite faible de Goodstein, on va associer une suite strictement décroissante d’ordinaux. Pour cela, on procède de la façon suivante. A l’étape ![]() ,
, ![]() est décomposé sur la base des puissances de
est décomposé sur la base des puissances de ![]() . Dans cette décomposition, remplaçons systématiquement la base par
. Dans cette décomposition, remplaçons systématiquement la base par ![]() . Pour la suite associée à
. Pour la suite associée à ![]() , on obtient ainsi une nouvelle suite
, on obtient ainsi une nouvelle suite ![]() dont les premiers termes sont les suivants :
dont les premiers termes sont les suivants :
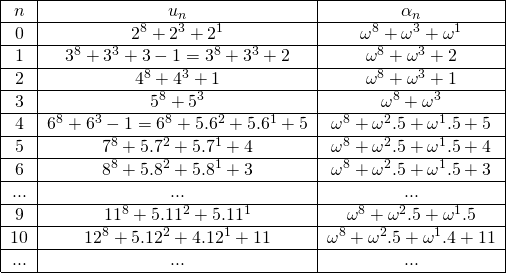
Table 2: La suite des ordinaux correspondant à une suite faible de Goodstein.
Vu son mode de construction La suite ![]() majore la suite
majore la suite ![]() , et elle est de plus décroissante stricte. En effet, le passage d’un terme au suivant se fait forcément de l’une des deux façons suivantes :
, et elle est de plus décroissante stricte. En effet, le passage d’un terme au suivant se fait forcément de l’une des deux façons suivantes :
- Soit le reste dans la division par la base est non nul et on le diminue de
 , tout en effectuant le changement de base (c’est le cas pour le passage de
, tout en effectuant le changement de base (c’est le cas pour le passage de 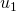 à
à 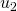 , de
, de 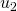 à
à 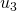 et de
et de 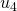 à
à 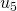 ).
). - Soit ce reste est nul et pour obtenir la décomposition additive du terme suivant, après avoir fait le changement de base, il faut casser le terme de la décomposition ayant le plus faible exposant (c’est le cas pour le passage de
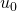 à
à 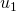 , de
, de 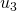 à
à 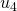 et de
et de  à
à  ). Mais dans les deux cas, le nouvel ordinal obtenu est strictement inférieur au précédent.
). Mais dans les deux cas, le nouvel ordinal obtenu est strictement inférieur au précédent.
Nous invitions le lecteur à écrire les deux suites ![]() et
et ![]() lorsque
lorsque ![]() . Pour quelle valeur de
. Pour quelle valeur de ![]() a-t-on
a-t-on ![]() ? Que vaut alors
? Que vaut alors ![]() et que se passe-t-il pour les termes suivants des deux suites ? (voir 4).
et que se passe-t-il pour les termes suivants des deux suites ? (voir 4).
Or, comme les ordinaux sont bien ordonnés, il n’existe pas de suite infinie décroissante stricte d’ordinaux. Il existe donc un ![]() tel que
tel que ![]() . Et, vu que pour tout
. Et, vu que pour tout ![]() ,
, ![]() , on en déduit que
, on en déduit que ![]() est aussi égal à
est aussi égal à ![]() . La suite
. La suite ![]() atteint donc elle aussi
atteint donc elle aussi ![]() en un nombre fini de pas qui peut être bien sûr très grand.
en un nombre fini de pas qui peut être bien sûr très grand.
Nous sommes prêts maintenant à aborder les suites de Goodstein proprement dites. Elles sont définies de façon légèrement différente et leur croissance est beaucoup plus spectaculaire ! Mais, curieusement, le principe de la preuve est similaire.
4. Les suites de Goodstein
Revenons au nombre ![]() et à sa décomposition sur la base des puissances de
et à sa décomposition sur la base des puissances de ![]() :
: ![]() . Dans cette décomposition, les exposants n’ont pas été exprimés en base
. Dans cette décomposition, les exposants n’ont pas été exprimés en base ![]() . C’est ce que nous allons faire maintenant :
. C’est ce que nous allons faire maintenant : ![]() et
et ![]() . D’où une nouvelle représentation de
. D’où une nouvelle représentation de ![]() qui, cette fois, ne fait intervenir que des chiffres inférieurs ou égaux à la base. Pour construire le terme suivant de la suite de Goodstein, on remplace toutes les occurrences de la base
qui, cette fois, ne fait intervenir que des chiffres inférieurs ou égaux à la base. Pour construire le terme suivant de la suite de Goodstein, on remplace toutes les occurrences de la base ![]() par des
par des ![]() et on enlève
et on enlève ![]() comme on le faisait pour la suite faible. Puis on itère le processus.
comme on le faisait pour la suite faible. Puis on itère le processus.
Partant de ![]() , on obtient ainsi successivement (voir [5]):
, on obtient ainsi successivement (voir [5]):
![]()
![]()
![]()
![]()
![]()
![]()
Table 3.
Comme on le voit, la croissance est cette fois impressionnante et, même avec un ordinateur, vous ne pourrez pas pousser très loin l’exploration ! Et pourtant, cette suite, comme toutes les suites de Goodstein, finit par devenir décroissante et converge vers 0. La preuve est en tout point similaire à celle que nous avons esquissée pour les suites faibles. On associe une suite ![]() à la suite
à la suite ![]() en remplaçant chaque occurrence de la base par
en remplaçant chaque occurrence de la base par ![]() . Et l’on montre par un raisonnement analogue à celui fait plus haut que la suite d’ordinaux ainsi obtenus est strictement décroissante. Ce raisonnement se généralise à toutes les suites de Goodstein, les ordinaux qui interviennent étant tous dénombrables et inférieurs à
. Et l’on montre par un raisonnement analogue à celui fait plus haut que la suite d’ordinaux ainsi obtenus est strictement décroissante. Ce raisonnement se généralise à toutes les suites de Goodstein, les ordinaux qui interviennent étant tous dénombrables et inférieurs à ![]() (ils étaient tous inférieurs à
(ils étaient tous inférieurs à ![]() pour les suites faibles de Goodstein).
pour les suites faibles de Goodstein).
Cette démonstration est sans aucun doute élégante mais, pour démontrer un théorème portant sur des suites d’entiers, elle nous a obligés à sortir du cadre de l’arithmétique usuelle, appelée aussi arithmétique de Peano car, le premier, il en a formalisé les axiomes. Il nous a fallu nous situer dans le cadre plus général de la théorie des ensembles pour faire intervenir des ordinaux transfinis. Et pourtant le langage de l’arithmétique de Peano suffit à formuler le théorème de Goodstein qui affirme que toutes les suites de Goodstein convergent vers ![]() ! Il est alors normal de se demander s’il est possible de trouver une autre démonstration qui, elle, ne ferait pas sortir du cadre de l’arithmétique usuelle. La réponse est connue, c’est : Non ! Elle a été apportée par Laurie Kirby et Jeff Paris en 1982, soit près de 40 ans après l’introduction des suites de Goodstein. Ils ont en effet montré que le théorème de Goodstein pouvait se ramener à celui de Gentzen (1936) qui prouve la consistance de l’arithmétique de Peano. Or l’on sait, par le théorème d’incomplétude de Gödel, que cette consistance n’est pas démontrable dans l’axiomatique de Peano elle-même. Donc le théorème de Goodstein n’est pas non plus démontrable dans l’arithmétique de Peano. Inutile donc pour les mathématiciens de dépenser leur énergie à chercher une telle preuve !
! Il est alors normal de se demander s’il est possible de trouver une autre démonstration qui, elle, ne ferait pas sortir du cadre de l’arithmétique usuelle. La réponse est connue, c’est : Non ! Elle a été apportée par Laurie Kirby et Jeff Paris en 1982, soit près de 40 ans après l’introduction des suites de Goodstein. Ils ont en effet montré que le théorème de Goodstein pouvait se ramener à celui de Gentzen (1936) qui prouve la consistance de l’arithmétique de Peano. Or l’on sait, par le théorème d’incomplétude de Gödel, que cette consistance n’est pas démontrable dans l’axiomatique de Peano elle-même. Donc le théorème de Goodstein n’est pas non plus démontrable dans l’arithmétique de Peano. Inutile donc pour les mathématiciens de dépenser leur énergie à chercher une telle preuve !
En revanche, et cela peut paraître étonnant, la convergence vers ![]() des suites faibles de Goodstein peut, elle, être démontrée sans sortir du cadre de cette arithmétique car on peut y exprimer des inductions qui ne dépassent pas l’ordinal
des suites faibles de Goodstein peut, elle, être démontrée sans sortir du cadre de cette arithmétique car on peut y exprimer des inductions qui ne dépassent pas l’ordinal ![]() . Une telle démonstration nous a été proposée par E.A. Cichon qui avait introduit les suites faibles de Goodstein dans (Cichon, 1983). Précisons, pour le lecteur intéressé, que l’on introduit pour cela les
. Une telle démonstration nous a été proposée par E.A. Cichon qui avait introduit les suites faibles de Goodstein dans (Cichon, 1983). Précisons, pour le lecteur intéressé, que l’on introduit pour cela les ![]() -uplets de coefficients de la décomposition des
-uplets de coefficients de la décomposition des ![]() en base
en base ![]() et que l’on met sur ces m-uplets l’ordre lexicographique qui est un bon ordre.
et que l’on met sur ces m-uplets l’ordre lexicographique qui est un bon ordre.
5. Suites de Goodstein et jeu de l’hydre
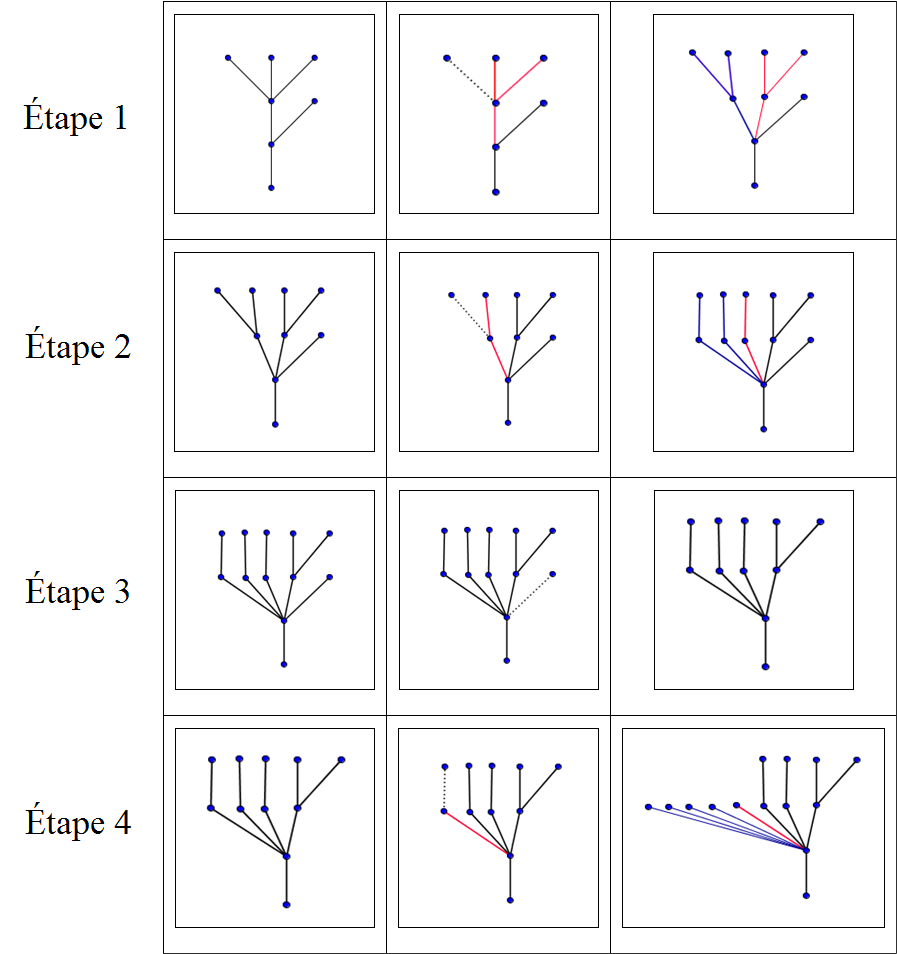
Dans leur article, Kirby et Paris, mentionnent un autre processus qui présente des similarités profondes avec les suites de Goodstein : le jeu de l’hydre (voir aussi (Dehornoy, 2001)). Il tient son nom de la référence mythologique au combat d’Hercule contre l’hydre de Lerne dont les têtes coupées repoussaient sans cesse. C’est un jeu dans lequel l’hydre est modélisée par un arbre. Les têtes de l’hydre sont, à tout instant, les sommets terminaux de l’arbre. Si Hercule coupe une tête qui n’est pas directement reliée à la racine de l’arbre en supprimant l’arête associée, l’hydre se régénère à partir des sommets situés à deux niveaux sous la tête coupée. Elle peut le faire de différentes façons. Par exemple, dans l’exemple ci-dessous utilisé par Kirby et Paris et repris par Hodgson, si la tête est coupée à l’étape ![]() du jeu, l’hydre génère
du jeu, l’hydre génère ![]() copies de la partie de l’arbre située au-dessus de ce nœud. A chaque étape, la partie coupée est indiquée en pointillés, la partie qui se régénère en rouge et la partie qui a repoussé en bleu.
copies de la partie de l’arbre située au-dessus de ce nœud. A chaque étape, la partie coupée est indiquée en pointillés, la partie qui se régénère en rouge et la partie qui a repoussé en bleu.
On peut montrer que, quelle que soit la configuration de l’hydre, la stratégie d’Hercule et celle de l’hydre, Hercule finit toujours par couper toutes les têtes, même si cela peut nécessiter un temps très très long. La démonstration, comme dans le cas de la convergence des suites de Goodstein, est basée sur l’association aux arbres successifs d’une suite strictement décroissante d’ordinaux. Comme on peut le conjecturer à partir des représentations ci-dessus, l’arbre peut s’étendre en largeur mais sa hauteur, elle, finit nécessairement par diminuer. On pourra trouver une simulation du jeu de l’hydre sur le site : http://math.andrej.com/wp-content/uploads/2008/02/Hydra/hydraApplet.html
6. Quelques leçons à tirer de cet exemple
Cet exemple nous semble intéressant à plus d’un titre. Il montre tout d’abord que la logique n’est pas qu’affaire métamathématique. Des théorèmes comme le théorème d’incomplétude de Gödel qui peuvent paraître justement de nature exclusivement métamathématique, des objets qui peuvent paraître très éloignés des mathématiques élémentaires comme les ordinaux transfinis, s’incarnent dans des théorèmes qui portent sur des propriétés d’objets mathématiques ordinaires (suites, arbres). Il attire aussi notre attention sur le fait que démontrer un résultat fait uniquement sens dans le cadre d’un langage et d’une théorie qui s’exprime dans ce langage, même si ceci reste souvent pour nous implicite. Une propriété concernant des entiers peut ainsi pouvoir être démontrée dans la théorie des ensembles et non dans la théorie de Peano qui est donc strictement plus faible.
Mais cet exemple nous semble aussi instructif au-delà de la seule logique. Il nous montre d’abord les limites de l’intuition : des suites dont tout nous porte a priori à croire qu’elles vont tendre vers l’infini vont finalement devenir décroissantes et atteindre ![]() en un nombre fini de pas. Il nous montre l’intérêt qu’il peut y avoir pour comprendre un phénomène à modifier le problème initial en un problème plus accessible : ici c’est celui des suites faibles de Goodstein pour lequel l’exploration est davantage possible. Il nous montre comment l’étude d’exemples génériques, dans ce cas simplifié, permet de comprendre la raison d’être du phénomène avant même que l’on introduise, pour formaliser le raisonnement dans le cas général, des ordinaux transfinis. Il nous donne enfin à voir à la fois la puissance et les limites de la technologie, sa capacité à nous faire ressentir la croissance rapide de la suite, mais aussi ses limites aussi face à l’explosion numérique que génère ce processus.
en un nombre fini de pas. Il nous montre l’intérêt qu’il peut y avoir pour comprendre un phénomène à modifier le problème initial en un problème plus accessible : ici c’est celui des suites faibles de Goodstein pour lequel l’exploration est davantage possible. Il nous montre comment l’étude d’exemples génériques, dans ce cas simplifié, permet de comprendre la raison d’être du phénomène avant même que l’on introduise, pour formaliser le raisonnement dans le cas général, des ordinaux transfinis. Il nous donne enfin à voir à la fois la puissance et les limites de la technologie, sa capacité à nous faire ressentir la croissance rapide de la suite, mais aussi ses limites aussi face à l’explosion numérique que génère ce processus.
Références :
[1] Un entier ![]() appelé la base étant choisi, tout entier naturel
appelé la base étant choisi, tout entier naturel ![]() peut s’écrire de façon unique sous la forme suivante, dénommée sa décomposition en base
peut s’écrire de façon unique sous la forme suivante, dénommée sa décomposition en base ![]() :
: ![]() , tous les
, tous les ![]() étant des entiers compris entre
étant des entiers compris entre ![]() et
et ![]() , et
, et ![]() étant non nul (
étant non nul (![]() est alors supérieur ou égal à
est alors supérieur ou égal à ![]() et inférieur strict à
et inférieur strict à ![]() ). L’écriture usuelle des nombres correspond à leur décomposition dans la base dix.
). L’écriture usuelle des nombres correspond à leur décomposition dans la base dix.
[2] La suite de valeur initiale ![]() a pour termes successifs :
a pour termes successifs : ![]() ,
, ![]() qui est plus petit que la base, et donc
qui est plus petit que la base, et donc ![]() ,
, ![]() et
et ![]() .
.
[3] On prolonge en effet aux ordinaux les opérations sur les entiers mais, attention, la commutativité de l’addition et de la multiplication ne sont pas conservées.
[4] Les réponses sont les suivantes : ![]() pour
pour ![]() , et alors
, et alors ![]() . Pour obtenir
. Pour obtenir ![]() , on remplace la base
, on remplace la base ![]() par la base
par la base ![]() et on soustrait
et on soustrait ![]() , donc
, donc ![]() qui est plus petit que la base.On a alors
qui est plus petit que la base.On a alors ![]() . A partir de l’indice
. A partir de l’indice ![]() , les suites
, les suites ![]() et
et ![]() sont égales et forment une suite arithmétique décroissante de raison
sont égales et forment une suite arithmétique décroissante de raison ![]() . Il s’ensuit que
. Il s’ensuit que ![]() .
.
[5] On pourra pour cela utiliser le site http://www.wolframalpha.com.
[6] Cichon, E. A. (1983). A Short Proof of Two Recently Discovered Independence Results Using Recursion Theoretic Methods, Proc. Amer. Math. Soc., 87, 704-706.
[7] Dehornoy, P. (2001). L’infini est-il nécessaire ? Pour la Science, Dossier.
[8] Dehornoy, P. (2009). Cantor et les infinis.
[9] Hodgson B. (2007). Envolées intersidérales… à destination terrestre !. Accromath. Hiver-printemps 2007, www.accromath.ca
[10] Hodgson B. (2004). Herculean of Sisyphean tasks? EMS Newsletter, March 2004, pp. 11-16.
[11] Goodstein, R. L. (1944). On the Restricted Ordinal Theorem, Journal of Symbolic Logic, 9, 33-41,
[12] Kirby, L. and Paris, J. (1982). Accessible Independence Results for Peano Arithmetic, Bulletin of the London Mathematical Society, 14, 285-293.
[13] Perrin, D. (2008). La suite logistique et le chaos.
Ce post est disponible en: Anglais, Allemand, Italien, Espagnol, Arabe, Khmère, Portugais - du Brésil

 Français
Français 简体中文
简体中文  English
English  Deutsch
Deutsch  Italiano
Italiano  Español
Español  العربية
العربية  Khmer
Khmer  Português
Português
Très bonne vignette, bravo ! Très clair et interessant.
Il me reste cependant une question, après lecture de l’article: en quoi sort-on de l’arithmétique de Peano en faisant intervenir des ordinaux supérieurs à omega^omega, et pourquoi n’en sort-on pas quand on reste en dessous de omega^omega ?
Merci,
Nicolas
L’arithmetique de Peano ne concerne que les nombre entiers, c’est a dire l’arithmetique classique. Les ordinaux infinis comme omega n’en font pas partie.
Parce que quand on reste “sous” ω^ω, en fait, les ordinaux ne sont pas nécessaires pour établir une preuve, ils sont juste une façon élégante d’emboîter un nombre fini mais quelconque de récurrences