 Versión original escrita por Christiane Rousseau.
Versión original escrita por Christiane Rousseau.
Desde sus comienzos, Google se convirtió en «el» motor de búsqueda. Esto es debido a la supremacía de su algoritmo de jerarquización: el algoritmo PageRank. De hecho, debido a la enorme cantidad de páginas web en la World Wide Web, muchas búsquedas finalizan con miles o millones de resultados. Si estas páginas no estuvieran adecuadamente ordenadas, la búsqueda no sería de ninguna utilidad, ya que nadie es capaz de explorar millones de entradas.
¿Cómo funciona al algoritmo PageRank?
Esto se explicará más adelante, pero antes vamos a hacer una búsqueda en Google. En junio de 2010 se obtuvieron 16.300.000 resultados para Klein project, si bien el proyecto estaba comenzando. En esta fecha en concreto, la primera entrada era
http://www.mathunion.org/icmi/other-activities/klein-project/introduction/
en lugar de
http://www.kleinproject.org/
La primera url es la dirección web de una página que está localizada en el sitio web de la Unión Matemática Internacional (International Mathematical Union): http://www.mathunion.org. Como este es un organismo importante, su página web oficial aparece la primera cuando se realiza la búsqueda «International Mathematical Union». Es más, transmite parte de su importancia a todas sus páginas, una de las cuales es
Cabría esperar que dentro de unos pocos meses la página
apareciera la primera en la búsqueda de Klein project.
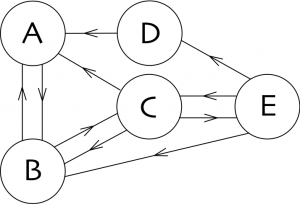
Para explicar el algoritmo se modela la red mediante un grafo orientado. Los vértices son las páginas y las aristas orientadas son los enlaces entre páginas. Como ya hemos explicado, cada página corresponde a una url diferente. Por tanto, un sitio web puede contener muchas páginas pero este modelo no diferencia entre las páginas individuales de un sitio web y su página principal. Sin embargo, es más probable que el algoritmo dé más valor a la página principal de un sitio web importante.
Un ejemplo sencillo

Consideremos el ejemplo de la sencilla red de la izquierda, compuesta por cinco páginas llamadas ![]() ,
, ![]() ,
, ![]() ,
, ![]() y
y ![]() . Esta red tiene pocos enlaces: en
. Esta red tiene pocos enlaces: en ![]() hay solamente un enlace a
hay solamente un enlace a ![]() , mientras que si estamos en
, mientras que si estamos en ![]() encontramos tres enlaces y podemos elegir entre pasar a
encontramos tres enlaces y podemos elegir entre pasar a ![]() ,
, ![]() o
o ![]() . Notar que hay al menos un enlace desde cada página.
. Notar que hay al menos un enlace desde cada página.
Proponemos un sencillo juego, que consiste en dar un paseo aleatorio por el grafo orientado. Comenzando en una página cualquiera, en cada paso elegimos un enlace al azar en la página en la que nos encontramos y lo seguimos. Por ejemplo, en nuestra red, si comenzamos en ![]() , entonces podemos elegir entre ir a
, entonces podemos elegir entre ir a ![]() o a
o a ![]() con probabilidad
con probabilidad ![]() para cada caso, mientras que si empezamos en
para cada caso, mientras que si empezamos en ![]() , entonces necesariamente tenemos que ir a
, entonces necesariamente tenemos que ir a ![]() con probabilidad
con probabilidad ![]() . Si repetimos el juego,
. Si repetimos el juego,
Para automatizar el proceso, resumimos la información de la red en la siguiente matriz ![]() , donde cada columna representa la página de salida y cada fila es la página de destino.
, donde cada columna representa la página de salida y cada fila es la página de destino.
![Rendered by QuickLaTeX.com \[P=\begin{matrix} \begin{matrix} A & B & C & D & E \end{matrix} & \\ \left(\ \ \begin{matrix} 0 & \frac12 & \frac13 & 1 & 0 \\ 1 & 0 & \frac13 & 0 & \frac13 \\ 0 & \frac12 & 0 & 0 & \frac13 \\ 0 & 0 & 0 & 0 & \frac13 \\ 0 & 0 & \frac13 & 0 & 0 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix} \end{matrix}\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-4812e42c3ece7134f590140ea350177a_l3.png)
Notar que la suma de todas los valores de una misma columna de ![]() es igual a
es igual a ![]() y que todas las entradas de la matriz son mayores o iguales que cero. Una matriz que satisface estas dos propiedades es de un tipo muy especial: es la matriz de un proceso de cadena de Markov, también conocida como matriz de transición del proceso de Markov. Este tipo de matrices tienen siempre como valor propio
y que todas las entradas de la matriz son mayores o iguales que cero. Una matriz que satisface estas dos propiedades es de un tipo muy especial: es la matriz de un proceso de cadena de Markov, también conocida como matriz de transición del proceso de Markov. Este tipo de matrices tienen siempre como valor propio ![]() y existe un vector propio de valor propio
y existe un vector propio de valor propio ![]() cuyas componentes son todas menores o iguales que
cuyas componentes son todas menores o iguales que ![]() y mayores o iguales que
y mayores o iguales que ![]() y cuya suma es
y cuya suma es ![]() . Antes de definir valores y vectores propios, vamos a explorar las ventajas de la representación matricial del grafo de la red.
. Antes de definir valores y vectores propios, vamos a explorar las ventajas de la representación matricial del grafo de la red.
Consideramos una variable aleatoria ![]() con valores en el conjunto de páginas
con valores en el conjunto de páginas ![]() ; este conjunto contiene
; este conjunto contiene ![]() páginas.
páginas. ![]() representa la página en la que nos encontramos después de
representa la página en la que nos encontramos después de ![]() pasos del camino aleatorio. Por tanto, si
pasos del camino aleatorio. Por tanto, si ![]() es el elemento de la matriz ubicado en la
es el elemento de la matriz ubicado en la ![]() -ésima fila y
-ésima fila y ![]() -ésima columna, entonces
-ésima columna, entonces ![]() representa la probabilidad condicionada de que nos encontremos en la
representa la probabilidad condicionada de que nos encontremos en la ![]() -ésima página en el paso
-ésima página en el paso ![]() , supuesto que estábamos en la
, supuesto que estábamos en la ![]() -ésima página en el paso
-ésima página en el paso ![]() :
:
![]()
¡Notar que esta probabilidad no depende de ![]() ! Por ello, se dice que un proceso de cadena de Markov no tiene memoria. No es difícil de probar que las probabilidades después de dos pasos pueden resumirse en la matriz
! Por ello, se dice que un proceso de cadena de Markov no tiene memoria. No es difícil de probar que las probabilidades después de dos pasos pueden resumirse en la matriz ![]() . Probémoslo (el lector puede omitir la demostración, si lo desea). Del teorema de la probabilidad total se deduce que
. Probémoslo (el lector puede omitir la demostración, si lo desea). Del teorema de la probabilidad total se deduce que
![Rendered by QuickLaTeX.com \[\text{Prob}(X_{n+2}=i \mid X_n=j)=\sum_{k=1}^N\text{Prob}(X_{n+2}= i \;\text{y}\; X_{n+1}=k \mid X_n=j).\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-1316aa393541c6613c1b033172042db2_l3.png)
Por la definición de probabilidad condicionada,
![Rendered by QuickLaTeX.com \[\text{Prob}(X_{n+2}=i \mid X_n=j)=\sum_{k=1}^N\frac{\text{Prob}(X_{n+2}= i \;\text{y}\; X_{n+1}=k \;\text{y}\; X_n=j)} {\text{Prob}(X_n=j)}.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-c8ef89a0a23da52adf9f0fd90270c992_l3.png)
Usamos ahora un truco muy conocido: multiplicar y dividir por la misma cantidad:
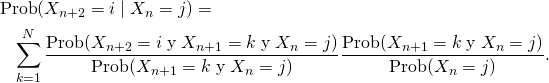
El primer cociente es igual a
![]()
ya que los procesos de cadena de Markov no tienen memoria del paso anterior. Por tanto,
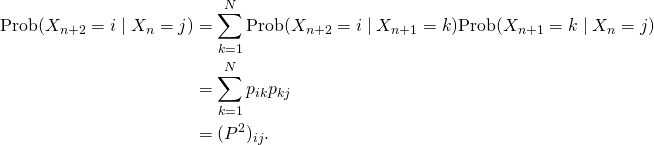
En nuestro ejemplo,
![Rendered by QuickLaTeX.com \[P^2=\begin{matrix} \begin{matrix} A & B & C & D & E \end{matrix} & \\ \left(\ \ \begin{matrix}\frac12 & \frac16 & \frac16 & 0 & \frac{11}{18} \\ 0 & \frac23 & \frac49 & 1 & \frac19 \\ \frac12 & 0 & \frac5{18} & 0 & \frac16 \\ 0 & 0 & \frac19 & 0 & 0 \\ 0 & \frac16 & 0 & 0 & \frac19 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix} \end{matrix}\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-79f1d41b7d9bb843aedc73e433c5e74a_l3.png)
Iterando esta idea, es evidente que el elemento ![]() de la matriz
de la matriz ![]() representa la probabilidad
representa la probabilidad ![]() . Por ejemplo,
. Por ejemplo,
![Rendered by QuickLaTeX.com \[P^{32} =\begin{matrix} \begin{matrix} \:\:A \quad& \:\:B\quad & \:\:C \quad& \:\:D\quad &\:\: E \quad\end{matrix} & \\ \left(\ \ \begin{matrix} 0.293 & 0.293 & 0.293 & 0.293 & 0.293 \\ 0.390 & 0.390 & 0.390 & 0.390 & 0.390 \\ 0.220 & 0.220 & 0.220 & 0.220 & 0.220 \\ 0.024 & 0.024 & 0.024 & 0.024 & 0.024 \\ 0.073 & 0.073 & 0.073 & 0.073 & 0.073 \end{matrix} \ \ \right) & \begin{matrix} A \\ B\\ C\\ D\\ E\end{matrix}\end{matrix}\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-c21f9e069949f27b8aabffef3fbfedec_l3.png)
Notar que todas las columnas de ![]() son idénticas si trabajamos con 3 decimales de precisión y, además, son iguales a las columnas de
son idénticas si trabajamos con 3 decimales de precisión y, además, son iguales a las columnas de ![]() cuando
cuando ![]() . Si elegimos mayor precisión, también encontraremos esta estabilidad, pero para un exponente
. Si elegimos mayor precisión, también encontraremos esta estabilidad, pero para un exponente ![]() mayor que
mayor que ![]() . Por tanto, después de
. Por tanto, después de ![]() pasos, para
pasos, para ![]() suficientemente grande, ¡la probabilidad de estar en una determinada página no depende de la página en la que comenzamos!
suficientemente grande, ¡la probabilidad de estar en una determinada página no depende de la página en la que comenzamos!
Más aún, si consideramos el vector
![]()
(aquí ![]() es un vector vertical, luego su traspuesto
es un vector vertical, luego su traspuesto ![]() es un vector horizontal, se comprueba fácilmente que
es un vector horizontal, se comprueba fácilmente que ![]() . Si la
. Si la ![]() -ésima coordenada de del vector
-ésima coordenada de del vector ![]() representa la probabilidad de estar en la página
representa la probabilidad de estar en la página ![]() en un determinado momento
en un determinado momento ![]() y, por tanto,
y, por tanto, ![]() representa la distribución de probabilidad de las páginas en ese momento
representa la distribución de probabilidad de las páginas en ese momento ![]() , entonces
, entonces ![]() también representa la distribución de probabilidad en el momento
también representa la distribución de probabilidad en el momento ![]() . Por esta razón, el vector
. Por esta razón, el vector ![]() se dice distribución estacionaria. Esta distribución estacionaria permite la ordenación de las páginas. En nuestro ejemplo, ordenamos las páginas de la siguiente manera:
se dice distribución estacionaria. Esta distribución estacionaria permite la ordenación de las páginas. En nuestro ejemplo, ordenamos las páginas de la siguiente manera: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , declarando que
, declarando que ![]() es la página más importante.
es la página más importante.
El caso general
El caso general puede ser puede ser abordado de la misma manera que nuestro ejemplo. Representamos la red como un grafo orientado en el cual los ![]() vértices representan las
vértices representan las ![]() páginas de la red y las aristas orientadas representan enlaces entre páginas. Trasladamos la información del grafo a una matriz
páginas de la red y las aristas orientadas representan enlaces entre páginas. Trasladamos la información del grafo a una matriz ![]() de tamaño
de tamaño ![]() , donde la
, donde la ![]() -ésima columna representa la
-ésima columna representa la ![]() -ésima página de partida y la
-ésima página de partida y la ![]() -ésima fila representa la
-ésima fila representa la ![]() -ésima página de destino. En nuestro ejemplo encontramos un vector
-ésima página de destino. En nuestro ejemplo encontramos un vector ![]() que cumple que
que cumple que ![]() . Este vector es, por tanto, un vector propio de valor propio
. Este vector es, por tanto, un vector propio de valor propio ![]() . Recordamos en este punto las definiciones de vector propio y valor propio.
. Recordamos en este punto las definiciones de vector propio y valor propio.
Definición. Sea ![]() una matriz de tamaño
una matriz de tamaño ![]() . Un número
. Un número ![]() se dice valor propio de
se dice valor propio de ![]() si existe un vector no nulo
si existe un vector no nulo ![]() tal que
tal que ![]() . Tal vector
. Tal vector ![]() se dice vector propio de
se dice vector propio de ![]() .
.
Recordamos también el método para encontrar valores y vectores propios.
Proposición Sea ![]() una matriz de tamaño
una matriz de tamaño ![]() . Los valores propios de
. Los valores propios de ![]() son las raíces polinomio característico
son las raíces polinomio característico ![]() , donde
, donde ![]() es la matriz identidad de tamaño
es la matriz identidad de tamaño ![]() . Los vectores propios asociados al valor propio
. Los vectores propios asociados al valor propio ![]() son las soluciones no nulas del sistema lineal homogéneo
son las soluciones no nulas del sistema lineal homogéneo ![]() .
.
El siguiente teorema debido a Frobenius garantiza que la matriz asociada al grafo de una red siempre tiene una solución estacionaria.
Teorema (Teorema de Frobenius) Sea ![]() la matriz de transición de un proceso de cadena de Markov de tamaño
la matriz de transición de un proceso de cadena de Markov de tamaño ![]() Markov (esto es,
Markov (esto es, ![]() para cualesquiera
para cualesquiera ![]() y la suma de las componentes de cada columna es igual a
y la suma de las componentes de cada columna es igual a ![]() :
: ![]() ). Se tiene que
). Se tiene que
-
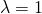 es valor propio de
es valor propio de 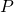 .
.
- Cualquier valor propio
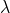 de
de 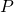 verifica
verifica  .
.
- Existe un vector propio
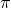 de valor propio
de valor propio 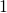 , cuyas coordenadas son todas mayores o iguales que cero. Sin pérdida de generalidad, podemos asumir que la suma de sus coordenadas es
, cuyas coordenadas son todas mayores o iguales que cero. Sin pérdida de generalidad, podemos asumir que la suma de sus coordenadas es 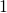 .
.
Ahora es el momento de admirar la potencia de este teorema. Para ello, consideramos la siguiente hipótesis simplificada: suponemos que la matriz ![]() tiene una base formada por vectores propios
tiene una base formada por vectores propios ![]() y que
y que ![]() es el vector
es el vector ![]() del teorema de Frobenius. Se tiene que para cada
del teorema de Frobenius. Se tiene que para cada ![]() existe
existe ![]() tal que
tal que ![]() . Sean
. Sean ![]() un vector no nulo y
un vector no nulo y ![]() , donde
, donde ![]() y
y ![]() . Descomponemos
. Descomponemos ![]() con respecto a la base
con respecto a la base ![]() :
:
![Rendered by QuickLaTeX.com \[X=\sum_{i=1}^N a_iv_i.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-75c52ea84c4a0aa148f3aa2977bdb8be_l3.png)
Una demostración técnica que omitimos aquí prueba que ![]() . Ahora calculamos
. Ahora calculamos ![]() :
:
![Rendered by QuickLaTeX.com \[PX= \sum_{i=1}^Na_i Pv_i= \sum_{i=1}^n a_i\lambda_iv_i,\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-3f5f58d838bdce8623400f20b0c3eb55_l3.png)
ya que ![]() es un vector propio de valor propio
es un vector propio de valor propio ![]() . Iterando, se obtiene que
. Iterando, se obtiene que
![Rendered by QuickLaTeX.com \[P^nX= \sum_{i=1}^n a_i\lambda_i^nv_i.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-42c385cba649519613da2a81cae3b1bb_l3.png)
Si todos los valores ![]() para
para ![]() verifican
verifican ![]() , entonces
, entonces
![]()
¡Esto es exactamente lo que sucede en nuestro ejemplo!
Sin embargo, conviene notar que el teorema no garantiza que cualquier matriz ![]() que verifique las hipótesis tiene esta propiedad. Describamos entonces los posibles casos patológicos y sus remedios.
que verifique las hipótesis tiene esta propiedad. Describamos entonces los posibles casos patológicos y sus remedios.
Posibles casos patológicos.
- El valor propio
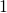 puede ser una raíz múltiple del polinomio característico
puede ser una raíz múltiple del polinomio característico  .
.
- La matriz
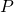 puede tener otros valores propios
puede tener otros valores propios 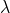 distintos
distintos 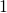 de módulo
de módulo 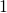 .
.
¿Qué podemos hacer en estos casos?
Decimos que una matriz de transición de Markov que no tiene patologías es una
matriz de transición de Markov regular, esto es:
Definición. Una matriz de transición de Markov se dice regular si
- El valor propio
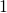 es una raíz simple del polinomio característico
es una raíz simple del polinomio característico  .
.
- Todos los valores propios
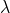 de
de 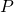 distintos de
distintos de 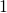 tienen módulo estrictamente menor que
tienen módulo estrictamente menor que 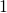 .
.
Notar que la mayoría de las matrices ![]() son regulares. Por tanto, si la matriz de transición de Markov de una red no es regular, la estrategia a seguir es deformarla ligeramente hasta conseguir una matriz regular.
son regulares. Por tanto, si la matriz de transición de Markov de una red no es regular, la estrategia a seguir es deformarla ligeramente hasta conseguir una matriz regular.
Remedio.
Consideramos la matriz ![]() de tamaño
de tamaño ![]() con
con ![]() para cualesquiera
para cualesquiera ![]() . Remplazamos la matriz
. Remplazamos la matriz ![]() asociada a la red por la matriz
asociada a la red por la matriz
(1) ![]()
para un valor pequeño de ![]() (el valor
(el valor ![]() es el usado por Google). Notar que todos los elementos de la matriz
es el usado por Google). Notar que todos los elementos de la matriz ![]() siguen siendo no negativos y que la suma de los elementos de cada columna es
siguen siendo no negativos y que la suma de los elementos de cada columna es ![]() , luego es una matriz de transición de Markov. El siguiente teorema garantiza que existe tal valor
, luego es una matriz de transición de Markov. El siguiente teorema garantiza que existe tal valor ![]() que remedia esta patología.
que remedia esta patología.
Teorema Dada una matriz de transición de Markov ![]() existe
existe ![]() positivo, tan pequeño como se quiera, tal que la matriz
positivo, tan pequeño como se quiera, tal que la matriz ![]() es regular. Sea
es regular. Sea ![]() el vector propio de valor propio
el vector propio de valor propio ![]() para la matriz
para la matriz ![]() , normalizado de manera que la suma de sus coordenadas es
, normalizado de manera que la suma de sus coordenadas es ![]() . Dado un vector no nulo
. Dado un vector no nulo ![]() con
con ![]() , donde
, donde ![]() y
y ![]() , se tiene que
, se tiene que
(2) ![]()
Relación con el teorema del punto fijo de Banach
En otra viñeta se trata el teorema del punto fijo de Banach, del que el teorema anterior puede ser visto como una aplicación particular. De hecho, se tiene que
Teorema
Sea ![]() una matriz de transición de Markov regular. Consideramos
una matriz de transición de Markov regular. Consideramos
![]() ,
,
con una cierta distancia ![]() entre puntos (que depende de
entre puntos (que depende de ![]() ). Sea el operador lineal
). Sea el operador lineal ![]() definido en
definido en ![]() por
por ![]() .
.
Se tiene que el operador ![]() es una contracción en
es una contracción en ![]() , esto es, existe
, esto es, existe ![]() tal que para cualesquiera
tal que para cualesquiera ![]() se cumple que
se cumple que
![]()
Además, existe un único vector ![]() tal que
tal que ![]() y dado cualquier
y dado cualquier ![]() , se puede definir por inducción la secuencia
, se puede definir por inducción la secuencia ![]() , donde
, donde ![]() , y se cumple que
, y se cumple que ![]() .
.
Definición of la distancia ![]() .
.
La definición de la distancia ![]() es un tanto sutil y puede ser omitida. Se incluye aquí por completitud, para el lector que desee insistir en los detalles. Nos limitamos al caso en que la matriz
es un tanto sutil y puede ser omitida. Se incluye aquí por completitud, para el lector que desee insistir en los detalles. Nos limitamos al caso en que la matriz ![]() es diagonalizable. Sea
es diagonalizable. Sea ![]() una base de vectores propios. Cualesquiera vectores
una base de vectores propios. Cualesquiera vectores ![]() pueden expresarse en la base
pueden expresarse en la base ![]() :
:
![Rendered by QuickLaTeX.com \[X=\sum_{i=1}^N a_iv_i, \quad Y=\sum_{i=1}^N b_iv_i,\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-e4878c51bc88f673f3e86656255bb8ef_l3.png)
donde ![]() . Definimos entonces
. Definimos entonces
![Rendered by QuickLaTeX.com \[d(X,Y)=\sum_{i=1}^n |a_i-b_i|.\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-ca97409e4ea4eb245c8b0400d97b8332_l3.png)
Con esta definición de distancia ![]() es un espacio métrico completo, es decir, toda sucesión de Cauchy es convergente.
es un espacio métrico completo, es decir, toda sucesión de Cauchy es convergente.
Este teorema no solo garantiza la existencia de ![]() , sino que da un método para construirlo como límite de la secuencia
, sino que da un método para construirlo como límite de la secuencia ![]() . Nuestro sencillo ejemplo ilustra esta convergencia. De hecho, la
. Nuestro sencillo ejemplo ilustra esta convergencia. De hecho, la ![]() -ésima columna de
-ésima columna de ![]() es el vector
es el vector ![]() , donde
, donde ![]() es el
es el ![]() -ésimo vector de la base canónica. Por supuesto, en nuestro ejemplo podríamos haber hallado directamente el vector
-ésimo vector de la base canónica. Por supuesto, en nuestro ejemplo podríamos haber hallado directamente el vector ![]() resolviendo el sistema
resolviendo el sistema ![]() que tiene como matriz de coeficientes
que tiene como matriz de coeficientes
![Rendered by QuickLaTeX.com \[I-P= \left(\begin{matrix} 1 &- \frac12 & -\frac13 & -1 & 0 \\ -1 & 1 & -\frac13 & 0 & -\frac13 \\ 0 & -\frac12 & 1 & 0 & -\frac13 \\ 0 & 0 & 0 & 1 & -\frac13 \\ 0 & 0 & -\frac13 & 0 & 1 \end{matrix}\right).\]](https://blog.kleinproject.org/wp-content/ql-cache/quicklatex.com-f5e410a0661ff0ac5833a68bd5741a11_l3.png)
Las soluciones de este sistema son todas de la forma ![]() para
para ![]() . Por tanto, la solución cuya suma de coordenadas es igual a
. Por tanto, la solución cuya suma de coordenadas es igual a ![]() es
es ![]() , donde
, donde
![]()
Cálculo en la práctica de la distribución estacionaria
Hemos identificado la sencilla idea que subyace en el algoritmo. Sin embargo, encontrar la distribución estacionaria ![]() (esto es, un vector propio de valor propio
(esto es, un vector propio de valor propio ![]() para la matriz
para la matriz ![]() en (1)) no es una tarea sencilla cuando la matriz tiene miles de millones de filas y columnas: el tiempo de computación y la memoria física que se requiere para ello representan verdaderos desafíos. El habitual método de eliminación de Gauss no es útil en este caso por el tamaño de los cálculos y porque se requiere dividir por coeficientes pequeños. Un algoritmo más eficiente hace uso de la propiedad (2) de estas matrices (ver [LM]). Este es el vínculo con la viñeta acerca del teorema del punto fijo de Banach, en la que se verá que la demostración del dicho teorema proporciona un algoritmo para construir el punto fijo.
en (1)) no es una tarea sencilla cuando la matriz tiene miles de millones de filas y columnas: el tiempo de computación y la memoria física que se requiere para ello representan verdaderos desafíos. El habitual método de eliminación de Gauss no es útil en este caso por el tamaño de los cálculos y porque se requiere dividir por coeficientes pequeños. Un algoritmo más eficiente hace uso de la propiedad (2) de estas matrices (ver [LM]). Este es el vínculo con la viñeta acerca del teorema del punto fijo de Banach, en la que se verá que la demostración del dicho teorema proporciona un algoritmo para construir el punto fijo.
De hecho, se parte de un ![]() tal que
tal que
![]()
y se necesita calcular ![]() . Habitualmente
. Habitualmente ![]() para
para ![]() entre
entre ![]() y
y ![]() da una aproximación de
da una aproximación de ![]() bastante buena. Por inducción, se obtiene
bastante buena. Por inducción, se obtiene ![]() , pero incluso estos cálculos resultan largos. De hecho, debido a su construcción, la matriz
, pero incluso estos cálculos resultan largos. De hecho, debido a su construcción, la matriz ![]() en (1) no tiene elementos no nulos, mientras que la mayoría de los elementos de la matriz
en (1) no tiene elementos no nulos, mientras que la mayoría de los elementos de la matriz ![]() son cero, algo que debemos aprovechar:
son cero, algo que debemos aprovechar:
![]()
Debido a la especial forma de ![]() , es fácil comprobar que si
, es fácil comprobar que si ![]() es un vector cuyas coordenadas suman
es un vector cuyas coordenadas suman ![]() entonces
entonces ![]() . Por tanto, es suficiente con calcular la secuencia
. Por tanto, es suficiente con calcular la secuencia
![]()
Conclusión
En esta viñeta se ha presentado la parte pública del algoritmo PageRank de Google. Ahora el lector puede experimentar con redes sencillas y encontrar trucos para mejorar la posición de su página personal añadiendo enlaces tanto internos como externos de manera adecuada. Algunas de las partes privadas más sofisticadas continúan aún en desarrollo. Algunas de ellas consisten en remplazar la matriz «neutra» ![]() en (1) por otras matrices que reflejen los gustos del navegante en la red. Otras se aseguran de que el orden de las páginas no sea demasiado sensible a las manipulaciones de aquellos que intentan mejorar la posición de sus páginas.
en (1) por otras matrices que reflejen los gustos del navegante en la red. Otras se aseguran de que el orden de las páginas no sea demasiado sensible a las manipulaciones de aquellos que intentan mejorar la posición de sus páginas.
Como conclusión general, ¿qué hemos observado? Que una idea simple e ingeniosa ha dado lugar a un enorme progreso en la eficiencia de los motores de búsqueda y al nacimiento de un verdadero imperio comercial.
Si bien la implementación es en sí una hazaña computacional, la idea inicial requiere matemáticas «elementales»: álgebra lineal y teoría de probabilidades. Las herramientas utilizadas, especialmente la diagonalización de matrices, son estándar en matemáticas pero han demostrado su verdadera potencia cuando se han usado fuera de su contexto «habitual». También hemos incidido en las ideas unificadoras dentro de la ciencia cuando hemos considerado el teorema del punto fijo de Banach y sus aplicaciones a situaciones tan alejadas de su origen.
Bibliografía
[E] M. Eisermann, Comment Google classe les pages webb,
http://images.math.cnrs.fr/Comment-Google-classe-les-pages.html, 2009.
[LM] A. N. Langville and C. D. Meyer, A Survey of Eigenvector Methods
for Web Information Retrieval, SIAM Review, Volume 47, Issue 1,
(2005), pp. 135–161.
[RS] C. Rousseau and Y. Saint-Aubin, Mathematics and
technology, SUMAT Series, Springer-Verlag, 2008 (A French version of the book exists, published in the same series.)
